中厚圆柱壳振型的有限元超收敛拼片恢复解和网格自适应分析
2021-10-11王永亮
王永亮
(1.中国矿业大学(北京) 力学与建筑工程学院,北京 100083;2.中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室,北京 100083)
结构和弹性体的动力分析是结构抗震、岩体诱发地震研究的重要基础[1-2],作为支撑结构或储藏腔体的圆柱壳在结构工程、岩体工程、航空航天工程中广泛应用,研究该结构的振动、失稳、屈曲等动力特性对于研判其失效行为具有重要意义[3-4]。目前研究壳体问题常采用传统的薄壳理论[5-8],该理论基于Kirchhoff-Love假定、忽略横向剪切变形[9],对于具有较小剪切刚度(即容易发生显著横向剪切变形)的壳体结构将引入一定误差[10-11]。另外,实际工程中板壳结构壁厚的增加往往超出薄壁理论的应用范围,也要求考虑横向剪切变形的影响。中厚壳自由振动理论相比薄壳自由振动理论,考虑了横向剪切变形和转动惯量的影响,使解答更加可靠。
复杂结构形式和边界条件的中厚圆柱壳自由振动分析多采用有限元法进行求解,高精度自振频率和振型的数值解也成为结构精准损伤识别的关键基础[12-13]。相比常规有限元法,自适应有限元法可获得满足用户指定误差限的高精度解答[14],自适应算法成为优化网格、提高解答精度的重要方法[15-17],主要包括提高单元阶次的p型自适应方法[18]、增加网格密度的h型自适应方法[19]、以及二者结合的ph型自适应方法[20]等。自适应有限元法在梁、板、壳自由振动和弹性稳定等结构特征值问题的高精度求解中显示出良好潜力[21-23]。本文研究中厚圆柱壳的自由振动问题,该问题为典型的二阶常微分方程组特征值问题;对于各类边界条件、不同环向波数和厚长比中厚圆柱壳的连续阶频率和振型求解,成为挑战常微分方程组特征值问题求解的难点。针对上述问题,本文将推广前期建立的变截面Euler-Bernoulli梁自由振动分析的自适应算法,合理引入位移超收敛拼片恢复方法和高阶形函数插值技术、能量模误差估计技术、网格细分加密方法,形成一套中厚圆柱壳自由振动分析的h型有限元自适应求解方案。经数值算例检验,该方法展示出良好的求解效力,本文旨在报道这些新进展和成果。
1 振动方程
考虑图1所示的中厚圆柱壳,ox为旋转轴,建立中面上A点的局部坐标系αβγ,其中α沿子午线切向方向、β沿纬圆切向方向、γ沿法线方向。中厚圆柱壳振动的5个独立位移为:沿α方向的线位移u、沿β方向的线位移v、沿γ方向的线位移w、绕α的转角位移ϕ、绕β的转角位移ψ。记圆柱壳中面半径为r,截面厚度为h,截面剪切刚度修正系数为κ,惯性矩为J,长度为l;材料弹性模量为E,剪切模量为G,Poisson比为μ,密度为ρ。

图1 中厚圆柱壳坐标系和符号Fig.1 Coordinate systems and symbols of moderately thick circular cylindrical shell
本文研究的中厚圆柱壳自由振动的微分控制方程为
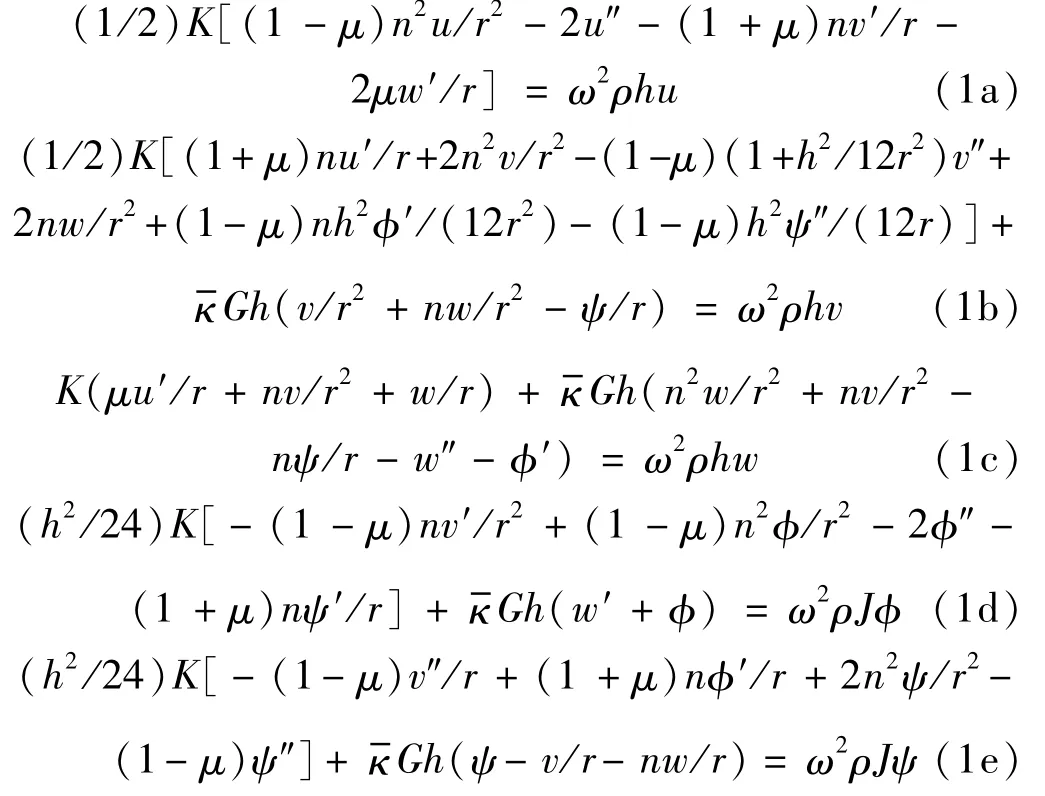
式中:()′=d()/d x;ω为自振频率;n为环向振型的波数;其余参数参见文献[24]。
上述二阶常微分方程组特征值问题,可表示为如下矩阵形式

式中:L,R为相应的微分算子矩阵;u={u,v,w,ϕ,ψ}T={u1,u2,u3,u4,u5}T为振型(位移)函数向量;ω,u分别对应于特征值和特征向量,本文亦将(ω,u)合称为特征对。
2 自适应目标和步骤
设要求解中厚圆柱壳自由振动问题式(2)的某阶特征对(ω,u),本文的中厚圆柱壳自由振动自适应求解目标为:在精确解(ω,u)未知的情况下,事先给定误差限Tol,寻求一个优化的有限元网格π,使该网格上的有限元解(ωh,uh)同时满足

实施时,由于精确解(ω,u)事先未知,上述目标不能作为停机准则。对于振型,由于下文介绍的振型(位移)超收敛拼片恢复解u*较uh具有更高的收敛阶,即u*比uh更接近精确解u,因此采用u*代替u对uh进行误差估计和控制,形成能量模形式的误差估计;对于频率,利用位移超收敛解计算Rayleigh商[25]得到频率的超收敛解。通过Rayleigh商得出的频率超收敛解比振型超收敛解具有更高的收敛阶,本文通过估计和控制振型解答的误差可保证频率解答满足误差要求,如此形成本方法通过控制振型误差的停机准则。基于有限元解的误差估计进行网格细分加密,即可求得优化的网格和满足误差限的各阶高精度频率和振型解答,形成一套h型有限元自适应方案。自适应求解步骤包括:
步骤1有限元解——在当前网格上(初始网格由用户提供),进行常规有限元计算,得到当前网格下的有限元解(ωh,uh);
步骤2误差估计——利用有限元后处理超收敛算法,可得当前网格下频率和振型的超收敛解(ω*,u*);同时,可得超收敛解与有限元解之间的误差估计值;
步骤3网格细分——对于误差估计不满足误差限的单元,用网格细分加密方法将其细分,得到新的有限元网格,返回步骤1;如果所有单元均满足误差限,则网格无需再细分,求解过程结束。
3 有限元解
对于求解中厚圆柱壳自由振动问题式(2),在给定有限元网格π下,常规有限元将建立如下线性矩阵特征值问题

式中:D为振型向量;K和M为静力刚度矩阵和一致质量矩阵。在当前网格下求解可得有限元解(ωh,uh),需要指出的是,该解答的精度与网格相关,高精度的解答需要高质量的有限元网格。
4 误差估计
有限元位移解在单元内部具有hm+1阶的超收敛性,在单元节点上具有h2m阶的超收敛性,这些节点成为位移超收敛点。超收敛点上解答的误差比其他区域解答更小,具有更快的收敛速度。通过多个相邻单元进行连接拼片,利用拼片上位于多个超收敛点的超收敛解和次高阶形函数(高于当前形函数阶次m,即≥m+1)插值,即可恢复获得拼片单元上的超收敛解,形成位移超收敛拼片恢复方法[26-27]。本文对于中厚圆柱壳的自由振动问题,求得振型(位移)的有限元解后,同样可以获得各阶振型的超收敛解。通过将单元e的相邻单元进行组合拼片,拼片单元的位移超收敛解的插值形式为

式中:P为给定函数向量;a为待定系数向量。

系数a的取值通过求得如下泛函的极小值使式(6)中乘积结果在单元节点处等于当前节点位移值来确定

式中,n为进行拼片单元的节点数目。
使用最小二乘法求解式(8),即可获得系数a的值

式中:各系数矩阵为
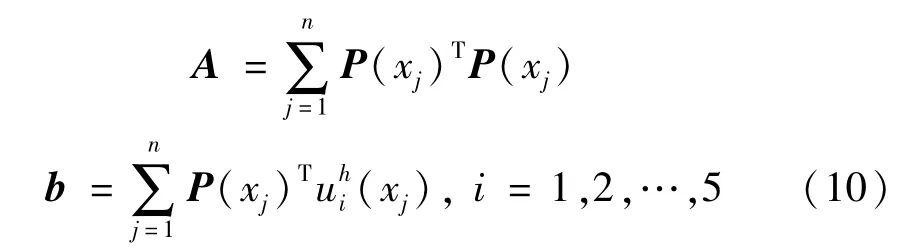
确定a后,即可通过式(6)得到拼片单元的位移超收敛解,该超收敛解具有比当前网格下有限元解更高的收敛阶,可用于估计有限元解的误差。
使用获得的位移超收敛解,并通过如下Rayleigh商的计算,可以得到频率的超收敛解ω*

式中,a(),b()为应变能、动能内积。利用当前网格下位移超收敛解和有限元解,可得能量模形式下的误差估计[28]
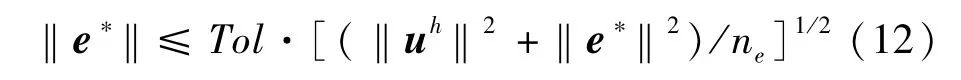
式中:ne为进行拼片的单元数目;e*为位移超收敛解u*和有限元解uh的误差,并有能量范数表达式
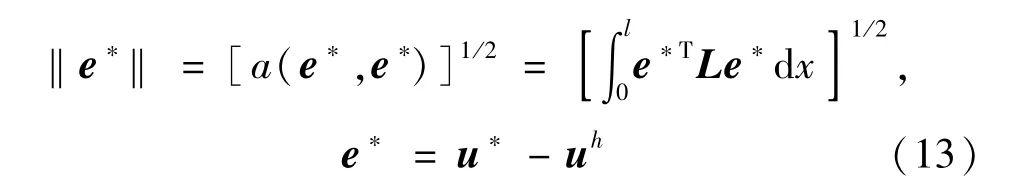
进一步,式(12)可写为
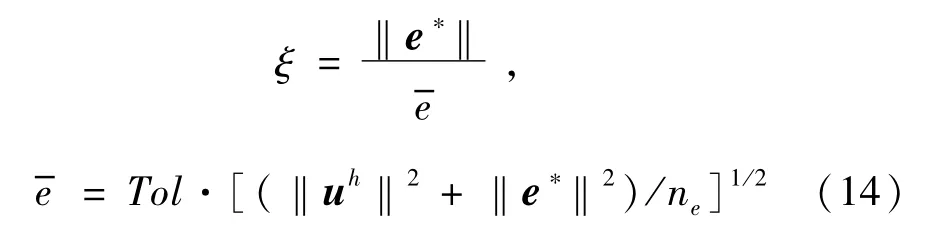
式中,ξ为相对误差,该值应满足

这里需要指出,通过Rayleigh商计算得到的频率超收敛解比振型超收敛解具有更高的收敛阶,针对振型进行误差估计和控制,即可获得高精度的振型并确保频率的准确性。
5 网格细分加密
如果当前单元e上误差估计式(15)不满足,表明该单元需要进行细分加密来降低解答误差。本文采用将当前单元均匀细分形成多个单元的网格细分加密方式,新单元的长度与当前单元上的误差和单元阶次相关,估计式为

式中:hnew为新单元长度;hold当前单元e的长度。为使自适应计算更加高效、避免网格冗余,本文对每次单元细分加密数目进行控制,实施方案为
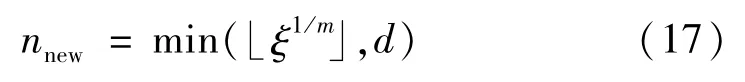
式中:nnew为网格细分后新单元数目;d为单元细分的极限数目;⎿·」为向下取整符号。
经过以上有限元解的误差估计和网格细分加密,最终可以得到优化的网格,并获得该优化网格上满足误差限的各阶高精度频率和振型解答。
6 数值算例
本文算法已经编制成Fortran 90程序,本章给出使用本文方法求解多种中厚圆柱壳自由振动的数值算例,通过对比典型的中厚壳、薄壳结果来验证本文方法计算结果的精确性,并讨论求解不同环向波数、厚长比、边界条件下中厚圆柱壳自由振动问题的适用性。本节所有算例均采用3次元,初始网格采用2个单元,给定的初始误差限为Tol=10-4,设定单元细分的极限数目为d=6。文中k表示阶次,置于频率或振型符号的下标位置。
例1薄圆柱壳求解检验
考虑中厚圆柱壳在两端简支条件下的自由振动,圆柱壳基本参数为

采用本文方法求解不同环向波数(n=1~15)时的前2阶(k=1,2)特征对,表1所示为计算得到的频率结果。文献[29]、文献[30]采用中厚壳理论,分别利用混合有限元法和动力刚度法对该问题进行了求解,从表1可以看出本文结果与Sivadas等和陈旭东等的求解结果展示出良好的吻合性,检验了本文方法求解各阶频率的可靠性。
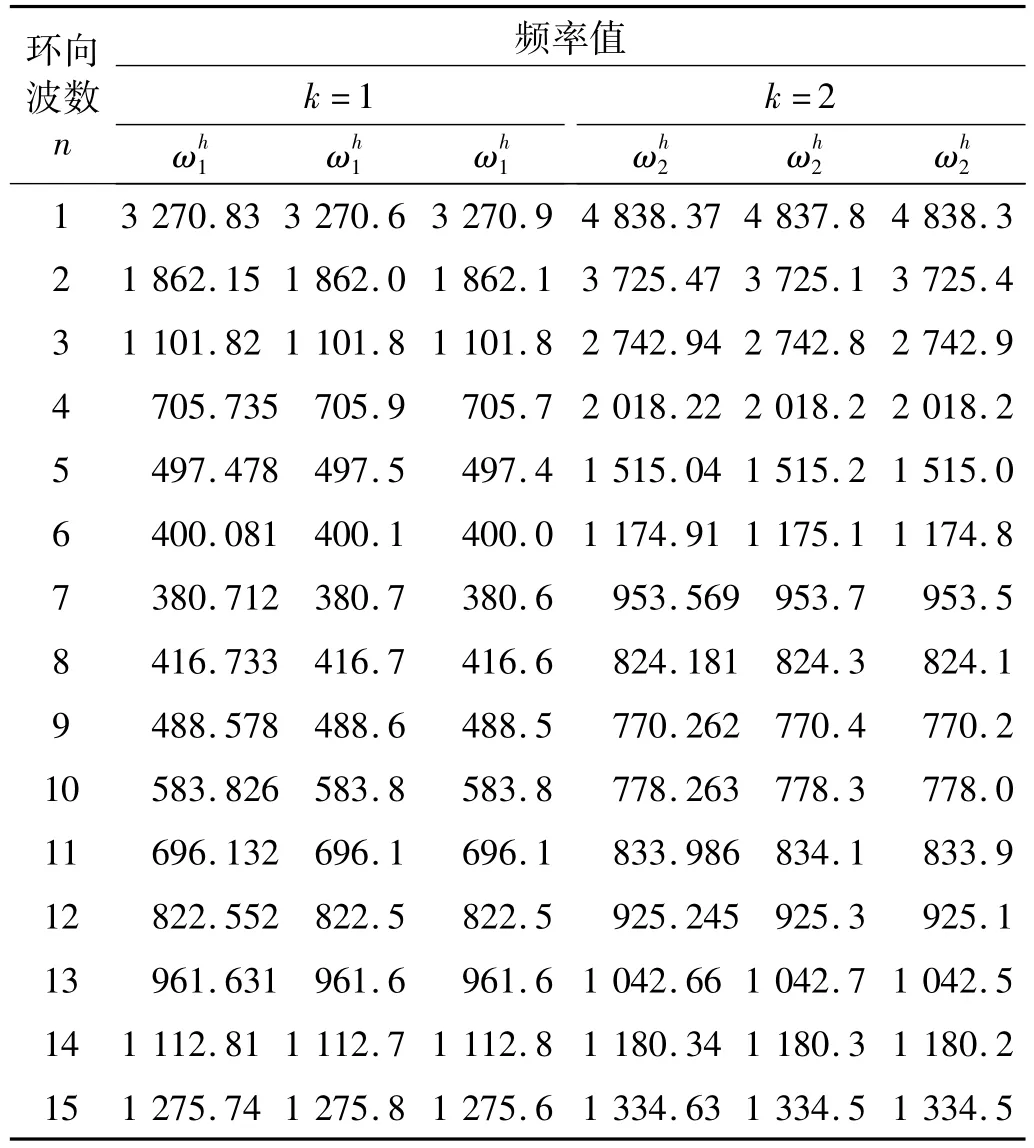
表1 中厚圆柱壳自由振动频率值ω/HzTab.1 Frequenciesω/Hz of moderately thick circular cylindrical shell
图2~图5列出了n=1和n=10的第1阶振型,并在横坐标轴上标出自适应求解的最终网格分布。需要说明的是,为方便直观显示和对比分析,本文中振型结果均进行归一化处理(令最大振型值为1),同时在振型图中也将横坐标轴进行归一化处理(令水平坐标轴为x/l)。从图2、图3可以看出,对于n=1时的第1阶振型在两端区域变化比较剧烈,自适应方法划分出相对比较细密的网格;振型在中间区域相对平缓,只需要使用稀疏的网格。
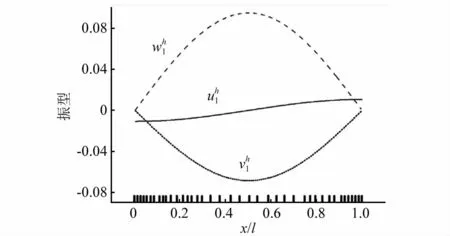
图2 n=1时,(,,)振型图和自适应网格Fig.2 Vibration mode(,,)and adaptive mesh with n=1
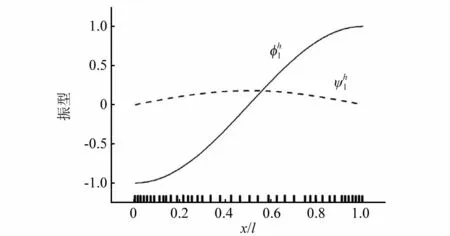
图3 n=1时,(,)振型图和自适应网格Fig.3 Vibration mode(,)and adaptive mesh with n=1
从图4、图5可以看出,对于n=10时的第1阶振型在两全域上变化比较平缓,自适应方法划分出相对稀疏、均匀的网格。有限元网格根据振型变化情况进行自适应加密优化,展示出良好适用性。
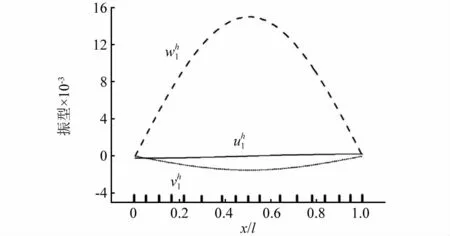
图4 n=10时,(,,)振型图和自适应网格Fig.4 Vibration mode(,,)and adaptive mesh with n=10

图5 n=10时,(,)振型图和自适应网格Fig.5 Vibration mode(,)and adaptive mesh with n=10
例2中厚圆柱壳连续阶频率求解
考虑中厚圆柱壳在两端简支条件下的自由振动,该圆柱壳基本参数为

使用本文方法计算了n=0情况下该圆柱壳自由振动的前15阶(k=1~15)连续特征对,将结果列于表2。文献[31]采用薄壳理论对本圆柱壳进行分析,研究中忽略该圆柱壳横向剪切变形,并使用动力刚度法对其进行了求解;文献[32]得到了相应的解析形式解答。
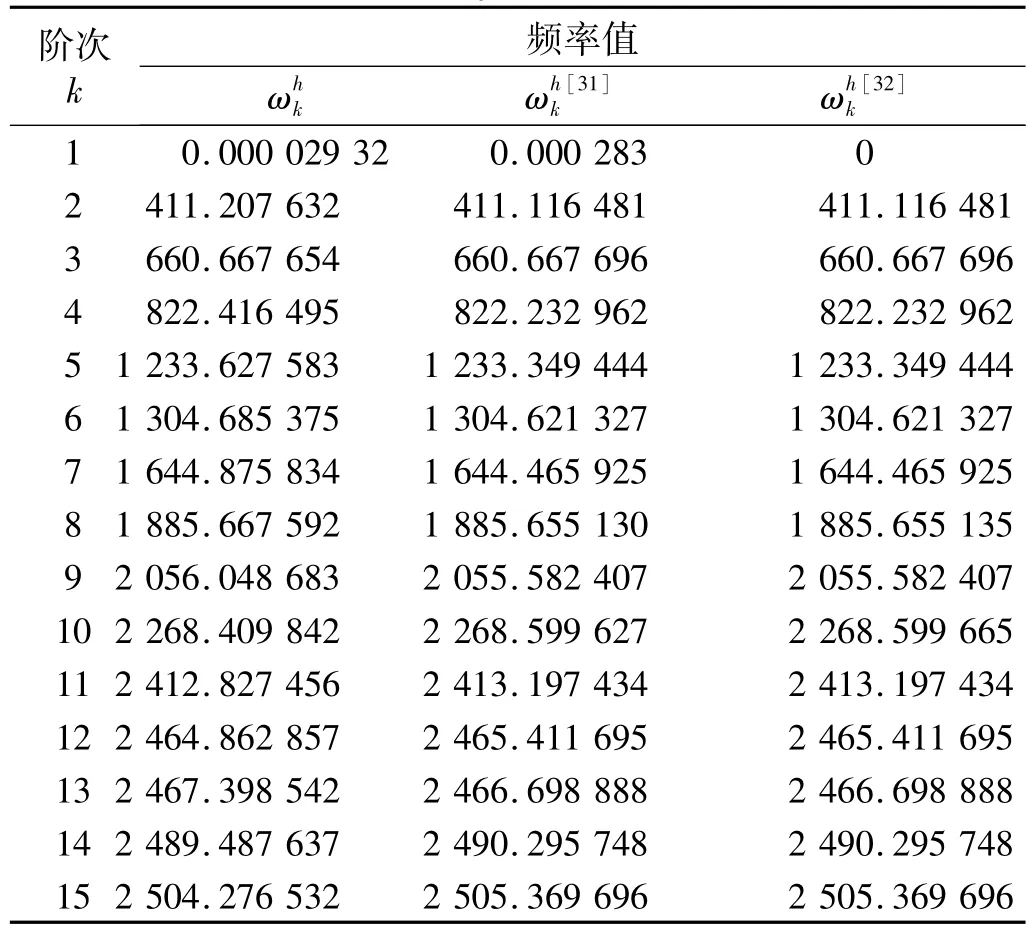
表2 中厚圆柱壳自由振动频率值ω/(rad·s-1)Tab.2 Frequenciesω/(rad·s-1)of moderately thick circular cylindrical shell
从表2可以看出本文结果与陈旭东和Leissa的求解结果在低阶时吻合很好,展示出本文自适应方法对圆柱壳连续阶次特求解的适用性;需要重点说明的是,随着阶次升高(如k=11~15),频率结果的差异愈加明显,这是由于采用薄壳理论对中厚圆柱壳结构进行分析引入的误差。
例3中厚圆柱壳不同环向波数n和厚长比h/l
下面分别考虑两端简支中厚圆柱壳在不同环向波数n、厚长比h/l条件下自由振动的求解。首先,考虑中厚圆柱壳在不同环向波数n(n=1~5)时的自由振动,设定圆柱壳Poisson比μ=0.3、长径比l/r=1.0、厚径比h/r=0.1,其余参数为

采用本文方法求解各种工况下的第1阶特征对,将自振频率结果转化为无量纲值列于表3,文献[33]采用沿圆柱壳周向位移分布形状函数的有限元模型、文献[34]采用层状圆柱壳模型对本算例求解并得到有效的解答,从表3可以看出的本文方法求得不同环向波数下中厚圆柱壳圆柱壳的结果与文献解答吻合性较好,展示出本文自适应方法对于各类环向波数圆柱壳体的适用性。
表3 中厚圆柱壳不同环向波数n自由振动无量纲频率值Tab.3 Non-dimensional frequencies of moderately thick circular cylindrical shell with different circumferential wave number n

表3 中厚圆柱壳不同环向波数n自由振动无量纲频率值Tab.3 Non-dimensional frequencies of moderately thick circular cylindrical shell with different circumferential wave number n
环向波数n频率值ω-h1 ω-h1[33] ω-h1[34]1 1.063 43 1.062 26 1.062 34 2 0.881 21 0.882 33 0.882 53 3 0.806 67 0.809 25 0.809 51 4 0.897 56 0.898 77 0.898 93 5 1.115 64 —1.122 09
同时,考虑中厚圆柱壳在不同厚长比h/l(h/l=0.01,h/l=0.10,h/l=0.20,h/l=0.40,h/l=0.60,h/l=0.80,h/l=1.00)工况下自由振动,设定圆柱壳环向波数n=0、径厚比h/r=0.4,采用本文方法求得了不同厚长h/l比下的第1阶(k=1)特征对,并将自振频率结果转化为无量纲值列于表4,可以看出本文结果与Armenakas等和Loy等求解的近似结果吻合较好,展示出本文自适应方法对于薄壁、厚壁等不同厚长比圆柱壳体的适用性。
表4 中厚圆柱壳不同厚长比h/l自由振动无量纲频率值Tab.4 Non-dimensional frequencies of moderately thick circular cylindrical shell with different ratio of thickness to length h/l

表4 中厚圆柱壳不同厚长比h/l自由振动无量纲频率值Tab.4 Non-dimensional frequencies of moderately thick circular cylindrical shell with different ratio of thickness to length h/l
厚长比h/l频率值ω-h1 ω-h1[33] ω-h1[34]0.01 0.016 11 0.016 12 0.010 02 0.10 0.152 91 0.152 89 0.100 00 0.20 0.203 76 0.204 95 0.200 00 0.40 0.278 54 0.275 40 0.275 44 0.60 0.422 12 0.420 22 0.420 35 0.80 0.597 75 0.600 09 0.600 33 1.00 0.784 32 0.792 74 0.793 14
例4中厚圆柱壳不同边界条件
为检验本文方法对不同边界条件分析的适用性,下面分别对两端简支、两端固定等典型边界条件的中厚圆柱壳自由振动进行求解。设中厚圆柱壳Poisson比μ=0.3、厚径比h/r=0.4,其余参数为

采用本文方法求解在两端简支、两端固定边界时圆柱壳环向波数n=0、不同厚长比h/l(h/l=0.1,h/l=0.2,h/l=0.4,h/l=0.6,h/l=0.8,h/l=1.0)工况下第2阶(k=2)特征对,将自振频率结果转化为无量纲值列于表5,可以看出本文结果与Loy等采用层状圆柱壳模型求解结果相吻合,展示出本文自适应方法对不同边界条件圆柱壳体分析的适用性。需要重点指出的是,本文自适应方法兼具通用性,误差估计和网格划分技术不依赖于边界条件,有潜力推广到工程实际问题中力边界、弹性边界、复合边界等复杂边界工况。
表5 中厚圆柱壳不同边界条件下自由振动无量纲频率值Tab.5 Non-dimensional frequencies of moderately thick circular cylindrical shell under different boundary conditions
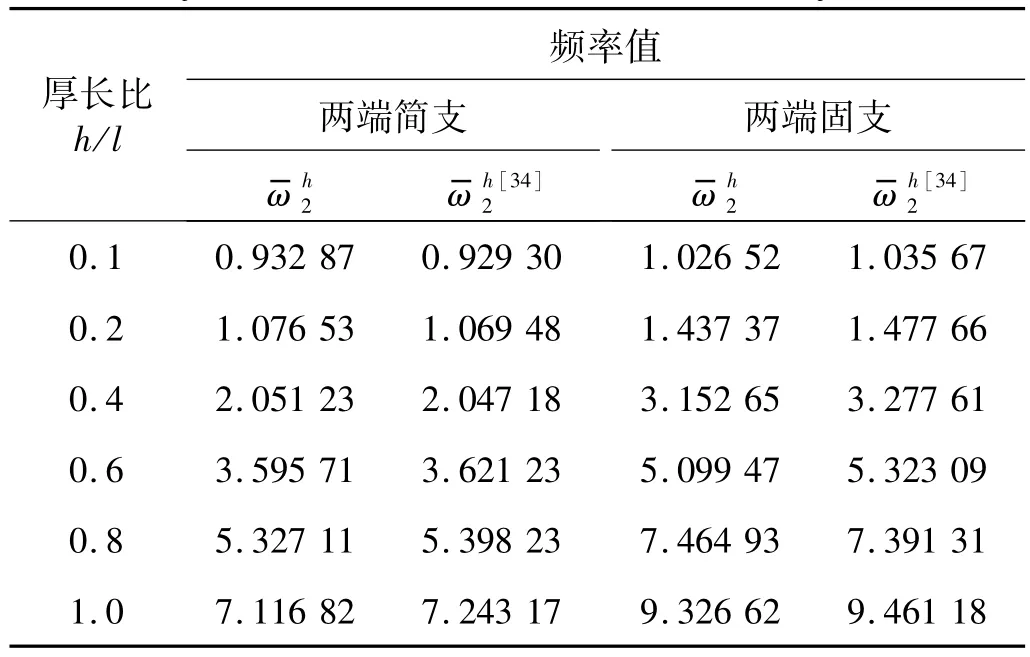
表5 中厚圆柱壳不同边界条件下自由振动无量纲频率值Tab.5 Non-dimensional frequencies of moderately thick circular cylindrical shell under different boundary conditions
厚长比h/l频率值两端简支ω-h2 ω-h2[34]两端固支ω-h2 ω-h2[34]0.1 0.932 87 0.929 30 1.026 52 1.035 67 0.2 1.076 53 1.069 48 1.437 37 1.477 66 0.4 2.051 23 2.047 18 3.152 65 3.277 61 0.6 3.595 71 3.621 23 5.099 47 5.323 09 0.8 5.327 11 5.398 23 7.464 93 7.391 31 1.0 7.116 82 7.243 17 9.326 62 9.461 18
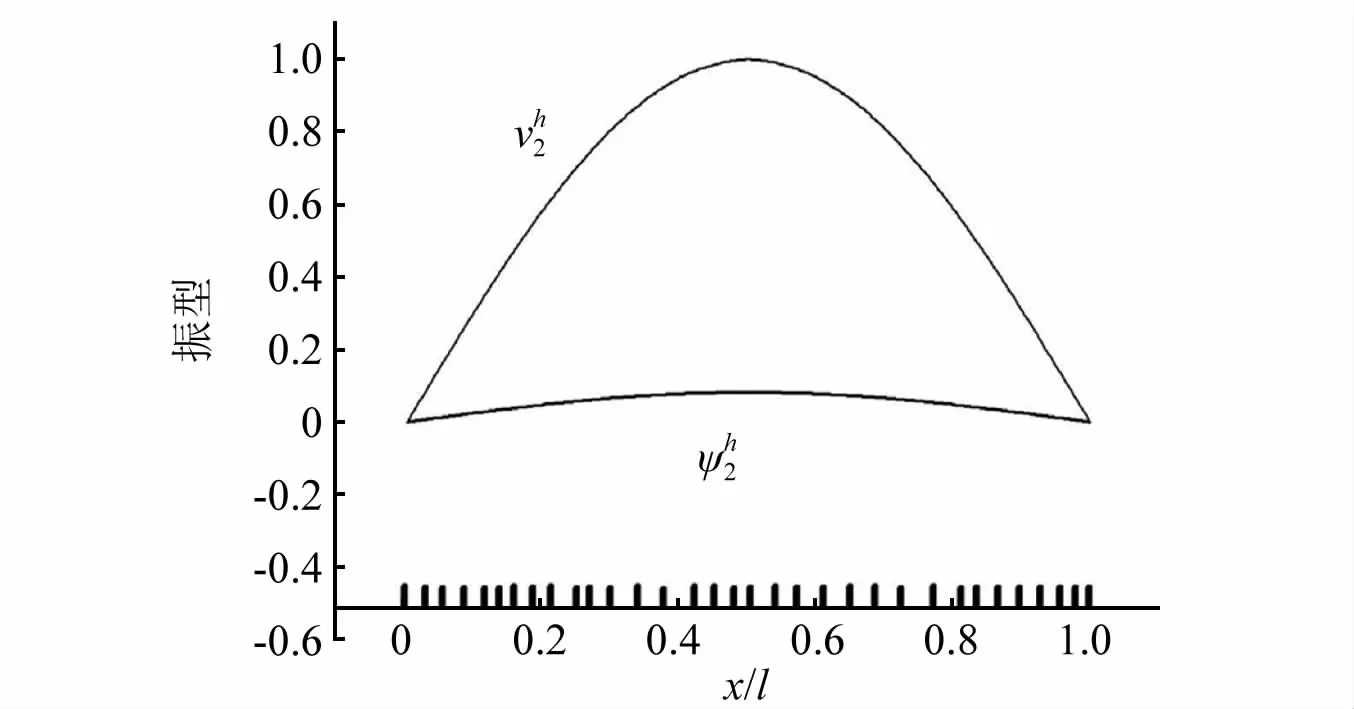
图6 两端简支边界条件下()振型图和自适应网格Fig.6 Vibration mode()and adaptive mesh under simply supported boundary conditions at both ends
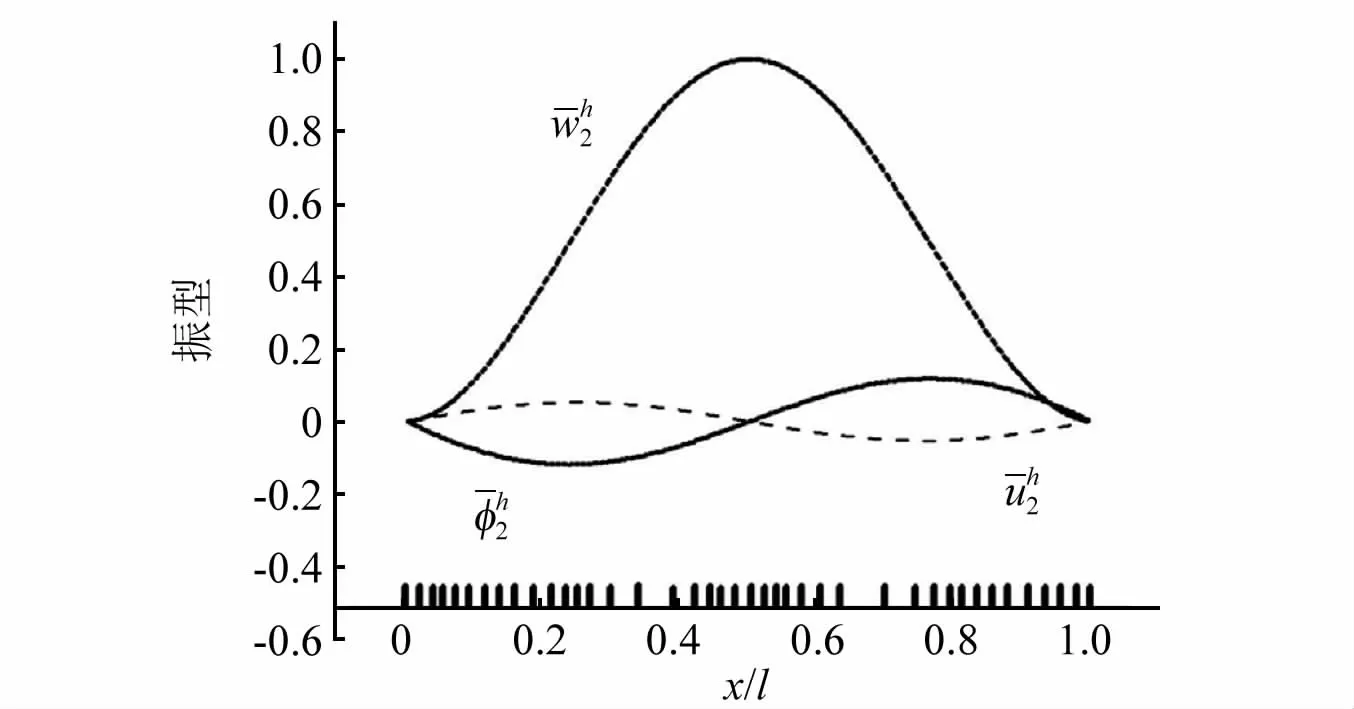
图7 两端固支边界条件下(,,)振型图和自适应网格Fig.7 Vibration mode(,,)and adaptive mesh under fixed boundary conditions at both ends
7 结 论
本文研究工作的主要结论和计算方法潜力可总结如下:
(1)本文建立了中厚圆柱壳振型的超收敛拼片恢复解,利用超收敛解估计当前网格下有限元解的误差,指导单元加密细分,形成非均匀分布的优化网格。在振型解答变化相对比较剧烈的区域,自适应方法可自动划分出相对细密的有限元网格,其他区域则使用相对稀疏网格。
(2)本文方法在中厚圆柱壳简支、固支等多类边界条件、不同环向波数和厚长比工况下连续阶的频率和振型求解中,均成功获得了优化的有限元网格和满足预设误差限的高精度解答,展示出良好的求解效力。
(3)本文方法兼具通用性,有潜力推广到一般结构特值问题振型(位移场)和固体应力(位移导数场)的精细化数值模型和高精度计算领域,成为下一阶段的研究内容。
