基于局部共振理论的齿轮成形磨削纵弯谐振系统设计

郭星晨，赵 波，尹 龙，别文博，王晓博

（河南理工大学 机械与动力工程学院，河南 焦作 454000）

大负载型成形砂轮盘谐振系统，为目前鲜有研究的齿轮成形磨削纵弯谐振振动系统。该系统分为两部分组成:圆锥过渡型复合变幅杆和成形砂轮盘。其中，变幅杆做单一纵向振动，激励成形砂轮做节圆型横向弯曲振动，从而实现两种不同振型的复合。在旋转超声加工领域，将振动附加在磨具上，通过改变材料去除机理，可降低宏观磨削力与磨削热，并具有精度高、效率高、成本低等优势[1-5]。由于盘形负载辐射面积大、功率大、带宽大等特点，故通常应用于超声清洗、超声换能器等声学领域，且相比超声钻削、铣削等，纵振变幅器具有较高的声辐射效率[6]。成形砂轮盘谐振系统作为齿轮超声磨削技术的关键，其设计理论对超声加工、超声后处理等应用具有重要影响。

据文献[7-8]显示，在多数超声振动系统设计中，若工具头满足两点条件之一，则可遵照全谐振设计理论进行设计，即变幅杆质量远大于工具杆，可忽略对系统设计的影响，亦或较大工具头可结合设计频率进行自由设计。文中所述砂轮作为变幅杆直接负载，其几何尺寸和相关材料特性等均取决于使用条件，故不能按照频率进行自由设计。再者，因其体积大、质量重，则全谐振设计方法不适用于本系统的设计。此外，全谐振设计方法是基于同一频率对系统整体进行设计，对系统各部分的精度要求较高，一般工装设计精度和加工条件难以满足所需要求，且少许偏差均可致使各部分谐振频率发生漂移，从而影响系统稳定性[9]。由此，局部共振设计方法为大负载工具头振动系统的设计提供了一种高效稳定的途径。

范国良等[10]最早在有关超声钻削深小孔加工中发现局部共振现象。随着超声加工技术的发展，基于局部共振理论，Lin等[11]和Suzuki等[12-13]分别提出整体共振设计和非谐振设计理论。李鹏涛等[14]运用局部共振理论设计了超声铣削声学系统。文献[15-17]基于Mindlin理论，对纵弯谐振变幅器及超声珩齿系统进行了一体式非谐振设计。文献[18-21]研究了变幅杆激励面积及变幅器几何尺寸，对矩形板和阶梯圆盘的谐振频率、振幅、振型等振动特性的影响规律。其中，局部共振理论既可使所需振动系统工具头几何尺寸根据使用条件进行设计，又可通过调节发生器频率，降低工具头因磨损所导致的谐振频率漂移影响，具有较高的稳定性。

基于以上研究，本文结合局部共振理论，对超声磨齿系统中的大负载成形砂轮盘纵弯谐振系统进行一体式设计。结合振动单元间的连续条件和边界条件，按照一体式设计思路建立纵弯谐振系统的理论模型和频率方程，并利用相关软件进行计算、建模及仿真模拟。此外，通过有限元模态分析、谐响应分析、阻抗分析试验和超声谐振试验，对系统频率以及实际效果进行分析验证，表明了基于局部共振设计理论的砂轮盘纵弯谐振系统设计方法的可行性与准确性。

1 齿轮成形磨削纵弯谐振系统理论模型

1.1 模型条件

基于局部共振耦合理论，本文采用一体式设计思路，对齿轮成形磨削砂轮盘振动系统进行设计。系统从左至右分为三段:圆柱段L1、圆锥过渡段L2以及砂轮盘段L3，λ为波长。 其中，R1=16 mm，R2=11 mm、变幅杆为3/4波长圆锥过渡型、设计频率为35.00 kHz、Ⅰ为磨齿工作端、Ⅱ为砂轮基体、Ⅲ为变幅杆、砂轮盘厚L3=12 mm。

齿轮成形磨削砂轮盘振动系统模型示意图，如图1所示。具体表现为:砂轮与变幅杆经螺母固连；为简化理论分析，忽略螺母的影响；换能器作为激励源与变幅杆经螺栓紧密连接。变幅杆中质点以纵波形式传向砂轮盘段，并转换为横波振动方式。鉴于砂轮厚度远小于其半径大小，故可将该段按薄圆盘振动形式处理。而当该系统做纵弯谐振时，砂轮盘单元则在纵振变幅杆的激励下做横向节圆型弯曲振动，即系统整体以纵-弯的形式传导。故，砂轮盘工作端质点实际振动方向表现为与变幅杆轴线形成一定夹角。

图1 齿轮成形磨削超声振动系统Fig.1 Gear forming and grinding ultrasonic vibration system

1.2 频率方程

谐振条件下，变截面杆纵振动波动方程表示为[22]

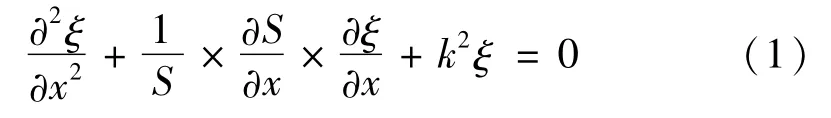
式中:S=S（x）为变幅杆的横截面积函数；ξ=ξ（x）为质点位移函数；k=ω/c，k为纵波圆波数，c为纵波在细棒中的传播速度，m/s。

结合式（1）求得变幅杆各段位移函数ξ（x）以及应力函数 ∂ξ（x）/∂x:

（1）圆柱段位移函数和应力函数

（2）圆锥段位移函数和应力函数

（3）砂轮盘段位移函数和应力函数

由薄圆板厚径比计算标准（L3/R3≪1）得知，砂轮盘做薄盘自由振动，其无阻尼运动微分方程为[23]

式中:D为弯曲刚度，N/m；E0为弹性模量，GPa；ρ为面密度，kg/m2；L3为盘厚，mm；μ为泊松比；w为砂轮盘上质点的位移函数；∇2为拉普拉斯算子

当极坐标系的原点与砂轮中心点重合，且砂轮盘做简谐运动时，工具盘的理想化振动微分函数表示为

式中:ω1为砂轮盘振动角频率，rad/s；Jn（·）和Yn（·）分别为第一类、第二类贝塞尔函数；n为砂轮盘振动的节径数。

根据薄圆盘振动设计要求，通常假定其振动节径数n=0，则圆盘段的位移函数和应力函数可分别表示为

假设谐振系统左右两端处于自由状态，故而满足两端应力函数和位移函数为零。结合振动单元间的连续条件，获得边界条件

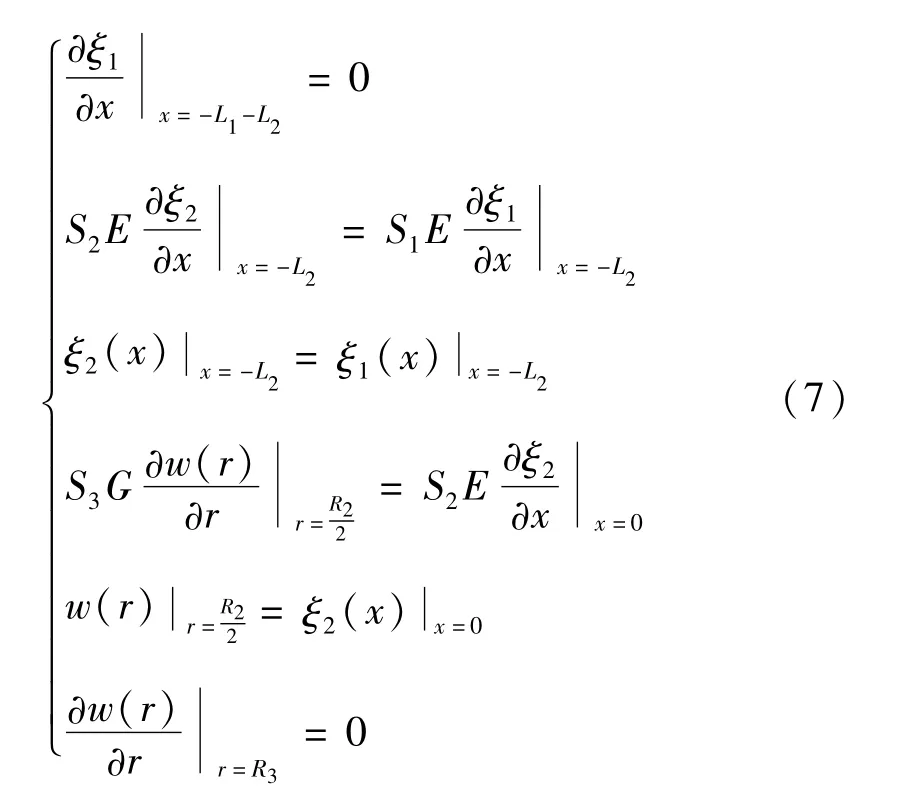
分别将该系统各部分位移和应力函数代入式（7），则系统频率方程可表示为

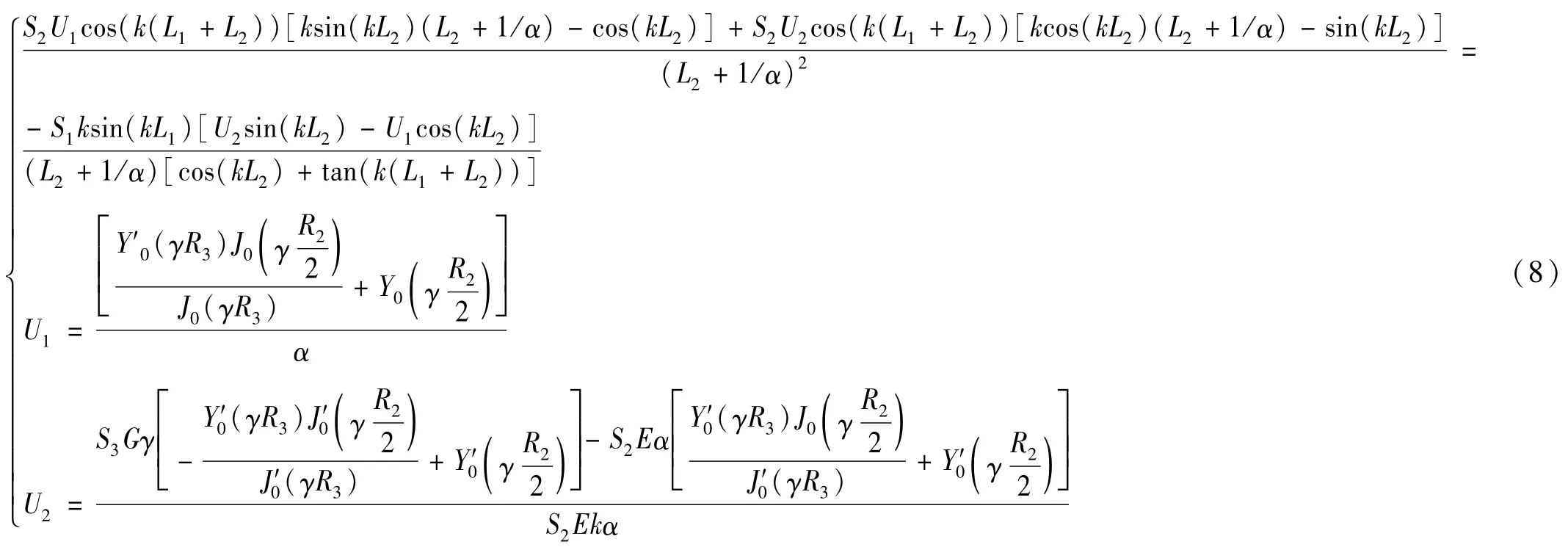
2 齿轮成形磨削谐振系统参数优化

基于本试验振动系统加工条件，为满足其加工使用强度以及实际振动效果要求，变幅杆和砂轮盘基体均选用45#钢，相关物理性能参数如表1所示。

表1 45#钢物理性能参数Tab.1 45#steel physical performance parameters

结合系统已知材料性能及尺寸参数，求解超越方程得知，在给定圆柱段L1=36.5 mm、砂轮盘半径R3=37.50 mm下，圆锥段L2=90.2 mm，且模态仿真响应谐振频率fB=33.78 kHz，如图2所示。

图2 系统模态仿真振型云图Fig.2 Cloud chart of vibration mode of system modal simulation

2.1 系统谐振频率相关特性分析

鉴于本试验激励源选用35.00 kHz换能器。故，为使系统整体处于最佳谐振状态，需对谐振频率影响因子进行探究，以此优化系统各部分尺寸参数。

基于表2所示参数基础，采用单因素变量分析法，以此探究系统各部分尺寸参数与系统谐振频率之间的相关特性关系。具体表现为:分别改变圆柱段、圆锥段以及砂轮盘厚径比等相关尺寸参数。通过SOLIDWORKS软件对系统进行三维实体建模，而后导入有限元分析软件ANSYS Workbench中。采用Block Lancazos法对自由状态下的系统进行模态、谐响应及瞬态动力学分析。设定各个材料性能参数，选用Solid95单元对系统进行4级精度的智能网格划分。模态仿真拓展阶数为37，频率搜索范围设置为20.00～40.00 kHz，并于求解器中查看各阶模态振型云图和系统模态响应谐振频率。其中，试验分9组进行，且每组仿真重复3次，取均值分析，以此减小有限元软件仿真系统误差，确保结果更具可靠性、精确性。

表2 系统仿真试验参数设计Tab.2 System simulation test parameter design

2.1.1 变幅杆尺寸与谐振频率相关特性

系统自由状态下，变幅杆各部分尺寸参数和其响应谐振频率之间的相关规律特性，如图3所示。具体表现为:系统模态响应谐振频率与变幅杆圆柱、圆锥段长度尺寸参数之间呈负相关特性。相关原因则表示为:系统整体质量与变幅杆长度呈正比，且结合牛顿第二定律可知，质量和加速度成反比关系。故，相同激励应力下，系统质量增加可致使系统工作端质点振动单元加速度降低，即整体振动频率减小。此外，增加系统整体长度，可降低其刚性和强度，进而施加相同的应力作用，变幅杆振动传输部分的变形量变大，即相当于减小系统整体材料的弹性模量E。而已知弹性模量E与波速c的平方成正比，故系统谐振频率伴随波速的减小呈下降趋势。

图3 变幅杆各部分尺寸参数与谐振频率关系特性Fig.3 The relationship between the size parameter of each part of the horn and the resonance frequency

根据相关数据拟合结果，得知其规律特性表现为:圆柱段长度平均每增加1 mm，系统谐振频率则下降0.128 kHz左右。同理，圆锥段长度平均每增加1 mm，系统谐振频率则下降0.145 kHz左右，但相比圆柱段降低幅度较大，即影响程度高于圆柱段。

2.1.2 砂轮盘厚径比与系统响应效果相关特性分析

砂轮盘厚径比与系统谐振频率、径/纵振幅比之间相关特性关系，如图4所示。具体表现为:砂轮盘系统谐振仿真频率伴随砂轮盘厚径比值的增加，呈现逐渐递增的趋势。而系统输出端径/纵振幅之比则伴随比值的增加，呈现递减的态势，与系统谐振频率形成负相关特性。相关原因分别表示为:随着砂轮盘厚径比值的不断增加，即砂轮盘半径的不断减小，系统整体的刚性及强度增强；施加相同的应力作用，变幅杆振动传输部分的变形量较小，即可等效为该部分材料的弹性模量E变大，而弹性模量E与波速c的平方成正比，波速的增大，则可增大系统谐振频率。但伴随砂轮盘厚径比的增加，薄盘振动逐渐向中厚盘振动形式演化，进而呈现出系统输出端的径/纵振幅分量之比逐渐递减趋势。

图4 砂轮盘厚径比与系统响应效果相关特性分析（L1=30.0 mm，L2=40.0 mm）Fig.4 Analysis of the correlation characteristics of the thickness-diameter ratio of the wheel disc and the system response effect（L1=30.0 mm，L2=40.0 mm）

此外，经相关仿真数据拟合结果分析得知，伴随砂轮盘厚径比的变化又可展示如下规律特性:砂轮盘厚径比平均每变化±0.01，系统谐振频率则随之变化±0.660 kHz左右。其中，在确保满足薄盘振动前提下，砂轮盘厚径比平均每变化±0.01，系统输出端径/纵振幅分量之比则随之变化∓4.1（正号示为增量，负号示为减量）。

表3、表4分别表示为系统谐振频率L9（34）正交仿真试验因素水平表及其结果，具体表现为:对比分析极差R得知，谐振频率影响因子按主次关系依次表示为砂轮盘厚径比＞圆锥段长度＞圆柱段长度。此外，本次仿真试验参数范围中的最优组合为L1=30.0 mm，L2=50.4 mm，ε=0.24。但根据其仿真验证结果得知，最优组合参数下系统固有谐振频率为20.83 kHz，与设计频率35 kHz相去甚远。故，需结合频率与系统尺寸参数之间相关变化特性，推导频率修整方程优化系统参数。

表3 正交因素水平表Tab.3 Orthogonal factor level table

表4 正交因素水平表Tab.4 Resonance frequency simulation orthogonal test results

2.2 系统谐振频率优化

经系统输出端径/纵振幅比分析可知，其与仿真频率呈负相关特性。但鉴于系统设计频率f=35.00 kHz及实际应用要求，则优先选择满足谐振频率条件。因此，基于系统各部分尺寸参数与系统谐振频率之间相关特性关系，可推得如下所示有关砂轮盘纵弯谐振频率修整方程。

式中:ΔL1，ΔL2，Δε1分别为圆柱段、圆锥段以及砂轮盘厚径之比的变化量；f1，f2分别为系统仿真及设计频率值，kHz；j为变幅杆结构总长改变量。

系统修整后各影响因子尺寸参数，如表5所示。具体表现为:结合频率修整方程以及实际加工条件，计算得出优化后圆柱段长度L1、圆锥段长度L2和砂轮盘厚径比ε分别为31.5 mm，89.6 mm，0.32。

表5 系统优化尺寸参数Tab.5 Size optimization parameters

2.3 谐振系统有限元仿真分析

2.3.1 模态仿真与分析

系统频率修整后模态向量振型云图，如图5所示，展示了变幅杆和砂轮盘耦合后，砂轮盘工作端质点实际振动方向。变幅杆中振动单元以纵向振动形式将振动传递至砂轮盘，随后砂轮盘做弯曲振动，并在其边缘处表现出最佳振动效果，即实际振幅输出最大。其次，根据工作端质点振动向量得知，砂轮盘边缘振动单元实际振动方向，位于砂轮盘径向和轴向夹角处，并可分为径向振动和轴向振动两部分，继而有效验证了齿轮成形磨削砂轮盘振动系统纵-弯谐振分析理论，并表明了系统中质点整体以纵-弯形式进行能量传输。此外，系统仿真模态谐振频率为35.01 kHz，相比35.00 kHz，误差值约为0.02%。由此得知，齿轮成形磨削纵弯谐振系统经频率修整后处于最佳谐振状态，满足系统设计及使用要求。

图5 向量振型云图Fig.5 Cloud chart of vector vibration mode

结合系统实际应用条件，需将其经由法兰盘与刀柄进行固连。此外，为确保高效率传输振动能量传至砂轮盘段，以此提升系统实际振动效果，则需计算系统振动节点位置。

为系统于约束条件下模态仿真结果，如图6所示。具体表现为:在仿真模态中添加局部坐标系，设置应变路径，得知其试验节点位置为33.75 mm左右。其次，在法兰施加约束条件下，系统谐振频率为f=36.01 kHz，相比添加法兰前频率f=35.01 kHz增加约1.00 kHz，系统谐振频率有所上升。原因可表现为:添加法兰盘并约束后，系统整体刚性及强度得到增强，施加相同激励应力作用，变幅杆振动传输部分变形量减小，即等效于系统整体材料弹性模量E相对变大。而弹性模量E与波速c平方成正比，波速的增大，可致使系统谐振频率上升。

图6 约束条件下系统模态振型云图Fig.6 Cloud chart of system vibration modal under constraints

变幅杆以及砂轮盘模态仿真振型云图，如图7所示。具体表现为:变幅杆谐振频率为27.16 kHz，砂轮盘模态频率为35.18 kHz，且系统整体仿真频率并未接近变幅杆固有频率，而是在砂轮盘固有频率附近小幅变化，与砂轮仿真频率误差仅为0.17 kHz左右。其原因可表现为:砂轮盘体积和质量相比变幅杆较大，其固有频率对系统整体谐振频率可产生较大影响，甚至改变系统固有频率的大小。此外，本文所述砂轮盘与变幅杆虽组成了齿轮成形磨削超声振动系统，但其可作为独立系统单元而发生纵-弯谐振。据相关研究表明，确保工具间连接耦合系数和其振动足够小，即直径比小于0.30和面积比小于0.10前提下，谐振系统可发生局部共振[24]。而文中变幅杆与砂轮盘连接处直径和面积比分别为0.29，0.09，满足局部共振条件。结合图7（b）砂轮盘模态振型云图可知，砂轮盘与变幅杆相连接位置变形程度最低，故可有效表明振动十分微小。因此，可有效验证基于局部共振设计理论所得齿轮成形磨削砂轮盘振动系统，出现了局部纵-弯共振现象。

图7 变幅杆及砂轮盘模态振型云图Fig.7 Modal vibration cloud diagram of horn and grinding wheel

2.3.2 谐响应仿真与分析

为探究频率修整后系统实际位移响应幅度，进行谐响应仿真试验:在圆柱端左端部给予4μm初始位移激励，频率搜索范围设为30.00～40.00 kHz，响应输出面为砂轮盘边缘工作部分，且法兰盘处于自由状态。

图8 系统谐响应振型云图Fig.8 Simulation cloud diagram of system harmonic response

砂轮盘振动系统工作端振动单元在X，Y方向的位移响应时域曲线图，如图9所示。具体表现为:当振动能量输出趋于稳定后，由于砂轮盘纵弯谐振作用，使X，Y方向均产生了位移。其中:X方向为纵向振动的平行方向，且振幅值相比初始激励幅值（4μm）放大1～2倍；而Y方向为纵向振动的垂直方向，振幅远小于初始激励幅值。此外，经由振动单元输出位移轨迹曲线观察得知，系统整体输出状态符合谐振波振动形式，故系统随激励源做简谐振动得以有效验证。

图9 砂轮盘工作端一点振动曲线Fig.9 Response curve of the particle unit at the working end of the grinding wheel

采用相关数据分析软件，对输出端质点X，Y两方向位移进行数据拟合后，所得工作端振动质点单元轨迹拟合曲线，如图10所示。相关特性表现为:Y振动方向质点单元激励源响应幅值远小于X振动方向质点单元，系统总体振动输出形式与单一纵向相近。此外，经模拟所得二者位移幅值数据拟合曲线得知，该曲线轨迹为一平面椭圆，相符于输出端质点单元轨迹预测结果。由此，可验证齿轮成形磨削中砂轮盘产生弯振，以及工作端质点单元以纵-弯的形式传输系统能量。

图10 工作端质点单元振动仿真轨迹拟合曲线Fig.10 Fitting curve of vibration simulation trajectory of particle unit at working end

3 系统阻抗特性及谐振效果测试

3.1 阻抗测试与分析

采用PV70A型号阻抗分析仪，对实际加工并装配后的振动系统进行阻抗特性测试所得结果，如图11所示。具体表现为:系统的导纳圆圆度较好、阻抗-相位-频率曲线比较规则，证明两者谐振点及其附近点的振动效果较为理想。而动态电阻为95.5Ω，则表明所设计的声学系统内阻较小，换能器与变幅杆、砂轮盘的阻抗匹配度较高。其中，系统整体品质因数较为理想，即表示为其声-电转换效率较高。

图11 砂轮盘振动系统阻抗测试Fig.11 Impedance test of the vibration system of the grinding wheel

表6所示参数为齿轮成形磨削纵弯谐振系统设计、仿真及试验频率三者之间的相对频率误差。其中，ΔE和ΔF的频率误差分别为0.20%，0.34%，相对仿真与设计频率之间的误差（ΔD）较大。原因可表现为:①理论设计时忽略了螺母以及各连接部分间隙的影响，而实际螺母的质量对系统整体的刚度和质量均有影响，继而致使系统谐振频率产生变化；②理论设计及仿真分析时，近似认为变幅杆与砂轮盘间通过螺栓实现理想化的刚性连接，但实际情况下，螺母因预紧力的不足，可能会影响各组成部分间的连接刚度，从而导致理论与仿真之间的非协调性；③实际加工过程中，由于材料各力学性能参数与设计、仿真参数以及各部分零件尺寸的加工和配合精度之间均存在一定误差，进而系统谐振频率理论值与实测值间难以完全保证一致性。

表6 理论、仿真和试验谐振频率比较Tab.6 Comparison of theoretical，simulation and experimental resonance frequencies

3.2 谐振效果测试与分析

砂轮盘纵弯谐振系统径/纵响应振幅测试现场，如图12所示。具体表现为:选用SZ12型智能超声波发生器进行成形砂轮纵弯谐振系统振动性能测试。而后调试发生器至工作稳定状态下，通过Keyence LK-G10型激光位移传感器，分别测量砂轮盘纵向及径向分量谐响应振幅。其中，数据采集器将所测高频机械振动信号进行收集和模数转换，经计算机相关软件计算输出相关振幅时域响应曲线。

图12 振动系统径/纵响应振幅测试现场Fig.12 Vibration system diameter-longitudinal response amplitude test

系统谐振状态下，砂轮盘工作端和侧面质点单元振幅实际测量结果，如图13所示。具体表现为:在砂轮盘端面边缘及侧面分别均布选取8个位置点进行测振，每处重复3次，取均值。结果表明，纵向振幅响应状态、径向分量振幅响应状态以及系统整体振动耦合性能均比较稳定，由此证明该声学系统的传声效果较好。此外，经振幅分量均值分析可知，纵向分量均值稳定在5.2μm左右，径向分量均值稳定在1.1μm左右。相比仿真结果而言，振幅值和径纵比均有所降低，原因可表现为:①超声波发生器定频性能不够稳定，以及测量过程中周围环境的扰动等均会影响测量结果的准确性，从而具有一定的系统误差；②系统装配过程中，各连接部位因间隙存在不可避免，可造成一定程度上的能量损失，继而使实际响应振幅因能量衰减而降低；③超声波在系统中传播时，因法兰盘、砂轮盘和变幅杆连接部位存在一定的波反射，从而存在能量损耗、杂波、系统整体阻抗失配等问题，进而致使振幅的衰减。

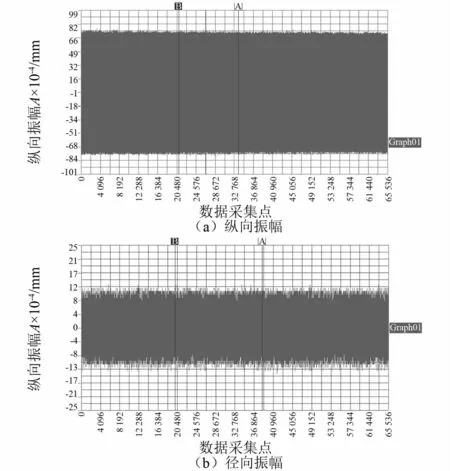
图13 砂轮响应端振幅测试曲线Fig.13 Amplitude test curve of the response end of the grinding wheel

工作端任一质点振动轨迹实测数据拟合曲线，如图14所示。其中，提取纵向振幅和径向振幅响应曲线中单周期内数据点进行拟合。拟合结果曲线表现为近似椭圆形的轨迹，与仿真结果相近。但，此轨迹曲线并非完全形成封闭圈，原因可表现为:纵向和径向振动之间存在一定的相位差，以及周期振动过程中振幅难以保证完全均匀性和稳定性等。其次，砂轮盘工作端镀有磨粒，其反射作用亦可引起一定的误差。此外，碍于激光位移传感器的精度不足，单周期内所采集数据点较少，继而致使拟合所得椭圆展现得不够圆滑。

“五星牌”手表除游丝、发条和钻石轴承为市场购买外，其它零部件均为试制小组自己生产，其摆频为18000次/小时，走时误差为-60～-90秒/日。天津试制成功手表后，受到国家领导人和轻工部门的高度重视，毛泽东主席曾对此作出：“手表要多生产一些，价格再降低一些”的重要批示。

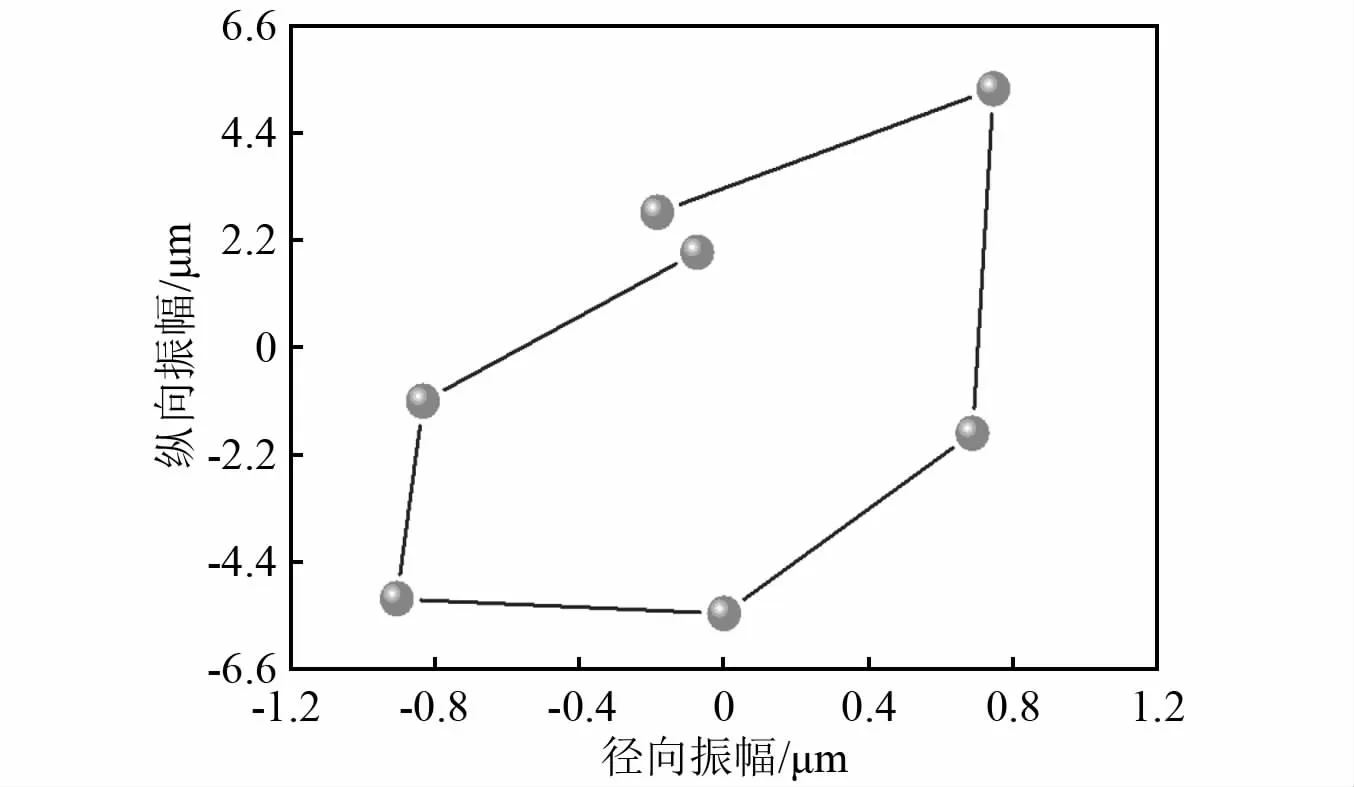
图14 工作端质点单元实测振动轨迹拟合曲线Fig.14 Fitting curve of measured vibration trajectory of particle unit at working end

结合图10和图14对比分析可知，砂轮盘工作端面任一质点仿真与实测结果拟合轨迹相似，均表现为近似椭圆形曲线。由此表明，齿轮成形磨削砂轮盘纵弯谐振系统中参与磨削加工的磨粒，均以椭圆周期形式运动。其中，纵向振动作用于磨削加工的磨深方向，形成磨粒与工件高频分离-接触-分离的作用模式；径向振动分量则等效于在垂直进给方向拉伸了磨粒沿进给方向的轨迹，形成一个倾斜一定角度的椭圆运动轨迹。而椭圆振动形式可改变单颗磨粒普通磨削状态下的纯直线运动，增加了磨削轨迹的干涉程度以及磨粒与工件的分离时间，增加砂轮有效磨粒数的同时也促进了磨削液的流通，从而在一定程度上减小了单颗磨粒的磨削力和磨削热。且在单位时间内，增大了磨痕的宽度，这导致磨除体积增加，故而可提高材料的去除率。此外，基于超声振动的高频破碎作用，椭圆磨削可使沙粒具有自锐性，延长工具盘的使用寿命，更有助于降低加工表面粗糙度，提升加工质量等[25]。

保持工具盘半径给定情况下，纵向振幅大小与测量位置点半径之间的关系，如图15所示。具体表现为:在砂轮盘端面，沿其半径由内向外选取9处位置点进行测振，而碍于螺母和垫片的影响，测振点半径范围选为16.0～37.5 mm。结果表明，工作端质点单元纵向振幅，伴随测振点半径的增加呈现先减后增的趋势。在测振半径为23.5 mm附近振幅达到最小，并接近为零，故在此测振点环形区域内为砂轮盘振动节圆位置。而测振点半径大于节圆半径时，纵向振幅则又表现为逐渐递增趋势，至37.5 mm处测振点振幅达到最大。故，可认为成形砂轮盘工作面处于波峰附近。

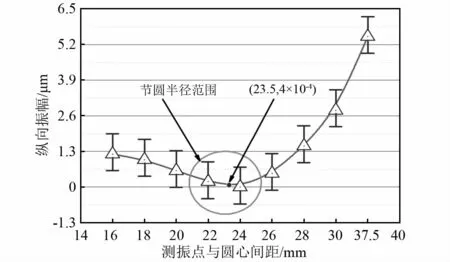
图15 振幅随测振点半径大小的变化特性Fig.15 Variation characteristics of amplitude with radius of measured vibration point

砂轮盘做节圆型振动响应结果，如图16所示。具体表现为:将系统放置为竖直自由状态；连接SZ12型智能超声波发生器与换能器；启动发生器并调节调频螺母，使系统工作在谐振频率f=34.93 kHz附近，并于砂轮端面撒少量细沙。由系统实际响应结果可知，沙粒迅速以圆盘中心为圆心形成同心圆环，而圆环的产生表示沙粒所处位置振动最弱，以此证明了砂轮盘在变幅杆纵向振动激励下做节圆型横向弯曲振动，有效验证了仿真结果。

图16 工具盘节圆振动测试Fig.16 Tool disc pitch circle vibration test

4 结 论

（1）根据ANSYS Workbench有限元仿真结果得知，本文基于局部共振理论可对成形砂轮纵-弯谐振系统进行有效设计，且砂轮可独立于振动系统而存在纵弯谐振，即局部纵-弯共振现象。此外，砂轮盘工作端磨粒质点单元径纵振幅比a与其厚径比ε、系统固有频率间均呈负相关特性。其中，系统固有频率可结合文中所述频率修整方程进行优化，并以此获得系统各部分满足设计频率所需几何尺寸。

（2）经系统优化参数下磨粒质点单元运动特性分析得知，系统耦合后砂轮工作端振动模式变现为径/纵复合振动，且纵、径方向振型均近似为正弦曲线，径纵比a=0.193。系统整体谐振频率伴随复合变幅杆各段长度尺寸增加，呈逐渐递减趋势，而与工具盘半径呈负相关特性。此外，因超声波波长伴随谐振频率下降呈递增态势，进而造成波峰和波谷位置不断变化，使纵向及径向响应振幅产生一定程度的波动。

（3）磨削端面上任一质点的振动轨迹仿真及试验结果表明，磨粒在垂直于进给方向平面内拉伸，形成倾斜一定角度的椭圆形振动轨迹，并周期性地参与磨削加工。超声谐振试验结果表明，成形砂轮工作端磨粒单元振型和谐响应振幅比较稳定，对该预期效果进行了有效验证，并为后续局部共振设计理论，特别是大负载型齿轮成形磨削砂轮盘纵弯谐振系统的设计，提供了参考基础。