泵喷分布式脉动压力激励下泵喷艇体耦合系统振动声辐射
2021-10-11黄修长苏智伟师帅康饶志强华宏星
黄修长, 苏智伟, 师帅康, 饶志强, 华宏星
(1.上海交通大学 振动、冲击、噪声实验室,上海 200240;2.上海交通大学 机械系统与振动国家重点实验室,上海 200240)
螺旋桨、泵喷等推进器在表面脉动压力激励下,一方面会产生结构振动直发声以及流噪声直发声;另一方面会通过轴系、定子等传递激励艇体,导致艇体产生强烈的声辐射。因此,推进器-轴系-艇体的耦合振动声辐射研究受到广泛关注[1-3]。
目前已针对螺旋桨-轴系-艇体耦合系统的振动噪声特性开展丰富的研究,明确了螺旋桨激励下螺旋桨-轴系-艇体耦合系统的声振响应特性[4-5]。但上述分析均采用在螺旋桨桨毂或0.7R处施加集中力(R为螺旋桨半径),无法考虑分布式载荷的相位不同以及螺旋桨空间模态特性对响应的影响。为考虑上述问题,部分学者在分析螺旋桨-轴系耦合系统的响应或螺旋桨的流固耦合响应时,采用条带法将随机宽带力映射到螺旋桨结构网格上进行施加[6],或利用面元法和有限元法(finite element method,FEM)耦合将计算得到的脉动压力施加到结构网格[7-8]。
泵喷推进器作为一种组合推进器,由于具有较螺旋桨更优越的推进及静音性能而被广泛应用。泵喷推进器的激励力更为复杂,其脉动压力是在导管、定子、转子吸力面和压力面上呈复杂空间分布的力,在该空间分布力作用下会激励起不同模态产生复杂的响应,其响应特性和响应机理更加复杂。目前针对泵喷推进器的研究主要集中在3个方面:一是水动力性能、表面脉动压力激励特性、流场特性等的研究[9-10];二是泵喷参数(如间隙、导管几何参数和定转子几何参数等)对水动力学性能、脉动压力等的影响[11-12];三是推进器脉动压力激励下艇体的声辐射特性以及新型结构(如锯齿后缘导管)的降噪效果[13]。但对于泵喷激励下泵喷-轴系-艇体耦合系统振动声辐射的研究鲜见公开报道。对于泵喷推进器激励下的艇体振动声辐射响应,泵喷推进器同时通过推进轴系激励艇体以及通过导管-定子激励艇体,这两种途径的传递特性、传递幅值相对大小等仍不明确。
本论文考虑suboff艇后泵喷推进器的激励力为转子、导管和定子上的分布式脉动压力分布,通过插值的方法把流体脉动压力映射到推进器结构湿表面,建立了泵喷-轴系-艇体的耦合动力学模型,获得了其结构振动声辐射响应,并分析了通过轴系激励艇体、通过导管-定子激励艇体这两条传递途径的振动声辐射响应特性。
1 理论基础
1.1 suboff艇后泵喷表面脉动压力计算
不考虑推进器内部流场空化影响,可假设流体为不可压缩黏性单相流,基于雷诺平均纳维-斯托克斯(reynolds-averaged navier-stokes,RANS)的控制方程可写为[14]
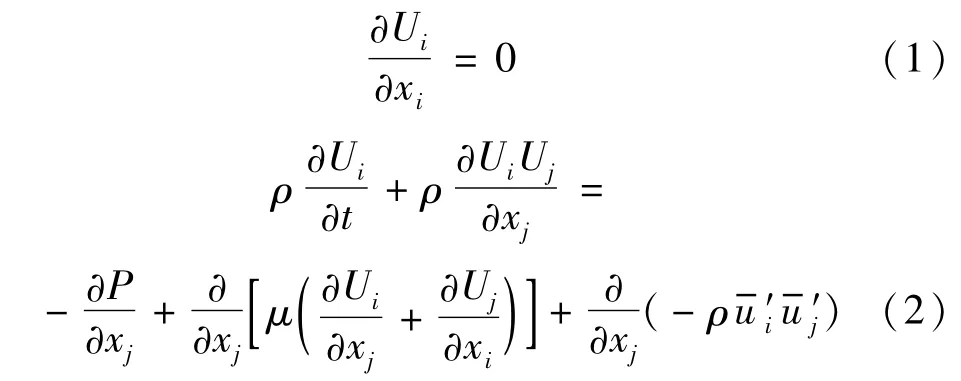
式中:i,j=1,2,3;ρ为流体密度;xi和xj分别为笛卡尔坐标系下3个方向的坐标分量;P为雷诺平均压力;Uj和u′i分别为平均速度和脉动速度;μ为流体动力黏度系数;为雷诺应力项,为了使式(2)封闭,引入涡流黏度vt,雷诺应力可写为
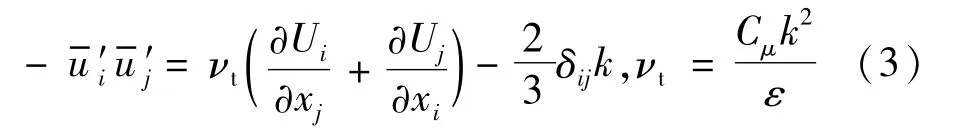
式中:k为雷诺时间平均下湍流动能;Cμ=0.09。采用剪切应力输运(shear stress transfer,SST)k-ω湍流模型进行模拟。
1.2 泵喷-轴系-艇体耦合系统振动声辐射模型
采用耦合有限元法开展泵喷-轴系-艇体耦合系统的动力学建模
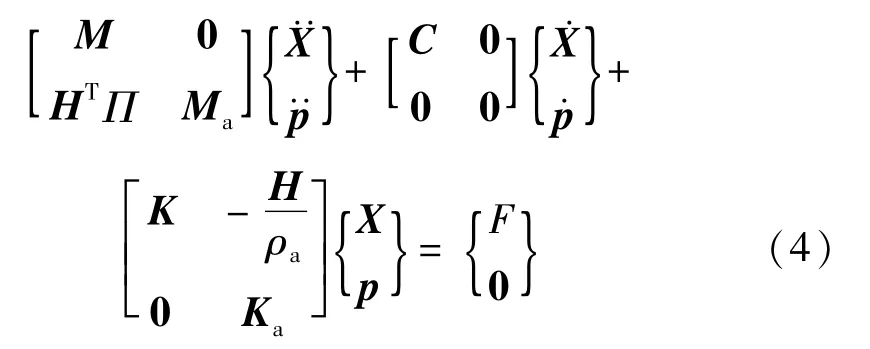
式中:M和K分别为泵喷-轴系-艇体耦合系统的质量和刚度矩阵;C为阻尼矩阵,C=αM+βK;X为结构的位移向量;p为流场中的声压向量;F为泵喷的分布式脉动激励力;Ma和Ka分别为流体的质量矩阵和刚度矩阵;H为流固耦合矩阵;∏建立了结构湿表面上的节点法向位移与结构振动位移向量X之间的关系。Ma,Ka和H的表达式分别为
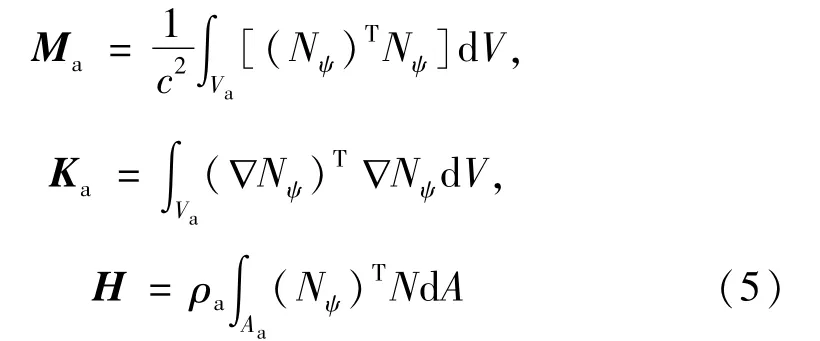
式中:N和Nψ分别为结构和流体的插值形函数;ρa为流体密度;c为流体中波速。
由结构湿表面的法向振速viα,利用直接边界元法(boundary element method,BEM)求得湿表面上的声压piα以及场点声压pj[15]
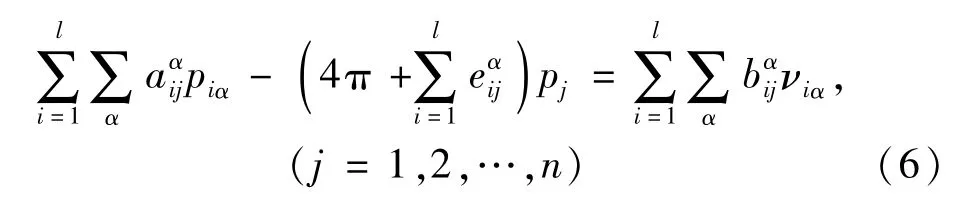
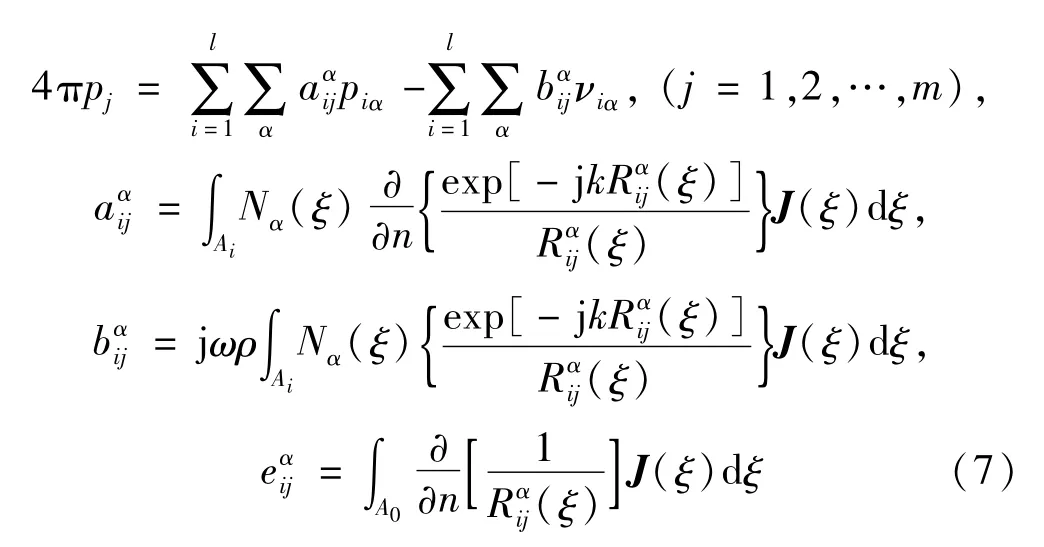
式中:J(ξ)为Jacobian矩阵;Ai为第i个单元的面积;(ξ)为第j个场点与泵喷-轴系-艇体耦合系统结构湿表面上第i个单元的第α个节点之间的距离;N(ξ)为边界元中声压的插值形函数。
1.3 表面分布式脉动压力和结构湿表面节点力映射
将计算流体动力学(computational fluid dynamics,CFD)模型中转子、定子、导管表面单元的压力以及泵喷结构湿表面的节点导出,通过径向基函数插值将流体单元节点的压力映射到泵喷结构湿表面节点上。假设空间存在一组点群xj及点群上的函数值fj(j=1,2,…,N),可构建各点之间的距离函数ϕ(‖x-xj‖)与函数值之间的关系

式中:ϕ(‖x-xj‖)为径向基函数,它是插值点与目标点之间距离的函数;λj为径向基函数的系数。通过xj可建立点群之间的λj系数求解线性方程组。空间任意点上的函数值f(x)则可通过式(8)求解。具体计算时首先找到泵喷结构湿表面单元中心附近的一组流体节点及压力值,并求解径向基函数插值系数,然后将泵喷结构湿表面单元中心代入式(8)中求解泵喷结构湿表面单元上的压力分布。在求得泵喷结构湿表面单元的压力分布后,将压力乘以面积得到面单元上的集中力,将集中力按节点数平均分配到各个节点上,即可得到每个节点上的集中力分布。在每个时刻进行径向基函数插值即可得到时域中的结构湿表面节点的三向集中力。利用傅里叶变换可得到频率域结构湿表面节点的三向集中力。
2 数值模型
研究对象为suboff艇后泵喷推进器模型,如图1所示。泵喷-轴系-suboff艇参数,如表1所示。壳体厚度为6 mm,并采用T型加强筋进行加强,纵向方向有4个舱壁;泵喷推进器通过定子支撑在壳体艉部。泵喷-轴系模型见图1,推进轴系的长度为0.89 m、直径为0.022 m,通过艉后轴承支撑在壳体艉部以及通过推力轴承支撑在最后一个隔舱壁的中心。艉后轴承的横向和垂向刚度分别为4.5×109N/m,1.7×108N/m;推力轴承的纵向、横向和垂向刚度分别为6.6×108N/m,2.3×108N/m和6.7×108N/m。壳体、加强筋、轴系、泵喷定子和导管的材料为钢,其密度、弹性模量和泊松比分别为7 850 kg/m3,2.1×1011Pa,0.3。 转子的材料为青铜,其密度、弹性模量和泊松比分别为8 790 kg/m3,1.1×1011Pa,0.3。 结构阻尼均取为0.001。
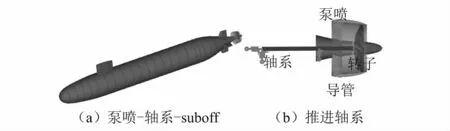
图1 泵喷-轴系-艇体耦合系统Fig.1 Pump-jet-shafting-suboff system

表1 泵喷-轴系-suboff艇参数Tab.1 Parameters of pump-jet-shafting-suboff system
2.1 CFD模型和计算验证
创建泵喷-轴系-suboff的CFD计算区域,如图2(a)所示,将计算域划分成静止域和旋转域,静止域包含定子、艇体计算域和导管计算域,将转子所在旋转域设置为滑移网格,两个计算域之间的交界面设置为interface边界条件,进行数据传递。计算中远前方入口设置为速度入口条件,远后方出口设置为压力出口条件,外围远场边界与入口一样为速度入口条件,转子、定子及导管等固体表面采用无滑移固体壁面条件。部分进行流体计算的面网格,如图2(b)所示。结合网格无关性分析结果,选择合适的网格密度进行流域网格划分。计算域网格共计2 760万,其中:艇体域网格为1 000万;泵喷定子域网格数量为660万;泵喷转子域网格为1 100万。艇体表面和泵喷推进器均划分精细边界层网格,目标Y+值为1。
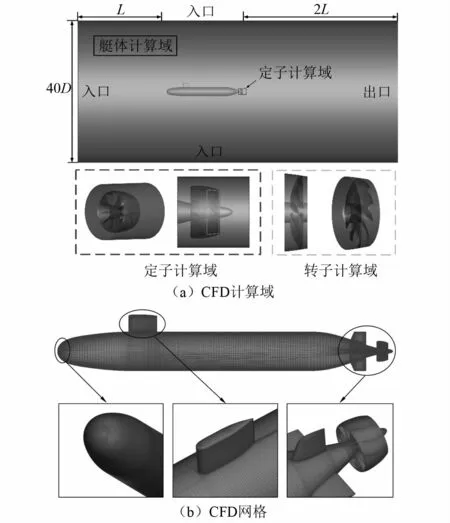
图2 suboff艇后泵喷的计算域和CFD网格Fig.2 Computational domain and CFD model of the behind-hull suboff
计算工况为进速9.42 m/s,转子转速1 824 r/min,进行非定常计算,设置时间步长为4.568 7×10-5s,保证转子每个时间步旋转0.5°,计算的最高频率为10 944 Hz,采样频率为21 888 Hz。数值计算的收敛性残差满足:连续性残差收敛在10-5以下,3个方向速度残差均在10-6以下,湍动能k残差低于10-7。
CFD数值求解采用商业软件ANSYS Fluent进行,采用SST k-ω湍流模型,压力、速度耦合求解采用SIMPLEC(semi-implicit method for pressure-linked equations consistent)方法,其他项均采用二阶迎风格式。
采用对suboff艇和泵喷单独进行CFD计算验证的方法对建立的模型进行验证。对suboff艇体进行验证时,保留图2中的suboff网格,流域和网格密度与图2相同。采用上述网格模型对进速3.051 m/s的工况进行计算,得到全附体suboff艇阻力(103.2 N)与实测阻力(102.3 N)误差为0.9%[16],同时得到的桨盘面处的轴向伴流结果与试验结果相似,如图3所示。对泵喷进行验证时,采用与图2相同的流域、网格密度(其中:Grid2与图2中网格数量相同;Grid3将转子域中网格增加40%)和计算设置,对一五叶前置定子七叶转子泵喷进行计算,如图4所示。将计算结果与空泡水筒中的试验结果进行对比,采用Grid2推力最大误差为3.59%,最小误差为0.23%,扭矩最大误差为5.5%,效率的最大误差为5.17%,精度较高,增加网格数量后(Grid3)增加了计算成本,精度提高不明显,故采用Grid2满足分析要求。
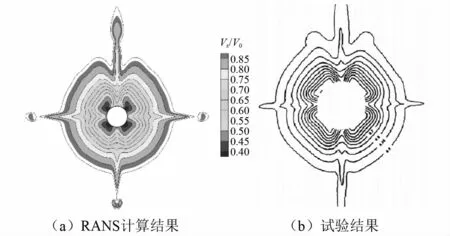
图3 桨盘面处轴向伴流对比Fig.3 Comparison of axial velocity in the rotor plane
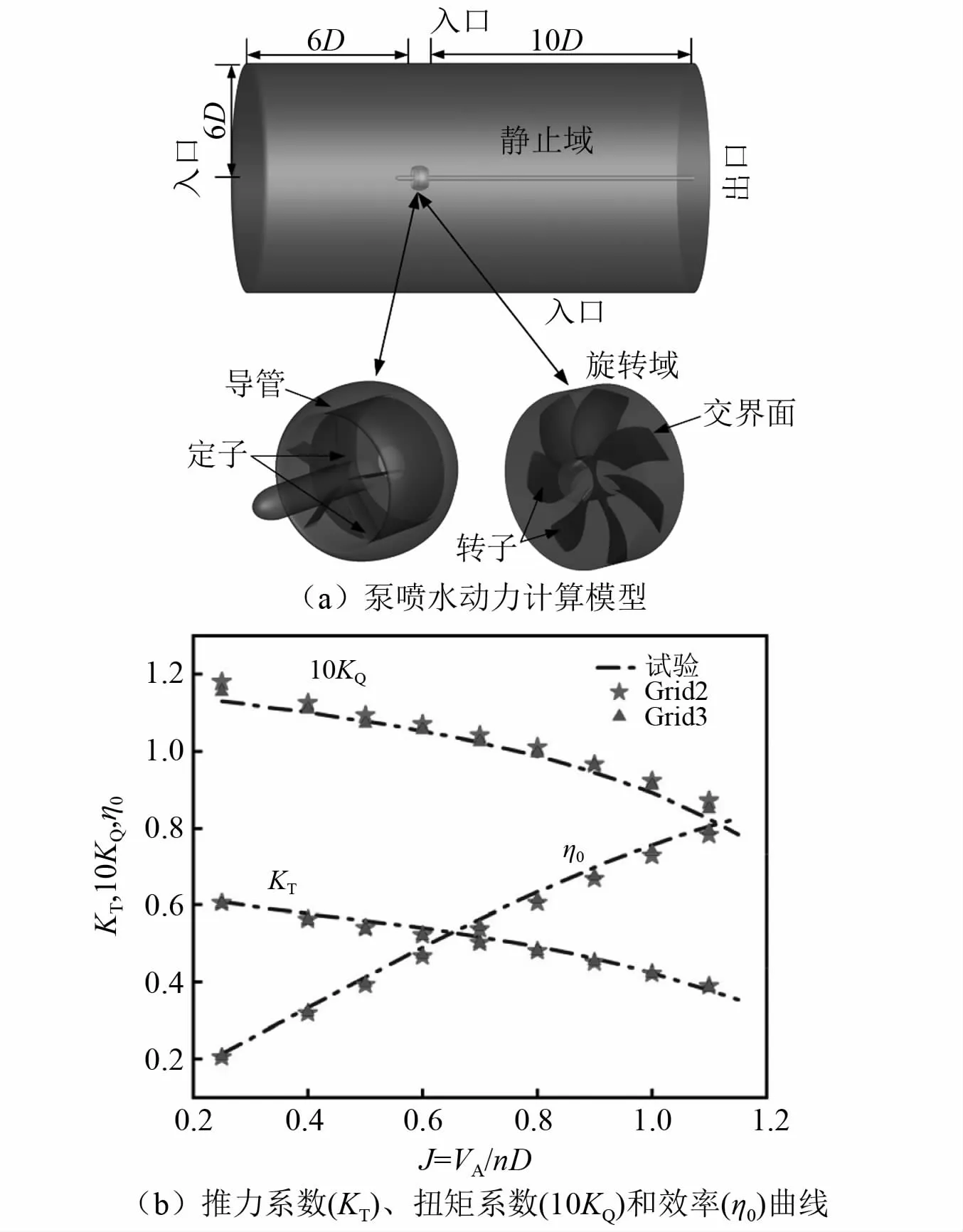
图4 泵喷水动力性能计算模型和试验验证Fig.4 CFD model and experimental validation for propulsion performance of the pump-jet
2.2 结构动力学模型
在ABAQUS软件中建立泵喷-轴系-艇体耦合系统的结构有限元模型,如图5所示。壳体采用33 861个S4R单元进行模拟,加强筋采用4 354个B31单元进行模拟,舱壁采用4 362个S4R单元进行模拟。定子、转子和导管采用22 641个C3D8实体单元进行模拟。推进轴系采用91个B31梁单元进行模拟。为考虑流固耦合,在泵喷-轴系-艇体耦合系统的结构有限元模型外建立圆柱形的水体,在结构有限元模型的湿表面和水体模型的表面之间建立压力和速度耦合条件。其中圆柱形水体的长度和直径分别为6 600 mm,2 500 mm(直径为6倍导管最大直径)。水体采用2 601 967个AC3D8声学单元进行模拟。水的密度和体积模量分别为1 000 kg/m3和2×109Pa。在水体外表面施加无反射声学边界条件。将泵喷导管、定子和转子湿表面以及艇体湿表面的速度导出到LMS VirtualLab中,利用直接边界元法进行声辐射的计算。结构单元和声辐射单元的网格大小为5 mm,根据拇指法则,结果在600 Hz以内具有可信度[17]。
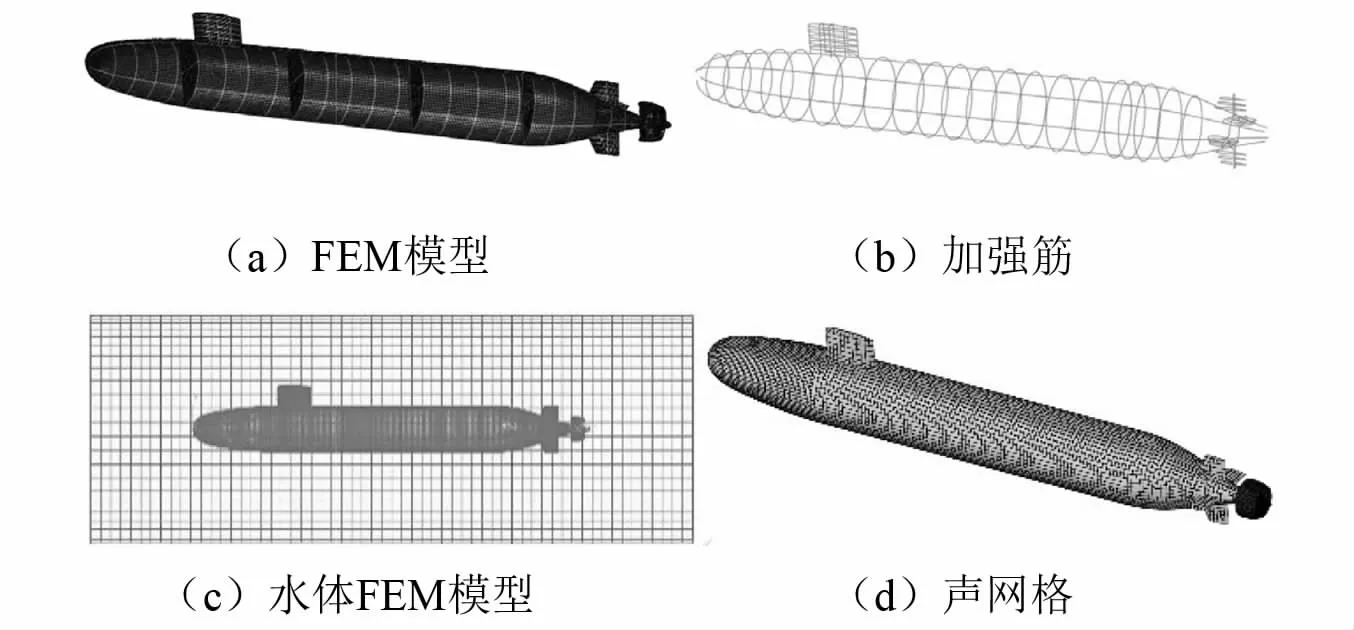
图5 泵喷-轴系-艇体耦合系统结构振动声辐射模型Fig.5 Vibro-acoustic model of coupled pump-jet-shafting-suboff system
3 仿真结果与分析
3.1 表面脉动压力
取出某个转子叶片表面0.7R,0.8R,0.9R和相应转子区域对应的导管内壁面某点的脉动压力,其频谱结果如图6所示。由图6可知,叶片的脉动压力以轴频30.4 Hz及其倍频为主,导管上的脉动压力以叶频273.7 Hz(9倍轴频)和2倍叶频547.4 Hz为主。总体而言,导管上的脉动压力幅值比转子叶片上监测点的脉动压力幅值大1~2个数量级。
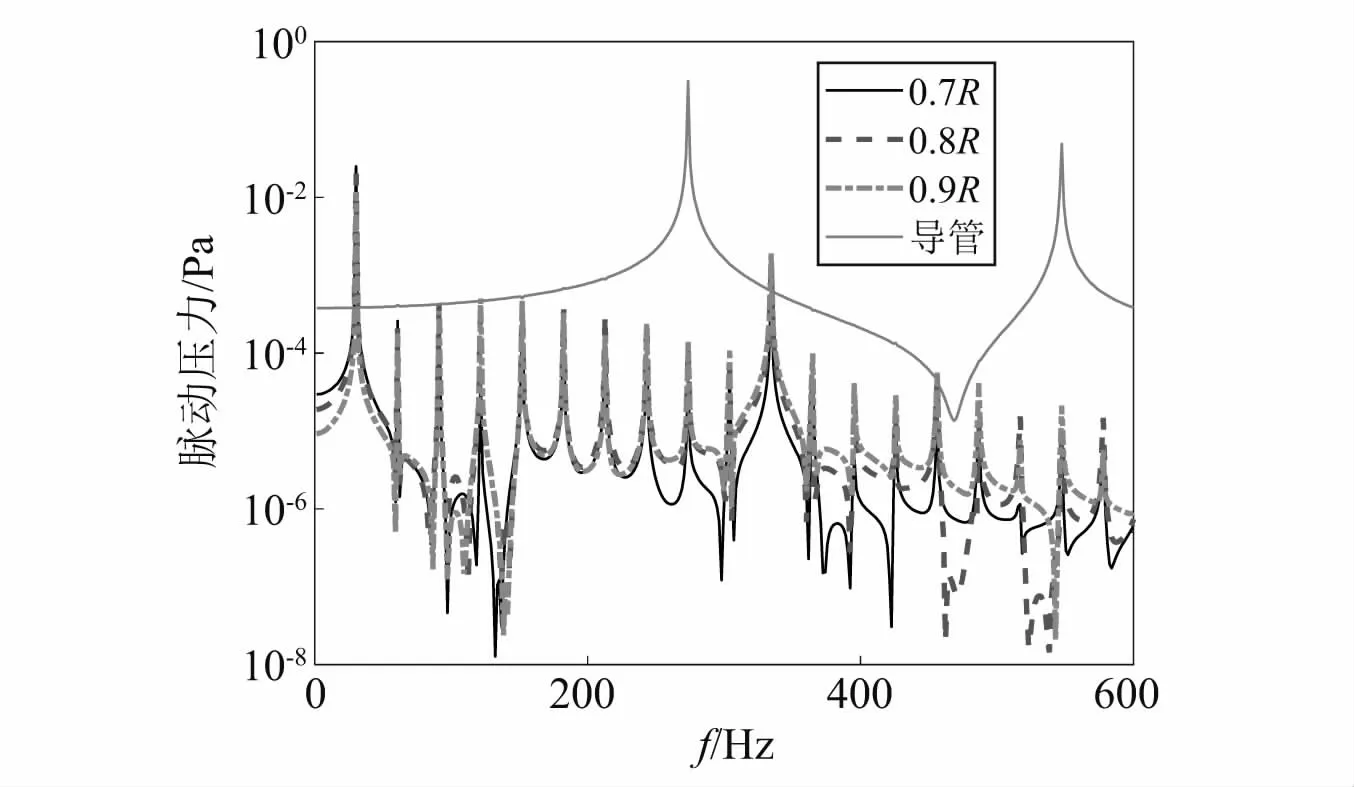
图6 转子不同半径处和导管的表面脉动压力频谱Fig.6 Spectrum of pressure on the different radius of rotor surface and the duct
转子纵向、横向和垂向合力的时程曲线和频谱,如图7所示。由图7可知,由于不同转子叶片上的脉动压力相位不同,叠加后各个方向的脉动力在叶频及其倍频处出现较大的峰值,在轴频及其倍频处也表现为峰值,纵向脉动力的幅值大于垂向和横向脉动力。随着频率的增加,脉动力的幅值呈衰减趋势。
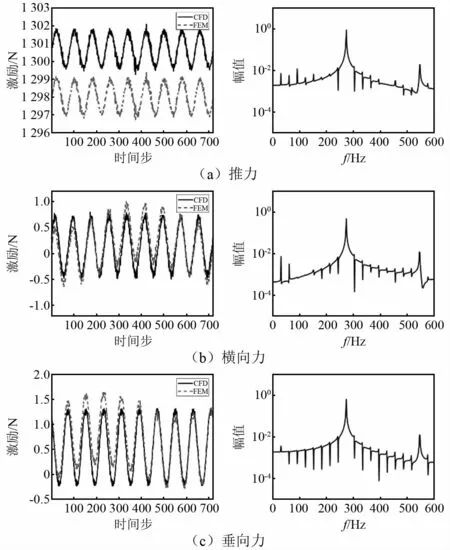
图7 转子三向脉动力的时程曲线和频谱Fig.7 Time-history,spectrum of pulsation force in three directions for the rotor
图8给出了CFD计算得到的表面脉动压力结果和插值后导入到ABAQUS中结构湿表面脉动压力结果的对比,给出了转子压力面和导管内壁面的结果。由图8可知,采用径向基函数插值后,脉动压力的分布和幅值均能够保证足够的精度。

图8 分布式脉动压力的CFD结果和FEM结果比较Fig.8 Comparison of fluctuation pressure distribution on surface of propeller,duct between CFD and mapped result in FEM
3.2 模态结果与分析
对泵喷-轴系-艇体耦合系统动力学模型开展模态分析,得到典型模态结果如图9、表2所示。

表2 耦合系统模态频率列表 Tab.2 List of modal frequencies of the coupled system Hz

图9 泵喷-轴系-艇体耦合系统典型模态Fig.9 Typical modal shapes of the coupled pump-jet-shafting-suboff system
下面计算泵喷-轴系-艇体耦合系统的振动声辐射响应。考虑4种载荷施加方法:一是将导管、转子和定子上的脉动压力施加到结构网格上(‘Pumpjet’);二是仅将转子上的脉动压力施加到结构网格上(‘Ro-tor’);三是对转子叶片上的脉动压力进行求和,将每个叶片上的三向集中力施加到转子叶片0.7R处(‘0.7R’);四是对整个转子的脉动压力求和,将整个转子的三向集中力施加到桨毂中心(‘Hub’)。
3.3 通过轴承的传递力结果与分析
对通过各个轴承的传递力进行分析。推力轴承和艉后轴承在不同载荷施加方式下的多向传递力,如图10所示。对于推力轴承,通过其传递的三向力对于‘Pumpjet’和‘Rotor’基本重合,‘0.7R’将使结果偏大;‘Hub’将使212.9 Hz以前的结果偏小。推力轴承纵向传递力的最大响应峰值为轴频30.4 Hz。5个显著的峰值分别为209.9 Hz(轴系一阶纵振),212.9 Hz(7倍轴频),243.3 Hz(8倍轴频)和273.7 Hz(9倍轴频,即叶频)以及547.5 Hz(18倍轴频,即2倍叶频)。轴系一阶纵振的峰值频率显著和相邻的峰值具有可比性。一些小的响应峰值出现在334.6 Hz(艇体一阶纵振),360.4 Hz,391.3 Hz(轴系二阶纵振),486.6 Hz和577.9 Hz。对于推力轴承垂向传递力,‘0.7R’和‘Hub’施加方式在叶频273.7 Hz处出现峰值,但是在‘Pumpjet’和‘Rotor’情况下并未出现。主要的峰值频率为30.4 Hz,118.6 Hz(轴系一阶弯曲),121.7 Hz(4倍轴频),243.3 Hz(8倍轴频),365.0 Hz(12倍轴频),415.2 Hz(在泵喷处出现最大变形的轴系弯曲模态),517.0 Hz(17倍轴频)和547.5 Hz(18倍轴频)。推力轴承横向传递力和垂向传递力具有类似的规律,主要的峰值频率为30.4 Hz,118.6 Hz,121.7 Hz,152.1 Hz(5倍轴频),243.3 Hz,304.1 Hz(10倍轴频),365.0 Hz,416.7 Hz(在泵喷处出现最大变形的轴系弯曲模态)和517.0 Hz。除了轴频,4个最大的响应峰值出现在121.7 Hz,243.3 Hz,365.0 Hz和415.2 Hz;小的峰值出现在273.7 Hz,334.6 Hz(11倍轴频)。推力轴承纵向传递力的幅值比横向和垂向传递力大一个数量级。
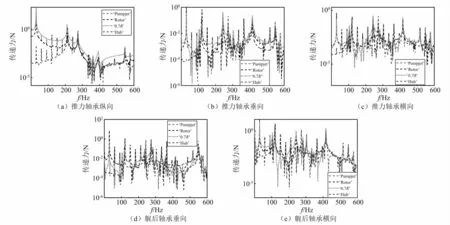
图10 推力轴承和艉后轴承的力传递Fig.10 Force transmission by thrust bearing and stern tube bearing
对于艉后轴承传递力,可得到类似结论。垂向传递力的显著峰值出现在30.4 Hz,118.6 Hz,121.7 Hz,152.1 Hz,182.5 Hz(5倍轴频),212.9 Hz(7倍轴频),243.3 Hz,304.1 Hz,365.0 Hz,416.7 Hz和547.5 Hz。横向传递力的显著峰值出现在30.4 Hz,118.6 Hz,121.7 Hz,152.1 Hz,182.9 Hz,212.9 Hz,243.3 Hz,304.1 Hz,365.0 Hz,416.7 Hz和517.0 Hz。在艉后轴承处的垂向和横向传递力比推力轴承处的垂向和横向传递力大一个数量级。
在上述峰值频率中,大部分为泵喷推进器脉动压力的轴频及其倍频,以及结构的模态,如艇体一阶纵振模态、轴系的一阶和二阶纵振模态,但是‘Hub’无法激励起丰富的脉动压力峰值频率和模态频率。
3.4 水下声辐射结果与分析
泵喷-轴系-艇体耦合系统的水下辐射声功率(sound radiation power,SRP)和均方振速(mean-square velocity,MSV)级,如图11所示。不同的载荷施加方式下辐射声功率和均方振速的变化规律和传递力类似。可见转子上分布式脉动压力引起的振动声辐射将占主导作用,主要的峰值频率出现在30.4 Hz,91.3 Hz(3倍轴频),121.7 Hz,152.1 Hz,182.5 Hz(6倍轴频),209.9 Hz,212.9 Hz,243.3 Hz,273.7 Hz,304.1 Hz,334.6 Hz(艇体一阶纵振),365.0 Hz,395.4 Hz(13倍轴频),416.7 Hz,456.2 Hz(15倍轴频),486.6 Hz(16倍轴频),517.0 Hz,547.5 Hz和577.9 Hz。 一些小的峰值出现在209.9 Hz,235.7 Hz和252.4 Hz。并且在艇体一阶纵振模态334.6 Hz处的响应比相邻峰值均大。传递力中在轴系一阶弯曲模态118.6 Hz出现的峰值在辐射声功率和均方振速中未得到明显体现,这是由于轴系弯曲模态通过艉后轴承传递的力以及通过推力轴承传递到舱壁的力都难以有效激励起艇体的振动声辐射。推力轴承传递力在轴系一阶纵振模态209.9 Hz出现的峰值在辐射声功率和均方振速中仍具有较大的峰值。为进一步研究不同方向脉动压力激励起的艇体声辐射,取出泵喷的纵向脉动压力施加到转子、定子和泵喷表面,将得到的辐射声功率和同时在泵喷表面施加三向脉动压力的结果进行比较,如图11(c)所示,可见在2倍轴频以上,声辐射主要由纵向脉动压力主导。
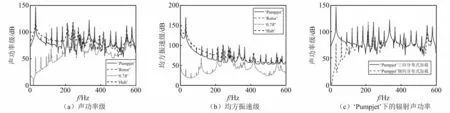
图11 辐射声功率和均方振速Fig.11 Sound radiation power level and mean-square velocity level
给出4个典型频率30.4 Hz(轴频),243.3 Hz(8倍轴频),273.7 Hz(叶频),334.6 Hz(11倍轴频)的声辐射指向性,如图12所示。场点位于水平面内,是以原点为中心直径50 m的圆。轴频处指向性为椭圆,首尾方向的辐射噪声较大;8倍轴频处为蝴蝶形,首尾方向和正横方向的辐射声压较小。除叶频外,其他3个频率处‘Pumpjet’和‘Rotor’基本重合。叶频处各种载荷施加方式的指向性差异较大,这是由于声辐射同时包含了艇体、泵喷转子、泵喷定子和导管的辐射声压,导管本身脉动压力在叶频处较大,也产生直接声辐射,并且和转子、定子等辐射声压叠加,而其他施加方式下导管的振动较小。
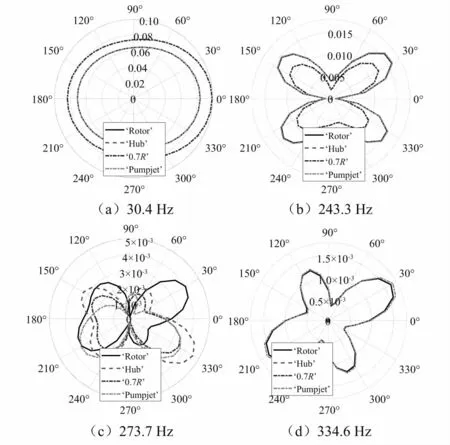
图12 4个频率处的指向性图Fig.12 Sound radiation directivity pattern at four frequencies
为衡量导管和定子上的脉动压力对水下声辐射的贡献,仅将导管和定子上的脉动压力施加到结构网格上,计算辐射声功率级和均方振速级,结果如图13所示。由图13可知,导管和定子上的脉动压力对艇体水下声辐射的主要贡献体现在叶频和2倍叶频处,这是由于导管上的脉动压力在这两个频率处为显著峰值。另一方面,结合图9的模态结果可知,与这两个激励频率接近的结构模态也被激发,出现峰值。分别在整个泵喷推进器表面、只有转子表面、只有导管-定子表面施加脉动激励力,计算得到各自的辐射声功率和均方振速,并进行比较。可知,在单独导管-定子脉动压力激励下,存在一些突出线谱峰值,量级和转子脉动压力激励下的辐射声功率和均方振速量级可比拟,但它们对整体声辐射的贡献可以忽略。在两者同时激励时,均方振速和辐射声功率级并没有显著增大。这是由于在导管-定子和转子脉动压力同时激励下,相位差会导致相互抵消。为验证抵消效应,取出艇体和导管上某监测点的法向速度响应,如图14所示。由图14可知,在整个泵喷推进器脉动压力激励时,法向速度会比导管-定子、转子分别施加脉动压力时小,这表明,同时施加脉动压力会由于相位差相互抵消,不同位置处的相互抵消情况会有所差别。
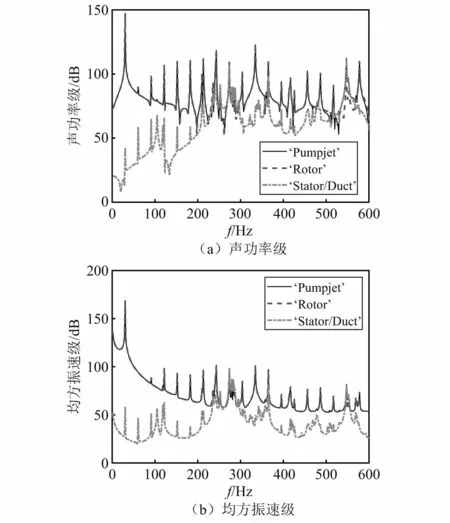
图13 导管-定子、转子分别施加脉动压力时响应Fig.13 SRPand MSV under distributed pressure applied on duct-stator,rotor separately
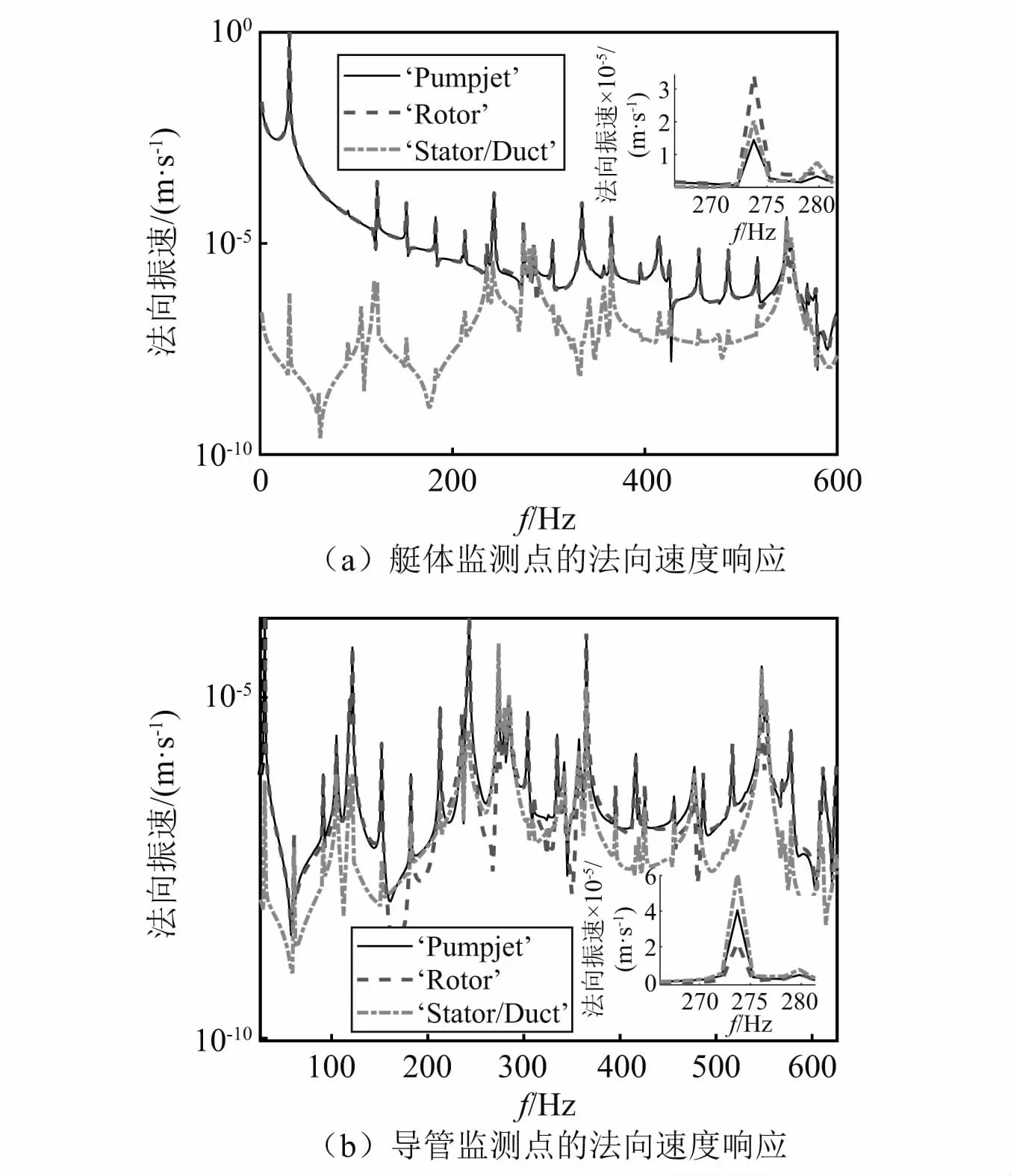
图14 导管-定子、转子分别施加脉动压力时法向振速响应Fig.14 Normal velocity under distributed pressure applied on duct-stator,rotor separately
4 结 论
开展了suboff艇后泵喷推进器脉动压力激励下泵喷-轴系-艇体耦合系统的振动声辐射响应计算和分析。利用CFD模型获得了艇体泵喷推进器的脉动压力。采用耦合有限元法和边界元法获得了分布式脉动压力激励下泵喷-轴系-艇体耦合系统的传递力、声辐射响应。得到结论如下:
(1)泵喷-轴系-艇体耦合系统的振动声辐射以转子脉动压力激励下的响应占主导,而其中2倍轴频以上以纵向脉动压力的贡献占主导。
(2)泵喷-轴系-艇体耦合系统振动声辐射响应中,显著的峰值包含泵喷脉动压力的轴频及其倍频成分(以轴频、叶频最大),也包含轴系一阶纵振和二阶纵振、艇体纵向振动等结构模态。
(3)导管的脉动压力以叶频和2倍叶频为主,导管-定子脉动压力激励下振动声辐射响应峰值出现在上述频率处;且响应量级和转子表面脉动压力激励处于同一量级;但导管-定子、转子表面同时施加脉动压力时,由于相位相互抵消,均方振速和辐射声功率级并没有显著增大。
