一种新颖的TSC无功循环投切装置

孙春虎，方愿捷

（巢湖学院电子工程学院，安徽巢湖238000）

动态无功补偿装置主要包括晶闸管投切电容器（thyristor switching capacitor，TSC）、晶闸管相控电抗器（thyristor phase controlled reactor，TCR）、TSC+TCR、无功功率发生器（reactive power generator，SVG）和有源电力滤波器（active power filter，APF）。其中，TSC补偿装置由于控制简单、运行时无谐波、损耗小的优点而得到广泛应用。文献[1]提出了一种TSC就地动态无功补偿装置，不仅提高了功率因数，还有效减少了谐波。文献[2]提出了一种APF与TSC相结合的混合滤波系统，有效减少了谐波电流，并且系统动态响应快、稳定性好。文献[3]提出了一种TSC与SVG协同运行的混合无功补偿系统，具有大容量TSC无功补偿和SVG动态连续无功补偿的优点，并且能抑制一定程度的不平衡电压。文献[4]提出了一种基于DSP的TSC型动态无功补偿仿真系统，能快速地实现对冲击性负荷的动态无功补偿。文献[5]提出一种基于TSC与磁能恢复开关（magnetic energy recovery switch，MERS）的大容量混合无功补偿系统，TSC实现了多级投切，避免了过电压冲击，MERS实现了无功的连续调节，降低了电流谐波含量。文献[6]提出了一种基于模糊控制的改进型九域图TSC无功补偿控制策略，能快速、精准地完成电容器投切，功率因数高，无投切振荡。但传统的TSC投切装置仍存在以下两个问题：存在“投切振荡”现象与未采用循环投切控制。

针对以上问题，本文基于DSP和PLC，设计了一种新颖的TSC无功投切装置，该装置不仅能实现传统的无功补偿，还能避免“投切振荡”的发生，而且还能实现电容器的循环投切，从而提高了电容器的使用寿命和装置的可靠性。

1 新颖TSC无功投切装置原理

新颖TSC无功投切装置原理框图如图1所示，它主要由三相固态继电器1～6、三相电压电流采样电路、三相电容器1～6、调理电路、FX2N系列PLC电路和DSP2812控制电路组成。

图1 新颖TSC无功投切装置原理框图Fig.1 Block diagram of novel TSC reactive switching device

如图1所示，电压、电流采样电路采样三相电压和三相电流，并通过调理电路送到DSP的A/D采样口；DSP依据采样的三相电压、三相电流计算出瞬时无功功率Q，并通过SCI通信口与FX2N系列PLC进行全双工通信；PLC根据瞬时无功功率Q计算出当前共需要投入电容器的数量，并通过Y端口控制三相固态继电器1～6的控制端；三相固态继电器1～6根据Y端口的控制信号决定6组电容器的投切，以此实现负载瞬时无功功率的补偿。

2 新颖TSC装置控制电路设计

新颖TSC无功补偿装置控制电路包括：三相电压、电流采样电路、调理电路、DSP控制电路和PLC控制电路。这里重点介绍DSP控制电路设计和PLC控制电路设计。

2.1 DSP控制电路设计

为了提高无功功率检测和程序执行的速度，以DSP2812处理器为核心，设计了DSP2812控制电路，图2为DSP控制电路图。如图2所示，三相电压和电流采样信号经调理电路送到DSP的AD⁃CINB0～ADCINB5采样口，接着通过无功功率算法求出瞬时无功功率Q，然后DSP2812与PLC进行RS-232通信，PLC接收的瞬时无功功率Q来自DSP2812的SCITXDB口，DSP的SCIRXDB口接收PLC发送过来的数据[7-8]。

图2 DSP控制电路图Fig.2 DSP control circuit diagram

2.2 PLC控制电路设计

所设计的PLC控制电路如图3所示，它主要用于与DSP2812进行通信，同时控制6路固态继电器的通断，从而实现不同无功功率的补偿以及循环投切控制。

图3 PLC控制电路图Fig.3 PLC control circuit diagram

PLC的引脚TXD用于发送PLC数据；RXD引脚实现无功功率Q的接收，并根据Q计算出当前共需要投入几组电容器；Y0～Y5输出口分别与固态继电器1～6的直流控制端的负端相连；6路固态继电器直流控制端的正端与24 V电源正端相连；24 V电源负端与COM端相连[9-10]。如当Y0导通时，固态继电器1接通，第1组电容器投入运行；当Y0关断时，固态继电器1关断，第1组电容器从电网中切除，不工作。

3 新颖TSC循环投切控制策略

根据TSC投切控制的发展现状，结合各种投切控制策略的优缺点，提出了一种新颖的TSC循环投切控制策略，并进行了理论分析。

3.1 TSC投切控制的发展现状

关于TSC的投切控制策略，文献[8]提出，每组电容器的电容值等容进行补偿，如1：1：1：1的方式，当需要接通几组电容器时，每次都从第1组电容器开始接通补偿，这种方式未采用循环投切方式，容易造成前几组电容器的频繁投切，从而降低了其使用寿命，系统可靠性降低。文献[9]提出，每组电容器的电容值等比例进行补偿，如8∶4∶2∶1的方式，进行无功补偿时，只有唯一的接通方式，无法进行循环投切，而且在负载无功较小时，容量较小的电容器会反复投切，同样会降低系统的可靠性[11-12]。

3.2 循环投切控制方案选择

为了设计循环投切控制方案，文章提出了2种循环投切控制方案。

方案一：每组电容器的电容值等容进行补偿，在投入时，记录每组电容器的投入次数，当下次再次需要投入时，按照投入次数最少的最先投的方式进行投入，直到满足投入需求；同理，在切除时，记录每组电容器的切除次数，当下次再次需要切除时，按照切除次数最少的最先切的方式进行切除，直到满足切除需求。此种方案需要不断累积每组电容器的投入和切除次数，而且还要比较各组电容器的投入和切除次数，编程难度大、工作量大，不易实现。

方案二：每组电容器的电容值仍采用等容进行补偿，以4组电容器为例，当需要投入1组电容器时不能只让固定的1组电容器投入，而是有C14种可能，可以让这4种可能采用循环工作的方式投入运行；同理，当需要投入2组或3组电容器时，应让C24或C34种可能采用循环工作的方式投入运行；而当需要投入0组或4组电容器时，4组电容器需全部关断或接通，控制方式唯一。此种方案解决了无功补偿时各组电容器工作时间和工作频率不同的问题，实现了各组电容器均等工作的目的，提高了系统的可靠性。

综合比较方案一和方案二，方案二的控制方式难度适中、计算量适中，易于实现。为此，文章新颖的TSC循环投切控制方案采用方案二。

3.3 新颖的TSC循环投切控制策略

TSC投切控制策略为：首先，DSP根据采样的三相电压和三相电流计算出瞬时无功功率Q；接着，DSP通过SCI通信口传送瞬时无功功率Q给FX2N系列PLC；然后，PLC根据瞬时无功功率Q的大小确定共需投入几组电容器K，若本次电容器组数等于上次电容器组数，则进入下个循环，若不等则用本次电容器组数值更新电容器组数上次值，并进入K值大小判断程序；最后，根据不同K值出现的次数进行统计，并对每个K值进行循环投切控制。

下面以3组电容器为例，对循环投切控制策略进行介绍。当系统第1次出现K为1时，只让第1组电容器接通；当系统第2次出现K为1时，只让第2组电容器接通；当系统第3次出现K为1时，只让第3组电容器接通；当系统第4次出现K为1时，又只让第1组电容器接通；依次控制规律反复循环接通控制。同理，K为2时，按照第1组、第2组，第2组、第3组，第3组、第1组的循环规律接通电容器。而当K为0或3时，只有唯一的控制方式，那就是3组电容器均不接通或3组电容器全部接通。

下面研究无功功率Q和电容器组数K之间的控制原理和数学关系。

假设系统有3组电容器，每组电容器补偿容量为 10 kvar，则系统可以提供 0 kvar，10 kvar，20 kvar，30 kvar的无功补偿能力。TSC投切装置采用功率因数为控制目标时容易产生“投切振荡”现象，因此，为避免此现象的发生，这里采用无功功率为控制目标，取无功功率误差最小的投法进行投入补偿[13]。

依照无功功率控制法，无功功率Q与投入电容器组数K之间的关系如表1所示。

表1 无功功率Q与投入电容器组数K之间的关系Tab.1 Relation between reactive power Q and number K of input capacitors

由表1可知，此种控制方法的无功功率误差始终在5 kvar的范围内，且不会出现“投切振荡”。

当PLC根据无功功率Q计算出投入电容器组数K后，还要进行循环投切控制，循环投切算法的流程图如图4所示。

图4 循环投切算法流程图Fig.4 Flow chart of cyclic switching algorithm

图4中，系统首先初始化K，K1，m，n值并定时180 s，K为本次电容器组数，K1为上次电容器组数，m，n为变量；当定时时间到时，读取无功功率Q值，利用表1无功功率Q值和电容器组数K之间的数学关系，计算出K，若K=K1，则进入下次循环，从而减少循环投切的次数；若K≠K1，则将K值赋给K1，然后进入判断K值大小程序；若K=0，则3组电容器全切除，进入下次循环；若K=3，则3组电容器全投入，进入下次循环；若K=1，则m先自加1，接着判断m的值，若m=1，则只投入第1组电容器并进入下次循环，若m=2，则只投入第2组电容器并进入下次循环，若m=3，则只投入第3组电容器，对m值清0并进入下次循环；同理，若K=2，则n先自加1，接着判断n的值，若n=1，则只投入第1，2组电容器并进入下次循环，若n=2，则只投入第2，3组电容器并进入下次循环，若n=3，则只投入第3，1组电容器，对n值清0并进入下次循环。

3.4 循环投切算法一般控制规律

假设系统电容器组数为n，系统共检测无功功率Q为m次，其中投入电容器组数K=K1出现h次，那么K≠K1出现次数i为（m-h）次。

4组电容器投入2组的组合形式有第1，2组、第2，3组、第3，4组、第4，1组、第1，3组、第4，2组，共6组，那么n组电容器投入k组的组合数量应为

假设投入k组电容器的次数为ik，那么有：

当投入次数足够多，投入k组电容器时，Ckn个组合中每个组合出现的次数j应为

虽然投入电容器组数K=K1出现了h次，但是这h次投切并未改变投切次数和状态，系统仍采用前一状态。而在K≠K1的i次投切中，当投入次数足够多，在投入任意组数的电容器时，由于投入的每个电容器出现的概率相同，因此，每个电容器投切的次数相同，从而系统每个电容器总的投切次数相同，系统在实现循环投切的同时，提高了使用寿命和可靠性。

4 新颖TSC循环投切相关程序

新颖TSC循环投切控制相关程序主要包括PLC通信程序和PLC循环投切算法控制程序。

4.1 PLC通信程序

PLC的通信程序如图5所示，线圈M8161得电，为8位数据传送模式；通信控制字为H81，波特率为9 600 bit/s，1位停止位，无奇偶校验位，数据位数为8位；RS指令用于接收串口数据，并存储在D10中；当接收标志M8123置1时，将D10数据保存到D11中，并清0接收标志位[14]。

图5 PLC通信程序Fig.5 PLC communication program

4.2 PLC循环投切算法控制程序

PLC循环投切算法流程图如图6所示，当K=K1时，重新计算K值；当K≠K1时，将K值赋予K1，当K值为0～3时，执行相应的循环投切控制，控制结束后返回主程序，开始下次循环。

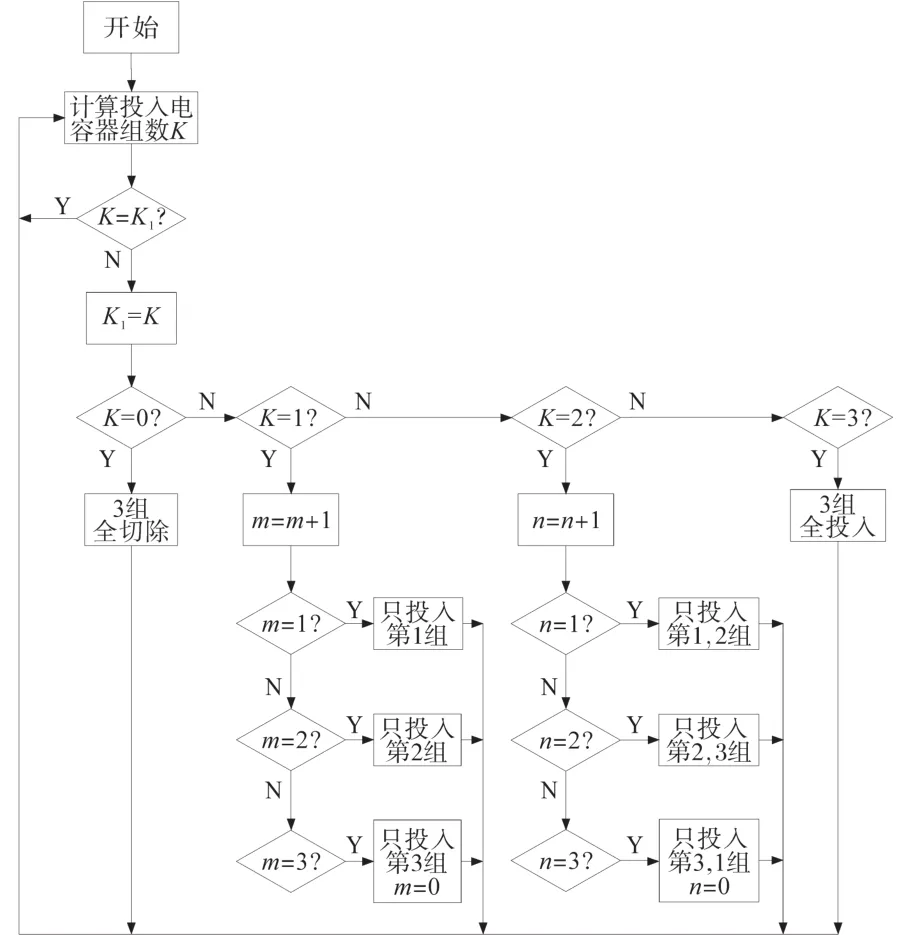
图6 PLC循环投切算法流程图Fig.6 PLC cycle switching algorithm flowchart

循环投切算法主要程序一如图7所示。图7中，D11代表无功功率Q；D20，D21代表变量m和n；D22，D23代表电容器组数K和K1；Y0～Y2为第1，2，3组电容器控制端。FMOV指令用于初始化D20～D23；T0定时器每过180 s执行1次4条ZCP区间比较指令，判断D11处于哪个区间：若处于区间0～5 kvar，则M1接通，投入0组电容器，D22赋值为0；若处于区间6～15 kvar，则M4接通，投入1组电容器，D22赋值为1。

图7 循环投切算法主要程序一Fig.7 The main program one of cyclic switching algorithm

循环投切算法主要程序二如图8所示，当D22值为1时，D20值加1，3条CMP指令用于判定D20值为1、为2还是为3，若为1，则仅Y0为1，只有第1组电容器投入；若为2，则仅Y1为1，只有第2组电容器投入；若为3，则仅Y2为1，只有第3组电容器投入，同时将D20值清0。

图8 循环投切算法主要程序二Fig.8 The main program two of cyclic switching algorithm

5 循环投切控制策略仿真

为了验证控制策略的控制效果，利用三菱编程与仿真软件Gx-works2对控制策略进行了仿真。仿真时无功功率Q由D11赋值给定，同时为了缩短仿真时间，将定时器T0设定值由原先的180 s变为1 s，按照第4.2节的PLC循环投切算法控制程序对循环投切控制策略进行仿真。

5.1 避免投切振荡实验仿真

仿真1：假设有功功率P为20 kW，无功功率Q为9 kvar，每组电容器无功补偿量为10 kvar。

在第4.2节的PLC循环投切算法控制程序的基础上，增加了如图9所示的程序段。

图9 仿真1增加的程序段Fig.9 Additional program segment in simulation one

如图9所示，D11值被赋值为9，表示负载无功为9 kvar；T0设定值由原先的1 800变为10，表示定时时间由180 s变为1 s，从而缩短了仿真时间。而仿真结果为动态的变化过程，为了看到这一过程，可以将仿真结果记录成按时间变化的表格，即可清晰地展现这一过程。程序仿真结果如下：仿真时间t在0～1 s时，K1Y0值为0，1 s之后K1Y0值为1。

由仿真结果可得：1 s之后Y0值为1，表示系统只投入第1组电容器并一直保持，系统功率因数由0.912提高到0.999。虽然出现了过补偿，但是较功率因数控制法，不会出现“投切振荡”现象。

仿真2：假设有功功率P为20 kW，无功功率Q为7 kvar，每组电容器无功补偿量为10 kVar。同理增加了如图10所示的程序段。

图10 仿真2增加的程序段Fig.10 Additional program segment in simulation two

如图10所示，D11值被赋值为7，表示负载无功为7 kvar；T0定时时间为1 s。程序仿真结果为：仿真时间t在0～1 s时，K1Y0值为0，1 s之后K1Y0值为1。

由仿真结果可得：1 s之后Y0为1，系统只投入第1组电容器并一直保持，系统功率因数由0.944提高到0.989。虽然出现了过补偿，但是较功率因数控制法，不会出现“投切振荡”现象。

5.2 当负载无功处于某区间变动时实验仿真

当负载无功处于某一区间变动时，如果仍然采用循环投切，就会造成频繁地投切，增加了投切次数，减少了装置的寿命。如当负载无功在16～25 kvar之间变动时，根据表1，应投入2组电容器，若采用循环投切方式投入2组电容器，就会不停地出现投入第1，2组电容器、投入第2，3组电容器、投入第3，1组电容器的情况。因此，控制策略当检测到这种情况时，则先投入第1，2组电容器，并保持系统状态不变，然后按照出现这种情况的次数进行循环投切。

仿真3：假设有功功率P为50 kW，无功功率Q在0～2 s为 18 kvar，2～4 s为22 kvar，4 s之后为20 kvar，每组电容器无功补偿量为10 kvar。

在第4.2节的PLC循环投切算法控制程序的基础上，增加了如图11所示的程序段。

图11 仿真3增加的程序段Fig.11 Additional program segment in simulation three

如图11所示，无功功率D11值在0～2 s被赋值为18 kvar，在2～4 s被赋值为22 kvar，在4 s之后被赋值为20 kvar；T0定时时间为1 s。程序仿真结果如下：仿真时间t在0～1 s时，K1Y0值为0，1 s之后K1Y0值为3。

由仿真结果可得：1 s之后Y0和Y1均为1，系统只投入第1，2组电容器并一直保持，并没有出现循环投切的情况，从而减少了电容器的投切次数，提高了装置的寿命。

5.3 电容器组数K=1时循环投切仿真

仿真4：假设有功功率P为50 kW，无功功率Q在0 s，2 s，4 s，6 s，8 s，10 s，12 s，14 s，16 s时分别为 0 kvar，6 var，0 var，8 var，0 var，10 var，0 var，12 var，0 var，每组电容器无功补偿量为10 kvar。

在第4.2节的PLC循环投切算法控制程序的基础上，增加了如图12～图14所示的程序段。

图12 仿真4增加的程序段一Fig.12 Additional program segment one in simulation four

图13 仿真4增加的程序段二Fig.13 Additional program segment two in simulation four

图14 仿真4增加的程序段三Fig.14 Additional program segment three in simulation four

如图12所示，D11初始值为0，T0定时1 s。如图13所示，用了8条CMP指令，实现2 s，4 s，6 s，8 s，10 s，12 s，14 s，16 s时的无功功率的重新赋值操作。如图14所示，用了8条MOVP指令，实现2 s，4 s，6 s，8 s，10 s，12 s，14 s，16 s时重新赋值6 var，0 var，8 var，0 var，10 var，0 var，12 var，0 var的操作。

程序仿真结果如表2所示。

由表2可得：2 s时，K1Y0值为1，表示Y0值为1，系统只投入第1组电容器；6 s时，K1Y0值为2，表示Y1值为1，系统只投入第2组电容器；10 s时，K1Y0值为4，表示Y2值为1，系统只投入第3组电容器；14 s时，K1Y0值又为1，表示Y0值为1，系统又只投入第1组电容器。

表2 电容器组数K=1时，K1Y0值随时间的变化关系Tab.2 Change of K1Y0 value with time when the number of capacitor groups is K=1

由此可知，当电容器组数K=1时，无功功率不停在2个区间来回变动时，系统实现了循环投切控制。

6 结论

文章提出了一种新颖的TSC无功补偿装置，并对装置的硬件系统、控制策略和PLC程序进行了设计，最后利用Gx-works2仿真软件对控制策略进行了仿真，仿真结果表明：该无功补偿装置和控制策略既能实现负载的无功补偿，又能避免电容器的“投切振荡”现象的发生，而且实现了电容器的循环投切，提高了电容器的寿命和装置的可靠性，具有一定的实用价值。