基于强化学习的多光储虚拟同步机频率协调控制策略
2021-10-11张华强牟晨东赵玫姚统
张华强,牟晨东,赵玫,姚统
(哈尔滨工业大学(威海)新能源学院,山东威海264209)
目前,大量的光伏电源采用PQ控制方式接入到微电网,由于其缺乏传统同步发电机的转动惯量,导致微电网应对功率扰动的能力较差,同时光伏电源不能自主参与微电网的电压、频率调节过程,使得微电网运行的稳定性受到了很大挑战[1-3]。
为了从源头解决这些问题,众多学者借鉴传统同步发电机的转子运动方程、调速器以及励磁器原理,将虚拟同步机(virtual synchronous genera⁃tor,VSG)技术引入逆变器控制策略中[4],使得分布式电源能提供惯性响应以及自主参与微电网调频。传统的分布式光伏电源由于不配备储能装置,在微电网的频率控制与功率调度中通常将其作为不可控电源进行处理。随着储能装置的不断发展以及VSG技术在光伏发电领域的不断应用,光伏电源可通过配备储能装置实现由不可控电源向可控电源的转变。文献[5]对采用下垂与虚拟惯量控制的光伏电源参与电网频率调整的机电暂态过程进行了详细分析,光伏电源做减载运行,进而具有有功备用;文献[6]在文献[5]的基础上提出了多光伏电源参与系统频率调节的协调控制策略,验证了多光伏电源参与频率调整的可行性与有效性;文献[7-8]通过为光伏电源配备储能的方式将其视为可控电源,光储发电系统可以根据微电网的频率控制与调度需求输出指定功率。以上文献将光储发电系统的发电运行成本拟合成关于输出功率的多项式形式,可定量计算光储的发电成本,为本文实现多光储VSG频率协调控制提供了理论基础。
由于VSG一次调频属于有差调频,为了保证微电网供电的电能质量,需对微电网的频率进行二次调整[9]。文献[10]结合集中式与分散式频率调控的优点,通过定义最大出力因子实现各电源按照发电容量输出功率进行二次调频,但其没有考虑各发电单元的发电成本,不利于微电网经济运行。文献[11]讨论了微电网频率集中控制的可行性,中央控制器按照一定的规则对计划外的负荷进行再分配,但其计划外负荷的计算仍然采用积分控制,存在相关参数难以整定以及与微电网具体环境联系较大的问题,一旦微电网结构发生变化,其控制参数需要进行相应的调整,通用性较差。
为了解决以上问题,基于强化学习的控制策略不断得到应用。文献[12]将强化学习策略应用至风储合作决策过程中,在缓解电网调控压力的同时提高风储合作的效率。文献[13]针对下垂控制存在频率与电压误差的问题,利用强化学习算法中的Q学习实现分布式频率与电压二次优化控制。文献[14]针对传统的PI控制参数整定困难以及结构拓展性差的问题,提出了一种基于Q学习的微电网频率自适应控制策略。
本文在此基础上,借鉴文献[15]的两级控制方式,提出了多光储虚拟同步机的频率协调控制策略。以光储虚拟同步机为研究对象,在光伏电源直流侧配备储能装置使其在一定程度上成为可调度单元;上层中央控制器实时检测系统的频率,采用强化学习控制策略根据以往决策历史与经验计算功率缺额,然后按照各光储电源的发电运行成本利用拉格朗日乘子法进行功率分配,动态调整各光储VSG的输出功率,实现多光储虚拟同步机的频率协调控制。
1 光储虚拟同步机控制策略
图1所示为光储VSG的电路结构。光伏电源与储能装置通过DC/DC电路与直流母线相连。通常情况下光伏电源处于MPPT状态下,储能装置维持直流母线电压恒定,逆变器采用VSG控制策略,储能装置负责提供光储VSG所需的惯性响应以及调频所需的能量,同时应对光伏的出力波动。
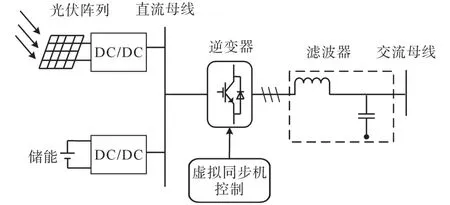
图1 光储VSG电路结构Fig.1 Structure of PV-BA VSG
1.1 VSG控制策略
VSG控制主要包括有功—频率(P—f)控制器以及无功—电压(Q—U)控制器。P—f控制器主要根据发电机转子方程建立,其表达式如下:

式中:J为虚拟转动惯量;D为阻尼系数;PT,Pe为输入机械功率与VSG输出功率;ωn,ω为额定角频率与角频率。
为使VSG能自主参与微电网的频率调整,借鉴同步机调速器原理,其输入的虚拟机械功率表达式为

式中:Pset为VSG有功功率设定值;kf为VSG频率调差系数。
通过式(1)、式(2)可知VSG稳态时输出功率为
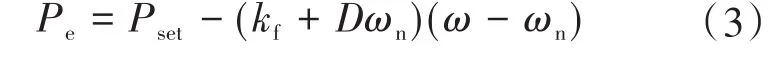
VSG的输出电势eabc为
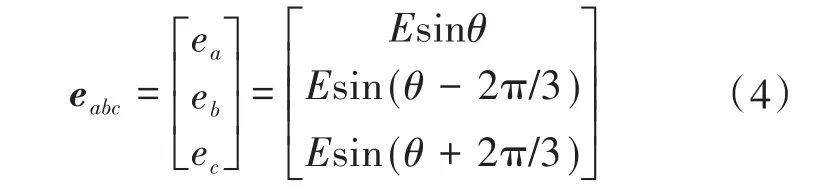
其中

式中:θ为输出电压的虚拟相角,可由虚拟角速度ω积分得到;E为电势幅值,可由Q—U控制器得到;Qset为无功功率设定值;Q为无功功率;E0为VSG虚拟空载电压;δ为电压调差系数。
本文重点研究光储VSG的频率控制,电压控制部分不做详尽分析。VSG控制策略如图2所示。
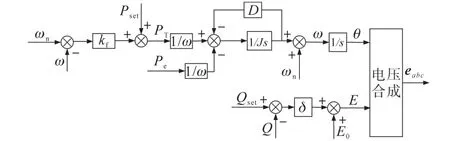
图2 VSG控制框图Fig.2 Control block diagram of VSG
由于微电网的线路阻抗呈现阻感性,导致逆变器输出的有功功率与无功功率存在耦合,不利于逆变器的功率控制与参数整定。本文在逆变器底层控制中加入虚拟电感,使得逆变器等效输出阻抗呈感性,实现有功功率与无功功率的解耦。
1.2 光储VSG直流侧控制策略
光储VSG直流侧控制主要包括光伏与储能控制。光伏电源采用双级式电路结构,通过Boost电路实现光伏的最大功率追踪,其控制策略采用电压电流双闭环控制方式,电压环参考电压通常为光伏电源最大功率点所对应的直流电压。
为实现光储VSG,可根据微电网调度需求输出指定功率,储能装置需要根据光伏电源的出力与调度指令进行充电或放电,用以弥补光伏电源以及逆变器输出的功率差额。储能装置可通过双向DC/DC电路(Buck-Boost)与直流母线连接,其控制方式如图3所示。

图3 储能装置控制策略Fig.3 Energy storage device control strategy
为增强光储VSG的可调度性,当储能电池可用充电容量较小而光伏电源的最大输出功率大于微电网的功率调度指令时,此时光伏应运行在减载状态,需要附加额外的控制,其具体控制方式参考文献[16]。
2 多光储VSG频率控制策略
2.1 单台光储VSG频率调节原理
若微电网频率处于额定频率,当微电网发生功率波动时,光储VSG会自主参与系统一次调频,VSG输出频率与负荷变化ΔPload的关系为
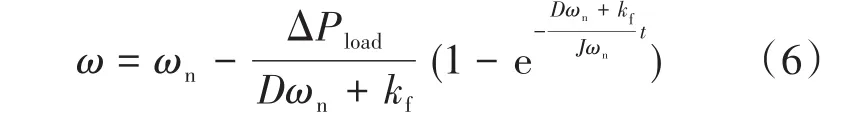
当系统的负荷波动较大,一次调频后系统频率不能够满足系统频率的要求,同时为了保证微电网供电的电能质量,需要进行二次调频。图4所示为VSG二次调频示意图。

图4 VSG二次调频示意图Fig.4 Secondary frequency regulation of VSG
若光储VSG功率设定值为Pset1,微电网负荷为PL1,两直线交于a点,系统的频率为额定值。假定负荷不参与频率调节,当负荷变至PL2时,由于VSG具备一次调频,微电网频率下降至f1。若光储VSG功率设定值抬升至Pset2,频率调节系数保持不变,VSG的P—f曲线斜率保持不变,此时与负荷曲线交至c点,系统频率恢复至额定值。所以光储VSG可以通过改变功率给定值Pset来进行二次调频,不需要添加额外控制。通过图4可知,当只有单台VSG进行二次调频时,其功率设定值应为
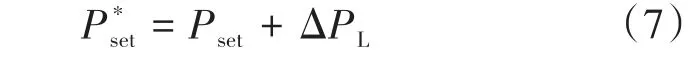
式中:P*set为二次调频后的功率设定值;Pset为调整前的功率设定值;ΔPL为负荷波动值。
2.2 多光储VSG频率协调控制
传统电力系统通常有负责二次调频的调频厂,但微电网情况与电力系统不同的是单个VSG的容量相对较小,仅靠单台VSG不能满足系统频率调整的需求,会造成单台VSG过载而其他VSG的调频能力没有最大限度地利用,所以微电网中需要多台光储VSG共同承担调频任务。
根据式(7)可知,当多台光储VSG参与频率调整时需要满足以下条件:
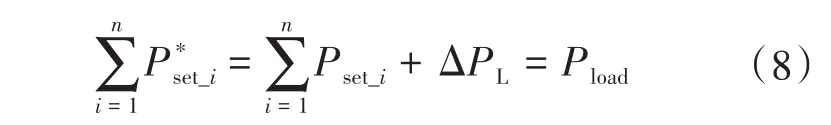
式中:n为参与二次调频的光储VSG个数。
通过分析可知,多光储VSG频率协调控制的本质是多光储VSG功率协调分配问题。
为了保证微电网运行的经济性,需要按照各光储电源的发电运行成本实现多光储VSG功率协调分配。光储电源的运行成本主要由光伏电池板与储能电池维护、置换成本等费用组成,根据文献[17]可知,光储发电成本可拟合成如下式所示的函数形式:
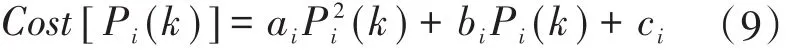
式中:ai,bi,ci为电源 i的拟合运行成本系数。
根据式(9)可知,光储电源与传统火电机组的发电运行成本函数形式相同,所以可以借鉴等耗量微增率的概念对负荷进行经济性的分配。根据拉格朗日乘子法可知,在不考虑功率约束的情况下,当各光储VSG的功率给定值P*set对应边际成本相等时,此时负荷分配方案是最经济的,其边际成本的表达式为

据此,中央控制器计算各光储VSG的最优功率给定值的流程如下:
1)中央控制器根据系统频率计算功率波动值ΔPload;调取各光储VSG的功率极限值,设定边际成本初值ξ0与边际成本更新步长Δξ;
2)根据边际成本值ξ按照式(10)求取对应的各VSG功率设定值,若对应的功率值越界则取上界或下界i;
3)计算调频机组功率设定调节值是否满足等式约束,如下式:
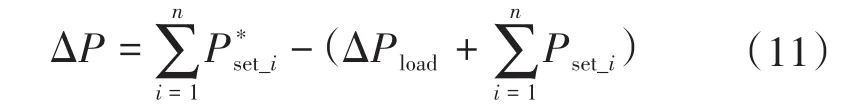
4)不断更新边际成本ξ,直至满足步骤3)的约束条件,输出最终的功率设定值P*set_i。
3 基于强化学习的多光储VSG频率控制
随着通讯技术的不断发展,信息传输的容量、速度以及准确性都有了很大的提升,微电网采用集中式控制的优点逐渐显现。通过第2节的分析可知,多光储VSG频率协调控制的关键是如何计算得到微电网内的功率缺额。传统集中式控制方法通常是中央控制器采集频率偏差通过PI控制器计算出频率积差,但存在PI参数整定困难的缺点,当微电网的结构发生变化时其参数需重新整定,而且不能充分利用以往的决策历史,缺乏一定的智能性。
为了摆脱控制器对于微电网具体结构的依赖以及充分利用以往调控的经验与教训,本文采用基于强化学习(reinforcement learning,RL)的多光储VSG频率协调控制策略。
3.1 Q学习的基本原理
在RL中,智能体(Agent)会根据环境(Envi⁃ronment)当前的状态、以往的学习经验与学习策略执行某个动作,当环境执行完该动作后将反馈信号送回智能体,智能体按照学习目标对刚执行的动作进行评价,根据评价结果确定今后执行该动作的概率增加或减少。
在RL算法的决策算法中,Q学习作为一种无模型学习算法被广泛应用。Q学习是基于值函数的强化学习算法,利用Q值来衡量智能体在状态st下执行动作a的好坏。
Q学习算法根据以往的决策经验与教训建立Q值表,Q值表为一个n×m的矩阵。m为系统动作集A的离散区间个数;n为系统状态集S的离散区间个数。Q值表中Q值更新规则表达式为[13]
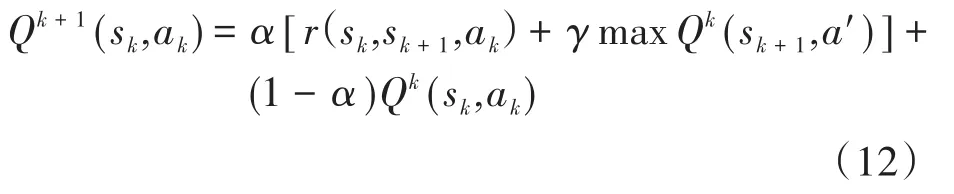
式中:sk,sk+1为当前环境状态与执行完动作ak后的环境状态;r(sk,sk+1,ak)为智能体执行动作ak的奖励值;α为学习因子;γ为折扣因子;a'为状态sk+1下的所有可能动作值;Q(sk,ak)为在状态sk执行ak的值函数。
在Q学习的学习过程中根据状态sk选择动作ak的策略为学习策略,本文采用ε-greedy学习策略,其表达式为

式中:ε为贪婪值,其取值为0~1之间,当其值较大时表明学习策略更倾向于按照最大Q值选择动作;δ为0~1之间随机数;argmaxQ(s,a)为Q(s,a)最大时的动作取值;arand为随机选择的动作值。
在满足某些条件下通过随机选择动作值可以在一定程度上防止Q学习算法陷入局部最优。
Q学习算法在进行决策时只涉及本时刻状态以及下一状态对应的Q值,同时在进行Q值更新时只更新Q(sk,ak),Q值表中其它的状态-动作对均保持原值不变,其计算量不是很大,不会过多增加控制器的计算量以及控制成本。
3.2 Q学习参数设计
通过以上分析可知,Q学习参数主要包括输入状态集S、输出动作集A以及奖励函数R。中央控制器通过检测微电网的频率偏差Δf,根据以往的决策经验估计二次调频功率,所以状态量为微电网频率偏差Δf,动作量为功率缺额ΔP。
状态集S与动作集A均是有限的非空集合,微电网频差Δf可以根据系统的调频需求划分为一定的离散区间。本文二次频率调整目标为(50±0.005)Hz,设计状态集S的离散区间为{(-∞,-0.1),[-0.1,-0.08),[-0.08,-0.05),[-0.05,-0.02),[-0.02,-0.005),[-0.005,0.005),[0.005,0.02),[0.02,0.05),[0.05,0.08),[0.08,0.1),[0.1,+∞)},其对应的状态集S为{s1,s2,…,s11}。
为了增强Q学习动作集的通用性,动作集A中的元素选取为功率标幺值,基准值选取当前微电网最大可调功率[13-14]。当微电网可调功率发生变化时,仅改变功率基准值即可,无需改变动作集A。本文设计的动作集为{-1,-0.6,-0.3,-0.1,-0.08,-0.06,-0.04,-0.03,-0.02,-0.015,-0.01,-0.005,0,0.005,0.01,0.015,0.02,0.03,0.04,0.06,0.08,0.1,0.3,0.6,1},其对应动作集为{a1,a2,…,a25}。
值得注意的是,当动作集与状态集元素个数较多时,其控制精度较高。但由于Q值表维度过高,算法的收敛速度会变慢,所以在进行参数设计时需要统筹考虑控制精度与决策速度。
本文选取奖励函数R为[13-14]

其中,rf(s)为频率奖励函数,其表达式为
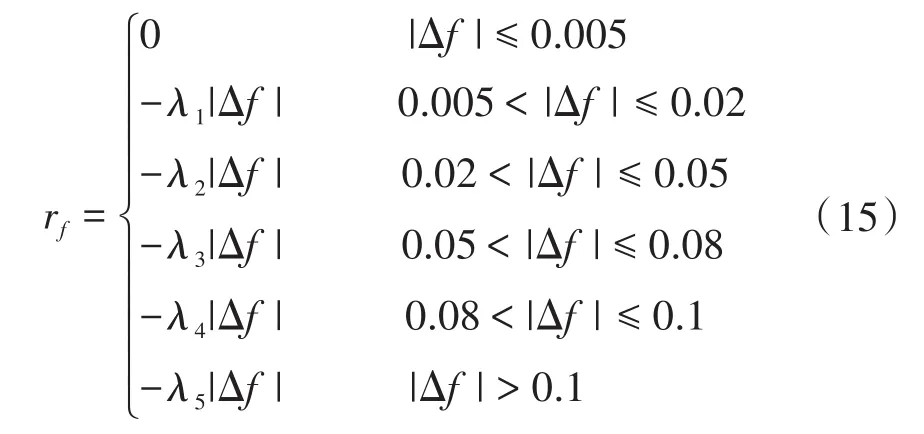
式中:λ1~λ5为频率奖励系数,本文选为 10,20,30,40,50。
为了防止在频率调节过程中造成微电网电压发生越界,所以在奖励函数R中加入电压惩罚项ru(s),其表达式为
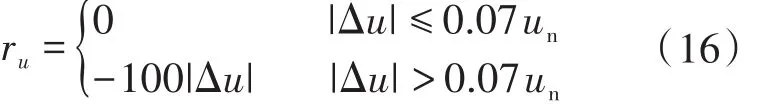
式中:Δu为微电网重要节点的电压偏差;un为该节点的额定电压。
3.3 基于Q学习的频率调节流程
将Q学习的状态集、动作集以及奖励函数设计完之后,基于Q学习的频率控制器还应该进行离线的预学习,通过不断的试错与探索,预学习之后的Q值表便可以应用到实际的微电网频率控制中,本文不再详细叙述。
基于Q学习的频率调节流程如图5所示,其具体频率控制流程如下:
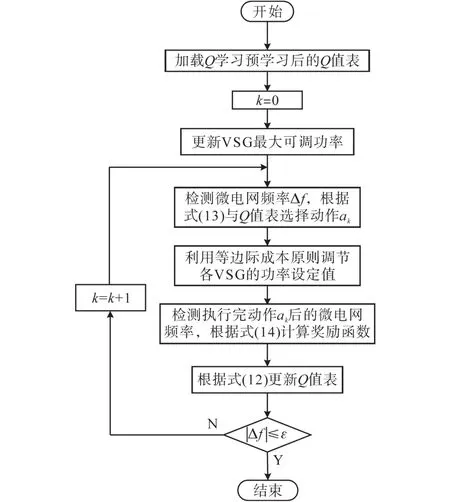
图5 基于Q学习的频率控制流程图Fig.5 Frequency control based on Q-learning
1)检测微电网当前频率偏差,中央控制器根据ε-greedy学习策略选择动作ak(ΔPLk);
2)利用等边际成本原则对各光储VSG有功功率设定值进行调整;
3)检测下一时刻的频率偏差,计算执行动作ak(ΔPLk)的奖励函数值;
4)根据式(12)更新Q值表;
5)判断频率偏差是否满足频率调整目标,不满足二次频率调整目标则返回至步骤1),否则Q学习的学习过程结束。
4 仿真分析
4.1 仿真平台搭建
本文利用Matlab/Simulink搭建的光伏微网结构如图6所示,控制器利用S-function函数进行编写,系统中有4组光伏电源。分布式光储电源发电运行成本系数如表1所示,微电网系统参数以及光储VSG控制参数如表2所示,Q学习奖励函数R中电压惩罚项选取负载4的节点电压值。
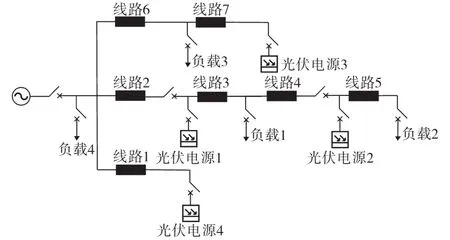
图6 微电网仿真模型结构Fig.6 Microgrid simulation model structure

表1 光储成本系数Tab.1 Cost coefficient of PV-BA

表2 微网与VSG控制参数Tab.2 Microgrid and VSG control parameters
4.2 仿真结果分析
0 s时微电网处于孤岛状态,根据光储VSG光照强度、温度以及储能装置的SOC状态,各PV-VSG的最大输出功率分别为:30 kW,15 kW,20 kW以及15 kW,微电网内的4个负荷分别为8 kW,13 kW,9 kW以及10 kW。VSG1~VSG4的有功功率设定值分别为:12.9 kW,9.1 kW,10.1 kW以及7.9 kW。在1 s时负荷4由10 kW变化为15 kW,1.2 s时投入基于Q学习(已完成预学习)的二次频率控制策略,中央处理器每0.2 s采集1次微电网频率。
图7所示为采用Q学习与PI控制时的微电网频率仿真结果,通过分析可知,当采用Q学习后微电网频率可以快速恢复,而且不需要复杂的控制参数调试。图8所示为采用Q学习控制策略时光储VSG输出功率。

图7 微电网频率Fig.7 Microgrid frequency

图8 VSG输出功率Fig.8 Output power of VSG
通过图7可知,在1 s之前虽然各VSG的有功功率给定值之和等于负荷总和,但由于微电网电压等级较低,线路阻抗中电阻分量较大,微电网中有功损耗较大,所以各VSG的输出功率均略大于给定值,造成微电网的频率略低于额定值,侧面证明了VSG一次调频属于有差调频。
在1 s时负荷突增5 kW,各光伏电源逆变器均采用VSG控制策略,具备一次调频功能,各光伏电源频率调差系数相同,突增的负荷由各光储VSG均摊。微电网的频率大幅度下降。在1.2 s时触发本文所设计的二次调频策略。中央控制器在各时刻检测的微电网频率偏差以及输出动作选择情况如图9所示。
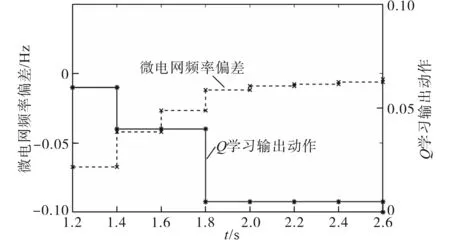
图9 Q学习数据Fig.9 Data of Q-learning
通过图9可知,在1.2 s时中央控制器检测微电网的频率偏差为-0.067 4 Hz,根据Q值表采用ε-greedy学习策略选取动作0.06,此时微电网最大可调度功率为40 kW,中央控制器根据等边际成本原则对各VSG的有功功率设定值进行动态调整,VSG1~VSG4的有功功率设定值调整为:13.7 kW,9.6 kW,10.6 kW以及8.5 kW。0.2 s后(1.4 s)中央控制器再次检测微电网频率偏差为-0.042 1 Hz,并根据式(14)对刚才的动作选择情况进行评价,同时根据式(12)对Q值表中的Q(s3,a20)进行更新,然后根据检测到的频率差值按照ε-greedy学习策略再次选择动作,输出功率缺额,各VSG继续动态调整有功功率给定值,直至系统频率偏差满足调频目标。通过图9可知,在2.6 s时系统频率偏差为-0.004 Hz,满足二次频率调整的目标,频率调整结束。通过仿真结果可知,Q学习通过7次学习完成了频率的二次调节,同时保证了微电网的经济运行,实现了多光储VSG的频率协调控制。
5 结论
为解决光伏发电控制方式缺乏转动惯性以及集中式PI控制方式存在参数难以整定等问题,本文提出了基于强化学习算法的多光储VSG的频率协调控制策略。光储发电底层控制采用VSG控制技术,使得光储具备惯性响应以及调频能力;中央控制器采用强化学习算法根据频率偏差量在线计算微电网的功率缺额,不依赖具体的微电网网架结构与电源分布情况,具备良好的通用性,同时在Q学习的奖励函数R中加入电压惩罚项,防止在频率调整过程中造成电压发生越界;为保证频率调整过程中的经济性,中央控制器依据在线计算出的功率缺额根据等边际成本原则动态调整各VSG的有功功率给定值,实现多光储VSG的频率协调二次控制。仿真结果表明,基于强化学习的频率控制相比于传统的控制策略具备较好的频率调控作用。
