基于双参考系的感应电机模型预测转矩控制

杨鹏，廖晓群，江元，张勇红，侯应龙

（1.国网甘肃省电力公司，甘肃兰州730050；

2.西安科技大学通信与信息工程学院，陕西西安710054）

电力驱动系统的有限集模型预测控制以其概念直观、结构简单、易于处理非线性约束以及动态响应快等优点，近年来得到了学者们的广泛关注[1-3]。针对感应电机驱动系统，有限集模型预测控制可分为模型预测电流控制（model predic⁃tive current control，MPCC）和模型预测转矩控制（model predictive torque control，MPTC）[4-6]。相比于传统的直接转矩控制（direct torque control，DTC），模型预测转矩控制具有较快的电磁转矩响应和较小的电磁转矩脉动。然而，模型预测转矩控制主要有两个缺点[7-10]：1）模型预测控制依赖于感应电机的参数，而定子电阻随着温度的变化而变化，励磁电感随着磁路的饱和而变化。不匹配的电机参数将引起预测误差，进而引起控制性能的下降，甚至系统失稳；2）在电磁转矩预测模型中含有感应电机的转子速度变量，然而转速的测量不可避免地引入了噪声，进而降低了电磁转矩的预测精度。对于无速度传感器的感应电机模型预测转矩控制，经典的转速估计多基于自适应观测器的方法，在该方法中，速度的估计误差、定子磁链的观测误差以及电磁转矩的预测误差，三者相互耦合相互影响，进而降低了感应电机的控制性能。

感应电机的自适应观测器主要包括龙贝格（Luenberger）观测器、卡尔曼滤波器以及滑模观测器等[11-14]。在上述三种自适应观测器中，转速计算作为自适应观测器的最后阶段，容易受到噪声影响，带有估计误差的转速反馈至定子磁链计算模块，又进一步恶化了定子磁链的观测准确度。文献[15]在基于电压模型计算定子磁链矢量的基础上，提出了一种补偿策略，提高了感应电机转速的计算精度。文献[16]提出了一种基于滑模理论的定子磁链观测器，提高了定子磁链观测器的鲁棒性。

针对基于速度自适应观测器感应电机驱动系统的缺点以及电磁转矩预测模型依赖于转速的问题，本文提出了一种基于双坐标系观测器的感应电机无速度传感器预测转矩控制。首先，对于磁链观测和转速估计，采样双参考系的方法，基于电压模型的磁链计算表示在定子坐标系，基于电流模型的磁链计算表示在转子磁链矢量坐标系。上述双坐标系的表示方法可分离定子磁链观测和转速估计的相互影响。其次，在电磁转矩预测模型中，采用基于定子磁链和转子磁链叉乘的数学公式，同时基于转子磁链矢量坐标系表示转子磁链，进一步简化了电磁转矩的预测方程，提高了感应电机电磁转矩的预测精度。最后，提出的双参考系预测转矩控制算法在2.2 kW感应电机实验平台上得到了实验验证。

1 数学模型

在感应电机定子坐标系，三相感应电机数学模型如下式所示[3]：

式中：Ψs，Ψr分别为定子磁链矢量和转子磁链矢量；vs为定子电压矢量；is，ir分别为定子电流矢量和转子电流矢量；Ls，Lr，Lm分别为定子自感、转子自感、定转子互感；Rs，Rr分别为定子电阻和转子电阻；pn为感应电机的极对数；ωr为感应电机的转速；Te为感应电机电磁转矩。

感应电机驱动系统如图1所示，三相感应电机由两电平电压源逆变器（voltage source inverter，VSI）供电。两电平电压源逆变器包含6个绝缘栅双极型晶体管（insulated gate bipolar transis⁃tor，IGBT）。电压源逆变器的开关状态矢量S如下式所示：

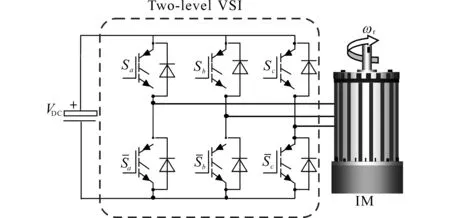
图1 感应电机驱动系统Fig.1 Induction motor drive system

其中

Sa=1表示Sa晶体管处于开通状态，而Sˉa表示其处于关断状态；Sb，Sc同理。

依据电压源逆变器的开关状态矢量，定子电压矢量vs可以表示为

式中：VDC为直流母线电压。

2 基于新型双坐标系观测器的感应电机预测转矩控制

2.1 新型双坐标系观测器

2.1.1 传统的自适应观测器

联立感应电机的状态方程式（1）～式（4），消去定子电流矢量is和转子电流矢量ir，可得到以定子磁链矢量Ψs和转子磁链矢量Ψr为状态变量的感应电机状态方程，如下式所示：

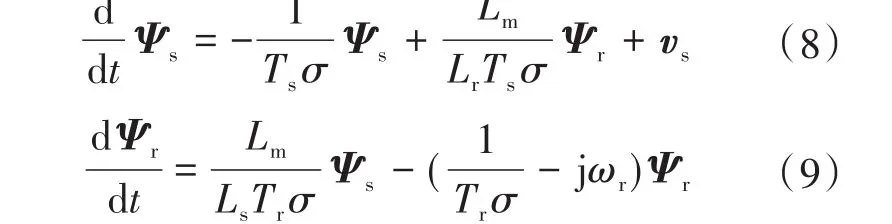
其中

依据线性控制理论，磁链观测器可设计为

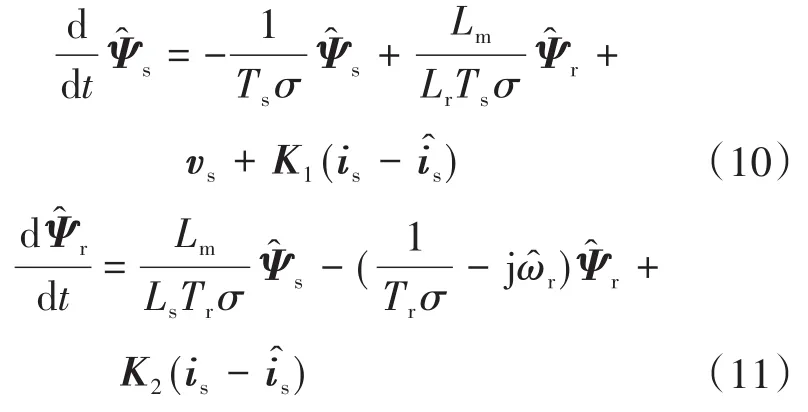
式中：“^”表示观测量；K1，K2为观测器的校正项增益矩阵。

定子电流观测量îs由下式计算：

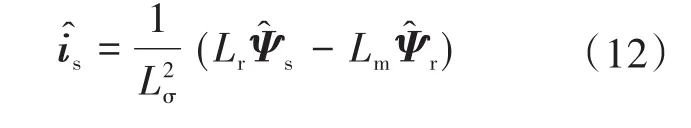
其中

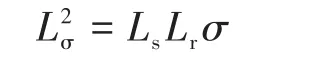
合理设计增益矩阵K1，K2可保证磁链观测器的稳定性。依据线性控制理论的极点配置方法，增益矩阵K1，K2的设计可有多种方案。文献[5]中K1，K2的表达式如下式所示：

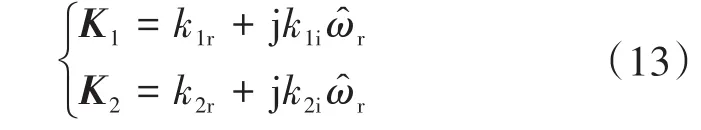
式中：k1r，k1i，k2r，k2i为常数。

基于线性控制理论及Matlab工具软件可绘制感应电机和磁链观测器的根轨迹图，如图2所示。从图中可看出，在高速段，磁链观测器的极点位于电机极点左侧，而随着感应电机转速的降低，两者极点的距离不断减小，此时磁链观测器的动态性能及稳态性能变差。

图2 感应电机与龙贝格观测器的根轨迹图Fig.2 Root locus of induction motor and observer

由于式（11）和式（13）中都含有感应电机转子速度变量ω̂r，而转速的估计一般采用模型参考自适应方法（model reference adaptive system，MRAS），实际电机作为参考模型，磁链观测器作为自适应模型。依据李雅普洛夫稳定性理论推导出转速的自适应机制，如下式所示：

从上述推导可知，定子磁链和转子磁链的估计依赖于感应电机的转速变量。当感应电机的转速动态变化时，转速的估计与磁链的观测相互影响，进一步降低了两者的估计精度。

2.1.2 双坐标观测器

为了消除磁链观测与转速估计的相互耦合，在新型双坐标观测器中，式（8）仍在定子坐标系表示，由于 Ψr=(LrΨ̂s-L2σis)/Lm，方程可简化为dΨs/dt=-Rsis+vs；式（9）由定子坐标系变换到转子磁链矢量坐标系，如下式：

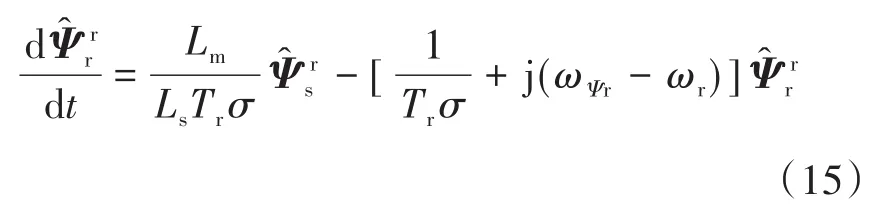
其中

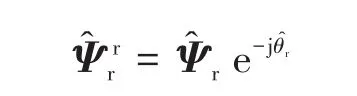
式中：ωΨr为转子磁链矢量的旋转速度；为转子磁链矢量的变换公式；̂为转子磁链矢量角；其余状态变量的变换公式与类同。依据磁场定向的基本原理，在转子磁链矢量坐标系中，转子磁链矢量虚部为零，即=0，那么；因此，式（15）的实部不含有ωΨr和ωr，式（15）可进一步简化为

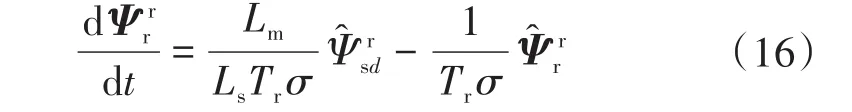
为提高磁链观测的鲁棒性，新型双坐标观测器引入滑模理论，基于滑模切换函数作为校正项，因此双坐标系观测器方程如下式所示：

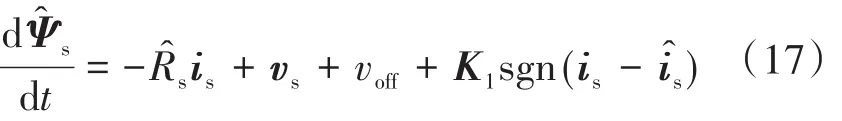
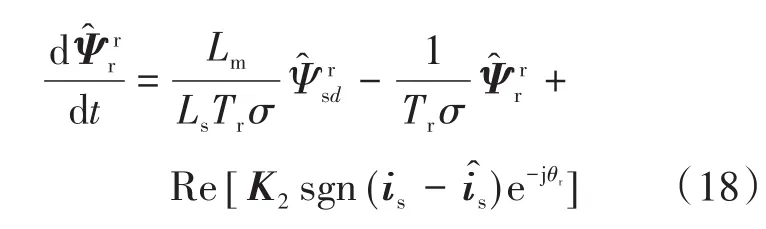
其中，voff为定子磁链模型的补偿项，设计如下式所示：

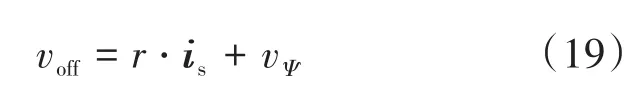
其中，r为电压源逆变器的开关电阻；vΨ为定子磁链误差的补偿项，vΨ的计算如下式所示：

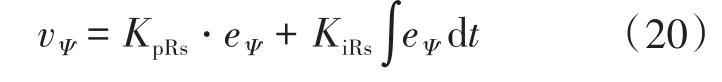
其中

式中：KpRs，KiRs为比例积分系数。

定子磁链模型补偿项框图如图3所示。从上述方程中可以看出，式（17）、式（18）中不含转速信息，消除了转速估计与磁链观测的相互影响。依据感应电机转子转速、转子磁场转速、滑差转速三者之间的关系，转子转速可由定子磁链和转子磁链直接计算得到，如下式所示：

图3 补偿电压计算框图Fig.3 Calculation block diagram of compensation voltage

通过式（21）直接计算转速，提高了转速估计的动态响应。

在观测器方程式（17）、式（18）和转速计算方程式（21）中，含有定子电阻Rs和转子电阻Rr。定、转子电阻随温度的改变而变化，影响磁链与转速的估计精度。在此，假定定子电阻和转子电阻的变化率相同，定、转子电阻的估计方程如下式所示：

式中：krr为调整定转子电阻比率的常系数；KRs为电阻估计的积分系数；irs，îrs为定子电流的采样值和估计值。

本文提出的新型双坐标系观测器框图如图4所示。

图4 新型双坐标系观测器Fig.4 Novel dual reference frame observer

2.2 新型双坐标系转矩预测模型

在传统的感应电机预测转矩控制中，预测转矩模型一般基于定子坐标系，如下式所示[4]：

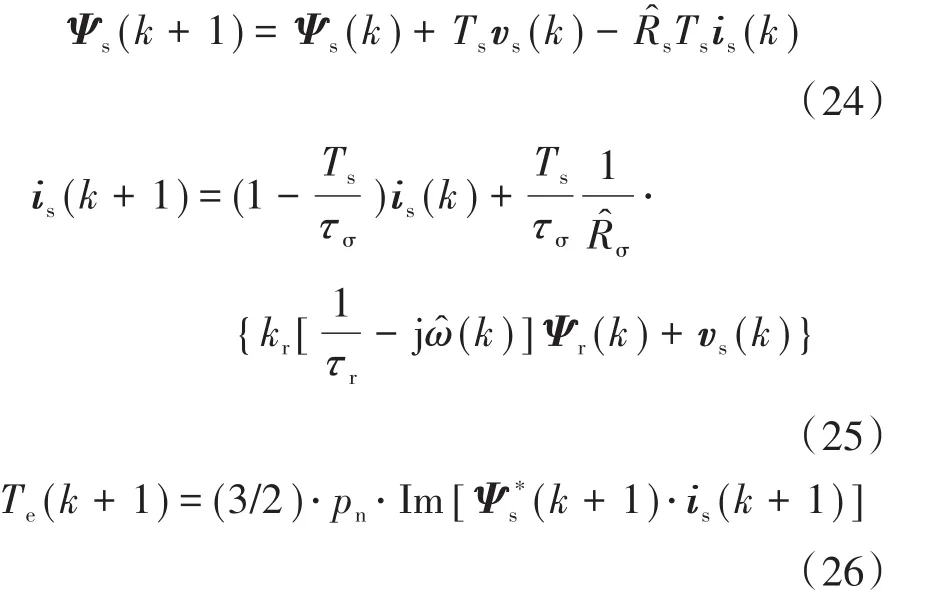
其中

式（25）中含有估计转速项，估计转速的误差会降低预测转矩的精度。

为了提高电磁转矩预测精度，式（25）由式（16）代替，离散化后可得：

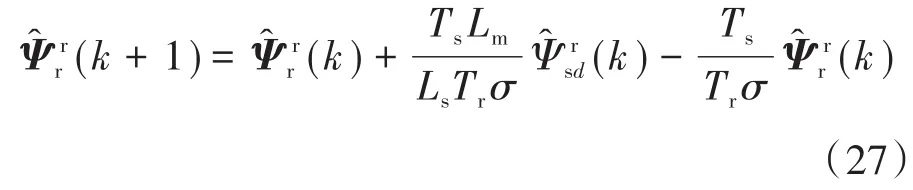
其中，Ψ̂rsd(k)，Ψ̂rr(k)取自上文提出的新型双坐标系观测器，从而消除了感应电机的转速信息。同样地，为提高定子磁链的预测精度，预测方程加入电压补偿，如下式：

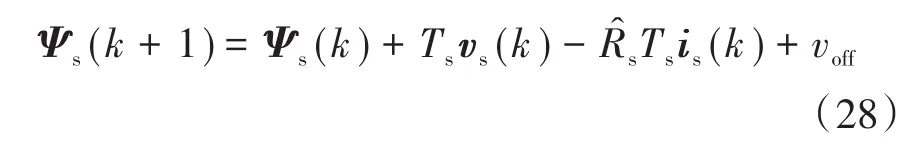
电磁转矩则由定子磁链和转子磁链计算得到，如下式所示：

2.3 代价函数设计

由于代价函数可灵活设计，使得有限控制集模型预测控制成为电力电子及电力驱动领域的研究热点。代价函数可包含参考值跟踪、开关频率限制、过电流保护及频谱含量优化等项。预测控制的代价函数如下式所示：

其中

式中：T*e为电磁转矩参考值；λ为电磁转矩与定子磁链幅值之间的权重系数；Im(k+h)j为过电流保护。

当预测电流|is(k+h)|超过最大值ismax时，Im(k+h)j取值为无穷大，从而舍弃此电压矢量。

对于两电平电压型逆变器，如图5所示，共有6个非零矢量和2个零矢量，2个零矢量只需预测1次，因此，评价函数需计算7次，即j=0,…,6。

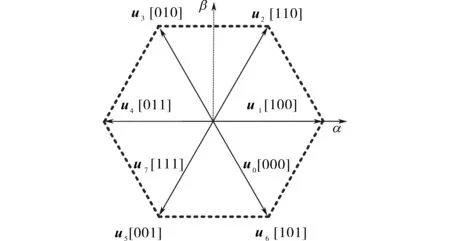
图5 两电平逆变器产生的电压矢量Fig.5 Voltage vector generated by two-level inverter

在数字控制系统中，由于数字处理器执行预测算法需要时间，因此，存在1个控制周期的时间延迟。当前k时刻作用的电压矢量只能在（k+1）时刻施加。为了消除数字控制系统的时间延迟，本文采用“观测器+预测”的方法消除时间延迟，即观测器采用向前欧拉公式，然后在观测器估计（k+1）时刻感应电机状态变量的基础上，预测（k+2）时刻感应电机的定子磁链幅值和电磁转矩。然后，依据预测值及评价函数，选择最优的电压矢量。

感应电机双坐标系预测转矩控制的整体框图如图6所示，主要由三部分组成，分别是新型双坐标观测器、基于双坐标系的电磁转矩及定子磁链预测以及评价函数优化。

图6 整体控制系统流程图Fig.6 Block diagram of the overall control system

3 实验结果

3.1 实验平台

所提出的算法在感应电机实验平台上进行验证。实验平台由一台2.2 kW的感应电机与永磁同步电机联结组成。感应电机作为预测算法实施控制的驱动电机，其中数字处理器采用TMS320F28335，电机参数为：VDC＝540 V，Rs＝2.68 Ω，Rr＝2.13 Ω，Lm＝275.1 mH，Ls＝Lr＝283.4 mH，pn＝1.0，J＝0.005 kg/m2；永磁同步电机作为负载电机，主要目的是为感应电机提供负载转矩，由通用变频器控制。在本实验中，感应电机的状态变量通过数模转换器后由示波器显示。转子位置通过永磁同步电机自带的增量式编码器获得。

3.2 实验结果

3.2.1 整体性能

感应电机的正、反转实验结果如图7所示。图中，感应电机的转速指令设置为从2 772 r/min到-2 772 r/min，而后返回至2 772 r/min。定子磁链幅值的指令设置为0.71 Wb。

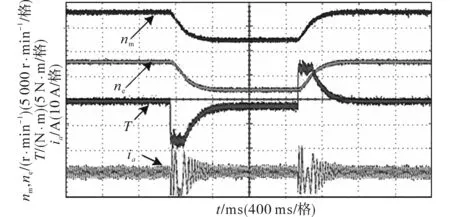
图7 感应电机正、反转实验Fig.7 Forward and reverse rotation experiment of IM

在图7中，从上至下，依次为测量感应电机转速、估计转速、电磁转矩和定子电流波形。从图中可看出，感应电机正、反转整体性能良好。在转速动态调节过程中，电磁转矩最大值为7.5 N·m，此值为转速环输出的限幅值，同时也是感应电机的额定转矩。

在感应电机的正、反转过程中，测量转速与估计转速的误差如图8所示，其中，两者误差的计算公式为

从图8中可看出，在感应电机低速区，转速估计误差较大，特别在正、反转过渡的零速附近，转速误差可达4%。

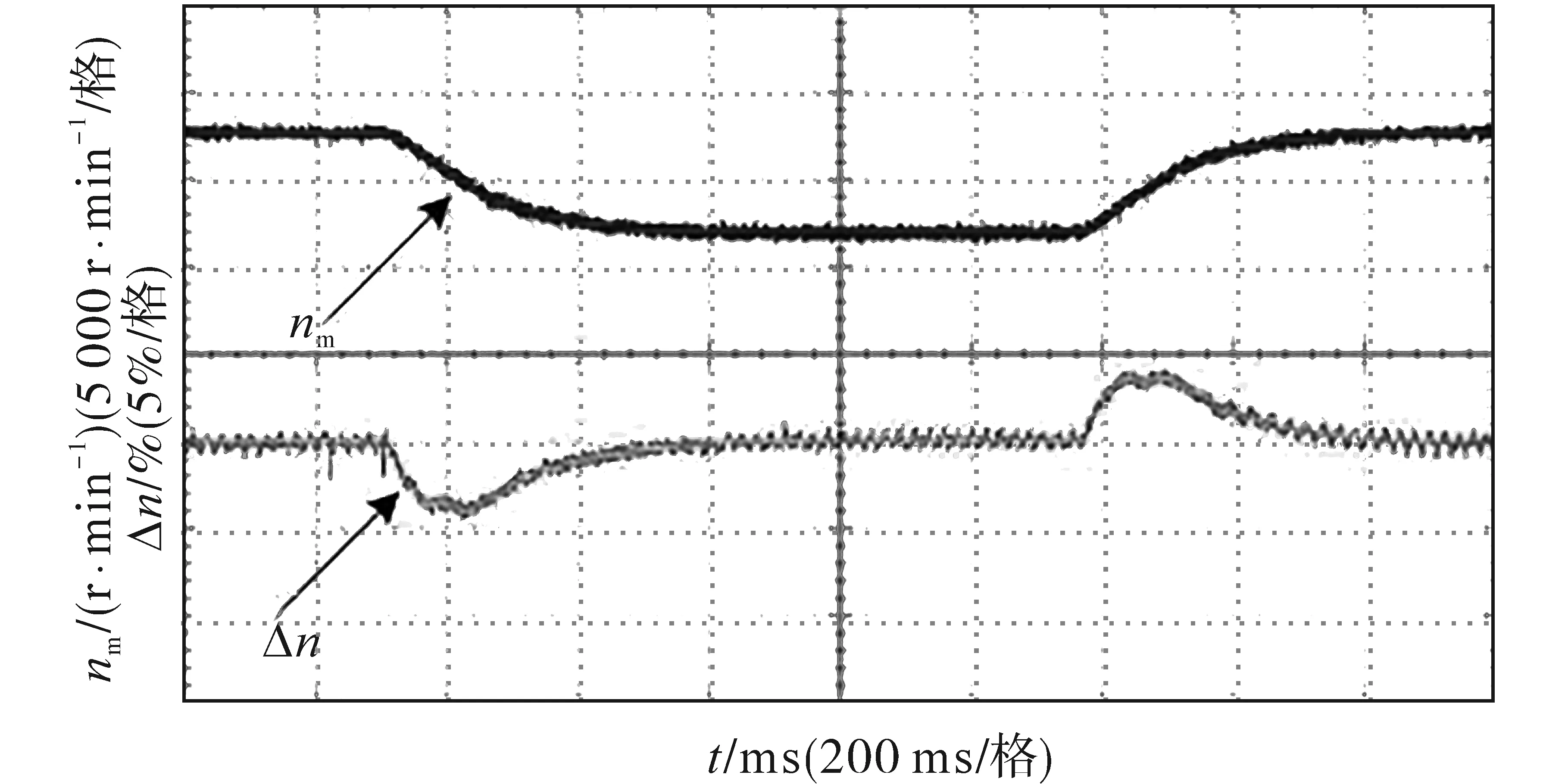
图8 正、反转转速估计误差Fig.8 Forward and reverse speed estimation error

3.2.2 稳态性能

在转速指令为1 385 r/min，定子磁链幅值指令为0.71 Wb以及负载转矩为5 N·m条件下（此负载转矩由永磁同步电机提供），感应电机的稳态性能如图9所示。从图9可知，定子磁链幅值基本保持在0.71 Wb；电磁转矩波动较低，波动范围小于1.5 N·m；定子电流波形较好，总谐波扰动（total harmonic distortion，THD）为4.5%。

图9 感应电机稳态实验Fig.9 Steady state of induction motor

3.2.3 低速区转速观测

在低速轻载状态下，由于感应电机定子电流以及反电动势过小，因此转速观测器的性能会变差。为了验证提出的观测器在低速区的性能，感应电机的转速指令设置为60 r/min，然后突变至30 r/min，此时电机处于空载状态。感应电机测量转速、估计转速、定子磁链幅值以及定子电流波形如图10所示。从图10可以看出，即使在低速空载状态下，所提出的转速观测器仍具有良好的性能。

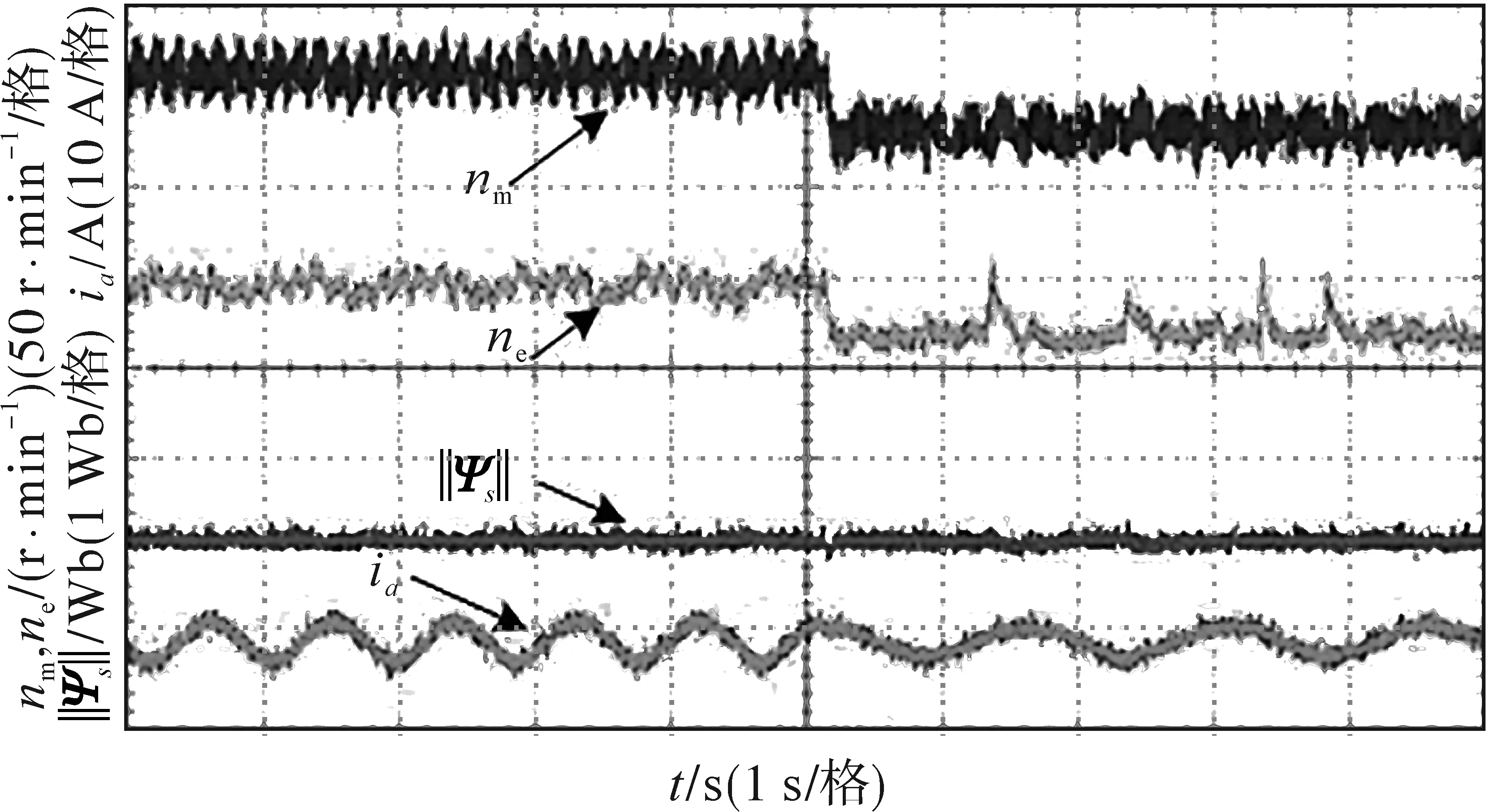
图10 低速区转速估计Fig.10 Speed estimation at low speed areas

3.2.4 负载扰动响应

当感应电机转速指令为1 500 r/min且实际转速稳定时，通过通用变频器控制负载电机，使负载转矩从0 N·m突加至7.5 N·m，感应电机的动态响应如图11所示。从图11可以看出，预测转矩控制具有快速的电磁转矩动态响应，由于突加负载转矩引起的转速降低，在较短的时间内得到了快速恢复。

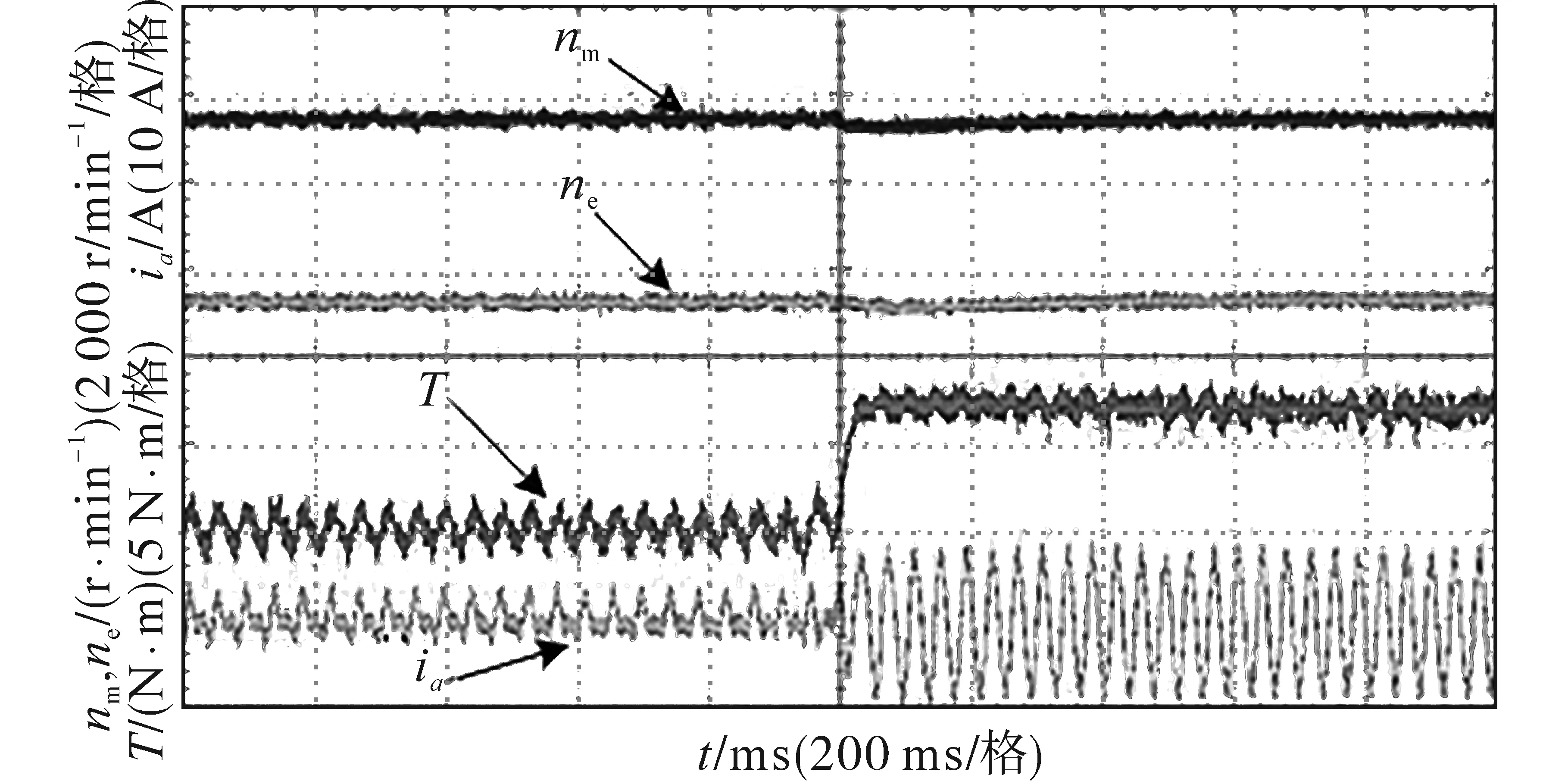
图11 负载扰动响应Fig.11 Load disturbance response

4 结论

针对无速度传感器感应电机预测转矩控制存在的问题，提出了新型双坐标系观测器、双坐标系电磁转矩预测模型。主要结论如下：

1）提出的新型双坐标系观测器分离了定子磁链观测和转速估计，实验结果表明，此观测器在感应电机正反转、高速以及低速下均具有良好的性能。

2）提出的双坐标系转矩预测模型不需要转速信息，进一步提高了电磁转矩的预测精度，实验结果表明，此算法在电磁转矩阶跃指令以及负载转矩阶跃突变情况下，均具有快速的动态响应。

3）实验结果验证了双坐标系预测转矩控制的有效性，具有较好的动态性能和稳态性能。因此，该方法可应用于实际的电机驱动系统中。

需要注意的是，感应电机的整体控制性能不仅与转速磁链观测器、转矩预测模型有关，同时也与速度控制器有关；此外预测转矩控制属于开环高增益控制范畴，高动态响应的同时也具有弱鲁棒性的特点。进一步提高预测转矩控制的动态性能以及鲁棒性能成为下一步需要深入研究的问题。