基于改进爬山搜索法的风力发电机传动系统控制策略研究
2021-10-11杨德州张中丹皮霞孙晓光耿建宇韩袁
杨德州,张中丹,皮霞,孙晓光,耿建宇,韩袁
(1.国网甘肃省电力有限公司电力经济技术研究院,甘肃兰州730000;2.国网吉林省电力有限公司长春供电公司,吉林长春 130021)
近年来,随着化石能源的持续高消耗,由于化石能源是不可再生能源,因此能源的可持续性成为了一个重要问题[1]。此外,在使用化石能源时,将会带来环境恶化问题,包括温室效应以及全球环境污染等[2]。发展清洁能源逐渐替代传统化石能源成为世界各国可持续化发展的必然趋势。水能、风能以及太阳能等可再生能源受到越来越多的关注,将在今后能源消耗中所占比重越来越大[3]。其中,风能是一种分布广、储量大的可持续能源,并具有对生态影响小、不会产生污染以及方便利用等优势,因此风能受到了广泛的关注[4-5]。
在风力发电系统中,由于风速具有瞬变性,造成风力发电系统的输出功率不稳定,且受外界环境干扰严重[6-7],从而风力发电系统的输出功率将无法达到预期的输出功率。为了能够有效地增加在不同风速情况下系统的输出功率,需要对风机的转速进行合理地调整,使其与风速相匹配,最终达到最大风能捕获,并能够进一步增加发电系统的输出功率。因此,针对一种能够有效控制风机转速和实现最大功率跟踪方法的研究亟待解决。
如今,被广泛应用在风电系统最大风能捕获的主要方法有:叶尖速比控制法、功率反馈法、爬山搜索法等[8-11]。叶尖速比控制法对风速的准确测量有很高的依赖性,因此其对风速传感器以及叶尖速比曲线的精准度要求也比较高,但是在现实环境中通常不能保障该精准度。因此,在新型以及改进控制方法的研究中,一般采用基于实现方法较为简单的爬山搜索法。该方法不需要知道风速,是一种普遍且简单的最大风能捕获的方法。传统的爬山搜索法为了能够获得最大风能捕获方法,其步长需要有效调整,否则将会影响系统的稳定和输出特性。目前针对该特点常用的改进方法有模拟退火法的改进型爬山搜索法、电导法以及模糊推理最优梯度法等[12-16]。上述改进方法将定步长爬山法改进成为变步长搜索,从而实现较为稳定输出以及动静态特性。然而,这些方法目前还存在计算量大、结果出现振荡以及输出功率提升效果不显著等问题。
本文为了优化风力发电系统的控制策略,并提高其发电效率,针对基于模糊控制改进爬山搜索法的风力发电机传动系统控制策略展开了一系列研究。首先,针对风力发电机的风速和风力机进行数学建模,通过分析传统爬山搜索法的控制流程和方法,引入了模糊控制策略对系统中的PI参数进行有效调节,并搭建Simulink仿真模型,获得改进爬山搜索法的仿真结果。最后,将改进方法与传统方法进行对比,从而对该方法的可行性进行验证,其结果具有一定的工程实际意义。
1 风力发电机的风速和风力建模
1.1 风速系统模型
风力发电机所涉及的风场主要有基本风、阵风、渐变风以及随机风几种类型,并且具有间歇性与随机性的特点[17]。基本风Vb也被命名为平均风,其数学模型为
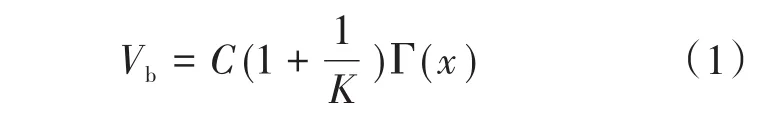
其中
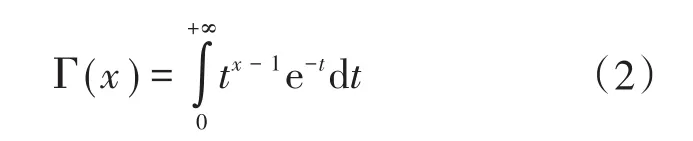
式中:C为威布尔分布的尺度;K为威布尔分布的形状;Γ(x)为伽玛函数,该函数是阶乘的延拓,是定义在复数范围内的亚纯函数。
渐变风Vg表现风速的渐变情况,其数学模型如下式:
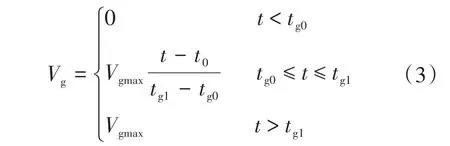
式中:Vgmax为渐变风在该段时间内的风速最大值,m/s;tg0,tg1分别为渐变风的变化开始时间和结束时间。
根据实际对风机遇到的渐变风情况,设定其参数:渐变风的变化开始时间为2 s,变化结束时间为8 s,最大风速为4 m/s。
阵风Vf能够表现风速突然变化的特性,其数学模型为
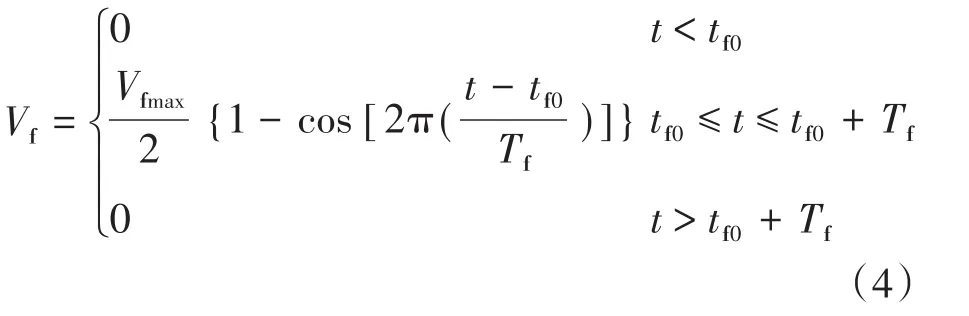
式中:Vfmax为阵风在该段时间内的风速最大值,m/s;tf0为阵风的变化开始时间;Tf为阵风的周期。
根据实际对风机遇到的阵风情况,设定其参数:阵风的变化开始时间为2 s,周期为3 s,其最大风速为3 m/s。
随机风Vr能够表现风速的随机波动情况,其数学模型为
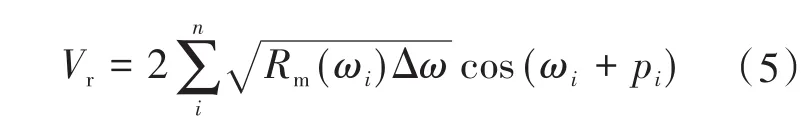
其中

式中:Rm(ωi)为在风速第i个变量的风速最大值;ωi为风速的第i个变量角频率;Δω为风速变量间的离散距离;pi,vf分别为随机变量和相对高度的平均速度;Kr,F分别为地表粗糙度系数以及风速的扰动区间。
根据实际对风机遇到的阵风情况,设定其参数:随机风的随机分量的幅值为1 m/s,波动平均间距范围为0.5π~2π rad/s。
在实际的风场里风速是为组合风的形式,其数学模型表示为

1.2 风力机特性及其系统模型
根据空气动力学原理[18],风力机的输入功率表达式为

式中:ρ为空气密度,标准大气压下其值为1.29 kg/m³;R为风机叶片的半径;v为风速。
风力机的输出功率表达式为
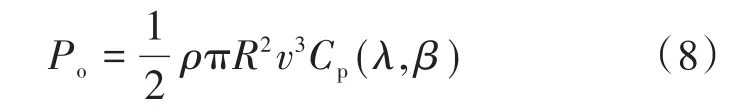
其中

式中:Cp(λ,β)为风力机能够把风能变化为机械能的效率,即风能利用系数;λ,β分别为叶尖速比以及桨叶节距角;ω为风机叶片旋转的角速度,rad/s。
若桨叶节距角β的值保持一致,则风能利用系数Cp与β的值无直接相关关系,该系数Cp仅与叶尖速比λ有关,其两者的关系如图1所示。从图中可以看出,当β的值为0时,其叶尖速比的值为8.1,此时风能利用系数为最大值,达到0.48。所以,在不同风速情况下,有且仅有一个转速与该风速最为匹配,从而能够获得最大捕获功率。在不同风速情况下,将所得到的最大捕获功率值进行连接,则获得风机输出最大功率曲线图,其为一个二次函数。因此,最大功率控制的原理即为在不同风速条件下,通过对风机转速进行调整,从而使其功率能够最为靠近最大功率曲线。
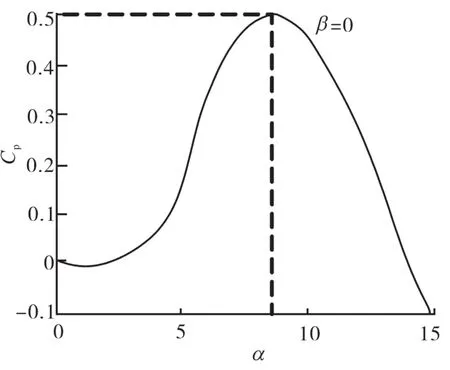
图1 风能利用系数与叶尖速比的关系Fig.1 Relationship between wind energy utilization coefficient and tip speed ratio
因此,采用的变速风力机的Cp(λ,β)表示式定义为
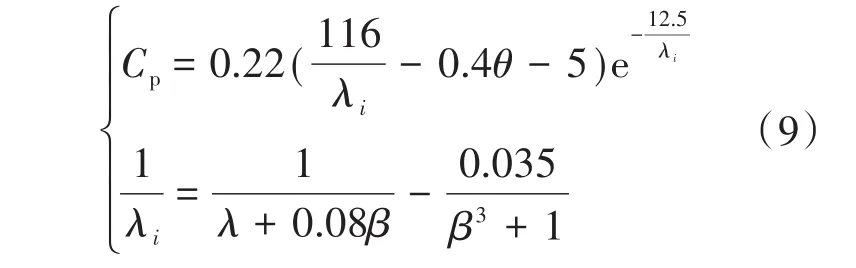
2 改进爬山搜索法模型建立
2.1 改进爬山搜索法
爬山搜索法主要思想为持续调整风力机转速,匹配其功率变化,从而达到最大功率跟踪,对风力机以及风速的相关指标并没有要求[11]。风力机捕获功率P与电机转速ω之间的关系如图2所示。
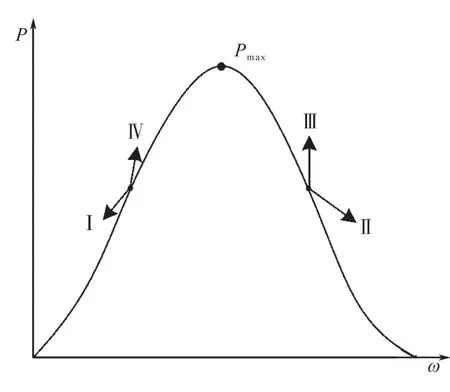
图2 爬山搜索法原理图Fig.2 Schematic of climbing search method
通过对曲线进行求导,得到风力机的最大捕获功率,此时其导数dP/dt的值为0,并对图2的曲线进行区域划分,其结果如表1所示。
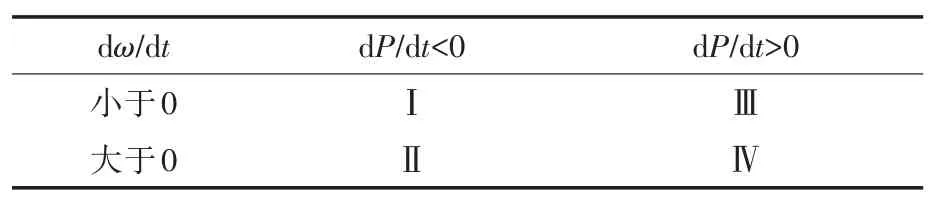
表1 爬山搜索法逻辑表Tab.1 Logic table of climbing search method
爬山搜索法的主要步骤为:1)测量电机的转速ωn以及风力发电系统的捕获功率Pn;2)测量电机转速和风力发电系统的功率的变化量Δωn和ΔPn,其值分别为ωn-ωn-1和Pn-Pn-1;3)依据所得变化量结果获得其落在Ⅰ区、Ⅱ区、Ⅲ区和Ⅳ区中的哪个区域内,并加入一个角速度扰动S,该扰动被定义为S=sign(ΔPn/Δωn)× s× |ΔPn/Δωn|,其中,s为固定常数;4)输出调节后的转速;5)重复以上步骤。具体流程如图3所示。
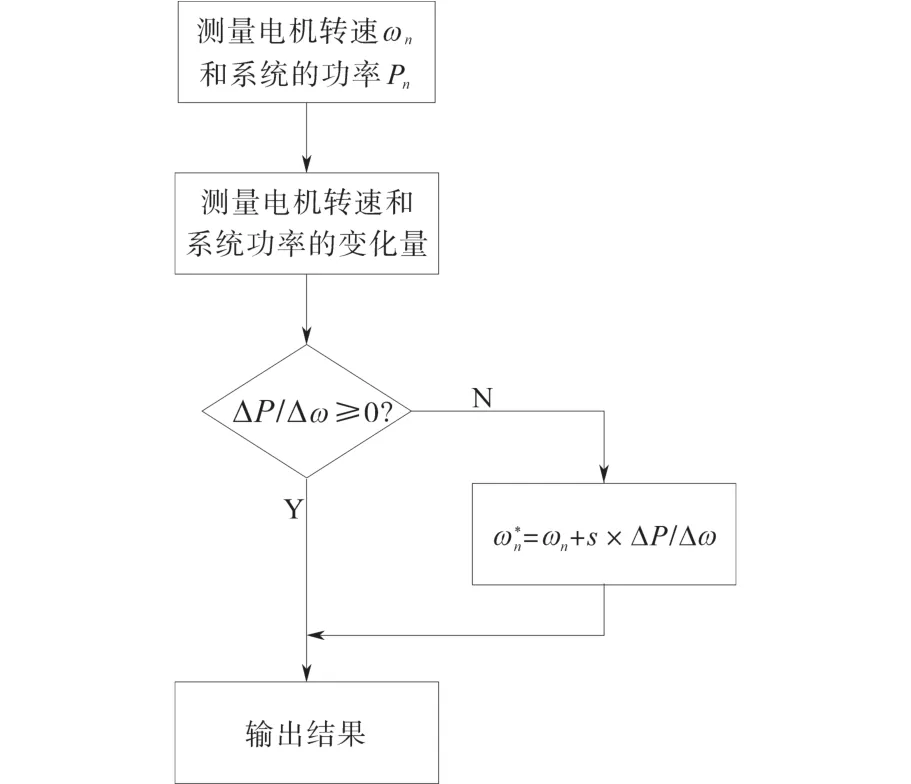
图3 爬山搜索法的具体流程图Fig.3 Specific flow chart of mountain climbing search method
利用爬山搜索法在进行最大功率跟踪优化过程中,以恒定转速进行适应性调整,保证系统运行在最大功率点附近,但考虑风速不稳定性,最大功率点会出现一定波动。此时若扰动步长选择足够小且合理,其波动也将在能允许的范围内。针对固定步长的爬山搜索法,若其步长选择较大,则将造成在最大功率点产生的波动较大;若其选择较小,则将造成初始阶段的跟踪效率不足,无法达到足够快速响应。因此,需要对其如何能够较为合理地选择步长进行进一步研究。
2.2 基于模糊控制策略改进爬山搜索法
由于爬山搜索法受步长影响较大,因此引入模糊自适应控制对传统爬山搜索法进行改进,从而能够合理选择步长,增加计算效率和精度。
风力发电系统传统PI调节器的效果主要依赖风力发电系统的性能,此外,由于其调节器参数无法实时调整,造成系统无法进行最优的控制[19]。随着模糊神经系统的应用越来越普遍,引入该算法能有效地对PI参数进行调整,从而匹配实际条件,使系统达到最佳控制效果[20]。
模糊神经系统的结构和神经网络类似,也是利用模糊隶属度函数的输入与输出的数据集合。简单的模糊推理神经系统结构,即将三个输入参数经过模糊化处理,从而构造模糊集合以及模糊规则,并将获得的数据通过解模糊化,最终获得输出结果。模糊推理系统结构如图4所示。
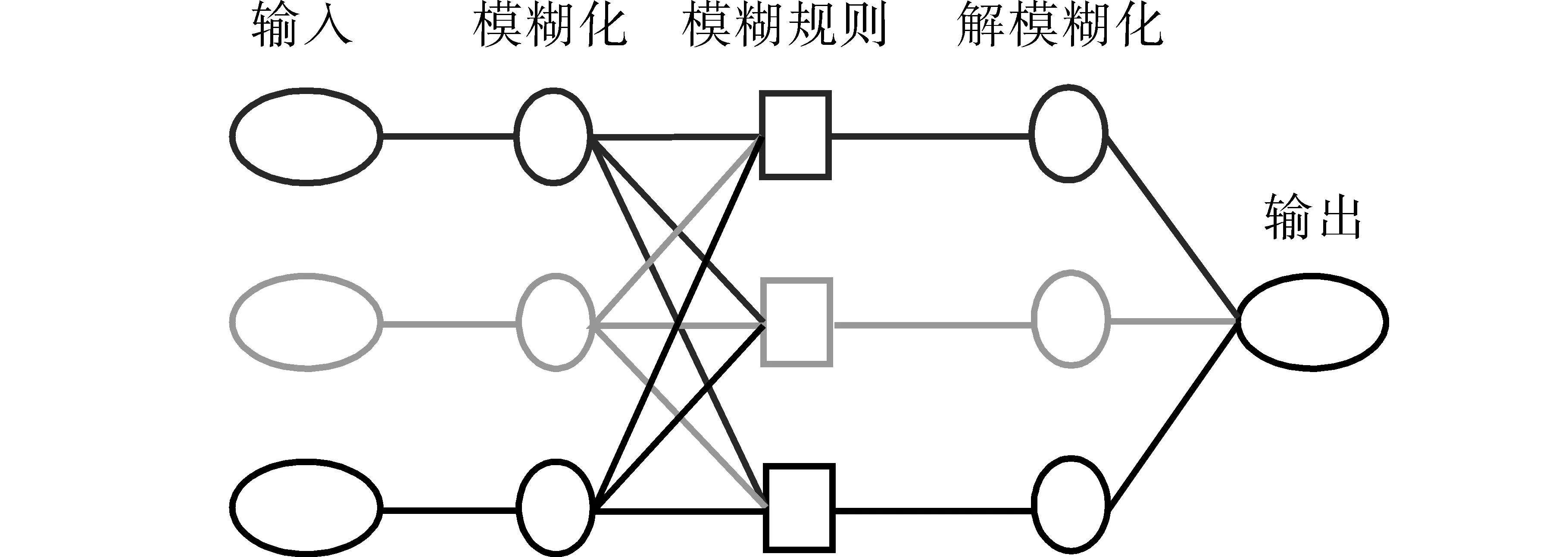
图4 模糊神经系统结构图Fig.4 Structure diagram of fuzzy neural system
模糊PI控制系统结构如图5所示。其中,该系统的核心模块是模糊控制器,该控制器主要由模糊化、数据规则库、模糊推理以及解模糊化等几个部分组成。该控制器通过将误差e以及其微分ec作为输入数据,然后对该数据展开模糊化处理,接着通过模糊推理以及进行解模糊化,从而得到ΔKp和ΔKi。
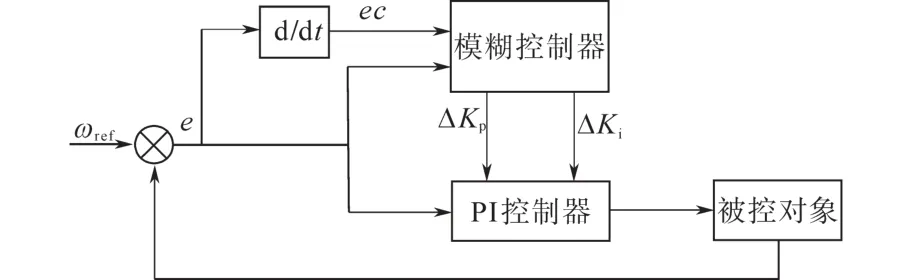
图5 模糊PI控制系统结构示意图Fig.5 Structure diagram of fuzzy PI controller
从输入语言变量中选择模糊集合{正大(PB),正中(PM),正小(PS),零(ZO),负小(NS),负中(NM),负大(NB)}。进而令输入输出的模糊集合分别定义为:误差e,微分ec,ΔKp以及 ΔKi,它们均定义为{负大,负中,负小,零,正小,正中,正大},因此其ΔKp以及ΔKi的模糊规则库如表2和表3所示。
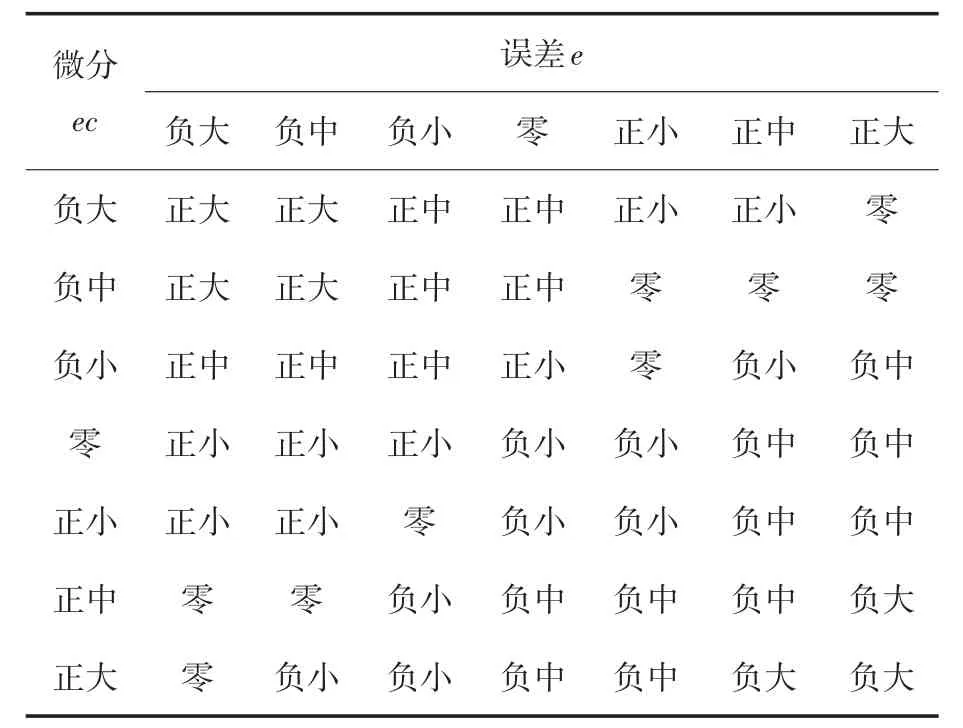
表2 ΔKp的模糊规则表Tab.2 Fuzzy rule table ofΔKp

表3 ΔKi的模糊规则表Tab.3 Fuzzy rule table ofΔKi
基于模糊控制策略改进爬山搜索法搜索不同风速和转速,其步骤如下:1)基于在不同风速条件下电机转速和风能利用系数之间的关系,以及不同风速条件下的步长关系进行神经网络训练,从而得到模糊推理的隶属函数与模糊规则;2)测量风速vn,永磁同步电机的转速ωn和风力发电系统的功率 Pn;3)计算风能利用系数 Con;4)利用前面所得模糊规则对步长进行有效调整;5)输出步长调节后的转速;6)重复前述步骤。
3 仿真系统搭建
针对基于模糊控制策略改进爬山搜索法进行仿真研究,在Simulink中搭建仿真模型。
3.1 风速系统仿真模型
现实中的风场为组合风的形式,是由第1节中的基本风Vb、阵风Vf、渐变风Vg以及随机风Vr组成的,根据组合风的数学模型(即式(6))搭建Simulink模型,该模型输出由4种不同形式风组成,其模型与仿真的波形图如图6所示。其中图6a为仿真模型,图6b为其仿真输出波形。从中可以看出,组合风在前期变化较大,在8 s后逐渐趋于稳定。
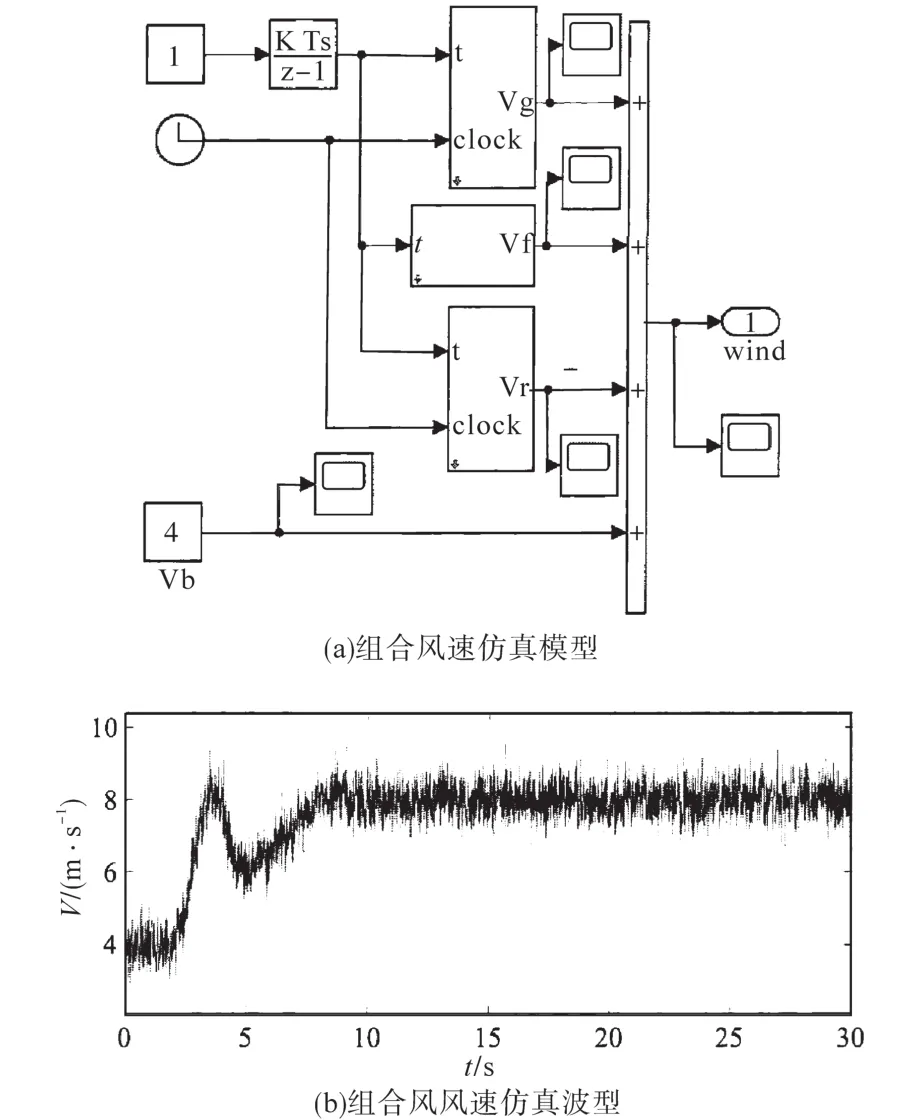
图6 组合风仿真模型及其波形Fig.6 Simulation model and waveform of combined wind
3.2 风力机系统仿真模型
在不同风速条件下,风力机系统的最大风能利用系数不一样,并且最大风能利用系数所最佳匹配转速也不一致。而且,随着风速的变大,最佳匹配转速也随之上升。在不同风速条件下,风力机系统的最佳输出功率也不一样。因此,在对风力机系统进行仿真时,需要将风速和风机转速作为输入量,并根据式(8)、式(9)搭建相关Simu⁃link模型,其模型如图7所示。其中,风力机的参数设置如下:叶片半径32 m,空气密度1.2 kg/m3,额定功率1.5 MW,最佳叶尖速比8,最大风能利用系数0.48,惯性常数4.32。当风力发电机在进行最大风能捕捉时,通过调节转速将功率点进行调节,从而达到最佳输出功率。

图7 风力机系统仿真模型Fig.7 Wind turbine system simulation model
3.3 爬山搜索法系统仿真模型
爬山搜索法利用功率以及电机转速的变化情况进行期望转速的搜索,并通过PI控制得到电机转矩。爬山搜索法的主要流程是先获得电机转速和风力发电系统的捕获功率,并根据转速和功率的变化量进行角速度扰动,进而调节电机转速,以达到输出最佳匹配转速的目标,其搭建Simulink仿真模型如图8所示。
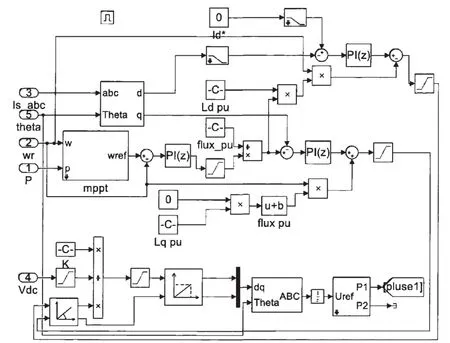
图8 爬山搜索法控制仿真模型Fig.8 Simulation model of climbing search method
3.4 改进爬山搜索法仿真模型
改进爬山搜索法的主要特点是通过模糊策略对步长进行智能调整,该改进方法的主要流程如图9所示,具体为:根据电机转速和风能利用系数之间的关系进行神经网络训练,生成模糊规则,通过输入风速、电机转速以及风力发电功率进行计算,并对结果基于神经网络训练生成的模糊规则进行步长调整,进而调节电机转速并重新计算,直至输出最佳匹配电机转速和风力系统输出功率。

图9 爬山搜索法计算流程图Fig.9 Calculation flow chart of mountain climbing search method
模糊控制器的仿真模型如图10所示,该模块通过模糊算法对传统爬山搜索法的步长进行调整。并将搭建好的模糊PI控制器的Simulink模型代入爬山搜索法中的步长控制,从而通过该模块获得最佳匹配速度的步长,实现提升系统的输出功率。

图10 模糊PI控制器仿真模型Fig.10 Simulation model of fuzzy PI controller
4 仿真结果与分析
基于模糊控制策略改进爬山搜索法在对组合风的仿真中,为了更为直观且有效地进行对比分析,对计算的有功功率P和无功功率Q进行标幺化,其结果如图11所示,对系统的电压以及电流影响情况如图12所示。
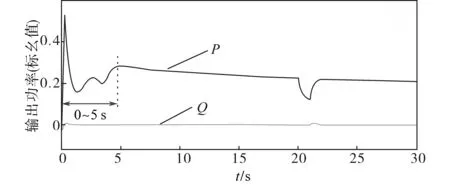
图11 有功功率P和无功功率Q计算结果Fig.11 Calculation results of active power P and reactive power Q
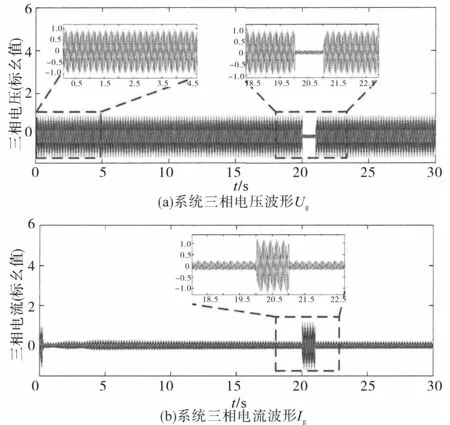
图12 系统电压、电流波形Fig.12 Voltage and current waveforms of system
通过对结果进行分析,能够得到:基于模糊控制策略改进爬山搜索法在0~5 s阶段仍有较大的波动,但在控制器的作用下,系统在5~30 s的时段内,风力发电的有功输出P逐渐稳定,并且系统的无功输出Q始终保持在0附近浮动,不会因有功输出P的变化而随之改变。因此,该模糊控制器下的风力发电系统对整个电网系统的电能质量影响不大。在20 s处因电网出现短暂故障,系统的电压随之产生下降,电流突然升高,此时风力发电机的有功输出P也随之有所降低,由0.23(标幺值)下降为0.13(标幺值)。为了恢复系统的有功输出,该系统加了无功输出,在21 s处开始上升,由0.000 14(标幺值)增大至0.008 9(标幺值)。有功输出在无功功率介入后,开始迅速恢复。随着有功功率的恢复,无功功率开始逐渐回落,并在22.5 s处恢复到0。此外,系统的电压以及电流在21 s处,无功功率介入后,即刻恢复了电压暂降前的状态,满足系统要在2 s内恢复的规定,也表明了该风力发电机在该控制器的作用下呈现出一定的低电压穿越特性。
定子电压和电子电流的仿真结果如图13所示。从图中可以看出,由于风速的不稳定性,定子的电压在初期0~2.8 s时段内产生一定的振荡,定子电流则在0~1.1 s时段内具有较大的波动。通过控制器的调节作用,定子的电压和电流信号逐渐稳定。在20 s系统电压出现暂降时,定子电压也出现降低,而电流则是较为稳定。在无功功率介入后,定子电压也在21 s处迅速恢复了稳定。因此,风力发电系统在基于模糊控制策略改进爬山搜索法的调节作用下运行状态较平稳。
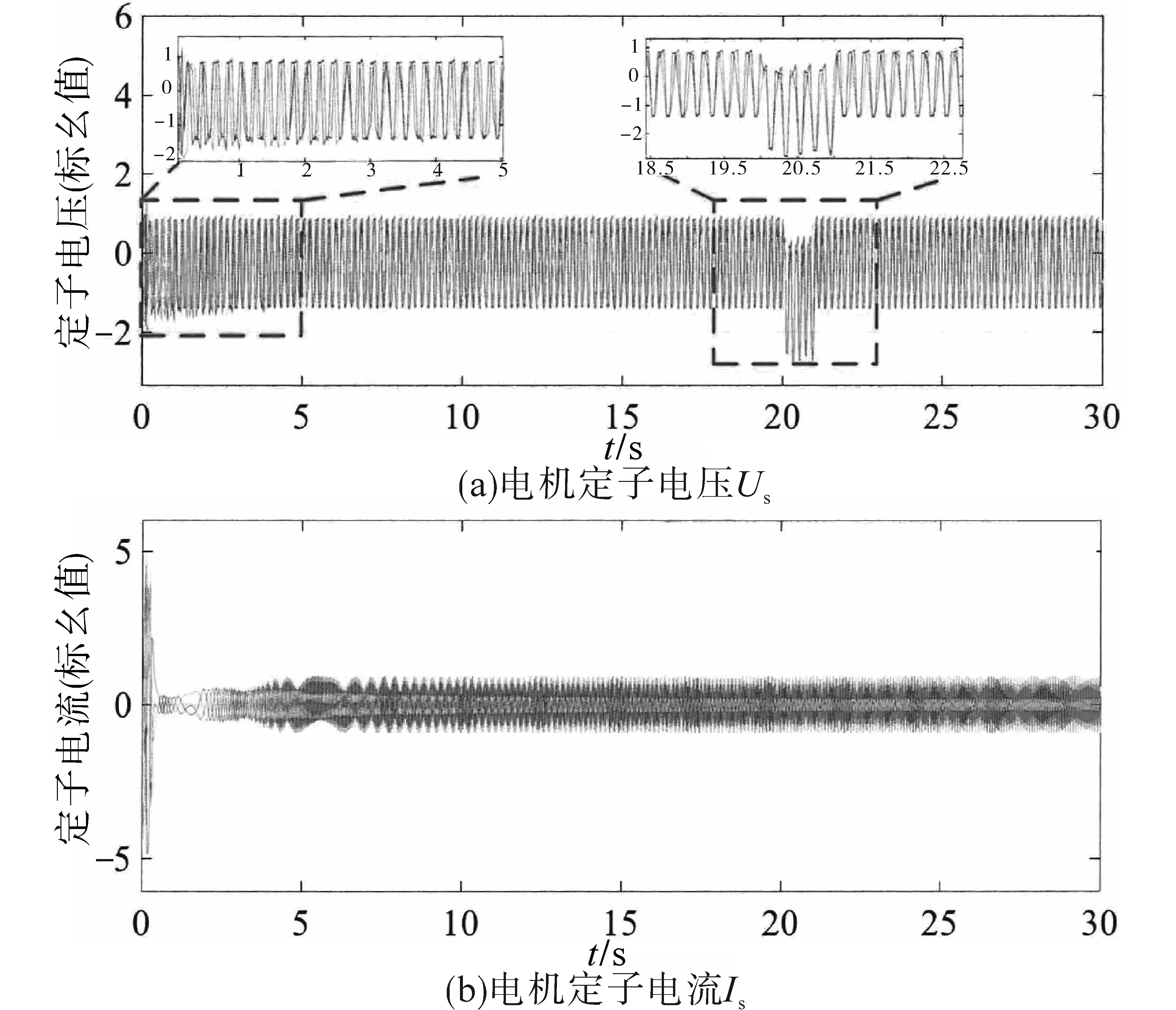
图13 电机电压、电流波形Fig.13 Voltage and current waveforms of motor
将基于模糊控制策略改进爬山搜索法与定步长爬山搜索法、变步长爬山搜索法进行对比,分别在同一风速情况下对系统有功功率和无功功率进行仿真计算,并进行对比分析。针对同一组合风的仿真结果如图14所示。从图中可以看出,使用基于模糊控制策略改进爬山搜索法进行搜索,其效果比传统爬山搜索法有显著的提升。在0~5 s时段内,大大降低了由于风速波动较大所造成的系统输出功率的振荡,较好地弥补了传统爬山搜索法在起始阶段波动较大的不足。此外,在该时段内,系统的功率也有所提高。在5~20 s间,系统输出均较为稳定,在20 s处由于电网故障,系统有功功率出现暂降,为恢复系统稳定,无功功率在21 s处均出现小幅度上升。

图14 不同方法的系统功率对比图Fig.14 System power comparison diagram of different methods
三种方法所得到的电机转速仿真结果如图15所示。从图中能够得到:在0~5 s处,由于风机起始转速大,因此该阶段风速不稳定,从而导致搜索方法产生错误,造成风力发电机转速不能快速达到最佳匹配转速。基于模糊控制策略改进爬山搜索法相对于传统爬山搜索法而言,在该时段内,转速最为靠近最佳匹配转速,且较为稳定。在5~30 s的时段内,风速总体趋势比较平稳,但是还存在高频波动,改进爬山法与定步长爬山法得到的转速相比变步长爬山法而言,要更加平稳,搜索得到的转速更加接近最优转速。

图15 不同方法的电机转速对比图Fig.15 Motor speed of different methods
在0~30 s内三种方法的有功功率平均值如表4所示。从表中可以得到:在0~5 s内,基于模糊控制策略改进爬山搜索法比定步长爬山搜索法功率提高了25.8%,相比与变步长爬山搜索法功率提高了10.2%。在5~30 s内,基于模糊控制策略改进爬山搜索法比定步长爬山搜索法功率提高了3.8%,相比与变步长爬山搜索法功率提高了8%。从整体效果来看,改进爬山搜索法比定步长爬山搜索法功率提高了8.7%,相比与变步长爬山搜索法功率提高了8.3%。

表4 三种方法的有功功率平均值Tab.4 Average value of active power under three methods
5 结论
本文研究了基于模糊控制改进爬山搜索法的风力发电机传动系统控制策略。根据风力发电机进行数学建模,引入模糊控制策略对系统中PI参数进行控制的改进爬山搜索法,并通过Simulink仿真得到:基于模糊控制的改进爬山搜索法能够有效降低在0~5 s内的系统有功功率振荡现象,并当系统发生故障出现电压降时,也能更有效地使系统恢复正常状态。在0~5 s内,改进爬山搜索法比定步长爬山搜索法功率提高了25.8%,相比于变步长爬山搜索法功率提高了10.2%。从整体效果来看,改进爬山搜索法比定步长爬山搜索法功率提高了8.7%,相比于变步长爬山搜索法功率提高了8.3%。从而也对该方法的可行性进行了验证,其结果对风力发电系统的控制具有重要的参考意义,进一步推动电网自动化技术的智能化程度。
