冲击载荷作用下LNG燃料罐防波板参数多目标优化

2021-10-11马寒阳董金善

船舶力学 2021年9期

马寒阳，董金善

（1.南京工业大学机械与动力工程学院，南京 211816；2.华东理工大学机械与动力工程学院，上海 200237）

0 引言

船用LNG燃料罐作为一种移动式低温压力容器，在运行的过程中不仅要承受内外压载荷，还会受到由于惯性力或碰撞引起的液体冲击载荷。冲击载荷引发的液体晃动现象会带来不利的影响：一方面，对燃料罐结构产生冲击载荷；另一方面，液体的大幅晃动将会改变载荷分布，产生附加的力和力矩，从而降低船的行驶稳定性。因此，开展船用LNG储罐内液体晃动的数值方法研究及防波板的设计具有重要的学术价值和工程指导意义。目前，晃荡问题主要从理论、实验和模拟三个方向进行研究。Li[1]研究了直接时域理论和间接时域理论对船舶运动的时延函数的影响，结果表明间接时域理论在处理无航速和较低航速工况下显得更加高效实用；杨志勋[2]采用二维八边形舱晃荡模型进行了实验，利用广义极值分布、三参Weibull分布和两参Weibull分布预测了晃荡荷载峰值；Elahi[3]使用VOF方法研究了直线加速度和角加速度作用下二维燃料罐的晃荡问题，并与理论计算和SPH方法进行了对比，证实了VOF方法的准确性。

防波板的安装能够有效地减少燃料罐封头承受的压力，提高内外罐间径向支撑结构环氧玻璃钢的支撑能力。国内外学者对防波板进行了大量的研究：Kim[4]利用神经网络和遗传算法对矩形容器在平移载荷作用下的防波板进行分析，得到了防波板的最佳安装高度；王鹤鹏[5]研究了防波板的数量、位置和几何形状对晃荡冲击力的影响；Ma[6]采用VOF模型和大涡模型（LES）模拟研究了不同类型垂直防波板对液体瞬态晃动的有效性。结果表明两个垂直挡板的适当分布可以将峰值冲击压力降低三倍左右。不过，国内外对防波板的研究主要集中在防波板对液体冲击力的减少上，很少有学者针对防波板自身的强度进行分析。目前，仅有Shimanovsky[7]和Kang[8]等对防波板的强度进行了分析。且国产防波板易产生裂纹或松脱，据统计约占总数的90%以上[9]。因此，对防波板的防波效果和结构强度两个目标进行优化分析，得到最佳的防波板形状和位置具有重要的意义。

1 理论模型

1.1 控制方程

LNG船用燃料罐中流体部分的控制方程是Navier-Stokes方程和连续性方程。由于湍流过程非常复杂，根据统计学特征规律，采用流动的时均特性信息（例如平均速度、平均压力等）表示方程中任一瞬时的物理量。将Reynold时均方法用于湍流模型中，则Navier-Stokes方程形式为

式中：δij为Kronecker符号；μt为湍动粘性系数，其取决于流体流动状态，而不是流体的物性参数。可建立μt与湍流动能k和湍流动能耗散率ε的关系式

式中，cμ是通过大量数据统计得到的适用于大部分湍流的常数值，一般取0.09。

1.2 VOF模型

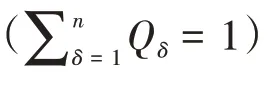
1.3 Fluent环境设置

Fluent采用的有限体积法离散方程适用于结构化网格和非结构化网格。同时动量修正方程和压力修正方程分别使用二阶迎风格式和体积加权法。对于求解压力速度耦合关系，则采用POSI算法[10]。对于冲击载荷，通过UDF（User Defined Function）编写动量源接口程序来施加。因此，计算域中任一有限元网格单元在X、Y上的表达式为[11]

式中：SX和SY分别为计算域中任意有限单元在x和y上的动量源项，单位为N/m3；αx和αy分别为计算域中任意有限单元在x和y上的加速度（本文运动方向加速度取19.62[12]），单位为m/s2；ρ1为气相（空气）的密度（1.225 kg/m3）；ρ2为液相（LNG）的密度（500 kg/m3）；Qx、Qy为计算域中任意有限单元气相、液相的体积分数。

2 防波板有限元计算

2.1 模型介绍

本文以船用低温C型LNG燃料罐内罐为研究对象，筒体内径为1 400 mm，两端为标准椭圆形封头，筒体长度为3 100 mm，有效容积为5 m3。罐内设置锥形防波板，防波板结构参数如图1所示。因模型对称，为提高计算效率，取1/2模型进行分析。防波板及筒体选用S30408，材料性能如表1所示。

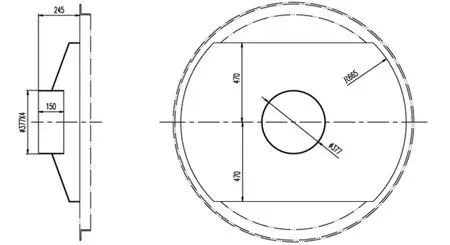
图1 防波板结构参数Fig.1 Baffle structure parameters

表1 材料性能参数Tab.1 Material property parameters

2.2 流体有效性验证

本文借鉴Modaressi-Tehrani[13]论文中使用的模型和参数，用来验证流体算法的准确性。Modaressi-Tehrani采用QS方法计算瞬态液体在纵向加速度为0.3g时对罐体壁面的冲击力。本文通过Fluent有限差分法迭代计算充液率为0.4和0.6两种情况下在一个振荡周期内的平均值。对比情况如图2所示。

图2 Fluent计算值和QS计算值对比Fig.2 Calculated value comparison of Fluent and quasi-static

可以看出，数值计算结果和理论计算结果吻合良好。但是，QS方法只能计算平均冲击力的大小，而不能得到震荡过程中的最大冲击力。本文将采用最大冲击力来计算晃荡对防波板产生的影响。

2.3 不同充液率对罐体冲击力的影响

充装率是影响罐体壁面受力的主要因素之一，但燃料罐罐内液体充装率会经历一个从高到低变化的过程。因此，应该以产生最大冲击力时的充装率作为研究对象。根据文献[14-15]可知，在充装率较小时不会产生最大冲击力，因此，本文取0.5、0.55、0.6、0.65、0.7、0.75、0.8、0.85和0.9九种工况进行研究，如图3所示。

图3 冲击力与充液率的关系Fig.3 Correlation between impact force and filling ratio

从图中可知，液体晃动产生的冲击力先随着充装率增大而增大，充装率大于0.85后，晃动产生的冲击力随充装率的增加而减小，这与文献[14]中研究得到的结果相同。发生这种现象的原因主要是因为当充装率较大时，液体的质量也比较大，因此，液体的晃动幅度就会比较小，所产生的冲击力相应减小。

2.4 数值模拟结果与分析

根据JB4732《钢制压力容器—分析设计标准》[16]和《天然气燃料动力船舶规范》[12]，对于防波板的应力评定是基于第三强度理论，并对其进行线性化处理。线性化处理是选择危险截面并把各应力分量沿一条应力处理线进行应力计算和分类。根据计算结果，得到的最大应力点位于防波板与筒体上角钢连接处，从最大应力点沿网格厚度方向对应力进行线性化。为保证线性化结果的可靠性，在防波板厚度方向至少有三层以上网格密度。应力云图如图4所示。

图4 LNG燃料罐应力云图Fig.4 Stress contour of LNG fuel tank

根据线性化结果，薄膜应力为155.02 MPa≤1.5Sm，弯曲应力强度为236.24 MPa≤3Sm。由此可知，C型LNG燃料罐防波板满足强度要求，并以此为目标进行优化。

3 防波板优化设计

3.1 正交试验设计

防波板的结构复杂且可变参数较多。参考之前学者进行的大量研究，选取防波板距封头安装距离、防波板底边距中心线距离、防波板顶边距中心线距离和防波板形状四个参数进行研究，每个参数在限定条件内取4个水平。利用有限元软件的流固耦合分别获取封头处的最大冲击力（y1）、防波板薄膜应力（y2）和防波板弯曲应力（y3）计算结果。如果把每一种工况都进行计算则需要进行256次计算。为了节省计算成本，采用正交设计法设计试验。设计正交表时留有一个空列，以便进行残差分析。因此本文采用L16（45）正交表。

列出本文采用的试验方案和仿真结果，如表2所示。其中，A代表防波板距封头安装距离，B代表防波板底边距中心线距离，主要是为了使防波板上部弓形面积小于罐体横断面积的20%；C代表防波板顶边距中心线距离，主要是使防波板的有效面积大于罐体横断面积的40%；D代表防波板形状为平板形、锥形、椭圆形和波纹板形，平板型防波板即为厚度为5 mm的平板；锥形防波板的半顶角α=70°；椭圆形防波板是由长短轴之比为四比一的椭圆构成的；波纹板形防波板的中间区域是由振幅为25 mm，周期为400 mm的正弦函数构成，并随着距离筒体越近振幅逐渐减少直至变成平板，为方便之后进行参数化研究，令它们的形状系数[17]值为1、2、3、4。

表2 试验方案和仿真结果Tab.2 Experimental schemes and simulation results

3.2 方差分析

方差分析可以了解各因素对模拟结果的影响，还可以把由试验条件引起的数据波动和由试验误差引起的数据波动区分开来。对于Ln(mk)正交表，把实验数据按表3填写。

表3 正交表Tab.3 Orthogonal table

方差分析的关键是偏差平方和的分解。

总偏差平方和与总自由度为

各列偏差平方和与自由度为

若将因素A安排在正交表的第j列(j=1,2,...,k)上，则有SSA=SSj，这里的r=n/m。

误差平方和与自由度为

于是得方差分析表4。

表4 方差分析Tab.4 Analysis of variance

表5为各因素对封头冲击力和防波板应力值的方差分析结果。

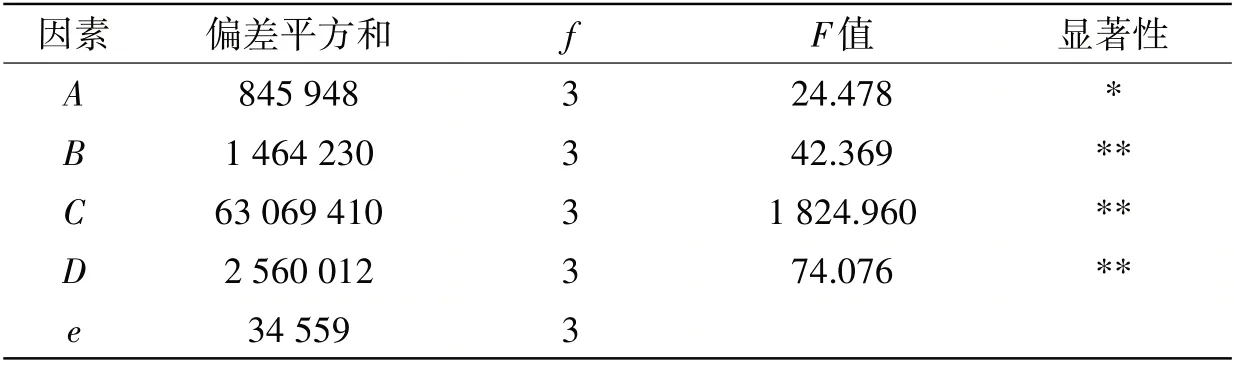
表5 y1方差分析Tab.5 Analysis of y1 variance

表5中，偏差平方和表示因素对试验结果产生的影响，e表示试验误差，利用因素偏差平方和相对于误差平方和来衡量因素的效应，当因素偏差平方和较小时，则可以认为该因素可以忽略不计[18]。取检验水平α为0.05和0.01，查F分布临界值表可知，F0.05(3,3)=9.28，F0.01(3,3)=29.46。当F大于F0.01(3,3)=29.46时，称为因素高度显著，记为**；当F大于F0.05(3,3)=9.28时，称为因素显著，记为*；当F小于F0.05(3,3)=9.28时，称为因素不显著。

综上所述，A、B、C和D四个因素对封头冲击力有显著性影响，其中B、C、D三个为高度显著。根据表6和表7的分析，防波板薄膜应力和弯曲应力产生显著性影响的是A、B和D。选择显著性影响因素作为筛选因子评判标准可以有效地减少工作量，为后续的多目标优化缩小范围。

然而站上演讲台，一切都不一样了。3个多小时的论坛上，David侃侃而谈，详述新西兰葡萄酒的趋势与变化；两个半小时的大师班，David悉心讲解新西兰每个产区、每款葡萄酒的特色与亮点，大师班的开始高呼三声毛利语，激起了整个课堂的气氛；1个多小时站在品鉴会的入口背景板处与葡萄酒爱好者合照、交流，聚光灯的照射下汗水一次次浸湿手帕；4个小时的晚宴上，致开幕词不忘感谢活动的每一位组织者……晚上11点，第十届金樽奖颁奖典礼落下帷幕，David穿过走廊，慢慢地走回房间。留给他与广州相处的时间不多，第二天的中午他又要登上18个小时的飞机，回到新西兰，开始新一周的工作。

表6 y2方差分析Tab.6 Analysis of y2 variance

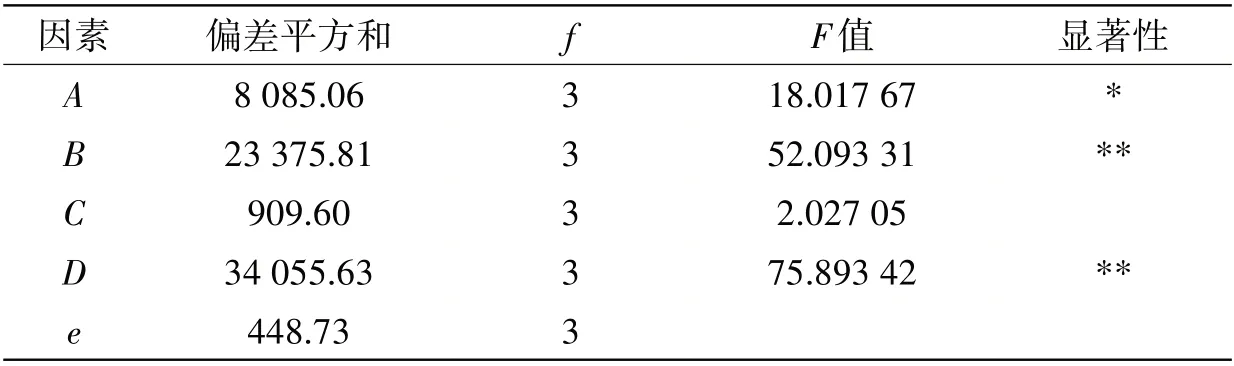
表7 y3方差分析Tab.7 Analysis of y3 variance

3.3 构建回归方程

为了使回归方程可以精确高效地预测非试验点的响应值，回归方程的基本形式采用:

式中：n为设计变量数目；ai、aj和aij为多项式系数。

构造封头冲击力（y1）、防波板薄膜应力（y2）和防波板弯曲应力（y3）的回归方程表达式如下（保留2位有效数字）：

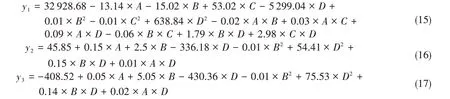
由于回归方程的拟合是一种近似求解，试验数据和响应面回归方程的选择都会给拟合的结果造成影响。因此，选用复相关系数评价回归方程的拟合精度，复相关系数越接近1则说明拟合误差越小。回归方程y1、y2和y3的复相关系数分别为0.990、0.969和0.981。可以看出，回归方程的拟合满足精度要求。

3.4 多目标优化及帕累托（Pareto）最优解

多目标优化问题不存在最优解，而是在相互矛盾的目标函数和限定条件下组成的一系列解的集合，往往一个目标函数的增加是以另一个目标函数的降低为代价，则称这些解为帕累托（Pareto）最优解。因此，在求得帕累托最优解后，要根据工程实际问题从众多最优解中挑选出一个或几个最终解。

本文采用MATLAB优化工具箱中的基于遗传算法的gamultiobj函数进行优化，gamultiobj函数所采用的算法是基于NSGA-Ⅱ改进的一种多目标优化算法。本文以求得的3个回归方程为目标函数，以4个因素的水平上下限为约束条件，求这3个目标函数同时较小时因素的数值。由于防波板线性化结果薄膜应力应小于1.5倍许用应力，弯曲应力应小于3倍许用应力，以此为限定条件，对Pareto解集进行筛选，优选出的Pareto非劣解集如表8所示。

表8 多目标优化Pareto非劣解集Tab.8 Pareto noninferiority solutions

2个Pareto非劣解中，第一组解集具有较小的封头冲击力，相对而言y2和y3的值则偏大。第二组解集的y2和y3较小，但是封头冲击力较大。由于封头采用的是形状系数，需要在平板封头、锥形封头和椭圆形封头三种情况下进行验证，验证结果如表9所示。

表9 多目标优化验证结果Tab.9 Verification results

经过对比考虑选定1号解为最优解，防波效果最好且能够满足强度要求。1号解的封头冲击力为32 328.1 N，相对于未优化之前降低了19.1%。图5为优化后线性化应力沿厚度方向分布图。可以看出，经过优化防波板薄膜应力和弯曲应力均得到降低，优化度分别为12.7%和33.4%。优化得到了良好的效果，对以后工程设计具有借鉴意义。