基于多策略QPSO的半潜式起重平台立柱快速压载舱优化研究
2021-10-11郭蕴华高海波
郭蕴华,董 健,胡 义,高海波
(武汉理工大学a.高性能舰船技术教育部重点实验室;b.能源与动力工程学院,武汉 430063)
0 引 言
半潜式起重平台是一种重要的海洋作业平台,其吊重能力不仅取决于吊机的性能,同时也取决于其快速压载能力。平台在起吊过程中,会产生巨大的倾覆力矩。为了平衡这个力矩,就需要短时间内完成压载水的快速进水和排水。为此,一般会为半潜式起重平台配备快速压载系统,它由空压机、压缩空气管路和快速压载舱室等组成。
对于海洋作业平台的压载系统,已经有学者进行了深入研究。张茴栋等[1]以全回转起重船为对象,通过数值分析法对压载舱进行优化设计,对压载舱各参数指标进行评价,并比较了原方案与优化方案结果。黄超等[2]以大型驳船型起重船为例,对比分析其常规压载、复合压载以及压载舱分层等方案下的压载效果,提出了复合压载及压载舱分层方案。刘志杰等[3]基于船舶静力学和优化理论建立了起重船舶压载水调配优化模型,利用MATLAB优化了具有8个压载舱室的压载水调配过程,以降低起重船舶能耗。潘伟等[4]基于Lingo软件,对全回转起重船作业压载水调节量进行优化,可有效避免经验法可能导致的危险。Samyn等[5]建立了半潜式平台的六自由度动力学压载水控制系统,该系统考虑了压载舱重量、惯性以及力矩的影响。Woods等[6]针对AUV(Autonomous Underwater Vehicle)设计了两套独特的可变压载装置,这两套压载装置分别控制AUV的下水深度以及重心和纵倾横倾角度,可根据工作需要对压载舱进行自动的进排水,实现了压载效率的提高。上述研究都在一定程度上提高了压载效率,但是主要集中于对压载舱室进行分舱分层优化、压载水调节量的优化以及压载系统的智能化操作等方面,没有分析快速压载舱室几何形状对压载效率的影响。
半潜式起重平台立柱快速压载舱优化问题是一类复杂优化问题,具有高维、非线性和复杂约束等特点。对于复杂优化问题,研究人员先后提出了遗传算法(GA,Genetic Algorithm)[7]、粒子群算法(PSO,Particle Swarm Optimization)[8]、差分进化算法(DE,Differential Evolution)[9]、量子粒子群算法(QPSO,Quantum-behaved Particle Swarm Optimization)[10]、生物地理学优化(BBO,Biogeography-Based Optimization)[11]、人工蜂群算法(ABC,Artificial Bee Colony)[12]和布谷鸟搜索算法(Cuckoo search)[13]等智能优化算法进行求解。近年来,孙俊等[14-15]提出了GAQPSO和QPSO_RO等改进QPSO算法,对Benchmark的标准测试算例取得了较好的实验结果。不过,由于实际工程问题的复杂性,有必要对已有算法进行改进以提高优化性能,以求获得更好的优化设计方案。
本文提出半潜式起重平台立柱快速压载舱的多目标优化模型,并提出一种新颖的多策略QPSO(MSQPSO,Multi-Strategy QPSO)算法对其进行求解。计算结果表明,所提的多目标优化模型有利于提高半潜式起重平台的压载效率,且提出的MSQPSO算法较之于已有的智能优化算法在优化性能方面具有明显的优势。
1 问题描述
本文所研究的半潜式起重平台的总体示意图如图1所示。该平台主要由上船体、四根立柱、两个浮箱组成。浮箱分为主浮箱和辅浮箱,且大小不一样,两台最大起吊量为2 200 t的主吊机分别分布在上船体右舷艏艉两处,能够顺/逆时针旋转270°,艏艉带线型,浮箱与立柱、立柱与上船体圆滑过渡。起吊实施的过程中平台装载状态变化较大,为保持平台作业的安全性,平台必须具备快速压载的功能,来保证其稳性平衡。根据总体设计,在起重和卸载工况时,仅通过对立柱快速压载舱(CSBT,Column Side Ballast Tank)重力自流进水和压缩空气排水实现快速压载和排载,而不使用其它压载舱。立柱快速压载舱分布在4根立柱内,为环状结构,分别命名为MP1、MP2、OP1和OP2,其俯视布置图如图2所示。

图1 半潜式起重平台总体示意图Fig.1 Overall diagram of the semi-submersible crane vessel

图2 立柱快速压载舱布置图Fig.2 Layout of the column side ballast tanks
1.1 排水进水时间模型
1.1.1 压缩空气排水
压缩空气排水过程可以分为两个阶段,第1阶段是建压阶段,此阶段海底阀关闭,舱室只充入高压气体而不排水,且充气前舱室内气体压力即为大气压力;等到舱室内压强到达某一阈值时进入第2阶段,此阶段海底阀打开,在高压气体作用下从舱室排水。对于第1阶段,由理想气体状态方程[16]可知:

式中,Qd为空压机排气的体积流量,Pd为空压机排气压力,tc为第1阶段的建压持续时间,P1为建压后舱室内气体压力,Pair为大气压力,V0为排水前的某压载舱室水量体积,Vt为舱室体积。并且,P1和Pair应满足:

式中,h0为舱室初始液位高度,hout为海平面距舱底距离,ρ为海水密度,g为重力加速度。
对于第2阶段,t2时刻的压载舱内的气体压力Pb(t2)和压载水体积Vb(t2)可由式(3)和式(4)计算,

式中,s为海底阀的面积,t时刻快速压载舱海底阀的出水流速v(t)可由伯努利方程推出,

式中,ΔP(t)为t时刻舱室内外压力差,hb(t)为t时刻压载舱内水位高度,k为总阻力系数。
在第2阶段结束时,排水体积Vd与第2阶段的持续时间tf满足如下关系式:

所以,压缩空气排水的总持续时间td为

1.1.2 重力自流进水
重力自流进水过程只有一个阶段,即打开海底阀,水在重力的作用下流入舱室。
在某一时刻t1,压载舱内的压载水体积Vb(t1)可由式(8)计算,

式中,t时刻快速压载舱海底阀的进水流速v(t)也可由伯努利方程推出,
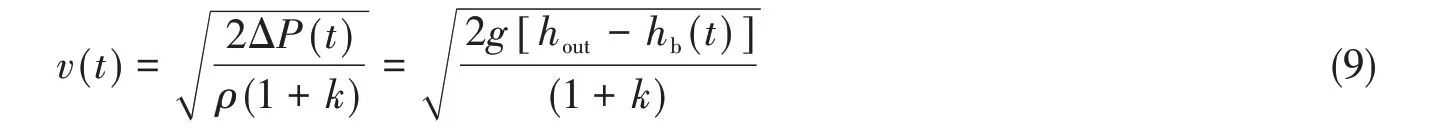
在重力自流进水结束时,进水体积Vg与重力自流进水的持续时间tg满足如下关系式:

1.2 倾角和初稳性高度
平台在起重过程中的总重量W和排水体积V由式(11)和式(12)计算:
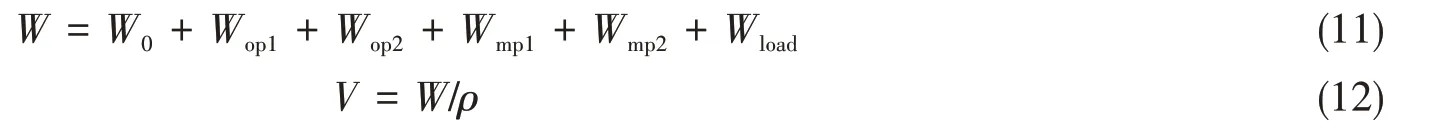
式中,W0是平台除四个立柱快速压载舱室和吊物重量外其它重量总和,Wop1、Wop2、Wmp1和Wmp2分别是4个立柱压载舱内压载水的重量,Wload是吊物重量,ρ是海水密度。
平台在起重过程中的自由液面产生的横向力矩fsmt和纵向力矩fsml由式(13)和式(14)计算,

式中,fsmtop1、fsmtop2、fsmtmp1和fsmtmp2分别是四个立柱舱自由液面产生的横向力矩,fsmlop1、fsmlop2、fsmlmp1和fsmlmp2分别是四个立柱舱自由液面产生的纵向力矩,fsmt0和fsml0分别是起重船除四个立柱舱外其它舱室的自由液面产生的总横向力矩和总纵向力矩。
平台在起重过程中重心的纵向坐标lcg、横向坐标tcg和垂向坐标vcg由式(15)~(17)计算,

式中,Wi、lcgi、tcgi和vcgi是平台各组成部分的重量以及重心的纵向坐标、横向坐标、垂向坐标。平台在起重过程中由自由液面产生的横向力矩修正后的重心垂向坐标vcgfsmt和由自由液面产生的纵向力矩修正后的重心垂向坐标vcgfsml由式(18)和式(19)计算,

平台在起重过程中的初稳性高gmt和纵稳性高gml由式(20)和式(21)计算,

式中,kml和kmt分别是平台的纵稳心垂向坐标和横稳心垂向坐标,可以由排水体积在静水力曲线图表中插值算出。平台在起重过程中的横倾角θheel和纵倾角θtrim由式(22)和式(23)计算,

式中,lcb和tcb分别是起重船浮心的纵向坐标和横向坐标,可以由排水体积在静水力曲线图表中插值算出。起重船在起重过程中的许用重心高度余量avcgm由式(24)计算,

式中,avcg是许用重心高度,可由排水体积在许用重心高度表插值得出,vcg由式(17)定义。
1.3 舱室几何模型
由伯努利方程可知,舱室排水的速度与舱室内的液位高度有关,如果在排水过程中舱室内的液位在一个相对较高的位置,那么排水的速度会适当加快,排水的时间会适当减少。同理,在进水过程中较高的液位会减慢进水速度,增加进水时间。但是,根据建造方提供的原始设计资料,主要典型工况的压载时间主要取决于排水时间。如果优化了排水时间,则总的压载时间将会减少。
因此,将立柱快速压载舱室设计为“上大下小”的形状,使舱室的大部分水量有较高的液位高度,可以在排水量相当的情况下缩减压缩空气排水时间,各立柱快速压载舱主视图如图3所示。
图3中,舱室内环两侧都由两个直面和一个45°斜面相接而成。其中,l1和l2分别为舱室上半部分和下半部分的内环直径,hc为内环直径发生改变的位置。这几个参数是优化设计变量的组成部分。
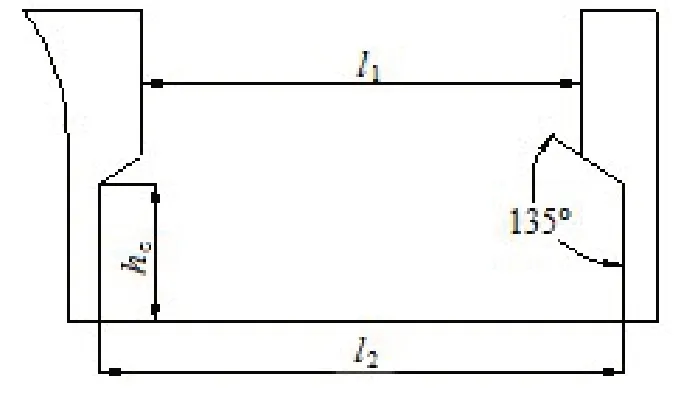
图3 立柱快速压载舱主视图Fig.3 Main view of the column side ballast tank
2 多目标优化模型
本文所研究的半潜起重平台的典型起重工况有8个,分别为:船尾起吊1 400 t、船尾起吊2 200 t、船首起吊1 400 t、船首起吊2 200 t、联合起吊800 t/33°(起重机吊臂的仰角为33°)、联合起吊800 t/22°(起重机吊臂的仰角为22°)、联合起吊2 800 t和联合起吊4 200 t。考虑压载时间和压载水调节量都对快速压载系统的效率有影响,且压载水调节量与能耗直接相关,因此以满足横倾角、纵倾角、稳性高、许用重心高度余量和舱室体积等多个约束条件下最小化8个工况的总压载时间ttotal以及总压载水调节量wtotal为目标函数,这是一个具有复杂约束的多目标优化问题。对于多目标优化问题,工程上经常通过线性加权和法将多目标问题转化为单目标问题来进行求解。对于本文的研究问题,目标函数及其约束条件定义为
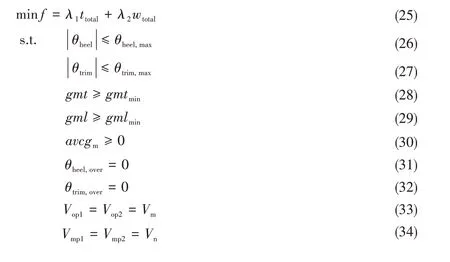
式(25)中,λ1和λ2为权系数,ttotal和wtotal分别由式(35)和式(36)计算。

式中,m=8,ti和wi分别为第i个典型工况的压载时间和压载水调节量,其分别由式(37)和式(38)求得,

式中,ti,op1、ti,op2、ti,mp1和ti,mp2分别为第i个典型工况4个立柱压载舱的进水或排水时间,式(37)表明某一工况的压载时间取这4个时间的最大值;wi,op1、wi,op2、wi,mp1和wi,mp2分别为第i个典型工况4个立柱压载舱的进水或排水水量,式(38)表明某一工况的压载水调节量为这4个水量之和。
根据建造方提供的资料,式(26)~(34)中,θheel,max=1.5°和θtrim,max=0.5°分别为平台起吊过程中所允许的最大横倾角和最大纵倾角,gmtmin=3 m和gmlmin=3 m分别为平台起吊过程中所允许的最小初稳性高和最小纵稳性高,θheel,over和θtrim,over分别为平台起吊完成后的横倾角和纵倾角,Vop1、Vop2、Vmp1和Vmp2分别为四个立柱舱室的体积,Vm=1600 m3和Vn=2 250 m3分别为舱室OP1、OP2所需体积和舱室MP1、MP2所需体积。
式(26)~(30)为不等式约束,式(31)~(34)为等式约束。假定不等式约束可以统一写为g(x)≤0,等式约束可以统一写为h(x)=0,原目标函数为f(x),采用罚函数法定义新的目标函数F(x)为

式中,MC是不等式约束的个数,NC是等式约束的个数,K是惩罚函数因子,通常是正值。只要惩罚函数因子取值得当,可以认为F(x)的最小解足够接近f(x)的最小解。
式(39)的优化设计变量包含6个舱室几何形状参数(OP1与OP2形状相同,MP1与MP2形状相同,因此根据图3共有6个舱室几何形状参数)和32个压载水调节量参数(8个工况,每个工况4个压载水调节量),共38个参数,属于高维问题。此外,压载时间的求取依赖于对式(1)~(10)所描述的积分方程进行求解,这是典型的非线性问题;同时约束条件也不完全是线性的。可以认为,本文所建立的多目标优化模型是一个复杂优化问题。为了避免在其求解的过程中陷入局部最优,尽可能地在有限的计算资源下获得更好的优化结果,本文提出了一种多策略QPSO算法。下面对其进行描述。
3 多策略QPSO算法
3.1 QPSO算法
QPSO算法是一种针对PSO的改进算法。已经证明,QPSO相对于PSO具有更好的全局收敛性,适合求解复杂优化问题。在QPSO算法中,用波函数来描述粒子的运动状态,粒子在量子空间位置的概率密度函数可以由薛定谔方程得出,并使用蒙特卡罗方法模拟粒子的位置。假定QPSO中具有N个粒子,每一个粒子xk(1≤k≤N)对应于D维问题的一个解,且在第t次迭代时粒子位置可以表示为xk(t)=[xk,1(t),xk,2(t),...,xk,D(t)]。在第t+1代,粒子的位置更新公式为

式中,pk,d(t)是粒子k的局部吸引子的第d维,Lk,d(t)是粒子k的量子势阱长度的第d维,u是(0,1)之间均匀分布的随机数。pk,d(t)和Lk,d(t)的计算公式分别为

式(41)~(42)中,Pbestk,d(t)为粒子k的个体最优位置,Gbestd(t)为全局最优位置,φd(t)为(0,1)之间均匀分布的随机数,α(t)是收缩-膨胀因子,Mbestd(t)为所有粒子个体最优位置的平均值

3.2 QPSO的改进策略
尽管QPSO相比PSO有一些优点,但是在迭代过程中仍有可能陷入局部最优解。如果解空间比较复杂,局部最优解的数量较多,在迭代过程中种群多样性降低,那么就有可能出现过早成熟的现象。针对这些问题,提出了一种多策略量子粒子群算法(MSQPSO)。
3.2.1 最优个体多模式扰动策略
大量的实验观测表明,当所有粒子都与最优个体过于接近时,种群即有可能存在早熟停滞的风险。从这一事实出发,设计了一种针对最优个体Gbest的扰动策略:依次检测最优个体与其它粒子的距离δk(t),若δk(t)大于某一设定阈值,则基于最优个体生成扰动粒子Ptest,若Ptest的适应值F(Ptest)好于F(Gbest),则用Ptest更新Gbest。这种针对最优个体的扰动的目的在于,有可能将最优个体推向一个与其它粒子“保持距离”的位置,且这个位置的适应值更优,从而发挥最优个体在种群中的引领作用,同时降低早熟风险。
采用多种模式构造扰动粒子,即
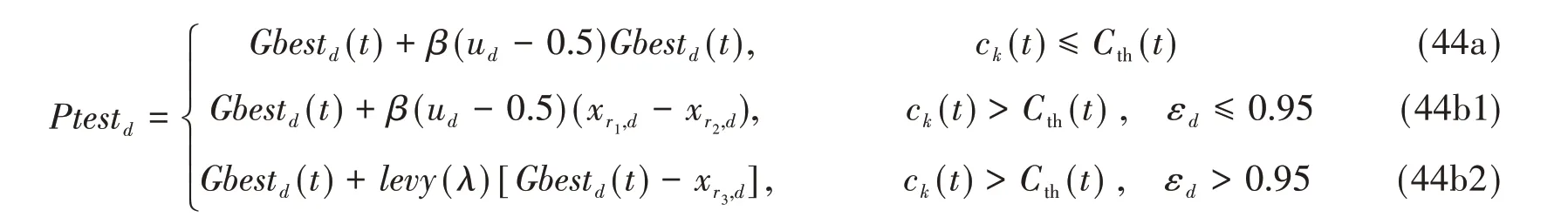
式中,r1、r2和r3是区间[0,D-1]之间的随机整数,β是位于区间[2.01,2.10]之间的实数,ck、ud、和εd是位于区间(0,1)之间均匀分布的实数,levy(λ)为符合Levy分布的随机步长,Cth(t)是动态调整的用于模式选择的阈值,按式(45)计算,

式中,la为过去L次迭代中按式(44a)生成的Ptest成功更新Gbest的次数,lb为过去L次迭代中按式(44b1)和(44b2)生成的Ptest成功更新Gbest的次数。L为评估窗口长度,可以取值为全部迭代次数的1/10。式(45)表明,会以更大概率选中绩优的扰动模式。
实际上,式(44)将扰动模式分为“自信息模式”(模式a)和“交互信息模式”(模式b)。对于模式a,扰动粒子的产生只使用了最优个体自身的信息;而对于模式b,扰动粒子的产生既使用了最优个体的信息,同时也使用了其它粒子的信息。模式b1和模式b2的区别在于:模式b1借鉴了DE算法的思想,属于一种基于差分的扰动;模式b2借鉴了Cuckoo算法中Levy飞行的思想,有可能产生频繁的小步长和偶尔的大步长,从而实现变尺度扰动。多模式扰动意义在于,个体行为的多样性有可能带来结果的多样性,从而降低种群的早熟停滞风险。
3.2.2 局部吸引子高斯扰动策略
在GAQPSO中,提出了一个针对粒子更新公式(40)的修正公式,即

式中,npk,d(t)~N[pk,d(t), |Mbestd(t)-Gbestd(t)|],为符合高斯分布的扰动局部吸引子。本文借鉴这一思想,对npk,d(t)做进一步修正,即设定npk,d(t)~N[pk,d(t),0.6 |Mbestd(t)-Gbestd(t)|]。这一修正在一定程度上缩小了高斯扰动的方差,以避免扰动范围过大反而带来无效搜索。
4 实验结果与分析
根据建造方提供的相关图纸和数据,4个立柱快速压载舱室未优化前8个工况的总压载时间为3 622 s,总压载水调节量为25 542 m3。本文采用PSO、QPSO、QPSO_RO、GAQPSO、DE、BBO、Cuckoo、ABC以及本文提出的MSQPSO等9种智能优化算法对式(39)所描述的优化目标函数进行求解。为保证算法比较的公平性和仿真结果的有效性,各算法的参数设置为:种群规模为100,自变量维度为38,最大迭代次数为2 000。每个算法运行50次,取平均值作比较。值得说明的是,Cuckoo、ABC和MSQPSO中每一次迭代中对目标函数的调用次数都大于种群规模,因此对这3种算法采取了限制迭代次数的处理,使它们的目标函数的总调用次数与其它算法持平。
9种智能优化算法的目标函数F(x)、总压载时间以及总压载水调节量的迭代过程如图4所示,图中每一代的结果均为50次运行的平均结果。表1给出了各算法50次运行的平均最优解。
根据图4和表1,可以得出以下结论:

表1 平均最优解Tab.1 Average optimal solution

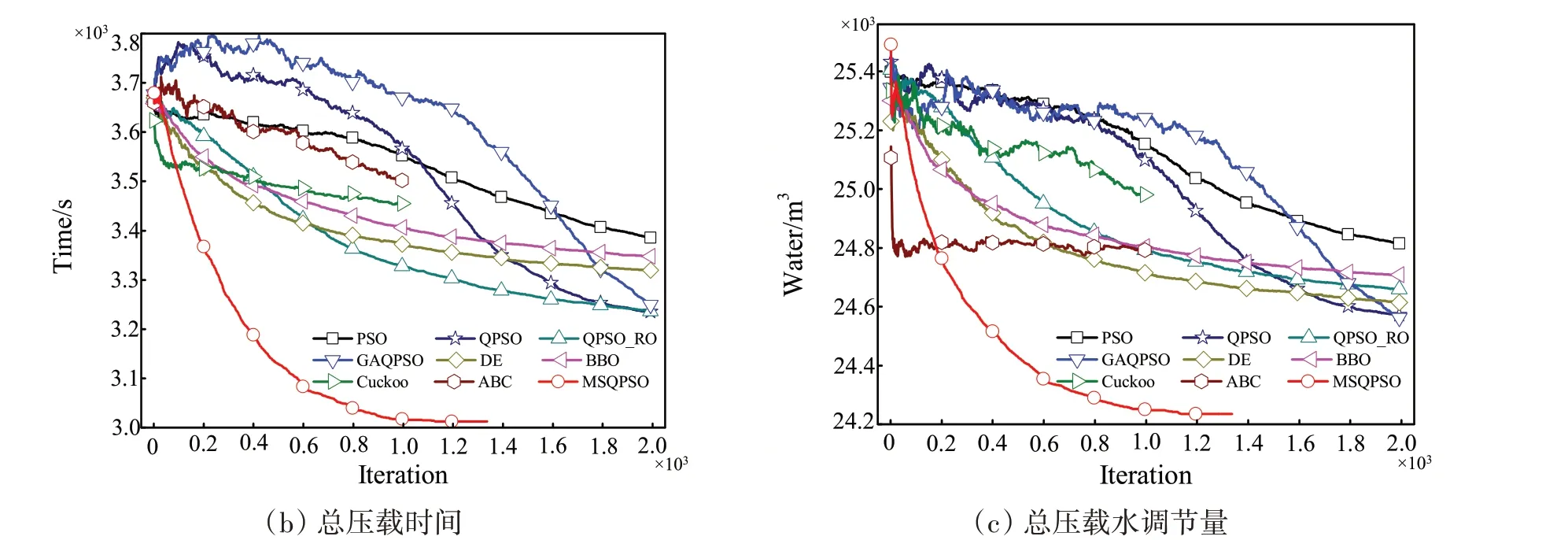
图4 迭代过程图Fig.4 Iterative process
(1)基于本文提出的多目标优化模型,9种智能优化算法均可以在不同程度上实现对压载时间和压载水调节量的优化。表明所提模型是合理的,有利于提高压载效率。
(2)对于本文的目标函数,新近提出的BBO、Cuckoo和ABC算法较之于PSO算法并未体现出明显的优势(Cuckoo和ABC甚至更差);DE算法的结果好于BBO、Cuckoo和ABC;而QPSO、QPSO_RO和GAQPSO相对于PSO和DE算法有一定的优势。
(3)通过迭代图可知,对于目标函数F(x)、总压载时间以及总压载水调节量,本文提出的MSQPSO在收敛速度和全局优化性能上都好于已有算法,并且优势非常明显。
综上,MSQPSO算法的优化结果最佳。该算法在平均意义上使8个典型工况的总压载时间减少了16.8%,总压载水调节量减少了5.1%。
5 结 语
本文以最小化8个典型工况的总压载时间和总压载水调节量为目标函数,以起吊过程中船体的倾角、稳性高、许用重心高度余量和舱室体积为约束条件,建立了半潜式起重平台立柱快速压载舱的多目标优化模型。提出了一种新颖的多策略QPSO算法——MSQPSO,用于对该模型进行求解,并将其与其它8种已有的智能优化算法进行了比较。计算结果表明,所提模型有助于提高半潜式起重平台快速压载系统的压载效率,且所提MSQPSO算法相对于已有优化算法具有较大的性能优势。在后续的研究中,将尝试将本文提出的模型和算法应用于其它海洋平台的优化设计。
