壁面结构形状对流体晃荡影响的数值研究
2021-10-11卫志军杜祥璞邹国良吴锤结翟钢军
卫志军,杜祥璞,邹国良,吴锤结,翟钢军
(1.大连理工大学a.海岸和近海工程国家重点实验室,b.航空航天学院,辽宁 大连 116023;2.南京水利科学研究院水文水资源与水利工程科学国家重点实验室,南京 210029)
0 引 言
中国的海洋油气资源储量丰富,向南海石油开发进军,是我国对南海海域实行管制的战略措施,还可以增加我国的石油产量和巨大的经济利益。浮式液化天然气(Floating Liquified Natural Gas,FLNG)终端具有开采周期短、可独立作业、可根据实际开采油气田生产状况灵活配置、无需管道输送、可回收和可运移等特点,非常适合我国南海深远海油气田开发[1]。特殊浮式开采平台的吨位和液舱容积越来越大,且无任何载液率限制,这不仅影响船舶的运动[2-3],导致流体对储舱结构产生较大的晃荡甚至砰击载荷,进一步引起舱壁结构强度失效,甚至浮式平台失稳[4-8]。因此如何合理有效地抑制储舱内流体晃荡是亟待解决的工程科学问题。
国内外学者针对如何抑制流体晃荡开展了一系列研究,主要采用在液舱内增设阻晃隔板或者在自由液面加设浮式装置的方式。在液舱内加阻晃隔板方面,Akyildiz等[9]研究了不同位置的压力分布以及3D效应对液体晃动的影响。薛米安等[10]通过实验在液舱中间加不同形式隔板并监测舱壁的冲击压力。Kandasamy等[11]数值模拟研究了三维液舱不同填装水平下,横向、斜向、常规、局部纵向和横向加速度作用下挡板设计的有效性。卫志军等[12]通过模型试验研究了近二维浅水条件下,液舱在大振幅简谐侧向激振作用和高固体率的垂直阻晃隔板作用下的砰击现象。Singal等[13]用数值模拟方法对煤油液体界面进行瞬态模拟,发现在燃料箱中引入挡板后,燃料箱内的晃动明显减小。对有内结构和无内结构的储罐进行了数值研究。蔡忠华等[14]数值讨论了强肋框、水平桁及制荡舱壁对于压力及液舱内液体固有频率的影响。在自由液面加设浮式装置方面,宁德志等[15]通过实验对三维液舱内柱型浮子式减晃结构的水动力特性开展了研究。Koh等[16]利用改进后的CPM成功地模拟了带约束浮动挡板(CFB)的水晃动。Yu等[17]在六自由度运动平台上的刚性矩形液舱内进行了不同固体率的双穿孔浮板抗晃动模型的扫频试验。Jithu等[18]基于RANSE数值模拟研究了有球型浮动挡板和无球型浮动挡板情况下的储罐结构变形和储罐壁面压力。李雪艳等[19]考虑波面高程、透射系数、反射系数、能耗系数及耗散波能等指标,对平板式、上弧板式和下弧板式三种透空堤开展了消浪性能数值研究。
由于上述两种抑制方式均对工艺要求甚高,在实际建造过程中较难实现[15,20-21]。真实船载LNG液舱的建造中,法国GTT公司设计的液化天然气储舱MARKIII表面具有凸起结构。从壁面结构自身结构特性开展流体晃荡抑制可以满足建造工艺,有利于工程实现。然而国内外针对壁面凸起结构抑制流体晃荡影响的研究较少。Graczyk等[22]通过实验方法分析在二维模型低液位的工况下凸起结构对流体晃荡荷载的影响,研究表明凸起物使流体冲击壁面时引入大量空气,并且水平凸起物下面的压力比上面的更大。Moirod等[23]采用数值方法对比分析一个光滑的楔形体和一个凸起结构的楔形体的入水砰击试验,结果表明凸起结构可以增大晃动压力,建议设计超大型船载储舱时,需考虑凸起结构对砰击的影响。目前尚未有针对壁面凸起结构抑制流体晃荡的系统研究。为此,本文采用数值方法,从物理机理角度系统分析三种不同形状凸起结构对流体晃荡的抑制效果。结果表明,合理设计凸起结构能够改变流体砰击模式,有效降低晃荡荷载冲量,进而有效抑制流体晃荡。该研究结果能为储舱抗砰击设计提供科学参考。
1 计算模型参数
矩形液舱模型尺寸及波高与压力测点如图1所示,模型尺寸长(L)1 m、高(H)1 m、宽(B)0.1 m,壁面凸起块凸起高度0.05 m,与舱壁接触面为边长0.05 m的正方形,采用ICEM软件建模、结构化网格和FLUENT计算。通过文献调研得知,在流体晃荡过程中气体的气垫效应是不可忽略的因素[24-25]。因此本文考虑气体可压缩性,采用VOF模型对自由液面进行捕捉[26-28],湍流模型选择Standardk-ε模型,计算参数设置如表1所示。

表1 数值模拟参数设置Tab.1 Numerical simulation parameter settings

图1 矩形液舱尺寸示意图(单位:mm)Fig.1 Schematic diagram of rectangular tank size(Unit:mm)
2 网格无关性检验
本文采用二维模型,分别针对5种网格进行无关性检验,参数设置如表2所示,时间步长为0.001 s。考虑到浅水工况下,流体运动较剧烈,因此设计h/H=0.125,h为载液高度。激励形式采用单自由度正弦激励,
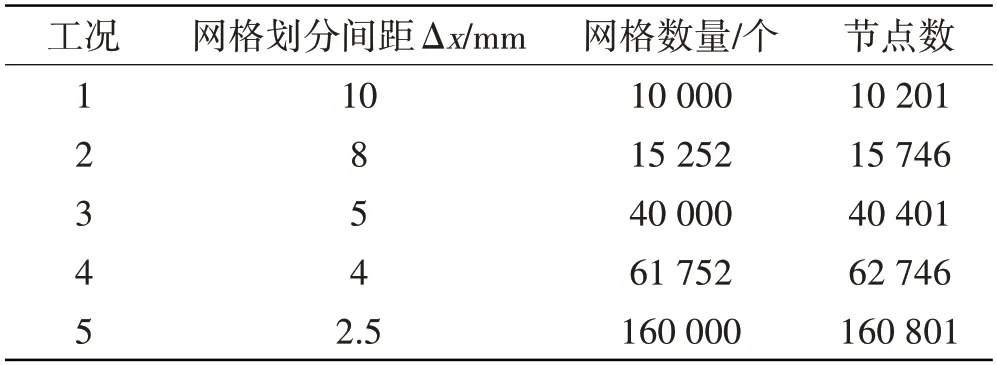
表2 网格无关性计算工况Tab.2 Grid independence calculation condition

式中,A为激励幅值,f为激励频率,t为激励时间。网格无关性检验中,A为0.1m,f/f0=0.74,f0为自由液面最低阶固有频率。通过对比晃荡荷载和近壁面波高发现,当网格增加到工况3时,计算结果已经趋于收敛,如图2所示。

图2 网格无关性检验Fig.2 Grid independence test
进一步分析计算误差,

式中,η为压力峰值或波高峰值,i=1,2,3,4。分析结果见表3。

表3 误差分析Tab.3 Error analysis
综合考虑计算时间与精度,二维情况下工况3网格间距满足计算要求,因此本文选择网格间距为5 mm开展后续研究。
3 数值可靠性验证
为了保证数值方法的可靠性,本项目在大连理工大学工业装备及结构分析国家重点实验室开展了相关模型试验研究,将数值结果与实验结果进行系统对比,校核数值模型。实验液舱模型见图3(a),压力测点见图1。由于流体非线性影响[29-30],结果的峰值稍有差别,但在晃荡荷载趋势和量级方面吻合较好,如图3(b)所示,因此本次数值方法可用于后续研究工作。
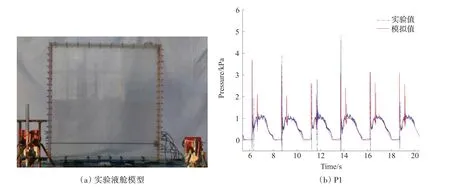
图3 数值模拟与实验压力结果对比,h/H=0.125,f/f0=0.74Fig.3 Comparison of numerical simulation and experimental pressure results,h/H=0.125,f/f0=0.74
4 结果与讨论
本文属于概念设计初步研究工作,仅在二维情况下讨论单一壁面结构对流体晃荡的影响。考虑到流体晃荡的能量主要分布在自由液面最低阶固有频率附近,因此数值试验的无量纲激励频率f/f0分别为0.8、1和1.2。激励函数如式(1),载液率为0.125,激励振幅为0.1 m。本文以三种不同壁面结构的形状(三角形、梯形、正方形)为变量,并以光滑壁面作为对照试验,从时间和空间分布方面系统分析壁面结构形状对晃荡荷载的影响,最后分析其对波高的影响。
4.1 壁面结构形状对晃荡荷载时间分布的影响
为了细致分析壁面结构形状对流场的影响,根据凸起结构的位置,将左侧舱壁分成上下两个区域,如图4所示,分别从上和下区域各选择一个具有代表性的测点P2和P3。在最低阶固有频率附近,具有四种不同壁面结构形式的液舱中压力时程曲线对比如图5所示。

图4 上部区域和下部区域Fig.4 Schematic diagram of upper and lower regions


图5 压力时程对比Fig.5 Comparision of the pressure time histories
对于下部区域P2测点,流体冲击具有壁面凸起结构时,壁面晃荡压力表现为双峰,如图6所示,且流体砰击的第一个峰值较尖锐,持续时间较短。此外,不同形状的凸起结构下的压力均大于光滑壁面压力:当激励频率f/f0=0.8时,梯形凸起结构压力峰值最大,约为相同工况下光滑壁面压力的5倍;当激励频率f/f0=1时,三角形凸起结构压力峰值最大,约为光滑壁面的1.5倍;当激励频率f/f0=1.2时,梯形凸起结构压力峰值最大,约为光滑壁面3倍。产生上述现象的原因将在后续给出。然而,光滑壁面工况中由于重力引起的第二个压力峰值均大于具有壁面结构工况中的压力,且随着频率的增大,差距越显著。分析认为由于凸起结构的存在,使得流体能量损耗增加,流体动能转化为势能减少,流体沿着壁面爬高降低,进而导致流体晃荡的第二个压力峰值下降。此外,在流体沿着壁面向上爬升过程中,需绕过壁面凸起结构作用到上部区域,这一过程导致同一周期内有壁面凸起结构时的压力峰值比光滑壁面在时间上发生得晚,导致压力时程曲线具有一定的相位差。

图6 压力双峰曲线Fig.6 Pressure bimodal curve
从上部区域P3测点的峰值看,受凸起结构的影响,流体对上部区域作用力均有所下降,在f/f0=1和f/f0=1.2时降低较为明显。所以对于下部区域,壁面凸起结构引起测点压力第一个峰值上升,第二个峰值下降;对于上部区域,壁面结构均会促使流体对舱壁的作用力显著下降。
通过压力时程对比,为了深入分析壁面结构抑制流体晃荡的物理机理,针对半个周期内自由液面和晃荡荷载的演化过程,针对代表性的具有矩形凸起结构的壁面与光滑壁面工况开展细致分析。当f/f0=0.8时,光滑壁面液舱半个周期内的流场随时间变化如图7所示,液舱从原点向左运动,液舱内一列行波向左侧壁面传播(图7(a)#1),该行波具有显著的水头,随着左侧壁面附近波谷向上抬升,水头高度逐渐减低,流体直接冲击到壁面约0.08 m处(图7(a)#2),凸起下部区域形成了由于砰击产生的第一个峰值(图7(c)#2),且此时流体尚未到达上部区域(图7(d)#2)。随着液舱运动到左侧最大位移处,液舱运动速度逐渐降低到0,由于惯性力的作用,流体沿壁面向上爬升(图7(a)#3)直至动能全部转化为势能,流体运动到垂向最大位置。随后,流体在重力作用下,开始回落,即势能逐渐转化为动能,下部区域形成压力双峰曲线的第二个峰值(图7(c)#4),而由于大部分流体已离开上部区域,因此上部区域在重力作用下的流体作用力较小(图7(d)#4)。当液舱反向运动,流体也向右侧舱壁传播,如图7(a)#5和#6所示。


图7 半周期内,f/f0=0.8工况下光滑壁面流场变化Fig.7 Flow evalution during half cycle for smooth wall surface subjected to f/f0=0.8
考虑到对流体晃荡的抑制效果,本文选择效果较好的正方形凸起壁面流场随时间变化进行分析,液舱位移与半个周期内的流场随时间变化如图8所示,液舱从原点向左运动,液舱内一列行波向左侧壁面传播(图8(a)#1)。当流体冲击到左侧壁面被凸起结构分割成两部分时,下层流体受阻挡被困在液舱底面与凸起结构之间,并与凸起结构围成一个大的封闭气腔(图8(a)#2),流体通过压缩空气作用在壁面上,形成压力双峰曲线第一个峰值(图8(c)#2),正是由于形成气腔导致凸起结构第一个压力峰值比光滑壁面第一个压力峰值提前约0.02 s,这说明壁面凸起结构可以延长下部区域荷载作用时间。随着液舱速度下降,上层流体冲击到正方形壁面凸起结构,其运动方向和自由液面形状发生了比较大的变化。水头跃起到半空(图8(a)#3)(三角形和梯形凸起结构下流体产生翻卷现象),此时压力在双峰之间波谷处(图8(c)#3)以静水压力为主,而发生水跃将直接导致上部区域壁面凸起结构压力峰值比光滑壁面在时间上发生得晚。在(图8(a)#4)中液舱速度为0时,流体受重力影响开始回落形成压力双峰曲线的第二个峰值(图8(c)#4)。
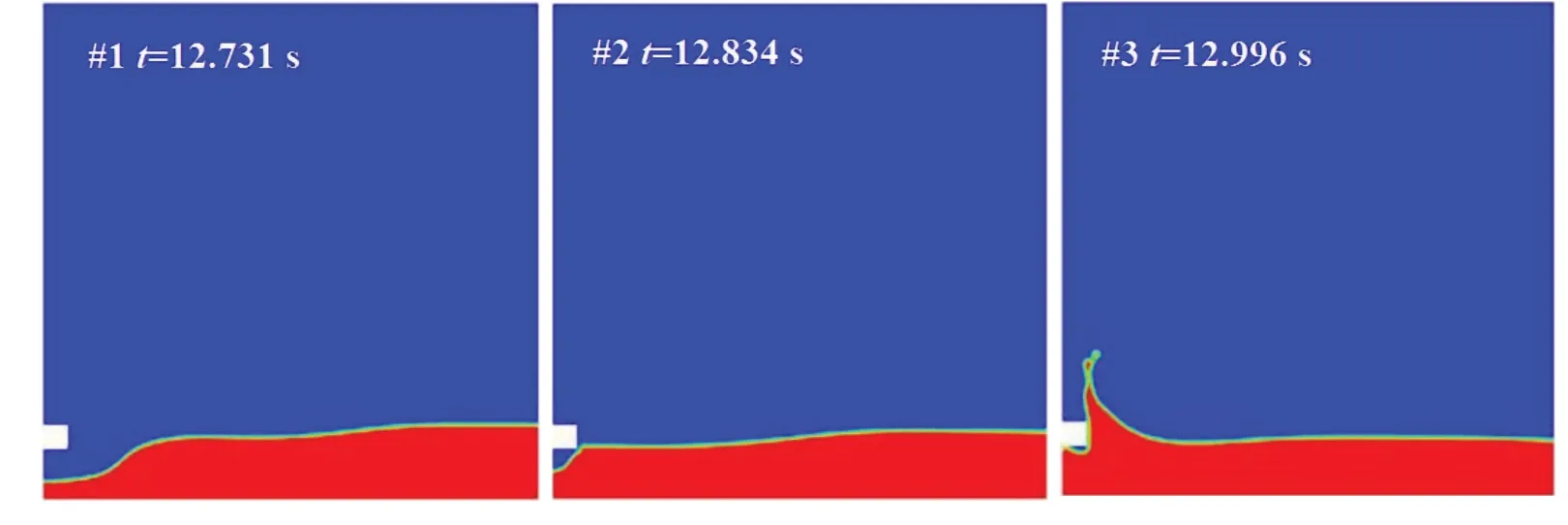
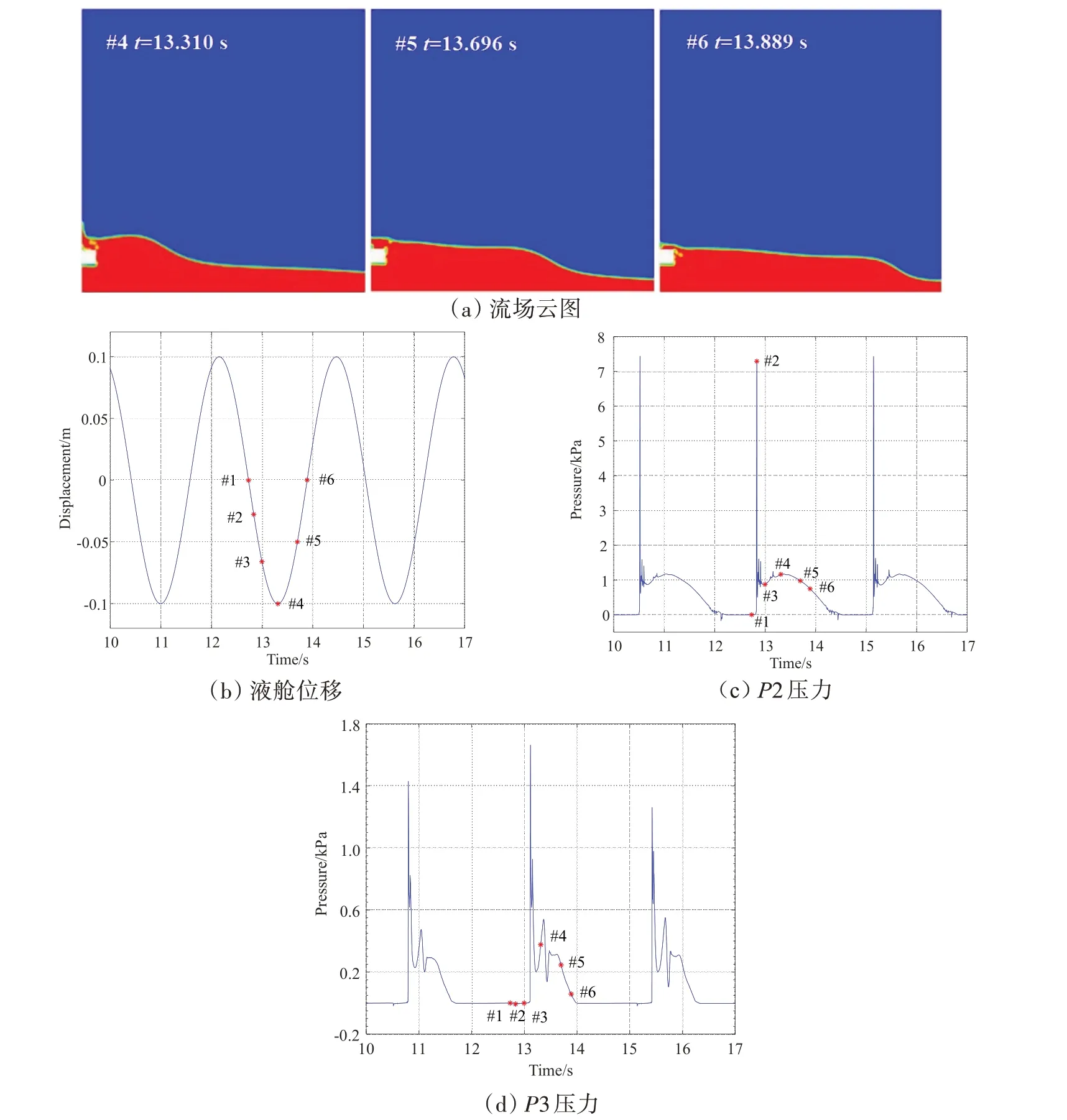
图8 半周期内,f/f0=0.8工况下正方形凸起壁面流场变化Fig.8 Flow evalution during half cycle for square raised wall surface subjected to f/f0=0.8
通过对流场冲击过程中自由液面物理现象的分析,发现添加壁面结构改变产生最大砰击荷载的原因:流体直接砰击光滑侧壁,产生最大的砰击荷载(图7(a)#2),转为气体,在流体挤压作用下,转而作用具有壁面结构的侧壁,产生最大砰击荷载(图8(a)#2)。针对图7#2和图8#2流场瞬态空气密度分布(图9)开展分析,发现空气密度分布在水平方向上越接近左侧壁面,密度越大;竖直方向上越接近自由液面密度越大,在凸起结构下侧与壁面接触点密度达到最大。

图9 不同形状凸起结构空气密度分布Fig.9 Air density distribution of convex structure with different shapes
当流体到达壁面,受惯性作用和竖直液舱壁的影响有向上爬升的趋势,光滑壁面冲击位置附近空气扩散和流体向上爬升不受阻碍。相反地,由于凸起结构阻碍了流体向上爬升,即凸起边界对流体产生了挤压作用。由于空气可压缩性,从空气密度云图来看,相对于光滑壁面,壁面结构冲击位置处气体密度较大,说明空气被压缩,同理液体也受挤压。此时流体受挤压的力会反作用于壁面,从而导致该区域的壁面压力增加。从另一个角度分析,空气被局部压缩必然导致该区域气体压力增加,相当于凸起结构下部区域受到了较大的局部气压,该局部区域的绝对气压大于整个液舱所处环境的气压。因此,无论是空气和水直接受到向上的阻碍还是空气被压缩,都是壁面凸起结构的下壁面压力增加的原因。
当砰击发生后,壁面凸起结构对流场湍动能的影响如图10所示。湍动能主要集中于凸起结构附近,即凸起结构是导致流场湍流增强的主要原因。湍动能的增加引起了动能耗散的增加如图11所示,添加壁面凸起结构时湍动能耗散率显著提高,所以砰击发生后,由于结构的存在导致能量消耗,从而使得流体晃荡荷载降低。这是导致凸起结构下部区域第二峰值和上部区域压力相对于光滑壁面下降的主要原因。

图10 不同形状凸起结构湍动能Fig.10 Turbulence kinetic energy of convex structure with different shapes

图11 不同形状凸起结构湍动能耗散率Fig.11 Turbulent dissipation rate of convex structure with different shapes
4.2 壁面结构形状对晃荡荷载空间分布的影响
4.2.1 晃荡压力空间分布
考虑到晃荡荷载的不确定性,本文采用5个周期压力峰值的平均值分析壁面结构形状对晃荡压力空间分布的影响,如图12所示。随着激励频率的增加,流体冲击壁面的位置逐渐提高。随着冲击位置的变化,凸起结构的形状对荷载的影响敏感度较大。从整体来看凸起结构对上下两个区域影响结果相反,即凸起结构会引起下部区域产生较大的局部压力,而上部区域的压力则相对于光滑壁面有所下降。

图12 晃荡压力峰值平均值空间分布Fig.12 Spatial distribution of the mean value of the sloshing pressure peak
4.2.2 晃荡荷载冲量空间分布
考虑到液舱的安全性,结构响应是不可忽略的,相比于瞬间较大的局部压力,持续的压力作用,即晃荡荷载冲量,才是影响结构响应的重要因素。本文通过计算冲量I评价不同液舱中砰击压力的动力特性和其空间分布,

式中,t1和t2分别代表砰击前、后的时间,p是由于砰击产生的局部压力。
冲量为压力曲线下的红色阴影面积,如图13(a)所示。当f/f0=0.8时,壁面凸起结构对下部区域影响不明显,导致上部区域冲量下降较大;当f/f0=1时,壁面冲量相对光滑壁面下降均较明显,在上部区域冲量甚至下降一半以上;当f/f0=1.2时,壁面凸起结构工况中下部区域冲量下降明显,上部区域梯形和正方形凸起结构可以引起冲量下降,而三角形凸起结构超过了光滑壁面冲量。从这三种不同频率工况来看,激励频率f/f0=1时,壁面结构可以更有效抑制流体晃荡。综上所述,采用壁面结构形状抑制流体晃荡是行之有效的方法。但需设计合理的壁面凸起结构形状,以有效降低荷载冲量,从而抑制晃荡。


图13 冲量空间分布对比Fig.13 Comparison of impulse spatial distributions
4.3 壁面结构对波高的影响
本文选取稳定状态波高时程数据进行分析,各个周期波峰值标准差数量级很小,如表4所示,说明峰值波动较小,可以对峰值进行平均分析。差值计算公式为

表4 不同壁面结构的波高平均峰值Tab.4 Average peak of wave height of different wall structures

式中,h0为光滑壁面波高平均峰值,hi为有凸起结构壁面波高平均峰值,i=1,2,3分别代表三角形、梯形和正方形凸起壁面。
不同壁面结构波高曲线趋势基本一致,波高峰值的第二个峰值大于第一个峰值,如图14所示。


图14 自由液面高度对比Fig.14 Comparison of wave heights
本文以一个周期内波高最大值,即第二峰值为分析对象。激励频率f/f0=0.8时,壁面凸起结构对波高的抑制比较明显;激励频率f/f0=1时,壁面结构对波高依然具有一定的抑制效果,但是抑制效果较低频率有所下降;激励频率f/f0=1.2时,由于加壁面凸起结构自由液面破碎较严重,波高反而增大了。结果表明,在最低阶固有频率及其以下低频率,壁面凸起结构对波高有抑制作用,随着频率的增加抑制作用有下降趋势。当频率高于最低阶固有频率时,壁面凸起结构可导致波高的增加。
5 结 论
本文采用数值方法,系统分析了不同形状壁面结构形状对流体晃荡的影响,主要结论如下:
(1)壁面凸起结构改变了流体砰击模式。
(2)流体从直接砰击壁面变为包裹气泡间接砰击壁面,因此气泡的产生影响了晃荡荷载的时空分布及其冲量和波高,并增强流体能量耗散。由此可见,气体可压缩性是研究流体晃荡需考虑的重要因素之一。
(3)合理设计壁面结构的形状可以有效地抑制晃荡,未来将系统研究不同载液率、凸起结构数量以及自由液面与凸起结构相对位置对流体晃荡的影响等问题。
