具有捕获的反应扩散浮游生物模型的动力学行为

张真真, 李盈科, 唐生雨

(新疆农业大学 数理学院, 新疆 乌鲁木齐 830052)

0 引言

浮游生物泛指生活于水中而缺乏有效移动能力的漂流生物,其中分为浮游植物及浮游动物．浮游植物不仅是所有水生食物链的基础,而且还可以产生70%的大气氧气、吸收一半的二氧化碳.浮游动物摄食浮游植物位于水生食物链的第二营养层．浮游生物是水域生产力的基础,浮游植物的产量又决定着浮游动物的产量,后者又是鱼类和其他水生动物最有利的食物来源．因此,渔获量的大小基本上取决于浮游生物产量．由于浮游生物在理论上和实践上的重要性,许多学者对浮游植物与浮游动物构成的系统进行了大量的研究[1-2]．

近20年来,全球有害浮游生物大量繁殖,造成了巨大的社会经济破坏[3-4]．有害藻华是指通过产生自然毒素、机械损伤或其他方式对其他生物体造成负面影响的藻华．此外,浮游植物释放有毒物质不是一个瞬时过程,而是由该物种成熟所需的时间延迟导致的,时滞系统导致了时滞微分方程. 这一问题已经得到了深入系统的研究,并展示了丰富的动力行为．例如，Wang Y等[5]提出并研究了一种具有延迟和选择性捕获的有毒浮游植物和浮游动物模型．Li J等[6]为了研究浮游植物产生的毒素和浮游植物的栖息地对浮游植物-浮游动物相互作用的影响,建立了一个简单的具有Holling II型功能反应函数的浮游植物-浮游动物系统．Shi R X等[7]以两种浮游动物妊娠延迟为参数,研究了两种浮游动物-浮游植物动力学模型．但是这些模型是关于时间变量的微分方程,忽略了空间效应．浮游生物可以通过扩散和水流在湖泊和海洋中移动,因此,研究空间变化对模型的影响也是非常有必要的．许多作者通过反应扩散方程模拟了浮游植物和浮游动物种群的空间变化[8-9]．Zhao J等[10]研究了具有延迟和有毒物质产生的浮游生物反应扩散系统的动力学行为;Zhichao J等[11]研究了一个具有时滞和反应扩散项的浮游植物-浮游动物系统;Li Y等[12]提出了一个具有扩散的浮游植物浮游动物模型,其中也考虑了浮游动物捕食的时间延迟和浮游动物捕获．

本文建立了一类具有捕获的反应扩散浮游生物模型, 分析了平衡点的存在条件；证明了系统在无时滞时解的正性和有界性.通过运用上下解的方法证明了边界平衡点的全局渐近稳定性,通过求解特征方程的特征根得到灭绝平衡点和正平衡点的局部稳定性以及Hopf分支的存在条件．最后，通过数值模拟验证了结论．

1 模型与平衡点

首先，给出具有捕获的反应扩散浮游植物-浮游动物相互作用模型(1)如下:

(1)

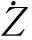
令Ω=(0,π),|Ω|表示水域的深度,其次Neumann边界条件意味着没有浮游动植物进入或离开水域的上下边界．当τ=0时,模型(1)转化为如下模型:

(2)

其中φ1(x)=φ1(x,0),φ2(x)=φ2(x,0)．系统(2)的平衡点满足如下方程组

易得灭绝平衡点E0(0,0)和边界平衡点E1(P1,0),并且P1满足方程

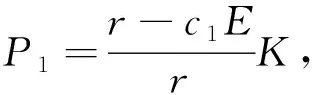
对于正平衡点E*(P*,Z*)满足

解得

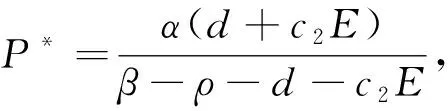
令

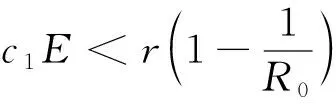
2 解的正性和有界性

定理1 1) 若φi(x,t)≥0且φi(x,t)≠0(i=1,2),则系统(2)有唯一解(P(x,t),Z(x,t)),且满足

00,x∈Ω,

其中(P*(t),Z*(t))是下面方程的唯一解

2) 对于系统(2)的所有解(P(x,t),Z(x,t))，有

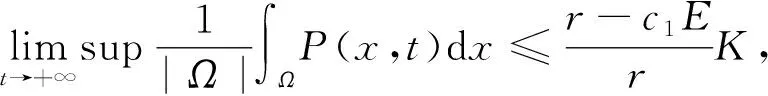
证明定义

当β>ρ时,

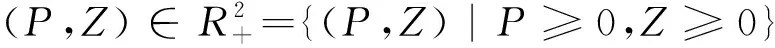
令(P1(x,t),Z1(x,t))=(0,0),(P2(x,t),Z2(x,t))=(P*(t),Z*(t)),由于

所以(P1(x,t),Z1(x,t))=(0,0),(P2(x,t),Z2(x,t))=(P*(t),Z*(t))分别是系统(2)的下解和上解,由文[13]中定理4.3.3,可得系统(2)存在唯一解(P(x,t),Z(x,t))，且满足

0≤P(x,t)≤P*(t),0≤Z(x,t)≤Z*(t),t≥0,x∈Ω,

由强最大值原理可得,当t>0时,对所有的x∈Ω有P(x,t)>0,Z(x,t)>0，证毕．

由上面的讨论可知,对所有的t>0,P(x,t)≤P*(t)且P*(t)是方程

的唯一解,并且可得方程的通解为

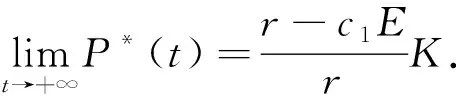
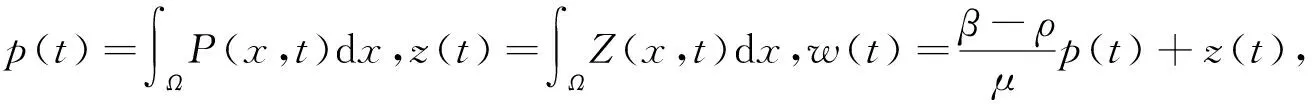
通过使用Neumann边界条件, 可以得到

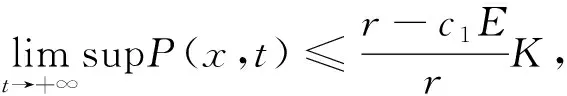
易得微分方程

的解w(t)满足

由比较原理得,存在T3>T2,当t>T3时,有

则推出

于是

证毕．

3 系统的稳定性和分支

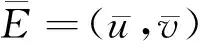
(3)

其中

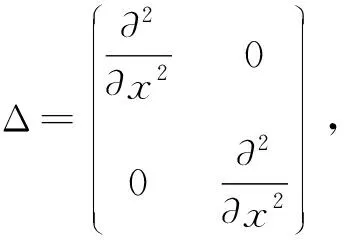
这里

(4)

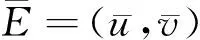
(5)

其中

特征方程为

(6)

其中y∈dom(Δ){0},dom(Δ)⊂X,并且

eλ.(θ)y=eλθy,θ∈[-τ,0] ,

因为特征问题

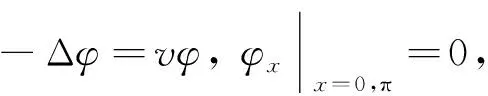
有特征值

v=k2,k∈Ν0=Ν∪{0},

对应的特征函数为cos(kx),k∈Ν0．对式(6)使用傅里叶级数展开得

(7)

其中ak,bk∈C．因此特征方程(6)等价于

定理2 当c1Er时,灭绝平衡点E0(0,0)局部渐近稳定．

证明系统(1)在平衡点E0(0,0)线性化,得

其对应的线性化矩阵为

对应的特征方程为

即

[λ+d1k2-(r-c1E)][λ+d2k2+(d+c2E)]=0,k∈Ν0,

特征值为λ1=-d1k2+(r-c1E),λ2=-d2k2-(d+c2E)]<0．当c1E0．此时平衡点E0(0,0)不稳定;当c1E>r时,对所有的k∈Ν0,都有λ1<0,此时平衡点E0(0,0)局部渐近稳定．

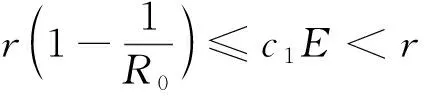
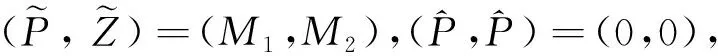
因为

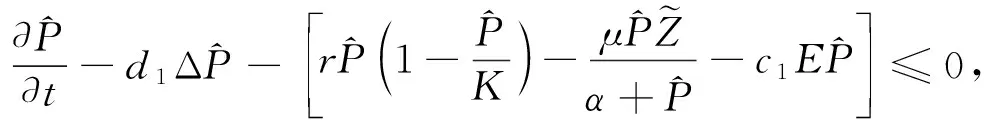
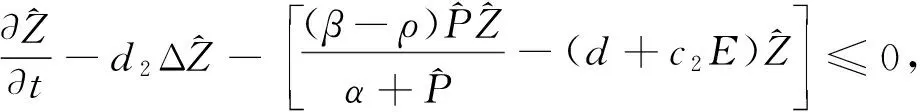
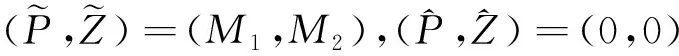
(0,0)≤(P,Z)≤(M1,M2),

此时(0,0)≤(φ1(x,t),φ2(x,t))≤(M1,M2)．当φi(x,t)不恒等于0,i=1,2时,

P(x,t)>0,Z(x,t)>0,t>0,x∈Ω,

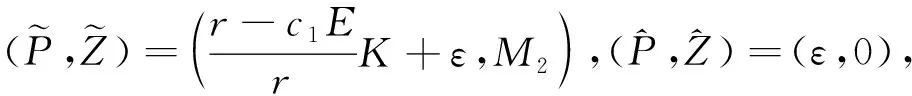
定义如下两个序列:

(8)

所以

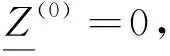
对式(8)两边取极限,可得

(9)

由拋物型边值问题的比较原理,可得

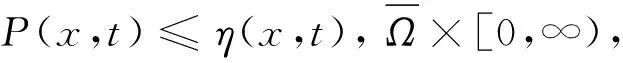
其中η(x,t)是下列方程的正解

(10)

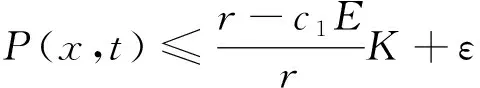
平衡点E1(P1,0)的吸引性得证.

下面证明平衡点E1(P1,0)的局部渐近稳定性．在平衡点E1(P1,0)处线性化，得

(11)

其中

特征方程为

即

特征值为

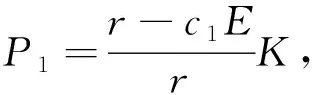
下面讨论平衡点E*(P*,Z*)的稳定性．在平衡点E*(P*,Z*)处线性化得

(12)

这里L:K→X定义为L(φt)=L1φ(0)+L2φ(-τ),其中

特征方程为

即

λ2+Mkλ+Nk+De-λτ=0

(13)

其中

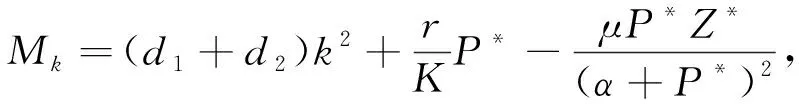
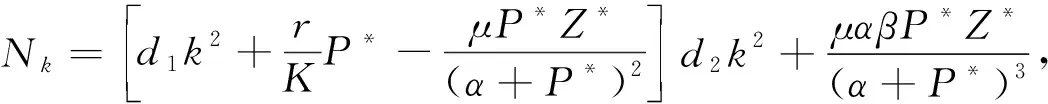
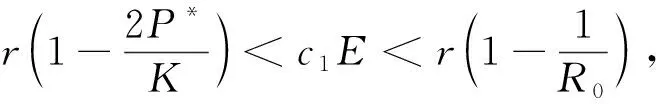
证明当τ=0时,特征方程为

λ2+Mkλ+Nk+D=0,

所以

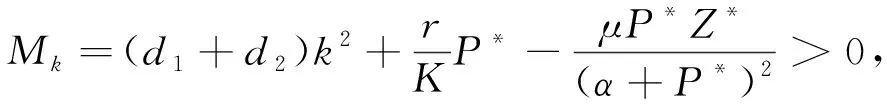
所以特征根全部有负实部,因此平衡点E*(P*,Z*)是局部渐近稳定．

当τ>0时,寻找一个临界值使得特征方程存在一对纯虚根,令±ωi(ω>0)为特征方程(12)的解,则有

-ω2+Mkωi+Nk+De-iωτ=0,

由欧拉公式e-iωτ=cosωτ-isinωτ分离实部和虚部,得

(14)

由sin2ωτ+cos2ωτ=1得到

令z=ω2,则上式化为

(15)

其中

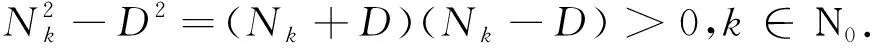
由于

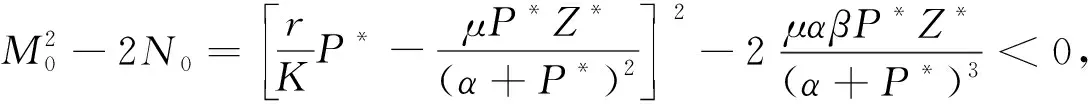
并且

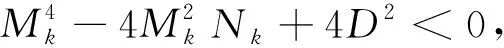
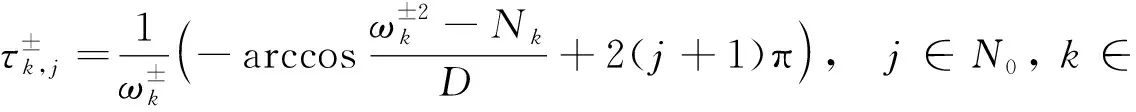
(16)

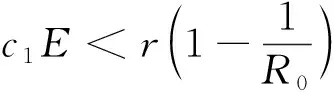
证明将特征方程λ2+Mkλ+Nk+De-λτ=0两端对τ求微分得

则

所以

证毕．

由方程(16),可得

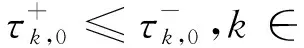
定义使得稳定性发生变化的最小τ,

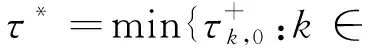
通过以上分析并由文[15]中推论2.4可得下面的引理．

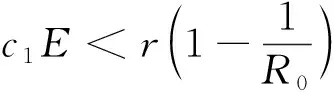
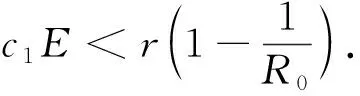
4 数值模拟

令Ω=(0,π),r=0.02,K=3,μ=0.3,α=0.5,β-ρ=0.15,d=0.04,c1=0.3,c2=0.1,E=0.1,d1=d2=0.02,这些参数满足定理2的条件c1E>r,灭绝平衡点E0(0,0)局部渐近稳定(图1)．

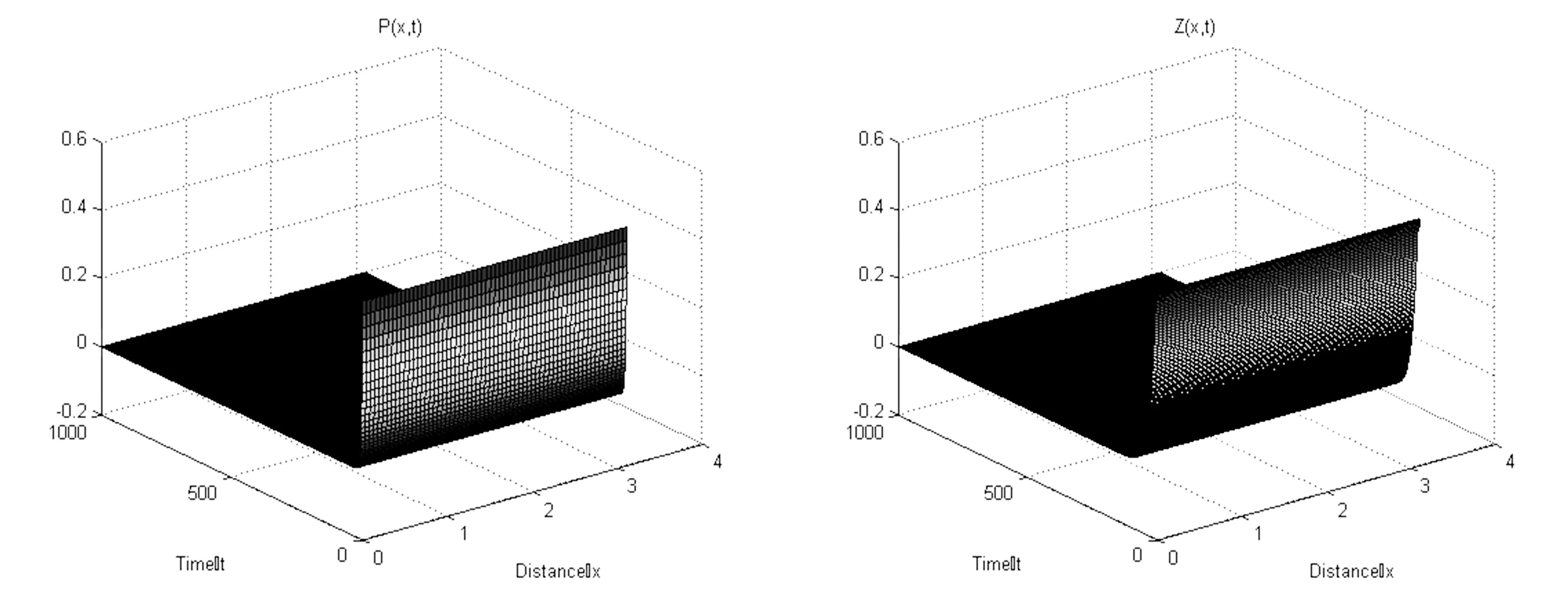
图1 灭绝平衡点E0(0,0)局部渐近稳定

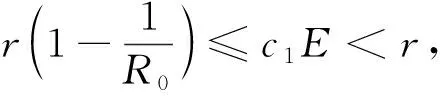
图2 边界平衡点E1(2.82,0)全局渐近稳定

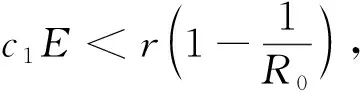
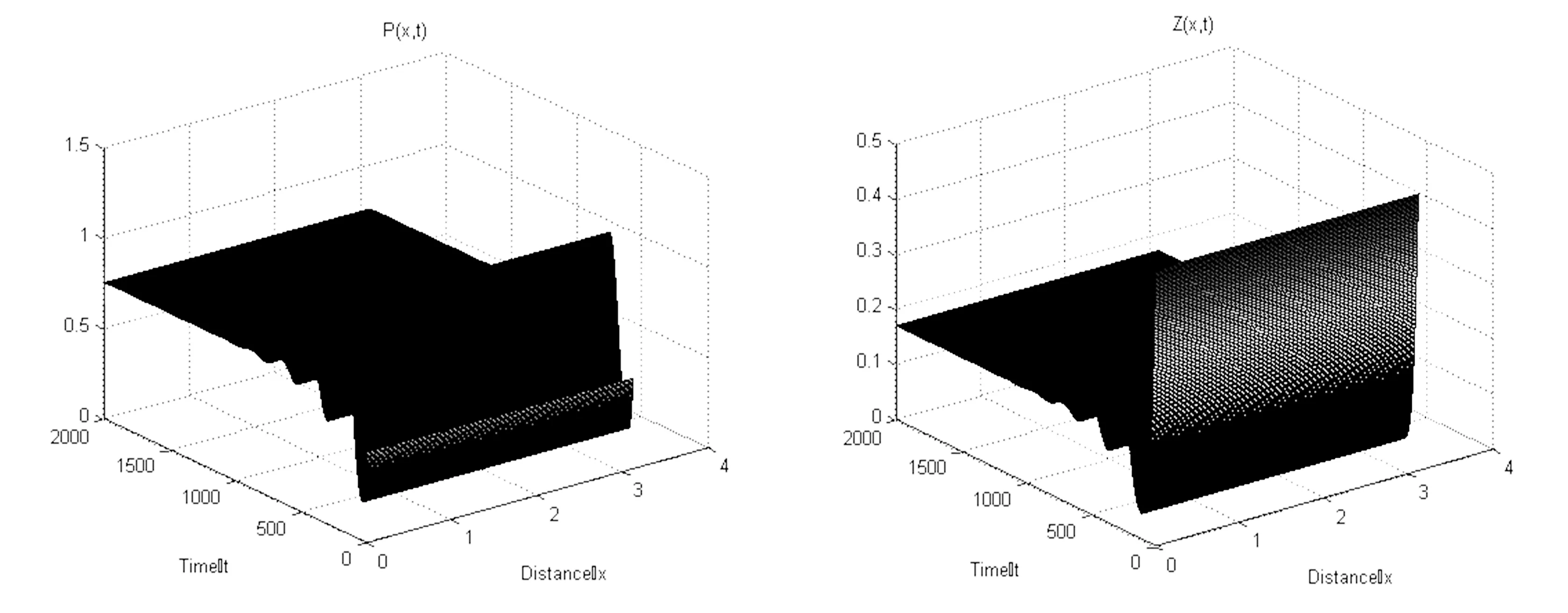
图3 正平衡点E*(0.75,0.16875)局部渐近稳定