微分几何中向量的Levi-Civita平行移动

栗嘉慧, 何 勇, 邓香香, 肖 维

(新疆师范大学 数学科学学院, 新疆 乌鲁木齐 830017)

0 引言

微分几何的核心是关于流形上黎曼度量的研究，即黎曼几何[1].Levi-Civita意义下的平行性是研究黎曼几何性质的重要概念，最早由Levi-Civita于1917年在讨论三维欧氏空间中的曲面时提出.1918年，Weyl[2]受其中所蕴含几何思想的启发，引入了不依赖于任何一个黎曼度量的一般联络的概念，并用它阐释了Levi-Civita平行移动，给出了Levi-Civita联络一个恰当的表示形式.近年来，许多学者对Levi-Civita平行移动进行了相关研究，Ruta[3]和Iurato[4]讨论了分析力学的虚功原理在推导Levi-Civita平行移动概念中所起的关键性作用.2016年，Casey[5]构造了一种特殊标架，即Levi-Civita标架，并给出了可展曲面上的相关结论.联络是对流形上向量场进行“微分”的一种手段，而Levi-Civita平行性正是切丛上的联络[6]，因此，理解Levi-Civita平行移动这一概念尤为重要.本文旨在通过三个方面阐释Levi-Civita平行移动的内涵，从而帮助初学者更好地学习和理解这一概念，即采用直观的向量投影的方法分析向量的Levi-Civita平行移动；利用平移同构探析Levi-Civita平行移动与联络的内在关系；对比Levi-Civita平行移动与欧氏平移基本性质的异同.

1 Levi-Civita平行移动的概念

1.1 二维曲面上向量Levi-Civita平行移动的概念

平面上向量沿直线平移具有两个重要特征,其一是该向量的微分为0;其二是该向量与直线所成夹角在平移过程中不发生改变.在古典微分几何中,对于二维曲面,若将其上向量v从点Q沿曲面上一曲线按上述平移移动至邻近点Q′,则v一般不再是曲面上的向量,曲面上的向量是指曲面上给定点处切于此曲面的向量[8].因此,一个较关键的问题是,如何将平面上向量平行移动的概念推广到曲面上.

在探讨曲面上向量沿曲线平移之前,首先将这条曲线无限分割,从而问题转化为向量沿无穷小弧段的平移,又因“无穷小”这一概念与“微分”联系紧密[9],所以势必要考虑在曲面上如何对一个向量进行微分.为此,介绍一种新的“微分”,它满足以下两个性质:对上述向量v微分为0;v经过平移后仍是曲面上的向量.

v设在曲面上沿曲线C有一向量场v,则对C上任意一点Q都有一确定向量v.将v沿C向邻近点Q′平移得到v,再将v分别向切平面和法方向做投影,点Q与Q′的切平面间的微小角度忽略不计,则n沿切平面的分量可以表示为v-(n·v)n,即v+dv-(n·dv)n,称其与原向量v的差dv-(n·dv)n为v沿曲线C的绝对微分,记为Dv[8].事实上,表达式dv-(n·dv)n表明绝对微分就是增量dv在切平面上的投影,所以绝对微分仍是曲面上的向量.

接下来,基于平直空间中向量经过平移其微分为0这一性质,思考绝对微分为0,即Dv=0的两层含义.其一是通过绝对微分的表达式得到dv=(n·dv)n,该等式表明由平移产生的增量dv沿法方向;其二是利用n沿切平面的分量表达式v+dv-(n·dv)n,得到n沿切平面的分量就是原向量v.这两种含义都直接表明:在不考虑法方向分量的情况下,向量v经过平移未发生改变.由此可以看出绝对微分保证了平面上向量平移的两点性质,因此,为得到曲面上向量平行移动的概念可以用绝对微分替代普通微分.若DV=0,则称V沿曲线C是Levi-Civita意义下的平行向量场,或称向量场V是由初始向量v(t0)经Levi-Civita平行移动所得[7].特别地,在二维平面上,由于DV=dV,所以Levi-Civita平行移动归结为一般意义上的平移[8].

1.2 微分流形上向量的Levi-Civita平行移动的概念

在得到二维曲面上向量平行移动的概念后,考虑能否将其推广至高维欧氏空间.由n维拓扑流形定义可知,其上任意一点都有一邻域同胚于n维欧氏空间中的一个开集.因此,本节研究n维微分流形上向量的平行移动,微分流形就是附加了微分结构的拓扑流形[10].

根据Whitney定理,任意n维微分流形都可以看作充分高维欧氏空间的嵌入子流形[11],由于二维曲面是二维流形在三维欧氏空间的嵌入,所以在微分流形上同样可以采用向量投影的方法研究向量的平行移动.与上节类似,首先介绍一种新的微分法则,即协变导数.

设Y是微分流形M上沿曲线段γ: [a,b]→M的向量场,则Y沿γ的分布可表示为Y(t)=Yγ(t),而导向量场dY/dt一般不再与M相切,所以将其向切空间TpM做投影π,称π(dY/dt)为向量场Y沿曲线γ的协变导数,记为DY/dt.根据二维曲面上向量的Levi-Civita平行移动满足绝对微分为0的性质,同样令这里的协变导数DY/dt=0,得到微分流形上向量的Levi-Civita平行移动,称向量场Y沿曲线γ是平行向量场[12].

2 Levi-Civita联络

通过Levi-Civita平行移动,可以在微分流形上任意两点的切空间之间建立一个同构关系,即平移同构,而平移同构决定了微分流形上一个十分重要的几何概念,即联络[1].因此,可以通过联络从另一角度认识和理解Levi-Civita平行移动.

首先,对于上节所讨论的向量场Y沿曲线γ的协变导数DY/dt,若仅令微分流形M上任意一曲线γ满足γ(t0)=p,γ′(t0)=Xp,则称(DY/dt)p=DXpY为向量场Y在Q点沿Xp的方向导数,且满足以下性质:

(i) DfX+hYZ=fDXZ+hDYZ;

(ii) DX(fY+hZ)=(Xf)Y+fDXY+(Xh)Z+hDXZ.

其中X,Y,Z为M上任意可微向量场且f,h∈C1(M)[10].

上述定义仍是将微分流形作为欧氏空间的嵌入子流形考虑所得,接下来仅从微分流形本身出发,考虑其上向量场的微分.通过以上两个性质可以给出一个类似的结构定义,即线性联络.

定义1[10]设M是m维光滑流形,将其上全体光滑向量场所成之集记为X(M),并记M上光滑函数的集合为C∞(M).M上的线性联络是一个映射

且对于任意的X,Y,Z∈X(M)和任意的f,h∈C∞(M),满足:

由定义1知，联络的本质就是微分流形上向量场的一种与坐标选择无关的方向导数[11]，则前文中关于平行向量场的定义转化为：设X是沿曲线γ:[a,b]→M定义的向量场，若γ′(X)=0，则称X沿γ是平行的.下面探究联络的几何意义.对任意向量v∈Tγ(a)M，若存在沿γ的平行向量场X使得X(a)=v，X(b)=v则称向量v∈Tγ(a)M是向量v沿曲线γ作Levi-Civita平行移动得到的结果.由常微分方程组解的存在唯一性定理知，这样的向量场是唯一存在的[1].因此，有如下命题：

命题1[1]给定曲线γ:[a,b]→M,对任意的向量v∈Tγ(a)M,存在唯一沿γ的平行向量场X使得X(a)=v,从而唯一存在v∈Tγ(b)M作为v沿γ的平行移动的结果.

对于命题1中的曲线γ,若γ为浸入曲线则对其做微小分割即可[1].

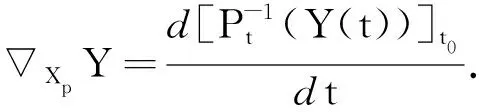
由此,得到联络的几何意义就是两个相邻的切空间借助沿两点连线的平行移动建立的同构关系[11],这里的同构关系也阐释了“联络”这一概念的含义.

一个微分流形上存在较多联络[1],为得到更好的性质,主要研究黎曼流形上一种特殊的联络,它仅依赖于黎曼度量g.由于方向导数作为联络是无挠的,且二维曲面的绝对微分D满足D(X·Y)=DX·Y+X·DY[10],即D与度量相容.将上述两个性质推广到黎曼流形上,得到黎曼流形M上Levi-Civita联络的定义.

定义2[10]设是光滑黎曼流形(M,g)上的一个线性联络,若对任意的X,Y,Z∈X(M),满足:

(ii)X〈Y,Z〉=〈XY,Z〉+〈Y,XZ〉,

3 Levi-Civita平行移动的性质

微分流形上向量场的Levi-Civita平行移动是欧氏几何中平面上向量平行移动的推广，两者在形式上截然不同，但在本质上有着相通之处.

首先,欧氏平面上的普通平移具有以下3个重要性质:

(i) 在欧氏平面上对任意向量v进行平移,其微分dv=0;

(ii) 向量在平移过程中保持长度和两向量夹角不变;

(iii) 欧氏平面上直线的切向量沿直线相互平行.

接下来,通过以上欧氏平移的基本性质,类比可以得到微分流形上的Levi-Civita平行移动也有相仿的性质:

引理1 微分流形上向量场的Levi-Civita平行移动具有如下性质:

(a) 若微分流形上向量场X沿曲线γ是平行向量场,则有γ′X=0;

(b) 在沿曲线的Levi-Civita平行移动下,向量长度与两向量夹角不发生改变;

(c) 微分流形中测地线的切向量场沿测地线本身是一个平行向量场[2].

证明首先,根据Levi-Civita平行移动的定义易得(a).

其次考虑(b).显然一般的联络不都具有这一性质，但是(b)在Levi-Civita联络上是成立的.设是黎曼流形M上的Levi-Civita联络,X和Y是沿曲线γ平行的向量场,即γ′X=γ′Y=0.由Levi-Civita联络的与度量相容性可知

因此,对任意两个沿曲线γ平行的向量,在Levi-Civita平行移动下其黎曼内积保持不变,所以向量长度与两向量夹角不发生改变.

下证(c).由于微分流形上的测地线是欧氏空间中“直线”概念的推广[13],所以考虑微分流形中测地线的切向量场沿测地线本身是否是一个平行向量场.

设γ:[a,b]→M是微分流形M上的测地线,则有

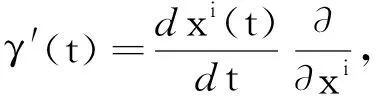
由Levi-Civita平行移动定义,证得(c).事实上,这一性质也给出了微分流形上测地线的另一定义:如果微分流形上一曲线的切向量场关于曲线本身是平行的,则该曲线为测地线[2].

4 总结

通过对文献的考证与研究,本文对于如何自然地引出向量Levi-Civita平行移动的概念及其性质作出了完善,循序渐进地将所讨论的空间由平直空间推广至二维曲面进而推广至微分流形,借助联络表明了研究Levi-Civita平行移动的重要意义,并通过与欧氏平移的基本性质类比,得到了Levi-Civita平行移动的基本性质.