一种充分下降的共轭梯度法及其收敛性

高前明

(南京财经大学 应用数学学院, 江苏 南京 210023)

0 引言

考虑无约束优化问题:

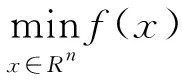
(1)

其中f:Rn→R是连续可微的目标函数,g(x)=f(x)是f(x)的梯度.在求解无约束优化问题(1)的众多经典算法中,共轭梯度法是一种备受研究者青睐的优化算法.由已知的初始点x0∈Rn,利用共轭梯度法可以得到如下迭代点列{xk}:

xk+1=xk+αkdk

(2)

其中αk>0为每一次迭代的搜索步长,由某种线搜索得到,其中有较为经典的弱Wolfe线搜索,

(3)

其中0<δ<σ<1.

dk为每一次迭代的搜索方向,其定义为

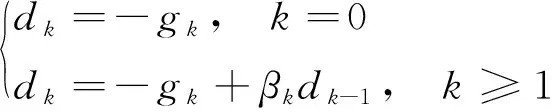
(4)

其中gk表示g(xk),βk是一个标量参数,用来调整每次迭代共轭梯度法的搜索方向.容易看出,βk的选取对共轭梯度法的全局收敛性和数值效果有较大影响.目前被广泛使用的βk的选取公式有如下4种:

分别被称为Fletcher-Reeves(FR)[1], Polak-Ribiere-Polyak(PRP)[2], Hestenes-Stiefel(HS)[3], Dai-Yuan(DY)[4],其中,‖·‖表示欧几里得范数.

众所周知,上述4种方法的收敛性质和数值效果有较大差异.通常FR方法和DY方法有良好的收敛性质,但数值实验效果不如PRP和HS方法;PRP和HS方法虽然数值效果好,但即使采用精确线搜索步长也无法保证它们的全局收敛性.因此,在这些经典算法的基础上,也有许多修正的共轭梯度法被相关研究者相继提出[5],并且有收敛性和数值效果都较为理想的方法.JIANG[9]等人提出了修正的DY(MDY)和修正的FR(MFR)共轭梯度法[9],它们均满足充分下降条件:

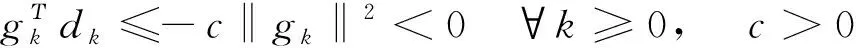
(5)

Tsegay[10]等人在JIANG和JIAN研究的基础上,提出一种新充分下降的共轭梯度法(SDCG),在多种线搜索下,它满足充分下降性式(5),并且在弱Wolfe线搜索下,证明了它的全局收敛性.文[10]中提出的算法βk的表达式为

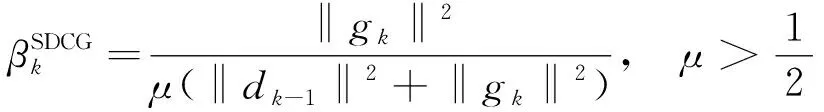
(6)

2006年，WEI[11]等人提出了一种修正的PRP(MYL)共轭梯度法,并满足充分下降性(5)式和全局收敛性.该算法中参数βk的表达式为

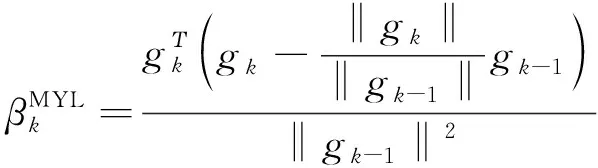
(7)

基于MYL和SDCG这两种修正的共轭梯度法,本文提出一种新的共轭梯度法,在多种线搜索下,它满足充分下降性,并且在弱Wolfe线搜索下,容易证明它的全局收敛性.

1 算法及其性质分析

1.1 算法

通过修正βk,提出一种新的充分下降的共轭梯法,其参数βk表达式如下:

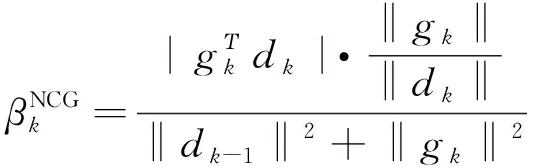
(8)

为了方便,NCG用来表示本文提出的新型共轭梯度法,并基于弱Wolfe线搜索,给出如下算法步骤:

算法1 初始化给定ε>0,δ∈(0,1),σ∈(δ,1),x0∈Rn.令d0=g0,k=0.

步骤1: 若‖gk‖≤ε,则停止;否则,进入步骤2；

步骤2: 通过使用弱Wolfe线搜索确定步长αk；

步骤3: 更新迭代xk+1:=xk+αkdk；

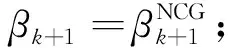
步骤5: 令k:=k+1,并返回到步骤1.

1.2 算法的充分下降性

通过下面引理,可以得出新方法在多种线搜索下的充分下降性.

引理1 在某种线搜索下,考虑共轭梯度法中的βk为表达式(8),则充分下降条件式(5)成立.

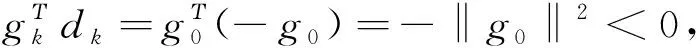
对于任意两个向量μ和ν,有

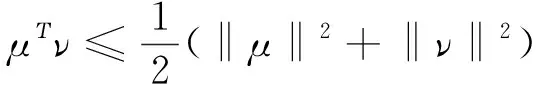
(9)

结合式(8),可得

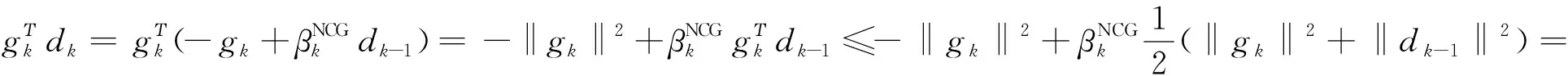
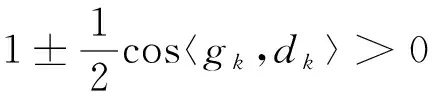
1.3 算法收敛性

为保证算法的全局收敛性,给出如下假设：

(H1) 水平集Λ={x∈Rn|f(x)≤f(x0)};

(H2) 目标函数f(x)在水平集Λ上是连续可微有下界的,并且它在梯度水平集Λ上是Lipschitz连续的.即存在一个常数L>0,使得,

‖g(x)-g(y)‖≤L‖x-y‖,∀x,y∈Λ

(10)

成立.

引理2(Zoutendijk条件)[12]假设(H1)和(H2)成立,dk为共轭梯度法的下降方向,并且步长αk满足弱Wolfe条件(3),则有

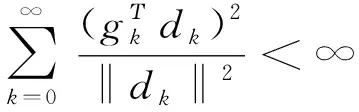
(11)

证明由式(3)中的第二个式子和Lipschitz条件,得

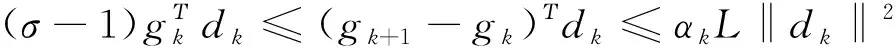
(12)

所以

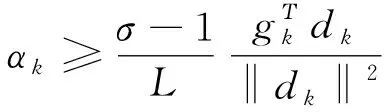
(13)

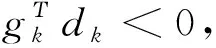
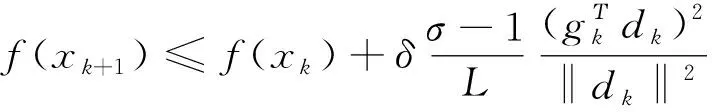
(14)

将上式不等号两边分别对k求级数,并利用{f(xk)}单调不增有下界的性质,得

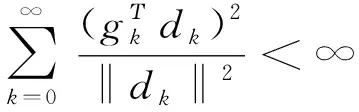
(15)

证毕.

由引理2,即可得到下面的定理.

定理1 在假设(H1)和(H2)成立的条件下,点列{xk}由算法1产生，则

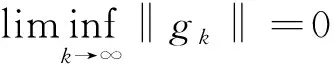
(16)

证明假设式(16)不成立,则存在一个常数ρ>0,使得‖gk‖2≥ρ,∀k≥0.由式(4)和式(8),有

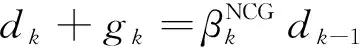
(17)

将式(17)两边同时平方,可得

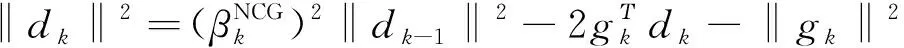
(18)

从而,由式(5)和式(8)可得

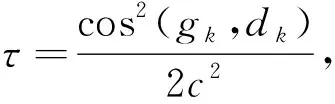
因此

从而有

由引理2,定理1得证,说明此方法具有全局收敛性.

2 数值实验

本节通过数值实验来说明NCG算法的有效性.实验测试在PC机上完成,PC机配置:1.80GHzCPU,8GB内存, windows10家庭中文版操作系统.编程软件为MatlabR2018a.

测试对象:函数Example和来自Neculai[13]的函数(见表1),Example的表达式如下:

x1=(x11,x12,…,x1n)=(3,3,…,3).

测试参数:δ=0.4,σ=0.6,ε=10-6.

终止条件:‖gk‖≤ε=10-6或迭代次数I>1000.

分别采用本文NCG算法和SDCG算法[10]两种算法求解上述测试问题.测试结果见表1.

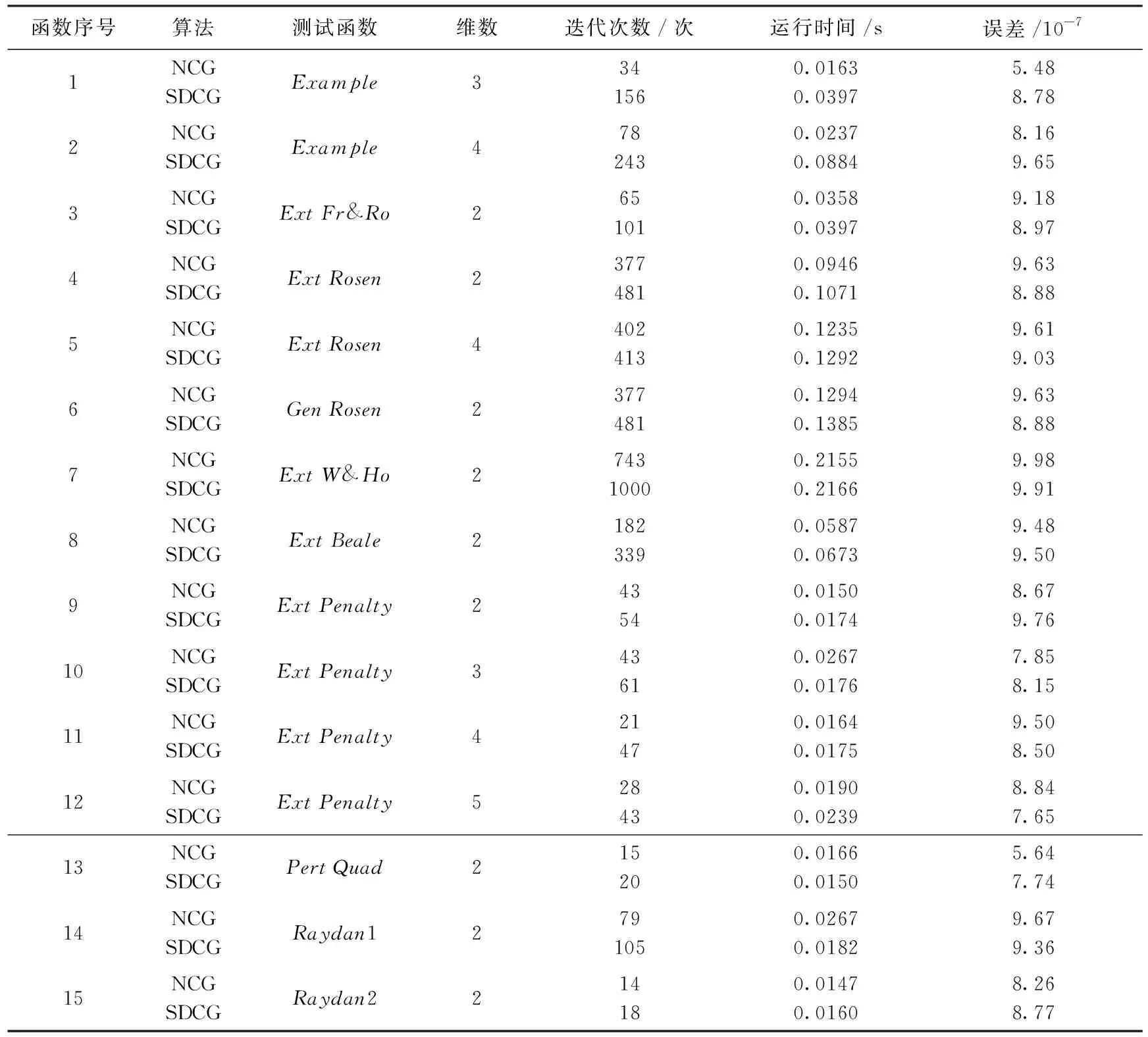
表1 本文NCG算法和SDCG算法的测试结果

在迭代次数和运行时间两个方面,NCG算法的数值实验效果都要优于SDCG算法，实验结果如图1和图2所示.此外,在充分下降性的理论分析方面,SDCG算法的下降性取决于参数μ的取值范围,而本文所提的NCG算法,不依赖于其他参数的取值范围,即具有自动下降的性质.综上,NCG算法是一种有效的新型共轭梯度法.

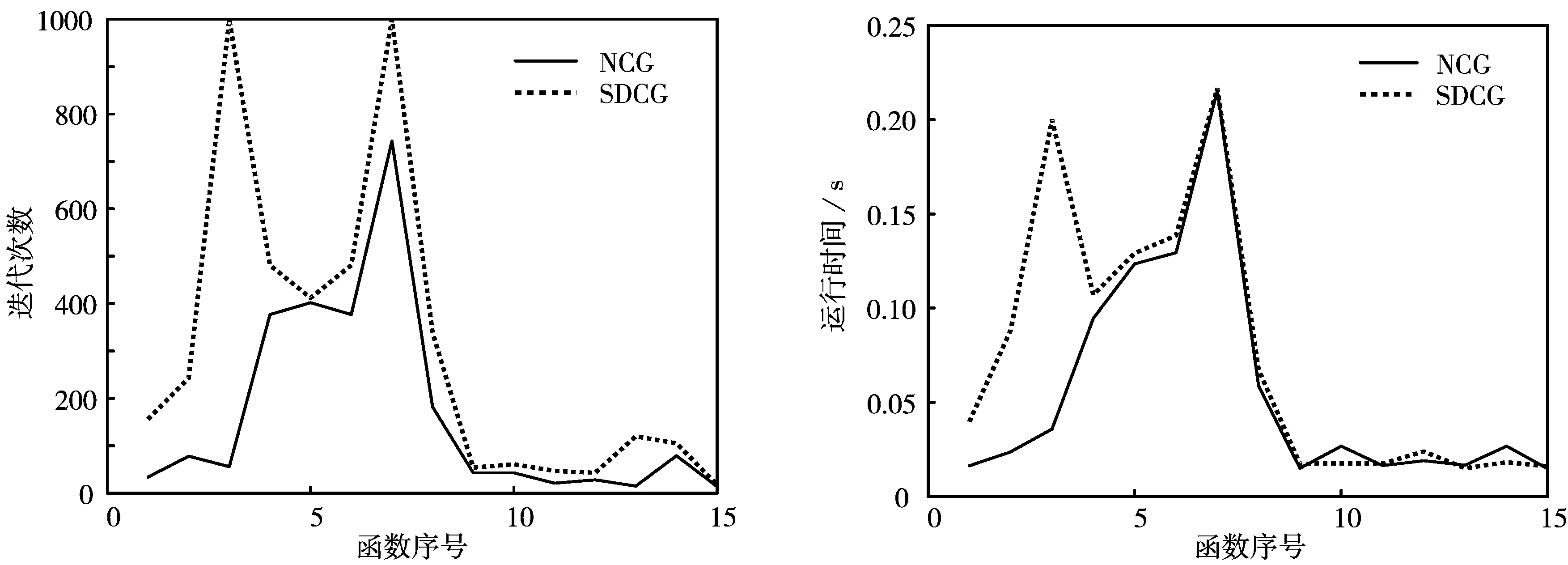
图1 算法的迭代次数 图2 算法的运行时间