数学解题后反思对学生思维品质的培养

范启樟

摘 要：随着新课改的不断深入，使得传统教育模式发生了较大的改变，更加强调学生的主体性地位。对于中学数学而言，则强调学生学习方式的转变，教师应引导学生进行学习反思，既反思成功之处，也反思自己的不足，对现有的学习方法进行调整或完善，从而达到培养与发展学生思维品质的目的，进而为学生的终身发展服务。基于此，本文主要从中学数学解题反思这一角度探讨培养学生思维品质的策略，以供参考。

关键词：中学数学;解题反思;思维品质;培养策略

引言：在中学数学教学中，培养学生数学能力的核心便是思维能力的培养，而这就需要教师重视学生思维品质的培养，这样才能够有效提高学生的思维能力。如何实现培养学生思维品质的目的，不妨从数学解题方面着手，因为解题能力是数学能力的重要体现。在数学解题过程中，需要经过审题、分析、求解、回顾等几个过程，其中回顾也就是再思考尤其重要，其可以说是解题的归宿，如果只是解题，而不在解题后思考研究，那么解再多的题也无法实现能力的提高，只能是被“题海”灌的晕头转向。因此，在中学数学教学中，教师可通过解题后的反思教学来实现培养学生思维品质的目的，从而提高学生思维能力，进而为学生的终身发展服务。

一、中学数学教学中解题后反思的重要性及作用

（一）解题后反思的重要性

解题是中学数学学习中常遇到的项目，数学解题的目的是帮助学生将所学的知识运用至实践中，从而提高学生的数学能力。随着新课改的全方位推进，数学教育也更强调以学生发展为核心，不断提升学生数学基础知识及数学能力的同时，发展学生的创新精神和实践能力，使学生能够形成良好的数学思维，提高学生的数学素养。而这一教学目的的实现，需要教师重视引导学生在解题之后进行必要的反思，让学生的思维保持高度的活跃性。在以往的数学教学模式中，由于往往是“灌输式”教学，使得学生学习兴趣不高，且在课堂教学中大多数是教师让学生解答一些结构良好的问题，学生主动提出问题的现象较少，以至于教学效果并不佳。另外，许多教师存在重视解题技巧的训练，但忽视普适性思考方法的培养，方法论层次的内容滲透不够深入，以至于机械化的模仿缺少独立思考的机会，加之多关注基本概念，缺乏数学思想，这些都不利于学生数学素养的提高。如何解决这样的困局，需要学生学会反思，在提前预习时反思，在课堂学习中反思，在复习过程中反思。尤其是要在解题后反思，反思课本中出现的概念，深刻理解其内涵及外延;反思每个数学问题的思想方法和逻辑，领悟数学本质和体验数学中的理性精神;反思解题技巧和涉及的数学知识，学会识别问题的关键。只有从各个角度引导学生进行反思，强调过程的思想性，让学生经历实质性的数学思维过程，这样才能够达到事半功倍的效果，才能够有效发展学生的创新思维。

（二）解题后反思的作用

解题后反思实际上就是对问题解答进行一次“再认识”的过程，对解题活动进行深层次的思考。首先，引导学生解题后反思，能够改善学生的思维习惯，并且提高学生的解题能力。在数学解题过程中，学生难免会出现这样或那样的错误，可能是因为思维逻辑、策略方法导致，也可能是因为自身的知识与能力导致，而通过反思错误，让学生弄清楚错误的根源，明白错误的原因，并对容易出错的地方进行总结，从而提出正确的解题思路和方法，可见反思是最有效的纠错手段。其次，引导学生解题后反思，能够大大提升学生的学习效率。当前在中学数学教学中，许多教师不可避免会采用“题海”战术，主要是想借助这一方法来让学生懂得举一反三，并提高学生的解题能力。然而实际效果并不佳，大量的数学问题解题让学生又苦又累，容易产生疲倦，且做得多，思考的少，并不能真正的把握问题之间的内在联系，只会逐渐丧失学习的兴趣。所以需要教师及时引导学生解题后进行反思，通过反思每个数学问题的思想方法和逻辑，探索问题的本质规律，这样才能够达到举一反三、提高学习效率的效果。

二、利用解题后反思培养学生思维品质的策略

（一）利用易错题引导学生反思总结

在中学数学学习中，学生对一道题做过很多遍，即便教师讲解过许多次，但是仍然一错再错，这样的题目便是易错题。导致易错题出现的原因有许多，可能是学生审题不清，可能是学生不懂得运用数学公式等。实际上这些错题的纠正是培养学生思维品质的良好素材，通过利用易错题引导学生反思总结，清楚自己错误的原因，并采取对应的纠正措施。这样不仅能够让学生熟练且正确的运用数学知识与概念，而且学生的反思错误过程，也是思维创造性的过程，如此便能够达到培养学生思维品质的目的。

例如：两个互为相反数的数中，是否必有一个正数，一个负数？

错解：是

正解：不一定

分析：零的相反数就是其本身，因此两个互为相反数的数，并不一定是一个正数和一个负数。导致学生解这道题出现错误的原因便是忽略了“零的相反数是零本身”这一概念，教师可以利用这样典型的错题引导学生反思，引导学生反思问题中涉及的数学概念，让学生自己分析出错的原因，数学中每个概念的定义都是严密的，一定要有一个严谨的学风，通过对这类型的误解进行再思考，可以加深学生对数学概念的理解，从而避免错误再产生，进而培养学生思维的严密性和批评性。

（二）引导学生反思解题技巧及涉及的数学知识

引导学生反思解题技巧及涉及的数学知识，即通过多个解题角度培养学生创造性思维，引导学生从多个角度去分析问题的解法，掌握识别问题的关键，从而一步到位地解决问题。在中学数学学习中，由于受到传统教育模式的影响，学生主动提出问题的现象较少，以至于学生数学思维层次并不能有效提高。针对这样的问题，教师应善于引导学生提出问题，并对自己提出的问题进行思考，同时要关注解题过程，而不是看重结果，应针对一个数学问，或一个题设，从多个角度思考，打破单一的思维模式，寻找多个突破点，从而有效发展学生的创新思维。比如，对同一个题目，引导学生从不同的角度分析研究，探索多种解题思路，并思考其中所涉及的数学知识，可以有效培养学生思维的广阔性和创造性;或者通过“多题一解”的方式，引导学生反思，找出数学知识之间的联系，以此获得最基本的解题方法，也有利于培养学生的思维概括性;另外，也可以利用“一题多变”的反思来培养学生思维的灵活性，在数学学习过程中，数学问题实际上是形式多样的，学生如何灵活应对多变的问题，就需要教师借此机会对问题进行延伸，引导学生将一道题演变成一类题，使学生能够体会一类题，这样学会一道题便学会一串题，从而有效提高学生解决问题的能力，并且可以培养学生思维的深刻性和创造性。

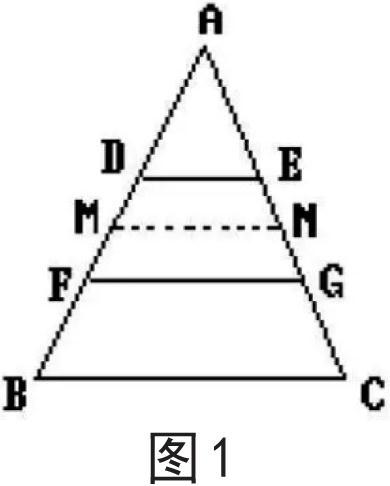
例如：△ABC中，D、F在AB上，AD=BF，过D作DE∥BC，交AC于E，过F作FG∥BC交AC于点G.求证：BC=DE+FG.

分析：这道题主要是证明一条线等于另外两条线段的和，有多种解题方法，常用的方法便是将线段的位置进行平移。为了能够培养学生思维的广阔性和创造性，教师可引导学生对这一问题从不同角度进行研究，探求多个解题思路，如通过延长较短线段与较长线段相等的方式，即延长FG到H，使FH等于BC，联结CH，然后证明GH=DE即可;或者可以利用梯形或三角形的中位线定理，猜想通过梯形DFGE的中位线沟通两者之间的关系，如图所示，作梯形DFGE的中位线MN，则MN=（DE+FG）/2，又AD=FB，由平行截割定理得MN也是△ABC的中位线，所以MN=BC/2，这样便可得知BC=DE+FG。

（三）引导学生反思问题的思想方法和逻辑

在数学学习中，数学思想方法是数学解题的灵魂，如何领悟数学本质，并体验数学中理性精神，关键在于数学思想方法，而不是只关注细枝末节，只有在解题后引导学生反思每一个数学问题的思想方法和逻辑，结合不同的数学内容引导学生联系并启发，让学生能够经历知识概况的过程，在数学形式下进行思考和推理，这样才能够提高学生数学知识的思维能力，才能够达到举一反三的效果。为此，教师应注重引导学生反思自己解题的过程，在自我剖析清楚原因的基础上，对解题的思想方法和逻辑进行反思，包括解题策略和思路选择运用的成与败，分析它们的成功之处，分析它们的特点、适用条件，概括出思维规律，促使自己思维方式的转变。数学解题并不只是简单地将知识进行联结，而且也是数学思想和解题方法反复推进的过程，所以数学解题除了要让学生直接参与解题外，也要参与解题的思维活动，在解题后反思问题的思想方法和逻辑，依据问题的特征进行多个角度的联系，看解答过程是否有错，而不是简单的检查结果的错与对，从而积累解题经验，形成良好的思想习惯。

分析：学生在解这道题时，往往会滥用“加法结合律”，将结合成-（），最后导致计算结果出现错误。针对这样的问题，教师引导学生对问题的解题过程进行分析和反思，除了要检查答案的对错以外，更重要的是引导学生对这一问题的解题过程进行检查，看解答过程是否有错，错误的原因在哪，明白在哪个环节出现了错误，然后看能否有别的解答方法。之后学生通过反思可以通过运用加法运算律来解答这道题，这一方法能够将解答过程简化，可以有效避免错误，提高了学生数学知识的思维能力。

（四）引导学生反思解题结果

在解题后，引导学生对解题结果进行反思，实际上就是引导学生对验证过程进行再次的推算和推理，一方面可以有效保证答案准确无误，另一方面也能够培养学生良好的解题习惯，进而提高学生审题能力和良好的思维品质。在数学解题过程中，由于数学问题具有严密性和逻辑性，容不得半点马虎，有时可能会因为一时疏忽或一念之差就會导致错解。因此需要教师引导学生反思解题结果，通过对解题结果进行反思，考查学生审题的严密性和规范性，从而培养学生形成良好的解题思维习惯和思维的严密性。

结束语

总之，在中学数学教学过程中，教师要重视学生思维品质的培养，这是提高学生数学能力的关键，通过培养学生的思维品质，使学生能够形成良好的思维习惯，才能从根本上激发学生对数学学习产生兴趣，让原本枯燥乏味的数学学习变得兴趣盎然，从而让思维品质成为学生数学学习的推动力，进而为学生的全面发展而服务。

参考文献

[1]曾平.浅谈初中数学解题教学中逆向思维的应用[J].科技经济导刊，2020，28（18）：175.

[2]杨超、王新民.教学方式对初中生数学解题思维监控能力影响[J].内江师范学院学报，2019，34（06）：18-23.

[3]文萍.再谈解题过程中的数学直觉[J].玉溪师范学院学报，2019，35（03）：21-26.

[4]陈媚娜.提高中学生数学解题能力方法研究[J].才智，2019（12）：2.

此文系南平市中小学骨干教师培养对象培训课题课题研究项目，课题名称《初中生数学考试后反思意识的培养之探究》课题成果，课题编号：zxsxgg2020028