挖掘习题内涵 渗透数学文化

梁玲智

[摘  要] 引导学生探究“杨辉三角”，发现数字之间的规律，感受“杨辉三角”的美，了解“杨辉三角”在数学中的应用。教师应该采取有效的教学策略，设计与习题相关的问题，帮助学生在问题解决中感受数学文化，在规律探究中欣赏数学文化。

[关键词] 习题教学;数学文化;杨辉三角

一、教学背景

数学是人类文化的重要组成部分，数学文化是数学教学不可分割的一部分。人教版数学教材里编排了丰富的数学文化知识，除了在“你知道吗”栏目集中呈现外，练习题里也有不少和数学文化有关的题目。如六年级上册第八单元《数与形》的练习里，就有一道关于“杨辉三角”的题目。

我国宋代数学家杨辉在公元1261年撰写了《详解九章算法》，杨辉在这本著作中画了一个由数构成的三角形图，我们把它称为“杨辉三角”。你能发现下面（图1）与“杨辉三角”图对应的数字三角形表中各数之间的关系吗？你能按照发现的规律把这个三角形表继续写下去吗？试试看。

“杨辉三角”是我国南宋数学家杨辉的一个重要数学研究成果，是二项式系数在三角形中的一种几何排列。它把二项式系数排成三角形的形式，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。

在数学教学中渗透数学文化，能“帮助学生了解数学在人类文明发展中的作用，激发数学学习兴趣，感受数学家治学的严谨，欣赏数学的优美”。如果仅按照题目的要求，让学生发现数之间的关系并按照发现的规律继续写下去，学生并不能体会“杨辉三角”的伟大，也不能理解其在数学史上为什么会具有如此重要的地位。所以，教师应该采取有效的教学策略，设计与习题相关的问题，帮助学生在问题解决中感受数学文化，在规律探究中欣赏数学文化。

二、教学实践

1. 发现规律

逐层出示图2。

师：这是一张三角形的表。把数字排成三角形形状，是我国南宋末年数学家杨辉的创举。数学史上把这样的三角形表称为“杨辉三角”（板书）。大家观察一下，“杨辉三角”中数字的排列有什么规律？

生答（略）。

师：请大家按照发现的规律，在空的圆圈里填上适当的数。

学生操作，教师根据学生的汇报把三角形表填完整。（图略）

【设计意图】 观察“杨辉三角”，发现数字排列的规律，是欣赏数学文化的开始。相比让学生直接观察完整的前6行数据，或者由教师直接介绍规律，本教学环节的探究活动使学生从被动接受者转变为主动发现者，更能激发学生的学习积极性。从而使学生发现奇妙的数学规律，亲近数学文化，悦纳数学文化。

2. 感受“杨辉三角”的美

师：有的同学在嘀咕了，这么简单的数字排列，居然被称为创举？同学们，虽然“杨辉三角”的数字和排列规律都非常简单，但在数学学习中是非常有用的。虽然相关的一些知识要到初中才学习，但“杨辉三角”中一些奇妙的规律，我们小学生也能去探究。

（1）和2的幂的关系

师：请大家横着把前5行每一行数分别相加。

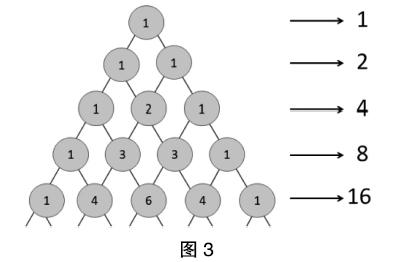
学生操作，反馈，在PPT上呈现答案（图3）。

师：有什么发现？

生1：都是两倍的关系。

生2：后面的数都是前面数的两倍。

师：能把这些数写成2的几次方的形式吗？

生：2等于21，4等于22，8等于23，16等于24。

师：猜一猜，下一行数的和是几？

生1：32。16×2=32。

生2：32也就是2的5次方。

师：让我们验证一下。（学生验证）正确！在数学上，2的0次方就是1。这里每一行的数的和，都可以写成2的几次方形式。实际上，“杨辉三角”最初就是用来解决两个数或字母相加和的几次方的问题的。

（2）和11的幂的关系

师：你们能口算11的平方吗？

学生马上回答：121。

师：11的3次方呢？

学生迟疑，有的口算，有的列竖式计算。过一会儿，报出答案：1331。

教师微笑着指指“杨辉三角”的第4行，学生一片哗然。

师：11的4次方呢？

生：14641！

师：你怎么算得这么快？

生：杨辉三角的第5行就是这个数。

师：真会思考。我们用计算器验证一下。（验证）正确。

师：11的5次方呢？

生：151051！

教师用计算器计算14641乘11，得到161051。学生发出“啊”的声音。

师：怎么回事？

生：我知道了。这里的6+4等于10，其实是要向前一位进1的。然后4加6等于10，加上1是11，写1进1;5加1等于6，所以是161051。

教师在PPT上演示，得出杨辉三角中的数字是正确的，但由于要满十进一，所以最后写出来的数发生了变化。

（3）和三角形数、四面体数的关系

教师演示（图4-1）：斜着看，有什么发现？

生：第一列都是1，第二列一个一个大起来，第三列是加2，加3，加4，第四列是加3，加6，加10……都是有规律的。

師：右边（或左边）第二列都是自然数序列，右边（或左边）第三列都是三角形数序列（出示图4-2）。请大家翻到书本第109页，看到练习二十二第2题。

师：接下来的一个三角形数是15，请同学们用图表示出15。（学生画，略）

师：下两个三角形数分别是什么？请画图表示。

学生操作（略）。

师：右边（或左边）第四列都是四面体数，我们欣赏一下（图4-3）。

3. 杨辉三角的应用

师：“杨辉三角”利用数与形的巧妙统一，在解决一些数学问题时可以起到很好的作用。我们来看下面的例子：

从A到B之间有很多交叉路口。如果只能向右或向下走，那么从A到B一共有几种不同的走法？（如图5-1）

学生尝试操作，会发现比较困难。

教师提示：把图顺时针旋转45°，转化为类似“杨辉三角”的图形，把每一个交叉点上的走法标出来，用“杨辉三角”的知识来解决（图5-2）。

小结：杨辉三角中的奥秘还有很多，等待同学们进一步去发现。

4. 杨辉及“杨辉三角”在数学史上的地位

PPT出示，略。

【设计意图】在习题教学中渗透数学文化，要根据学生的学习基础展开，不过分拔高，不偏离教学目标。“杨辉三角”，本意是解决二项式系数问题的，但其中还蕴藏着很多奇妙的规律。除文中呈现的之外，还有与斐波那契数列之间的联系，与组合数之间的联系等。这些知识，有些超出了六年级学生的认知范围，有些和本单元《数与形》的教学目标不相符，所以没在教学中呈现。

三、教学体会

“杨辉三角”是中国古代数学史上光辉灿烂的一页。引领学生探寻“杨辉三角”的奥秘，不仅能加深学生对“杨辉三角”的认识，还可以让学生更好地感受数与形之间的相互作用，受到数学文化的熏陶。如果教师能充分认识数学习题里蕴含的数学文化价值，以问题引领，让学生经历探究数学规律的过程，就能帮助学生更好地感受数学文化，欣赏数学文化，体会数学的思想、精神和价值。