多跨高墩变截面梁桥的动力学特性研究
2021-09-27周文鑫张建东
周文鑫,周 叮,张建东,刘 朵
(1.南京工业大学 土木工程学院,南京 211816;2.苏交科集团股份有限公司,南京 211112)
多跨高墩桥梁以其跨越能力大、整体性能好等特点成为我国西部地区广泛修建的桥型之一,其模型如图1所示。高墩柱桥梁一般采用双肢薄壁空心墩,空心截面抗弯刚度较大[1],双肢墩的横向刚度较小,可使桥墩柔性大幅度提高[2]。箱形截面具有稳定性好和刚度大等特点[3],成为多跨高墩桥梁截面形式的首选。变截面梁可改善结构自重分布,外形美观,在桥梁结构中被广泛应用[4],其梁高沿跨径一般为直线、圆弧形和二次抛物线变化等,其中二次抛物线应用最多。
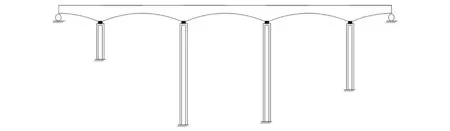
图1 多跨高墩桥梁模型Fig.1 The model of multi-span high-pier bridge
有关多跨高墩桥梁的动力学特性研究比较复杂。首先,主梁截面面积和惯性矩沿跨径方向不断变化,其振动方程是变系数的微分方程,难以得到解析解,半解析法成为解决此类问题的近似途径。Lee等[5]用传递矩阵法和Frobeniu法得到了Euler-Bernoulli梁自由振动的幂级数解。Firouz-Abadi等[6]通过WKB展开级数法求解轴向变截面Euler-Bernoulli梁自由振动的控制方程,得到了自振频率的近似解。Duan等[7]对离散奇异卷积方法进行改进,提高了多步变截面梁自由振动近似解的精度。崔灿等[8-9]将一变截面梁划分为若干个子梁,由各子梁段间力和位移的连续条件,研究了变截面梁动力特性。闫维明等[10]基于Euler-Bernoulli梁理论改进了直接模态摄动方法,形成了完全弹性支承情况下变截面梁振动方程的半解析法。半解析法需找出函数的表达式,但不是每个问题都可以找到函数表达式。其次,对于多跨桥梁,文献[11]将主梁沿桥墩分成若干段,分别求得各段主梁自由振动精确解后,利用桥墩顶部位移变形协调导出频率方程,振型函数分段表示,当桥墩个数较多时,分析较为复杂。
本文假定各中跨梁长是相等的,边跨梁长为中跨梁长的一半,各跨梁高均按相同的二次抛物线变化,基于等效原则和能量法求解梁的等效截面面积和惯性矩。将桥墩简化为弹性支承、推导支承刚度与桥墩及支座的参数关系。最后,将支承反力看作是梁上的未知外力,求得了主梁竖向振动与横向振动时固有频率及振型解析解。
1 分析模型
本文将桥墩简化为弹性支承,将变截面主梁等效成等截面的Euler-Bernoulli梁,建立了一个带有多个弹性支承的多跨直梁分析模型,如图2所示。

图2 多跨弹性支承直梁力学模型Fig.2 Mechanical model of straight beam with multi-span elastic supports
2 主梁等效计算
2.1 等效截面面积
对于高度按二次抛物线变化的梁,如图3所示。梁截面高度为
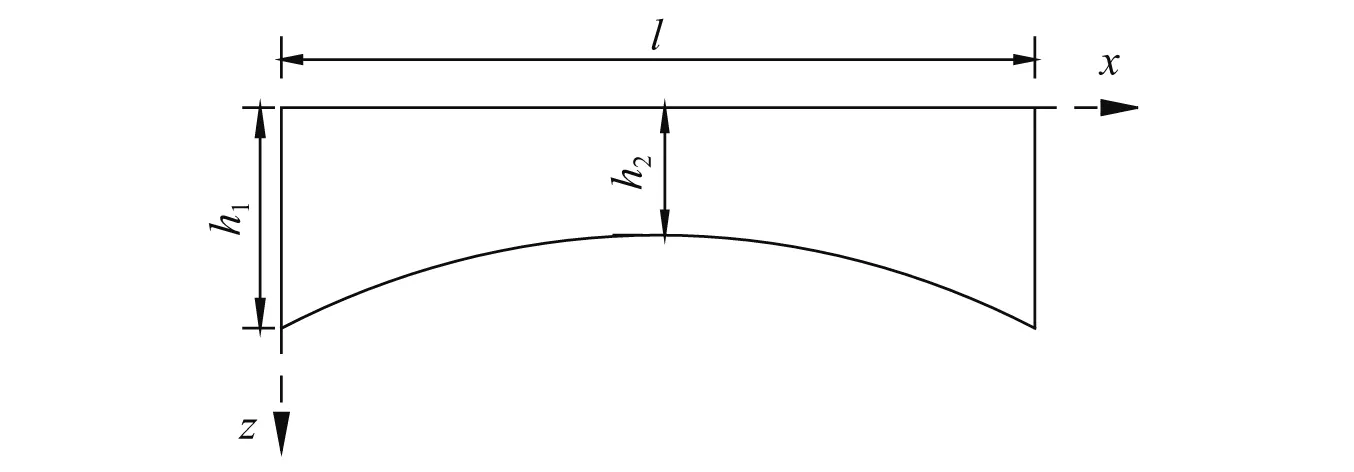
图3 变截面梁Fig.3 Variable cross-section beam
(1)
式中:h1为根部梁高;h2为跨中梁高;l为梁长。
梁截面示意图,如图4所示。梁截面面积为
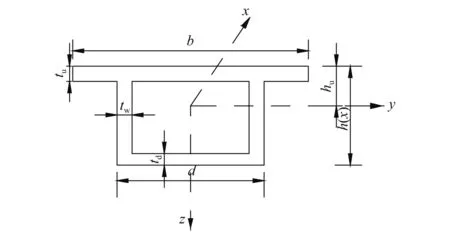
图4 梁截面示意图Fig.4 Beam section diagram
A(x)=btu+dtd+2tw[h(x)-tu-td]
(2)
式中:b为箱形截面上翼板宽度;d为下翼板宽度;tu为上翼板厚度;tw为腹板厚度;td为下翼板厚度;h(x)为截面高度,其值由式(1)可得。
则等效截面面积A为
(3)
2.2 等效惯性矩
如图4所示,当梁竖向振动时,y轴为截面中性轴,截面对y轴的惯性矩为
Iy(x)=btu(hu-tu/2)2+dtd[h(x)-hu-td/2]2+
2tw[h(x)-tu-td][h(x)/2-hu+(tu-td)/2]2
(4)
式中,hu为形心距,其表达式为
(5)
式中,h(x)由式(1)可得。
当梁横向振动时,z轴为截面中性轴,截面对z轴的惯性矩为
(6)
式中,h(x)由式(1)可得。
梁截面等效示意图如图5所示,变截面梁任意截面惯性矩为Ix,其等效梁任意截面惯性矩为I。
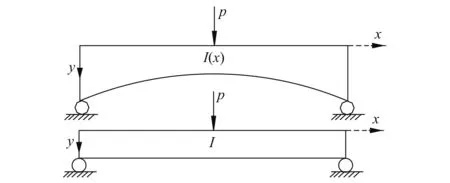
图5 等效示意图Fig.5 Equivalent diagram
两梁跨中分别作用一集中力,由弯曲应变能相等原理建立下列等式
(7)
式中,y为梁的挠度曲线方程,可表示为
(8)
式中:αi为参数;fi(x)为满足边界条件的已知函数,可参照表1所列4种不同边界梁选取。

表1 不同边界梁对应的挠度曲线方程Tab.1 Deflection curve equation of beams with different boundary conditions
若挠度曲线方程只包含一个参数,将其代入式(7)化简可得梁的等效惯性矩I。
若挠度曲线方程包含两个及以上参数,由两梁的弯曲应变能会出现误差Q,即
(9)
为使误差最小,令
(10)
可得以参数a1,a2,…,an为未知数的齐次方程组,若方程组有非零解,其系数行列式应等于零,由行列式搜根法可得梁的等效惯性矩I。
3 桥墩支座集成刚度
3.1 桥墩截面面积及惯性矩
工程中高墩柱通常采用空心截面,其纵桥向一般为变截面,横桥向为等截面,计算模型如图6所示。
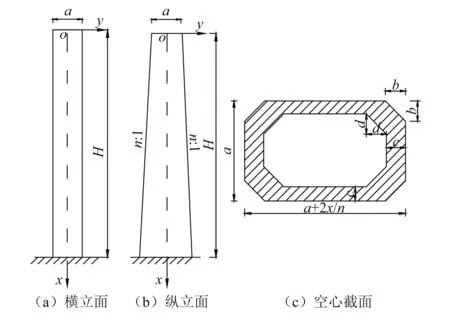
图6 桥墩计算模型Fig.6 Calculation mode of piers
桥墩截面面积为
(11)
式中:n为纵桥向放坡系数;a,b,c,d为空心截面各边长尺寸,如图6(c)所示。
桥墩截面等效面积Se为
(12)
式中,H为桥墩高度。
将式(11)代入式(12),得
(13)
桥墩截面惯性矩为
(14)
桥墩截面等效惯性矩Ie为
(15)
利用柯特斯公式计算截面惯性矩,其定义为
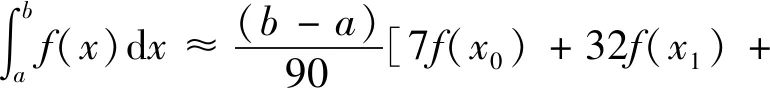
(16)
利用式(16)的性质,将式(14)代入式(15),得
(17)
3.2 竖向集成刚度
桥墩竖向刚度为
(18)
式中:Ee为桥墩弹性模量;Se为桥墩截面等效面积;H为桥墩高度。
支座竖向刚度为
(19)
式中:Ec为支座弹性模量;Sc为支座截面面积;D为支座厚度。
单肢桥墩与支座的竖向集成刚度为
(20)
式中,K桥墩(竖),K支座(竖)由式(18)、式(19)可得。
双肢墩竖向刚度计算模型,如图7所示。每单肢墩与纵梁通过支座连接,纵梁上作用一竖向力,将支座看成固定铰,根据两单肢墩压缩变形量相等,可取单肢墩计算,单肢墩受竖向力F/2,由单肢墩的计算模式知,双肢桥墩与支座的竖向集成刚度为
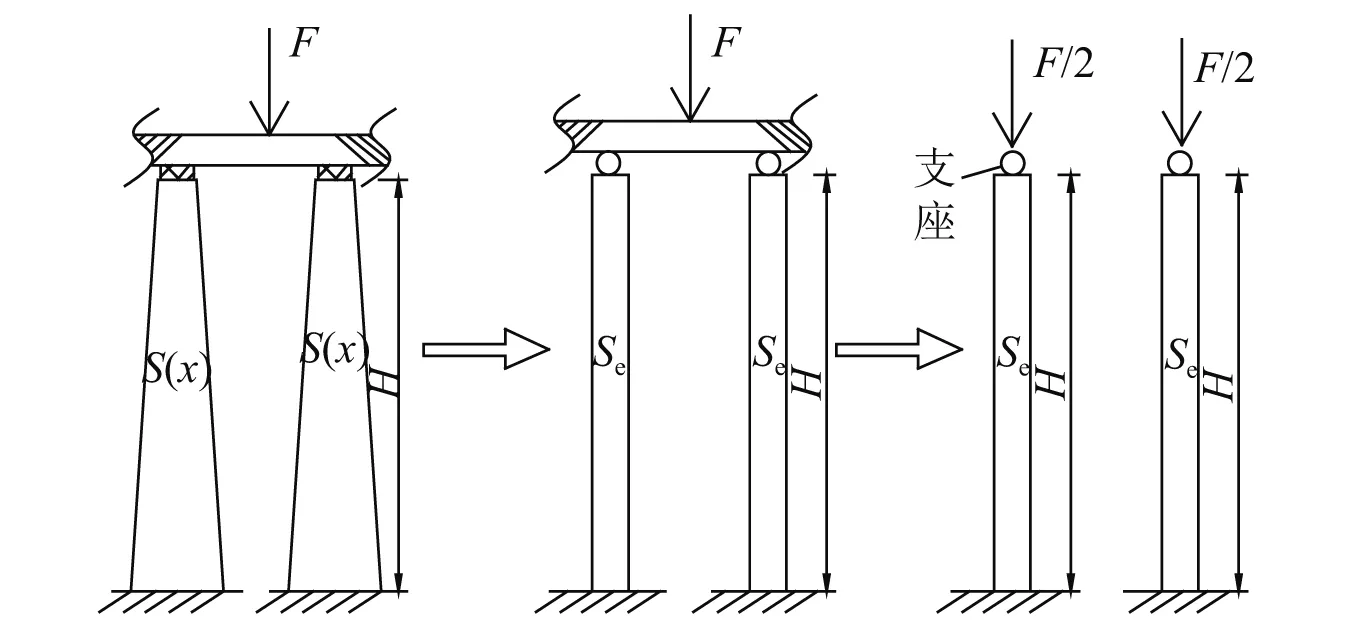
图7 双肢墩竖向刚度计算模型Fig.7 Calculation model of vertical stiffness of two-limbed pier
(21)
3.3 横向集成刚度
桥墩横向刚度为
(22)
式中:Ee为桥墩弹性模量;Ie为桥墩截面等效惯性矩;H为桥墩高度。
支座横向刚度为
(23)
式中:Gc为支座剪切模量;Sc为支座截面面积;D为支座厚度。
单肢桥墩与支座的横向集成刚度为
(24)
式中,K桥墩(横),K支座(横)由式(22)、式(23)可得。
为双肢墩横向刚度计算模型,如图8所示。不计纵梁对桥墩顶部转角约束,根据双肢墩变形为反对称,可取单肢墩计算,单肢墩受水平力F/2,由单肢墩的计算模式知,双肢桥墩与支座的横向集成刚度为
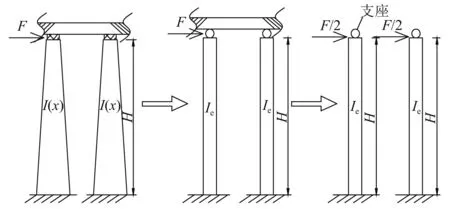
图8 双肢墩横向刚度计算模型Fig.8 Calculation model of transverse stiffness of two-limbed pier
(25)
4 频率及振型
不考虑阻尼C的影响,在任意外力作用下,等截面直梁受迫振动微分方程[12]为
(26)
式中:y(x,t)为梁的竖向(横向)位移;x为沿梁轴线的坐标;t为时间;E为弹性模量;I为梁截面等效惯性矩;ρ为梁的体密度;A为梁截面等效面积;p(x,t)为作用于梁上的外力。
当弹性支承直梁作自由振动时,支承反力随时间的变化频率等于梁的自振频率。此时,将支承反力看作是梁上的未知外力,则有
y(x,t)=Y(x)eiωt,p(x,t)=P(x)eiωt
(27)
假设共有N个弹性支承,则支承反力可表示为
(28)
式中:Pi(i=1,2,…,N)为各弹性支承对梁的作用反力;xi(i=1,2,…,N)为各弹性支承的坐标值;δ(x-xi)为Dirac Delta函数,其定义为
(29)
令ξ=x/l,利用式(29)的性质,将式(28)改写为
(30)
将式(27)、式(30)代入式(26),得
(31)
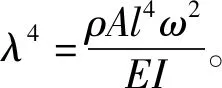
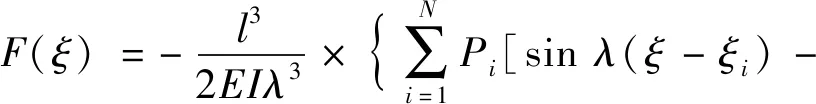
(32)
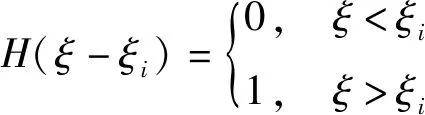
对于第i个弹性支承,支承点处位移、转角和弯矩均是连续的,而剪力不连续,剪力跳跃值即为支承反力值,支承反力与梁位移间的线性关系为
Pi=-KiY(xi)=-KiY(ξi),i=1,2,…,N
(33)
式中,Ki为第i个弹性支承(桥墩)的刚度。当梁竖向振动时,对于单肢桥墩,其值由式(20)可得,对于双肢桥墩,其值由式(21)可得;当梁横向振动时,对于单肢桥墩,其值由式(24)可得,对于双肢桥墩,其值由式(25)可得。
将位移函数Y(ξ)代入式(33),可得关于Pi的N阶齐次线性代数方程组
(34)
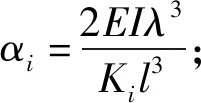
对于简支-简支边界条件
[sinλ(ξi-ξn)-sinhλ(ξi-ξn)]H(ξi-ξn)
(35)
对于简支-固支边界条件
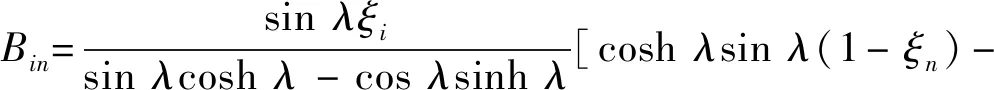
[sinλ(ξi-ξn)-sinhλ(ξi-ξn)]H(ξi-ξn)
(36)
对于固支-固支边界条件
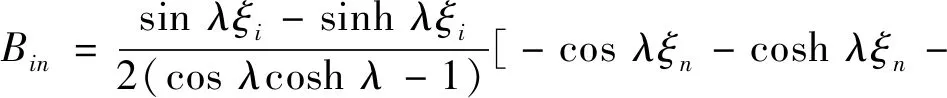
[sinλ(ξi-ξn)-sinhλ(ξi-ξn)]H(ξi-ξn)
(37)
若式(34)有非零解,其系数行列式的值应等于零,此为频率方程。由行列式搜根法可得各阶固有频率参数,将固有频率参数代回式(34),可得各支承反力的相对值,将其代回相应边界条件下的位移函数Y(ξ),即为振型函数。
传统分析方法是将多跨梁沿支承处分段,基于自由振动方程对每段梁元进行求解,然后利用支承处的连接条件得到整个梁的特征方程。本文将支承反力看作是作于梁上的未知外力,利用强迫振动方程进行梁的自由振动分析。本文方法与传统解法只是表达形式上的不同,两者分析结果本质是完全一致的,当支承个数较多时,本文方法更为简单。
5 算例验证
以某多跨高墩桥梁为例,利用Midas Civil 2010软件建立有限元模型,如图9所示。采用空间梁单元模拟主梁与桥墩,根据截面特性划分为960个单元,采用刚性连接模拟支座、墩底固结、主梁两端固支。模型参数为:梁跨径50 m+(2×100)m+50 m,箱梁上、下翼板宽度分别为12.5 m和6.5 m,上、下翼板及腹板厚度分别为0.28 m,0.32 m和0.4 m,混凝土密度2 600 kg/m3,弹性模量3.55×104MPa。桥墩采用双肢薄壁空心墩,墩顶截面尺寸6.5 m×6.5 m,壁厚0.7 m,纵桥向放坡系数1∶100,弹性模量3.45×104MPa,墩高依次为50 m,80 m和50 m。支座采用板式橡胶支座,截面尺寸3.5 m×3.5 m,支座厚0.5 m,弹性模量495 MPa,剪切模量1.05 MPa。
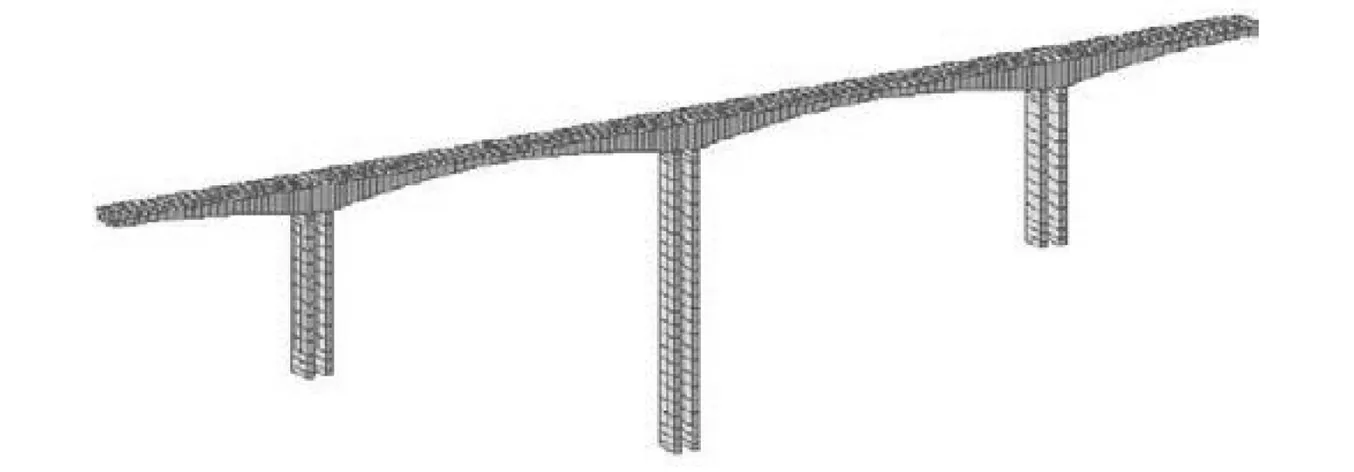
图9 有限元模型Fig.9 Finite element model
取根部梁高与中跨梁高的比值h1/h2作为梁截面变化率,表2、表3给出了梁截面变化率h1/h2分别取2,3,4(h1=4 m,h1=6 m,h1=8 m,h2=2 m)时,主梁竖向振动与横向振动时前四阶固有频率ω和有限元解(finite element analysis,FEA)的比较。由表2可知:理论解和有限元解吻合较好,两者误差随截面变化率的变大略有增加,但最大误差为3.5%,不超过5%,验证了本文方法对分析不同截面变化率下的梁都有较高精度。
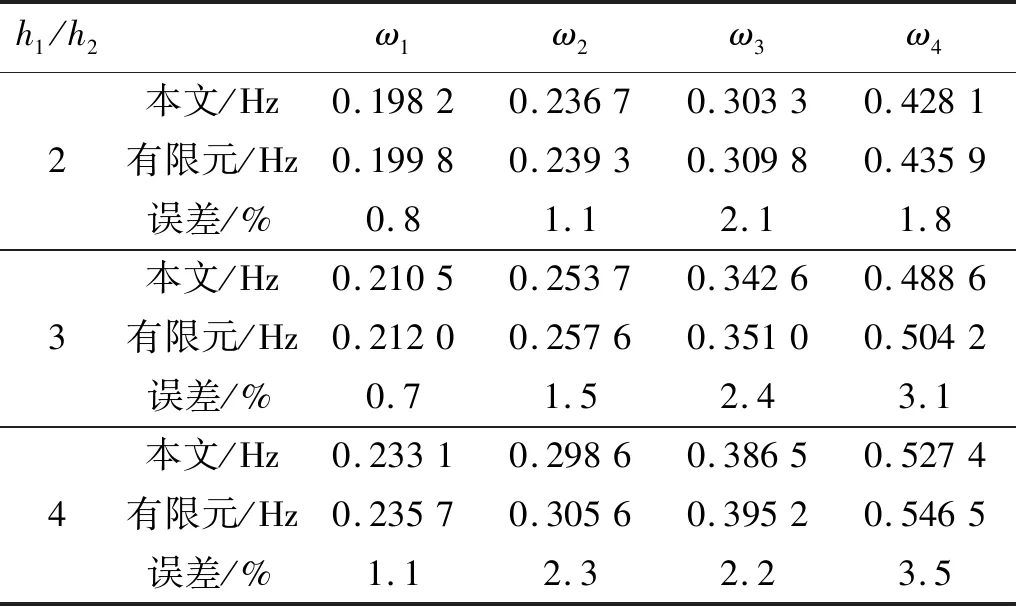
表2 竖向振动计算结果与有限元的比较Tab.2 Comparison of results of vertical vibration with those from FEA
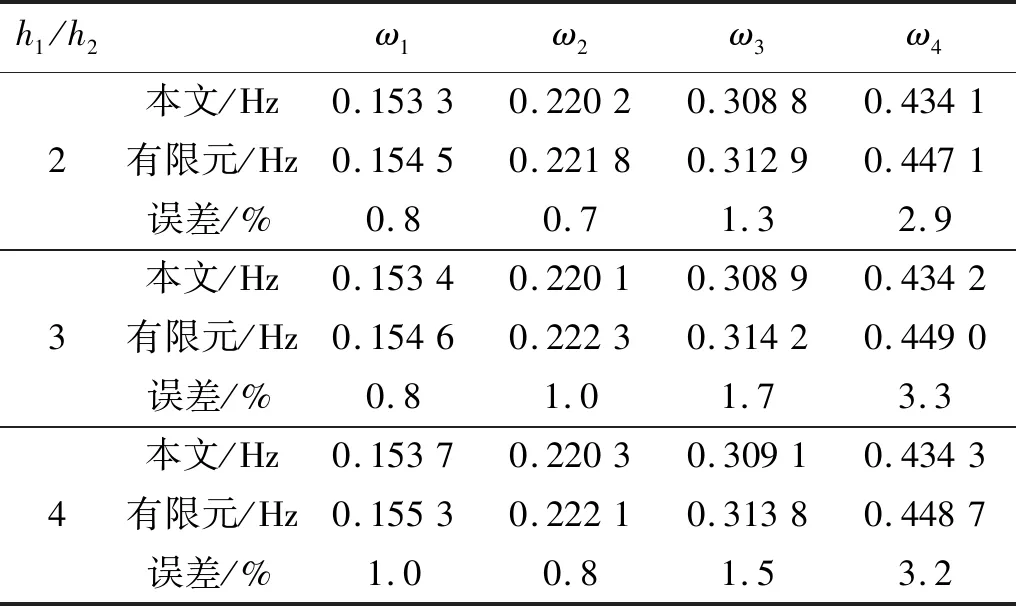
表3 横向振动计算结果与有限元的比较Tab.3 Comparison of results of transverse vibration with those from FEA
6 参数分析
以两端简支的等距两跨桥为例,分析梁截面变化率h1/h2与桥墩高度H对主梁频率参数λ的影响。梁截面变化率对主梁竖向振动与横向振动频率参数的影响,如图10、图11所示。由图10、图11可知:竖向振动时频率参数随着梁截面变化率的增大而增大,本文假定梁高二次抛物线变化而横向梁宽不变,故截面变化率对横向振动频率参数影响较小。给出了桥墩高度对主梁竖向振动与横向振动频率参数的影响,如图12、图13所示。由图12、图13可知:频率参数随着桥墩高度的增大而减小,且各阶频率参数减小的速率不同。
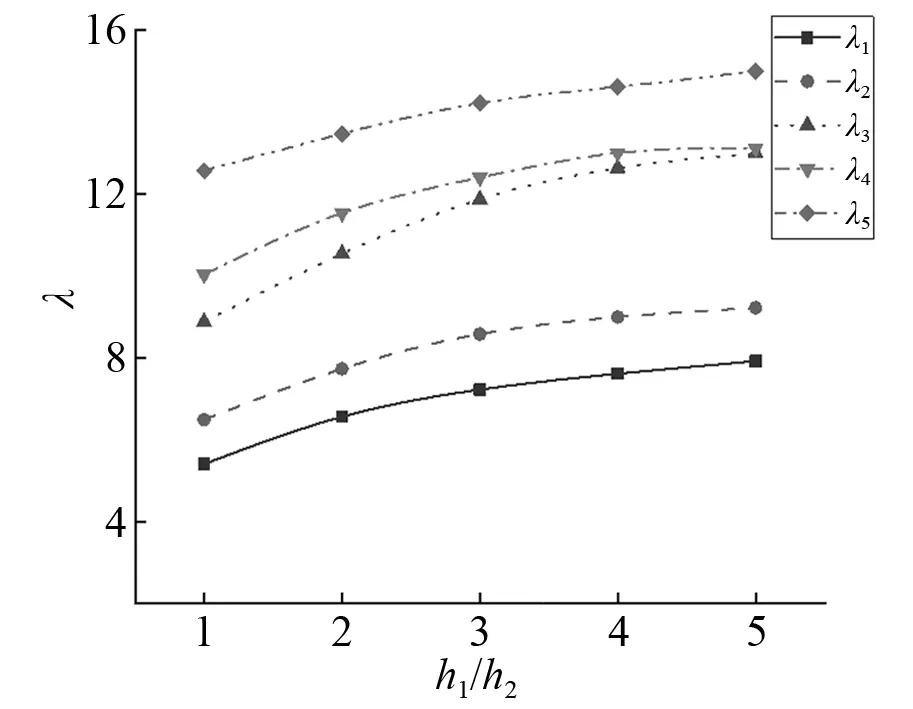
图10 不同截面变化率下主梁竖向振动频率参数Fig.10 Vertical vibration frequency parameters of the beam with different cross-section change rates
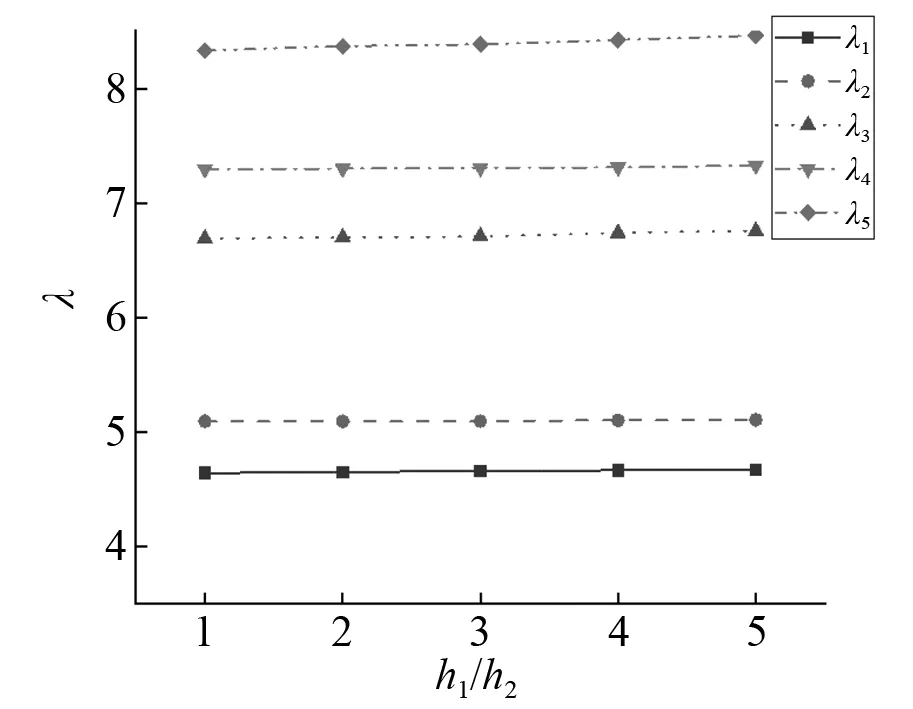
图11 不同截面变化率下主梁横向振动频率参数Fig.11 Transverse vibration frequency parameters of the beam with different cross-section change rates
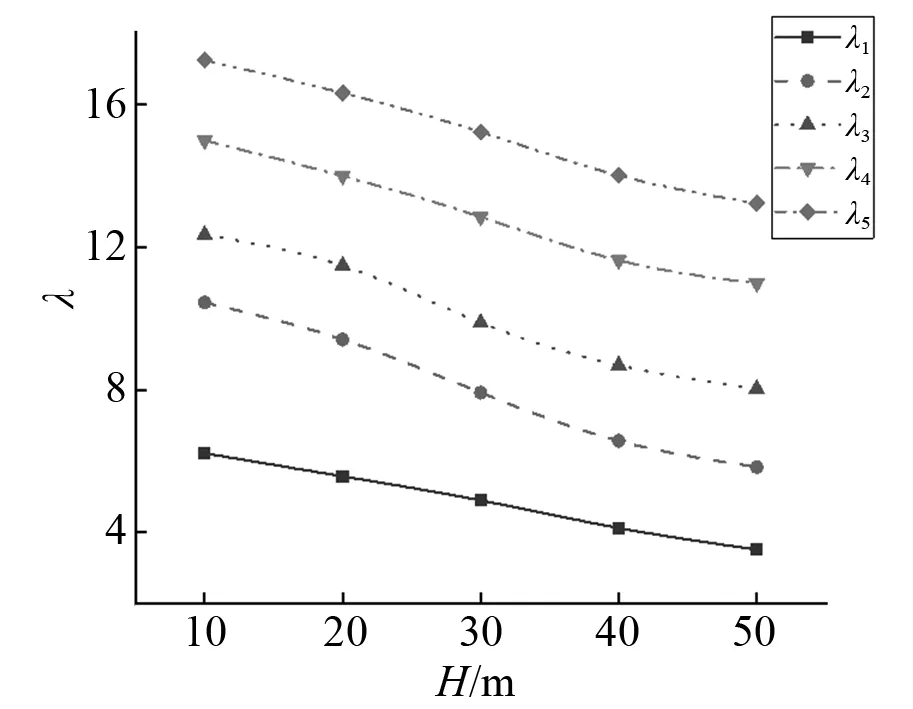
图12 不同桥墩高度下主梁竖向振动频率参数Fig.12 Vertical vibration frequency parameters of the beam with different pier heights
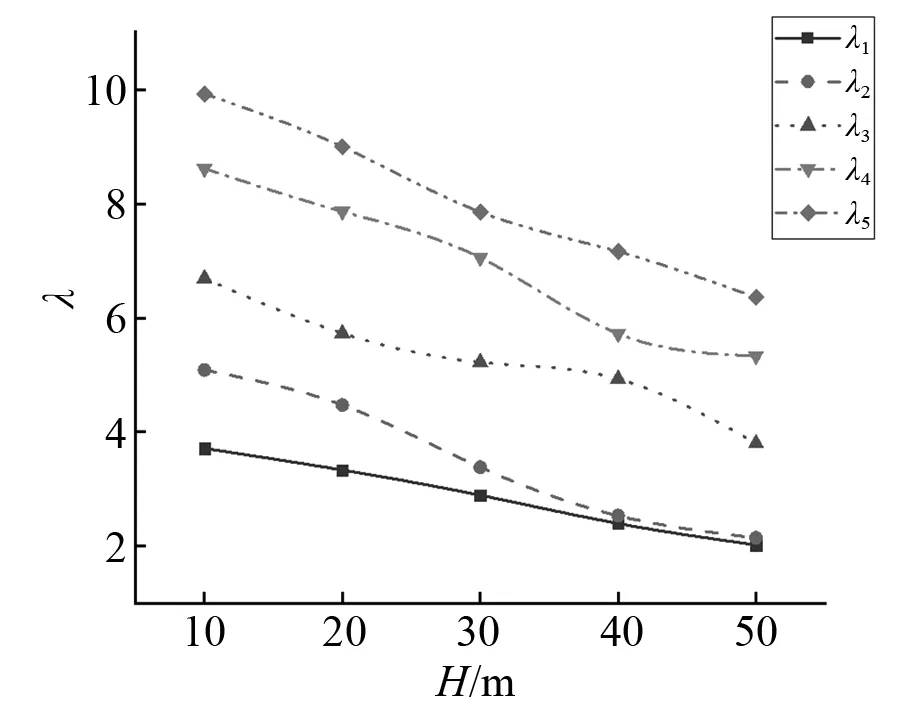
图13 不同桥墩高度下主梁横向振动频率参数Fig.13 Transverse vibration frequency parameters of the beam with different pier heights
分析梁截面变化率与桥墩高度对主梁振型的影响。当梁截面变化率h1/h2分别取2,3,4,5时,主梁竖向振动时前二阶振型图,如图14、图15所示。由图14、图15可知:位移振型值随着梁截面变化率的增大而减小,与一阶振型相比,二阶振型变化幅度显著降低,即高阶振型对梁截面变化敏感性下降。不同梁截面变化率下主梁横向振动时前二阶振型图,如图16、图17所示。由图16、图17可知:梁截面变化对横向振型几乎没有影响,这是由于本文假定梁截面横向宽度保持不变,故截面变化对横向振型影响较小。当桥墩高度H分别取20 m,30 m,40 m和50 m时,主梁竖向振动与横向振动时前二阶振型图,如图18~图21所示。由图18~图21可知:竖向位移振型值与横向位移振型值均随桥墩高度的增大而增大,二阶振型变化幅度低于一阶振型,即低阶振型对桥墩高度敏感性较大。
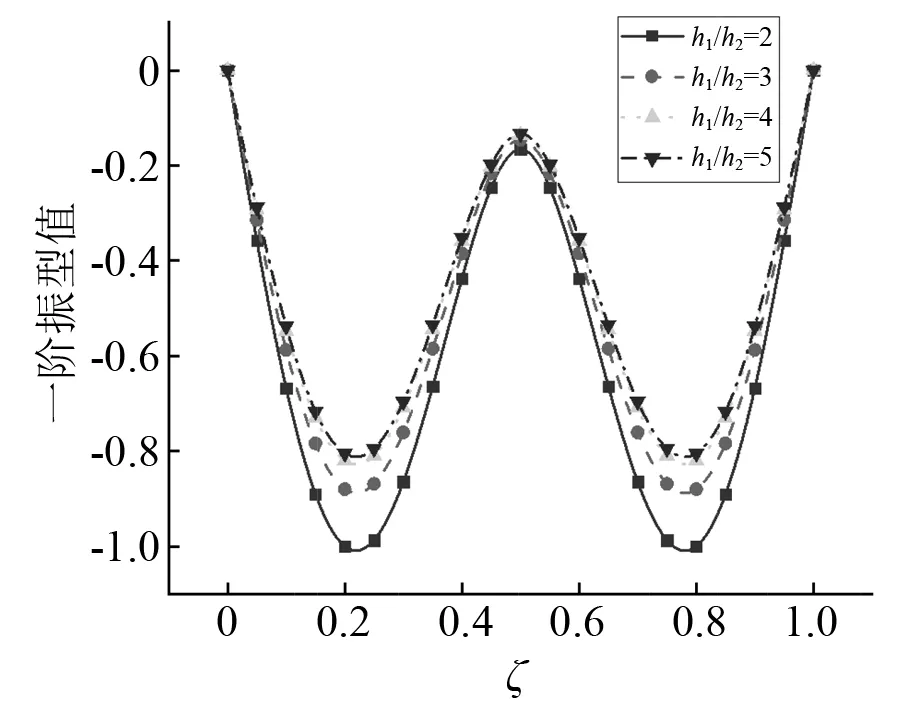
图14 竖向振动第一阶振型Fig.14 The first mode shape of vertical vibration
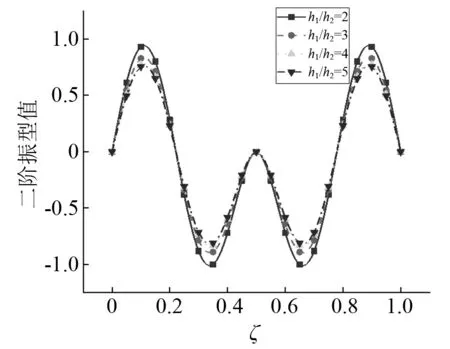
图15 竖向振动第二阶振型Fig.15 The second mode shape of vertical vibration
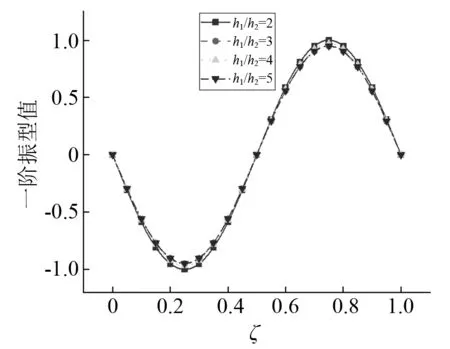
图16 横向振动第一阶振型Fig.16 The first mode shape of transverse vibration
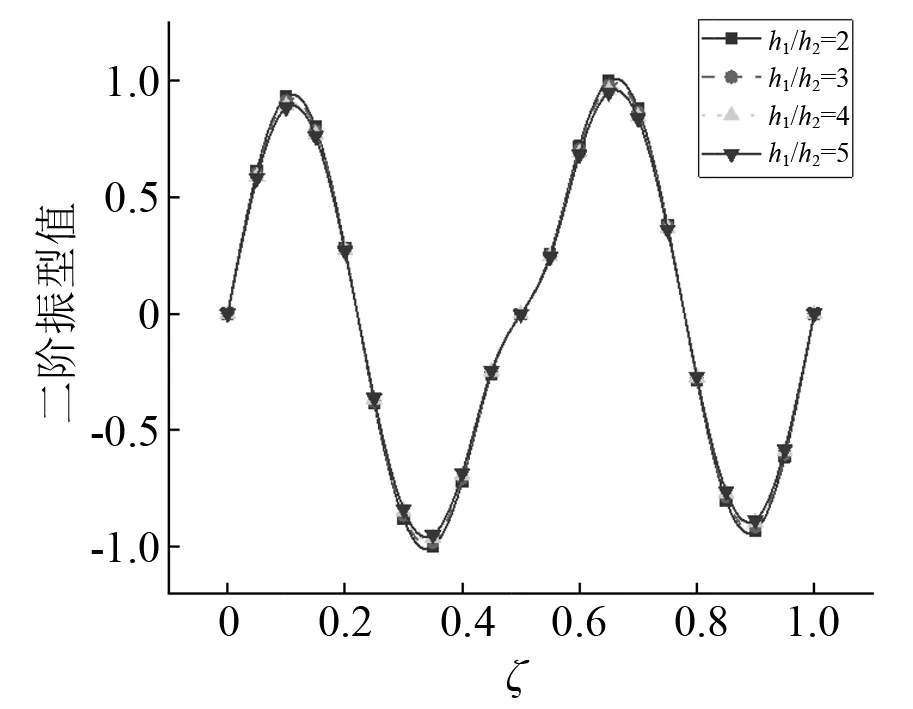
图17 横向振动第二阶振型Fig.17 The second mode shape of transverse vibration
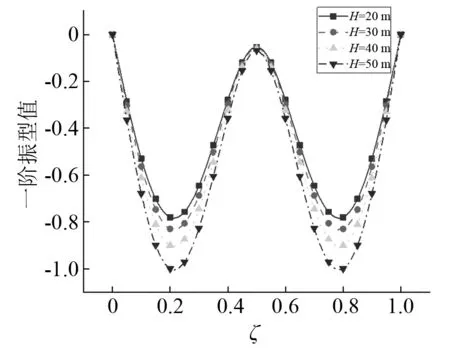
图18 竖向振动第一阶振型Fig.18 The first mode shape of vertical vibration
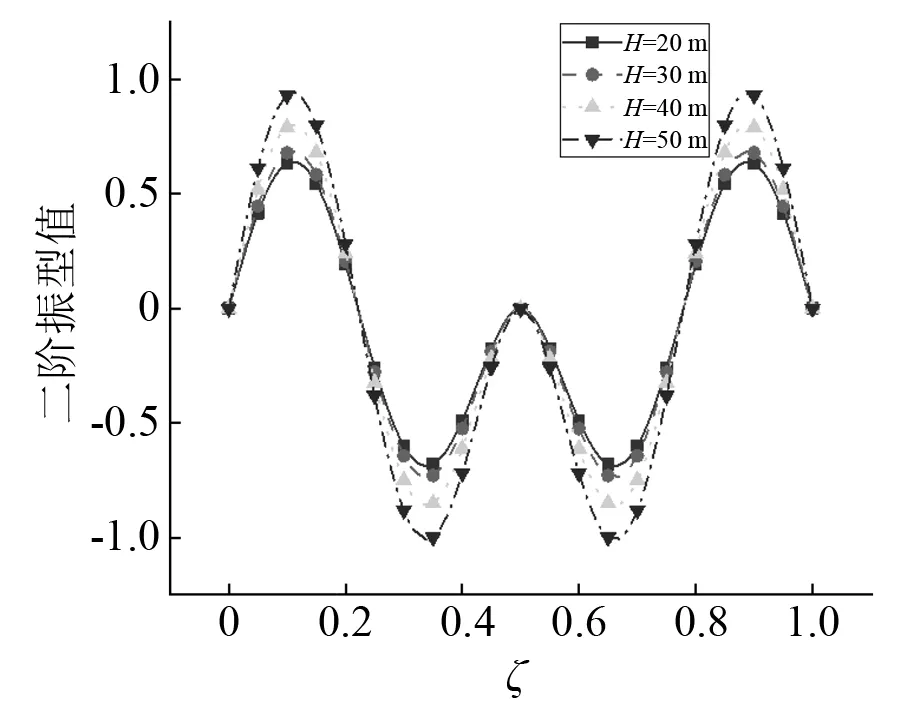
图19 竖向振动第二阶振型Fig.19 The second mode shape of vertical vibration
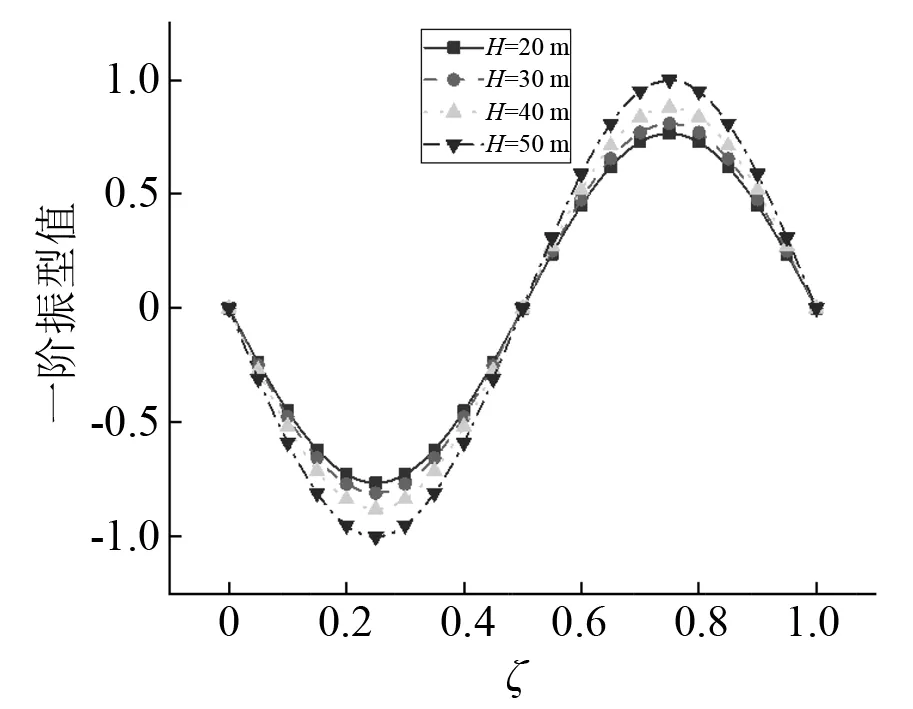
图20 横向振动第一阶振型Fig.20 The first mode shape of transverse vibration
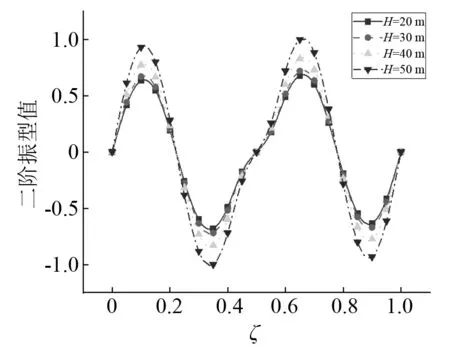
图21 横向振动第二阶振型Fig.21 The second mode shape of transverse vibration
7 结 论
本文基于Euler-Bernoulli梁理论,将多跨高墩变截面梁桥振动问题转化为多跨弹性支承直梁的动力学特性研究,得到如下结论:
(1)计算梁截面等效面积与等效惯性矩,用等截面梁微分方程求解变截面梁固有频率及振型,降低了方程求解难度,在保证计算精度的同时,具有分析简单直接的特点。
(2)当支承个数较多时,将弹性支承反力看作是梁上未知外力,利用强迫振动方程进行梁的自由振动分析,比传统分析方法简单。
(3)梁截面变化率对主梁竖向振动影响较大,对横向振动影响较小。
(4)主梁固有频率随桥墩高度增大而减小,位移振型值随桥墩高度增大而增大。
