求解声学问题的元胞自动机方法
2021-09-27汪振国
罗 锟,汪振国
(1.华东交通大学 铁路环境振动与噪声教育部工程研究中心,南昌 330013;2.大连理工大学 土木工程学院,辽宁 大连 116024)
在建筑结构、交通运输、工程机械等诸多领域,噪声污染问题一直受到广泛关注[1],研究准确有效的声学数值计算方法是噪声预测和控制技术发展的基础,也是解决噪声污染问题的关键步骤。当前,已有许多成熟的数值计算方法在声学领域得到应用,例如:有限元法[2-3]、边界元法[4-5]、统计能量法[6-7]、多方法联合求解[8-10]等。然而,适于描述复杂动力系统的元胞自动机(cellular automata,CA)方法在声学系统的建模和计算方面却鲜有应用。
CA自其诞生至今,已衍生出几种独立在CA模型之外的计算模型,如格子气自动机(lattice gas automata,LGA)模型、格子Boltzmann模型、多粒子模型等,且在各种物理问题的建模上均有应用[11]。在模拟波传播方面:Leamy[12]介绍了一种在理想化线弹性介质中利用Moore型邻居CA方法模拟地震波的传播行为;Nishawala等[13]结合毗域动力学与CA方法对弹性波传播进行模拟,结果显示CA计算值与解析解吻合较好;Krutar等[14-15]利用LGA模型模拟了波浪现象,并探讨了复杂场景下水中声传播和散射问题;Sudo等[16-17]在此基础上,进一步改进LGA模型,提出声传播的一维和二维LGA模型,其中二维声传播模型虽求解稳定,但计算结果存在各向异性色散;Komatsuzaki等[18]利用CA模型模拟了一维和二维声传播现象,其中二维CA模型采用Von Neumann型邻居,这导致元胞状态变量在每一计算步中出现各向异性更新的问题,从而二维CA计算结果与解析解间存在较大差异。可以发现,若要应用CA方法对声学问题进行准确求解,则必须解决元胞各向异性更新的问题。
本文首先应用CA原理,结合声波方程导出一维声学CA模型的局部演化规则,并对声管声场进行建模,同时考虑两种边界条件,利用一维CA模型计算管内声压分布,并将结果与解析解进行对比验证;之后,以脉动球源声场为分析对象,按球坐标下的二维声波方程导出Y函数一维CA模型的局部演化规则,进而利用Y值与声压值间的关系建立二维脉动球源声场的CA模型,并计算球源声辐射性质;最后对比分析二维CA结果与解析解。
1 CA理论及其声学模拟
CA是一种离散化的动力系统,其由元胞、元胞空间、邻居、状态变量、局部演化规则和边界条件等部分组成[19],如图1所示。

图1 元胞自动机系统Fig.1 Cellular automata system
对于某一具体问题,应用CA方法往往需要将计算区域在时间和空间上进行离散,每一离散单元称为元胞或元胞单元,所有元胞组成的集合就是元胞空间;状态变量通常为需求解的数或数集,每一个元胞内都对应着状态变量,且在不同时刻下实时更新;对于一个元胞来说,其周围相邻的且在单位时间步内参与演化的元胞为其邻居,如图2所示。一维CA系统邻居通常以半径R为认定准则,即在半径R以内的元胞均为该元胞的邻居,二维CA系统邻居类型多样,其中Von Neumann型与Moore型最为常见;CA系统的边界条件按所求解问题的实际边界条件进行模拟。
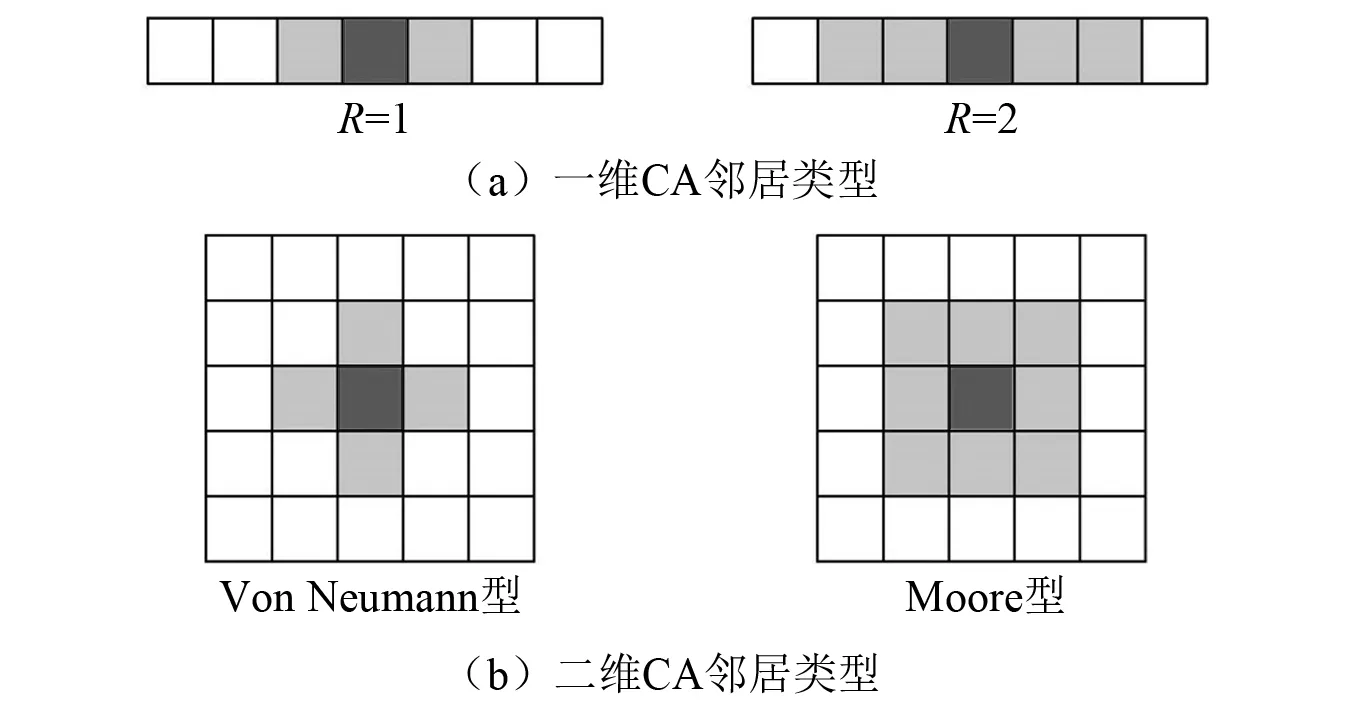
图2 CA系统邻居类型Fig.2 Neighbor types of CA system
局部演化规则是CA系统中最为重要的组成部分,它能够由当前时刻元胞及其邻居的状态变量确定出下一时刻元胞的状态变量,简单来讲,局部演化规则就是一组状态转移函数,其表达式为
(1)
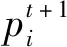
应用CA方法求解声学问题的一般步骤是:首先需分析声源及其辐射声场特性,明确声学CA模型的维度和邻居类型;之后对计算区域进行元胞单元划分,并确定元胞尺寸和时间步长,同时以声压为状态变量,考虑辐射声场的声学边界条件,并按声波方程导出局部演化规则;最后构建声学CA模型进行求解。
2 一维声学CA模型
2.1 局部演化规则
声传播的一维声波方程为
(2)
式中:p为x,t的声压函数;c为声速。
定义元胞单元尺寸为Δx,时间步为Δt,在任意t时刻,式(2)的差分形式为
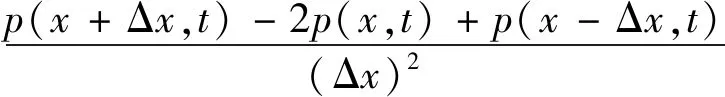
(3)
定义局部演化系数
φ=(c·Δt/Δx)2
(4)
将式(4)代入式(3)并化简可得
p(x,t+Δt)=φ{p(x+Δx,t)+p(x-Δx,t)+[(2/φ)-2]p(x,t)-(1/φ)p(x,t-Δt)}
(5)
从式(5)可以看出:x位置处元胞t+Δt时刻的声压值与其左、右两相邻位置x+Δx,x-Δx元胞t时刻声压和该元胞t-Δt时刻声压相关,因此邻居类型为R=1型,如图3所示。同时,因为CA模型中声传播速度ca等于声速c,所以局部演化系数
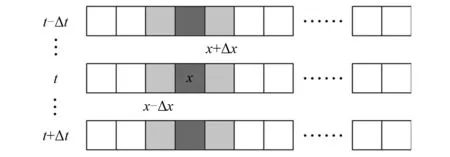
图3 一维声学CA模型邻居Fig.3 Neighbors of 1D acoustic CA model
φ=(c·Δt/Δx)2=(c/ca)2=1
(6)
那么式(5)可进一步简化为
p(x,t+Δt)=p(x+Δx,t)+p(x-Δx,t)-p(x,t-Δt)
(7)
式(7)即为一维声学CA模型的局部演化规则。
2.2 管道声学CA模拟
设有l=2 m长声管,管体为刚性壁,其法向振速为0,入射压力波与管道平行,管内声波以平面波的形式传播,在传播过程中不发生径向粒子的振动,所以管内声场可由一维CA模型模拟,如图4所示。通过考虑两种边界条件来确定管中声压分布规律:①左端激励,右端开口;②左端激励,右端刚壁。
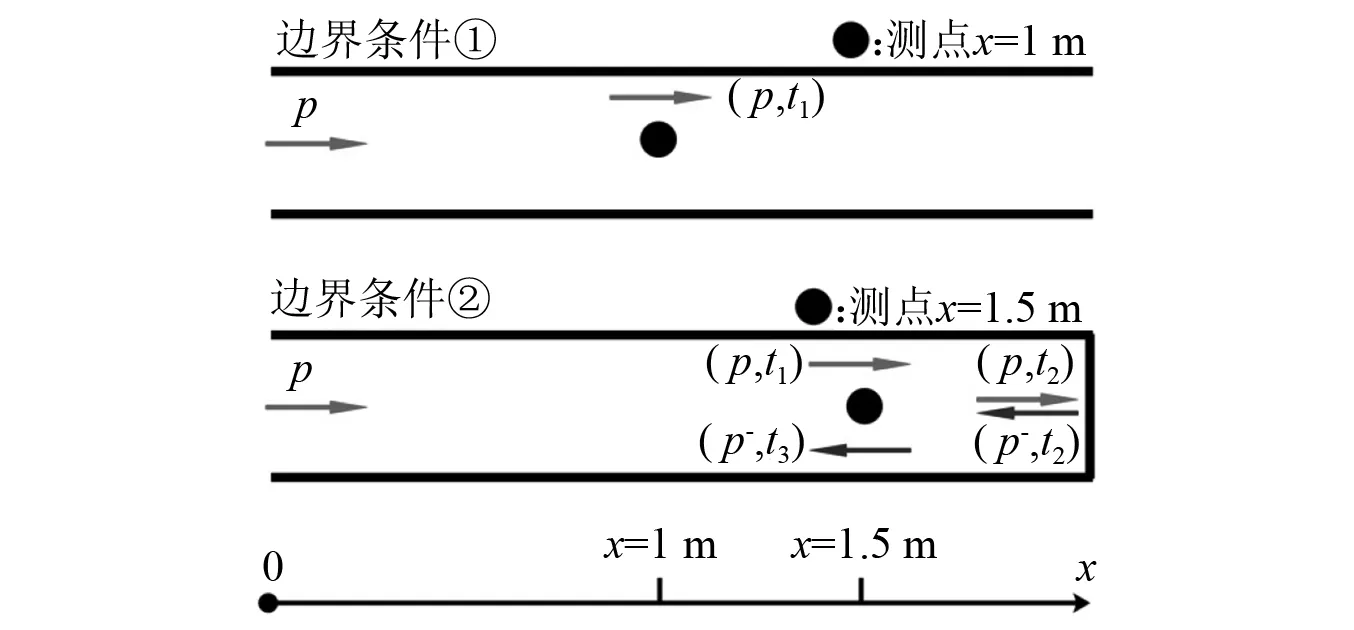
图4 声管边界条件Fig.4 Boundary conditions of acoustic tube
在边界条件①的声管中,选择x=1 m处为测点,入射声波p在t1时刻到达该位置,则该测点声压解析解的表达式为
p(x,t)=p0ei(ωt-kx+θ)
(8)
式中:p0为声压幅值;ω为圆频率;k为波数;θ为位相。
在边界条件②的声管中,选择x=1.5 m处为测点,入射声波p在t1时刻到达该位置,在t2时刻到达末端刚壁并发生反射,形成沿-x向的反射声波p-,p-在t3时刻到达测点处,此时开始,测点将处于p与p-的合成声场中。该测点声压解析解的表达式为
(9)
将管内声场沿x向离散成单元尺寸Δx=1 mm的元胞,以式(7)为局部演化规则,建立一维声学CA模型,对两种边界条件下管内声场声压进行求解,将计算结果与解析解对比,如图5所示。计算参数如表1所示。
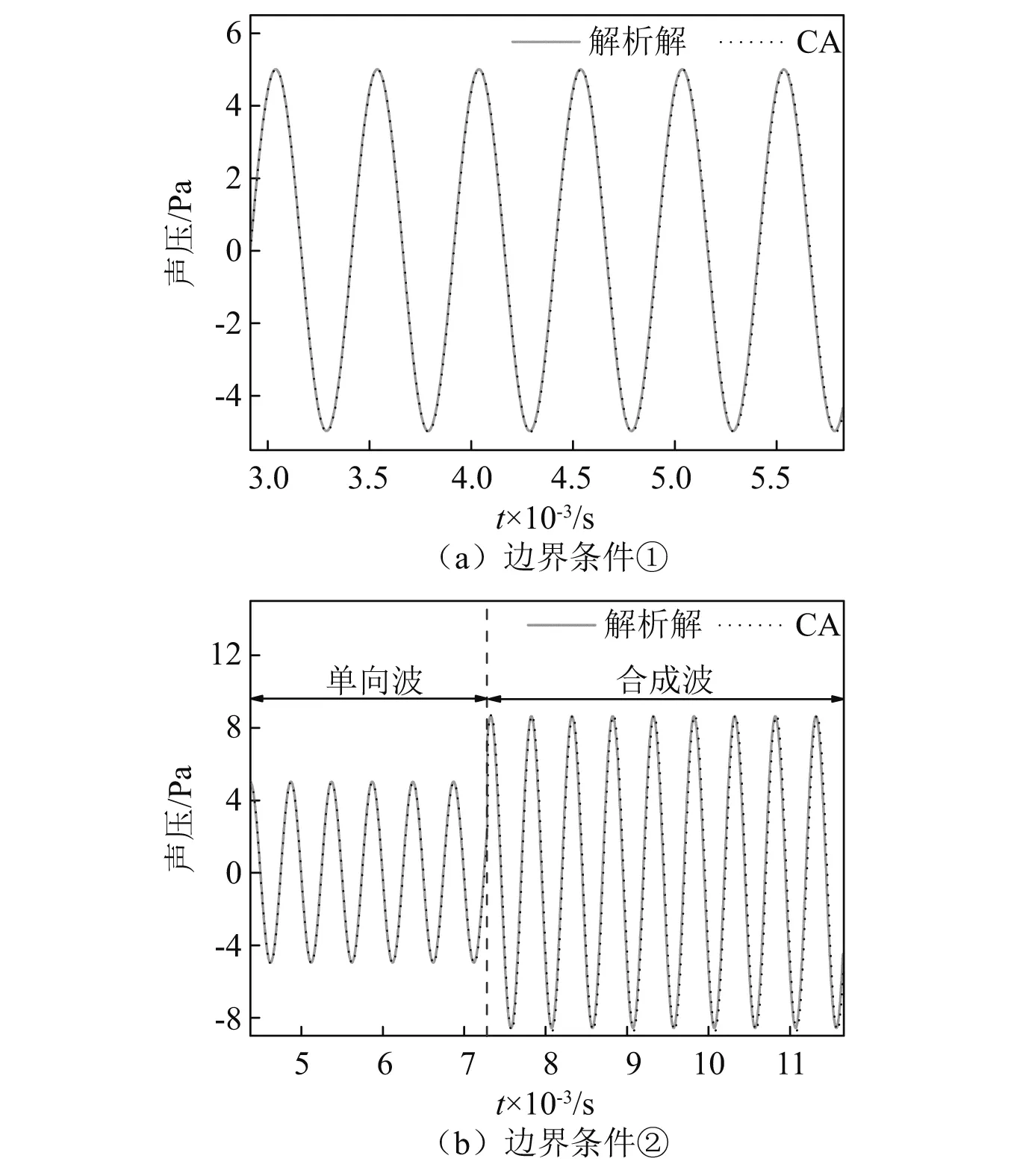
图5 声管测点声压时程曲线Fig.5 Sound pressure time history curve of measuring points in acoustic tube

表1 计算参数Tab.1 Calculation parameters
由图5可知:两种边界条件下的CA模型计算结果与解析解吻合良好,单向平面波场最大误差仅为0.614%,合成平面波场最大峰值误差为1.048%,这表明声学CA模型能够准确模拟平面波场声压分布,且计算结果可靠。
在边界条件②下,声管的共振频率f为
f=mc/2l
(10)
式中:m为阶数,m=1,2,…;c为声速;l为管长;当入射声波频率为前3阶共振频率时,管内声压分布,如图6所示。
从图6可知:声学CA模型能够模拟声共振现象,当在自然频率附近激发正弦波时,合成声场会出现驻波,图5(b)中合成波幅值不等于10 Pa,这是因为入射波频率为2 000 Hz,介于共振频率第23阶(1 972.25 Hz)~第24阶(2 058.25 Hz)。
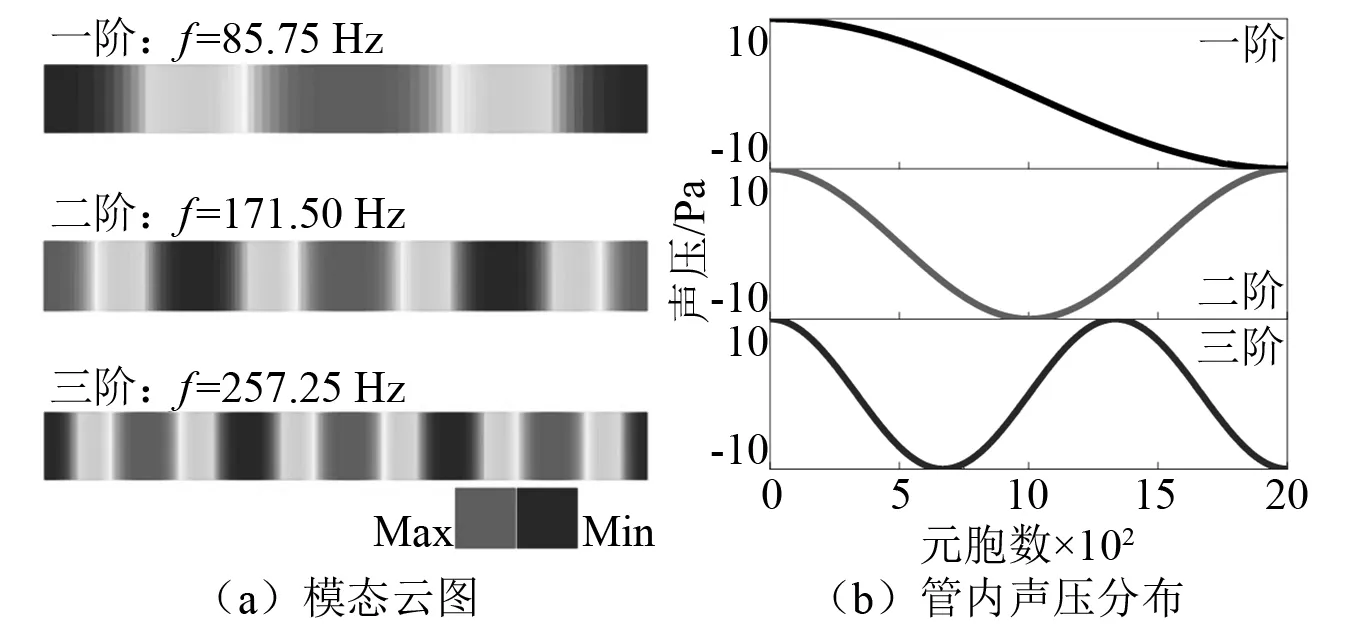
图6 声模态Fig.6 Acoustic modes
3 二维声学CA模型
3.1 Von Neumann型CA局部演化规则
声传播的二维声波方程为
(11)
式中:p为x,y,t的声压函数;c为声速。
定义元胞单元尺寸为Δx=Δy=Δl,时间步为Δt,局部演化系数φ=(c·Δt/Δl)2,在任意t时刻,式(11)的差分形式可变化为
p(x,y,t+Δt)=φ{p(x+Δx,y,t)+p(x-Δx,y,t)+
p(x,y+Δy,t)+p(x,y-Δy,t)+
2[(1/φ)-2]p(x,y,t)-(1/φ)p(x,y,t-Δt)}
(12)
从式(12)可知:(x,y)位置处元胞t+Δt时刻的声压值与其上、下、左、右4处相邻位置(x,y+Δy),(x,y-Δy),(x-Δx,y),(x+Δx,y)的元胞t时刻声压和该元胞t-Δt时刻声压相关,因此邻居类型为Von Neumann型,如图7所示。
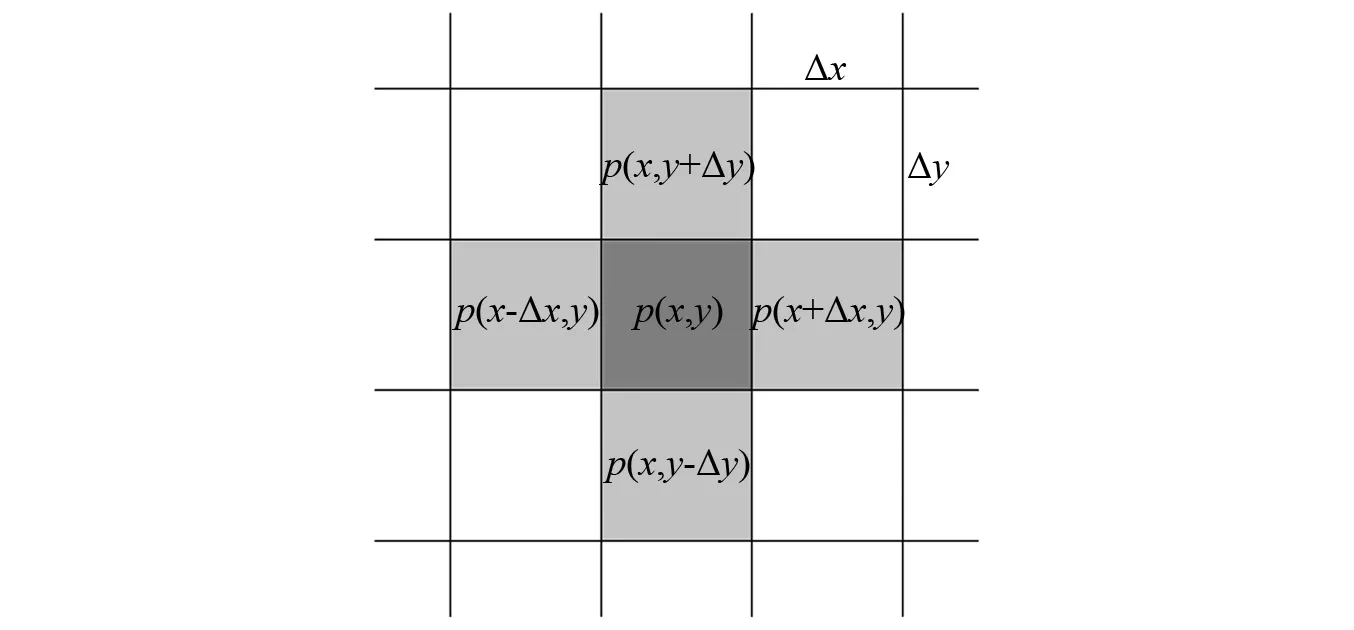
图7 二维声学CA模型邻居Fig.7 Neighbors of 2D acoustic CA model
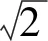
φ=(c·Δt/Δl)2=(c/ca)2=1/2
(13)
将式(13)代入式(12),可得Von Neumann型二维声学CA模型的局部演化规则
p(x,y,t+Δt)=0.5{p(x+Δx,y,t)+
p(x-Δx,y,t)+p(x,y+Δy,t)+p(x,y-Δy,t)}-p(x,y,t-Δt)
(14)
Komatsuzaki等的研究曾利用Von Neumann型CA求解点声源自由空间的辐射声场,声场中过点源的某一切片结果,如图8所示。由图8可知:在声源附近和离声源较远位置处,解析解和CA解相差不大,但是在离声源一定距离的位置上,解析解与CA解相差很大,最大误差在50%以上,这是由CA模型各向异性的更新规则所致。
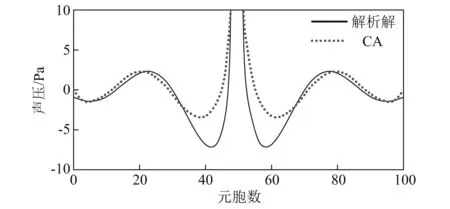
图8 Komatsuzaki等的研究中点源辐射声场声压分布Fig.8 Distribution of sound pressure in the radiated sound field of point source in Komatsuzaki et al research
3.2 脉动球源辐射声场
为解决二维声学CA模型中状态变量更新的各向异性问题,在导出局部演化规则时可将直角坐标变换为球坐标,以脉动球源为例,坐标原点取在球心,其球坐标下的声传播二维声波方程为
(15)
式中:r为空间任一点至球心的距离;p为r,t的声压函数;S为r处波阵面面积;c为声速。令Y=pr,则式(15)变换为
(16)
可以发现,式(16)与一维声波方程类似,那么应用CA方法求解脉动球源二维声场声压时,可先建立Y函数的一维CA模型,在解出二维声场中任意场点的Y值之后,只需将Y值比上该场点至球心的距离r即可得到二维声场中任意场点的声压值p。
算例1假设在二维自由空间中存在一个脉动球源,以球心为中心,取10 m×10 m的矩形区域为计算空间,将计算空间以边长为0.1 m的正方形网格划分为100×100个像元,计算参数如表2所示。自由空间脉动球源声场声压解析解表达式为

表2 计算参数Tab.2 Calculation parameters
(17)
式中:ρ为介质密度;k为波数;r0为球源半径;u为球源振速幅值;θ按式(18)计算
θ=arctan(1/kr0)
(18)
将计算区域声压分布解析解与球坐标下的CA解对比,如图9所示。二维自由空间计算区域内竖向和对角切片的声压分布,如图10所示。
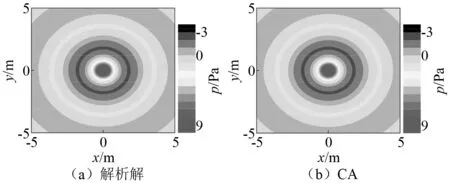
图9 自由空间脉动球源辐射声压云图Fig.9 Nephograms of sound pressure radiated by pulsating sphere source in free space
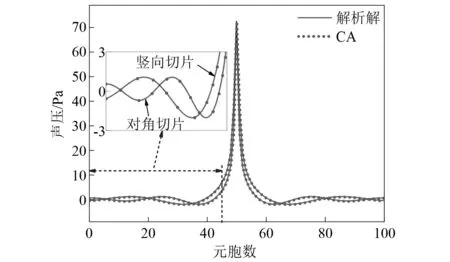
图10 竖向与对角方向声压分布Fig.10 Distribution of sound pressure in vertical and diagonal directions
由图9和图10可知:CA结果显示,二维脉动球源在自由空间内的声辐射形状为圆周,且声压随距离r的增大而减小,近场声压衰减快,远场声压衰减慢,这与球源辐射声场性质一致;解析解与CA解吻合良好,表明本文所建立的二维CA模型能准确求解脉动球源自由空间声辐射问题;采用球坐标声波方程导出Y函数一维CA模型局部演化规则,进而求解二维声场声压的方法,可避免二维CA模型中元胞状态变量各向异性更新的问题。
算例2假设在二维半自由空间中存在一个脉动球源1,距离球源下方5 m处有一无限大刚性壁面,以球心为中心,取10 m×10 m的矩形区域为计算空间,将计算空间以边长为0.1 m的正方形网格划分为100×100个像元,如图11所示。计算参数如表2所示。由镜像原理可知,半自由空间脉动球源1声场等效于自由空间脉动球源1及其沿刚壁镜像球源2声场的叠加,此时声场声压解析解表达式为
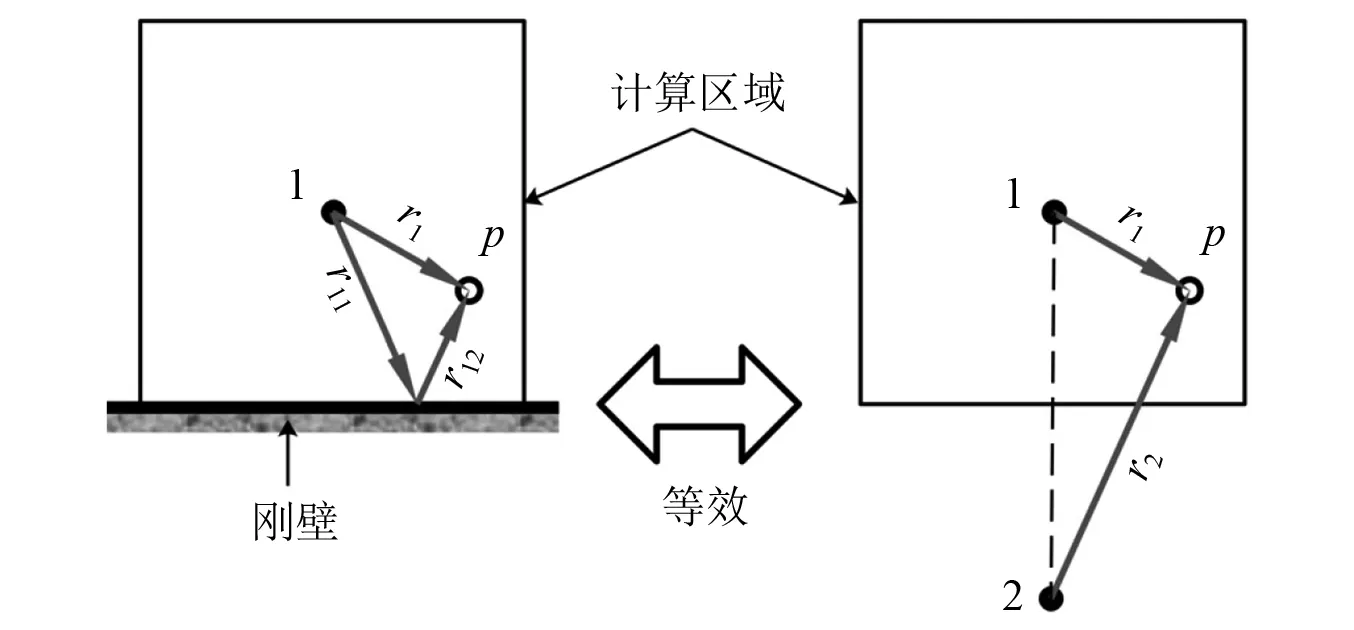
图11 半自由空间脉动球源辐射声场Fig.11 Sound field radiated by pulsating sphere source in half free space
(19)
其中,
(20)
将计算区域声压分布解析解与CA解对比,如图12所示。二维半自由空间计算区域内横向、竖向和对角切片的声压分布,如图13所示。
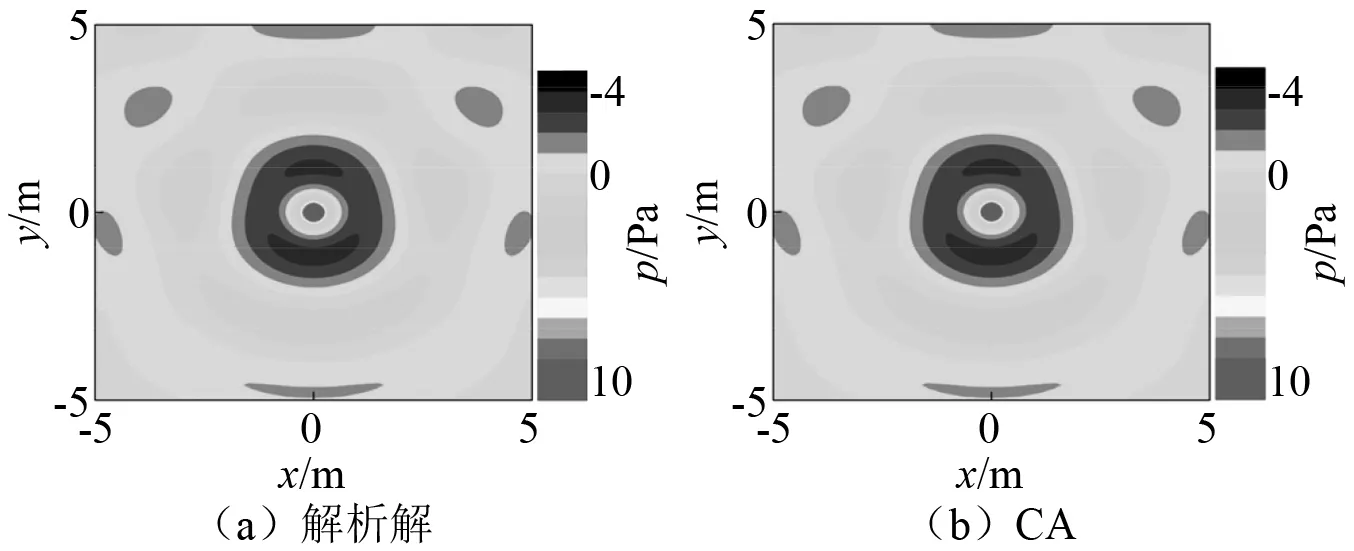
图12 半自由空间脉动球源辐射声压云图Fig.12 Nephograms of sound pressure radiated by pulsating sphere source in half free space
由图12与图13可知:解析解与CA解吻合良好,表明本文所建立的二维CA模型能准确求解脉动球源半自由空间声辐射问题;同时也说明了对于双球源组合声场,该模型依旧具有较高的计算精度和良好的适用性。
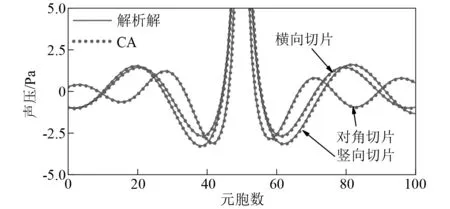
图13 横向、竖向与对角方向声压分布Fig.13 Distribution of sound pressure in transverse,vertical and diagonal directions
4 结 论
本文利用CA方法对声管和脉动球源声学问题进行建模,分析了一维平面波与二维球面波声场规律,并将声学CA模型计算结果与解析解进行对比,得到以下几点结论:
(1)本文建立的声学CA模型能准确模拟平面波与球面波场声辐射规律,且结果与声波方程的解吻合程度高。
(2)一维CA模型的局部演化规则可直接由声波方程导出;而直接按声波方程导出二维CA模型的局部演化规则会使元胞状态变量更新存在各向异性的问题。
(3)采用球坐标声波方程导出脉动球源Y函数一维CA模型的局部演化规则,进而求解二维声场声压的方法,可避免二维CA模型中元胞状态变量各向异性更新的问题。
(4)对于双球源组合声场,声学CA模型依旧具有较高的计算精度和良好的适用性;那么对于多点源组合成的面声源辐射声场,利用CA方法分析其声场性质是否可行,这将在下一步工作中继续探讨。
