基于混凝土细观模型的高压状态方程数值模拟研究
2021-09-27李昊阳孔祥振
李昊阳,孔祥振,2,方 秦,彭 永,崔 健
(1.陆军工程大学 国防工程学院,南京 210007;2.东南大学 土木工程学院,南京 211189;3.国防科技大学 文理学院,长沙 410073;4.天津大学 建筑工程学院,天津 300072)
混凝土材料广泛应用于军用和民用工程结构中,当受到炸药爆炸和弹体侵彻等强动载作用时,近区混凝土处于10 GPa量级的高围压状态,混凝土呈现近似流体特性,但仍具有明显的剪切强度[1]。在流体动力学软件中,为较好描述上述高围压特性,材料动态力学行为对于偏量和球量分别处理,应力偏量和应变偏量之间的关系描述了材料的剪切行为,通过本构关系(或破坏面)表示;而应力球量和应变球量的关系描述了材料的压缩行为,通过高压状态方程(equation of state,EoS)表示。因此混凝土材料高压状态方程的准确性对于描述其高围压下的压缩行为至关重要[2]。
当前获得混凝土高压状态方程实验手段主要有3类:静水压缩实验、平板撞击实验和全尺寸爆炸实验。静水压缩实验通常利用伺服装置施加压力,但受设备限制,所施加的最大静水压力在1 GPa以下[3-4],且实验加载速率在准静态水平,与强动载下的高应变率不符。平板撞击实验通常利用轻气炮发射金属高速飞片撞击混凝土试件并产生强间断波,通过记录混凝土试件中冲击波速和粒子速度,结合Rankine-Hugoniot方程,进而得到混凝土的高压状态方程。Hall等[5-8]通过平板撞击实验,得到了不同类型混凝土的高压状态方程,但受轻气炮口径限制,飞板和混凝土试件尺寸较小(上述实验中混凝土试件直径约为50 mm、厚度约为15 mm),难以反映混凝土中粗骨料(通常粒径在10~25 mm)引起的非均质性。全尺寸爆炸实验可采用较大尺寸混凝土试件以充分考虑混凝土的非均质性,通过测量炸药爆炸在混凝土试件中产生冲击波的传播得到高压状态方程。Rinehart等[9-10]通过全尺寸爆炸实验得到了混凝土高压状态方程,但炸药爆炸产生的振动会对测量设备造成较大影响,使得测量稳定性不易控制。此外,平板撞击实验和全尺寸爆炸实验费时耗力,难以对各组分性质(如水灰比、骨料级配和体积率等)对高压状态方程的影响进行精细化系统研究。
利用基于混凝土细观模型的数值模拟方法确定高压状态方程,可同时解决平板撞击实验存在的非均质性和全尺寸爆炸实验存在的测试稳定性问题,且易于进行参数分析,明确各组分对高压状态方程的影响规律。该方法通常在细观尺度上将混凝土看作粗骨料、砂浆及其胶结面ITZ(interfacial transition zone)三相介质,通过明确各组分的物理力学特性进而对宏观尺度的混凝土力学行为进行描述。上述基于细观模型的数值模拟方法已广泛应用于强动载下混凝土材料的动态拉伸破坏[11]、动态尺寸效应[12-13]和冲击波传播衰减规律[14-15]的研究。对于本文研究的高压状态方程,考虑到冲击压缩过程中ITZ作用有限,因此可将混凝土看作由骨料和水泥石组成的两相介质。基于两相介质的细观模型,Riedel等[16]通过在混凝土试件上施加不同粒子速度,得到了常规和高强两种不同砂浆组成的混凝土高压状态方程,但其将骨料形状简化为球形,不能反映真实的骨料形状。通过对比基于上述细观模型得到的高压状态方程与已有宏观尺度上的高压状态方程(AUTODYN软件中自动生成的P-α状态方程),Gebbeken等[17]对上述方法进行了验证,进一步探讨了3种不同粒径骨料对高压状态方程的影响。为考虑混凝土中自由水对其高压状态方程的影响,Huang等[18]通过有效应力和混合法则两种方法将自由水引入水泥石高压状态方程中,得到了饱和混凝土的高压状态方程,并发现相比干混凝土,饱和混凝土的高压状态方程斜率(体积模量)更大。上述研究中,最基本假定为破坏面对高压状态方程影响较小,但均未进行系统分析验证该观点,此外研究均局限于单一配合比混凝土,难以推广应用至任意配合比混凝土。
针对已有研究不足并基于Peng等[19]的前期工作,本文首先建立了两相介质混凝土细观模型,通过拟合实验数据确定了骨料的状态方程并采用两种方法(拟合数据和改进的Hugoniot混合法则)确定了水泥石的状态方程;然后基于细观模型得到了混凝土的高压状态方程,并得到了已有实验数据验证,该方法可推广至任意配合比的混凝土材料;最后在此基础上,详细探讨了破坏面参数和水灰比对高压状态方程的影响。
1 高压状态方程
固体高压状态方程描述了材料静水压力、密度和能量三者的变化,用3个维度的空间曲面(Hugoniot曲面)来描述,曲面上的任意一点均代表材料的某一特定状态,如图1(a)所示。对于本文关注的混凝土材料,强冲击(压力10 GPa量级)通常引起的温度和能量变化不大,因此其高压状态方程可简化为二维平面上的压力和密度(用体积应变描述)的关系曲线,如图1(b)所示。混凝土为典型的多孔非均质材料,孔隙变化对高压状态方程影响显著,已有实验数据表明,混凝土高压状态方程表现为3个明显阶段:弹性段、孔隙压实段和密实段,对应的压力分界点分别为PHEL和Plock,其中PHEL为一维平面应变压缩下材料发生非弹性变形对应的压力(通常称为Hugoniot弹性极限)。当压力小于PHEL时材料处于线弹性阶段,超过PHEL后混凝土中的孔隙逐渐坍塌压实且加载体积模量逐渐变大,而当压力超过压实压力Plock时,混凝土孔隙完全压实进入密实状态且体积模量陡增。

图1 固体高压状态方程示意图Fig.1 Schematic diagram of EoS at high pressures of solid materials
固体中冲击波传播的示意图,如图2所示。由于冲击波速Us远超材料粒子速度Up,在相同时间dt内,冲击波阵面传播至3-3,而粒子仅运动至2-2。

图2 一维平面冲击波传播过程Fig.2 One-dimensional plane shock wave propagation process
考虑时间dt极短,波阵面前后物理量可通过质量和动量守恒方程联系,即
ρ0(Us-Up0)=ρ(Us-Up)
(1)
P-P0=ρ0(Us-Up0)(Up-Up0)
(2)
式中:ρ为密度;P为压力;带有下标0的为冲击波阵面(3-3)前;不带下标0的为冲击波阵面(2-2)后,因此在已知Us和Up情况下结合式(1)和式(2)即可得到混凝土的高压状态方程。
2 三维细观模型的建立
考虑到冲击压缩过程中ITZ作用有限,ITZ对材料的影响耦合在水泥石中,因此在细观尺度上将混凝土视为骨料和水泥石组成的两相介质,其中,骨料为粒径大于1 mm的砾石,水泥石包括粒径小于1 mm的细砂、各类孔隙结构和水泥浆。基于Peng等提出的随机骨料生成投放程序,可建立的两相介质几何和有限元模型,如图3所示。该程序主要步骤为:①采用正六面体网格对混凝土试件进行网格划分,并将所有网格单元定义为水泥石;②生成一个随机尺寸的骨料几何模型(采用随机多面体描述)并随机投放进试件中,落入骨料几何范围的网格单元重新定义为骨料;③重复步骤②直至骨料级配及体积率满足要求。

图3 混凝土细观模型示意图Fig.3 Schematic diagram of concrete mesoscopic model
考虑一维应变平面波的传播特性,混凝土细观模型尺寸可根据骨料最大粒径Dmax确定,X和Y(Z)方向尺寸分别为20Dmax和5Dmax。在细观有限元模型一侧施加粒子速度产生冲击波在试件中传播,为达到一维应变状态,施加边界条件约束模型侧表面的Y与Z方向位移,如图4所示。为避免边界效应,测点布置在距Y,Z方向边界的1/5横向尺寸外,同时为避免前后自由表面的影响,模型X方向前后1/5纵向尺寸内不设置测点。
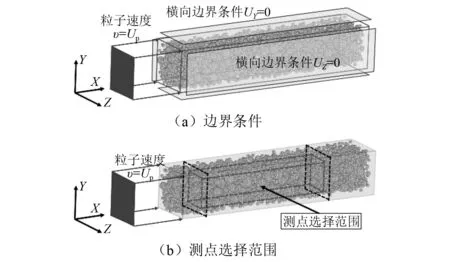
图4 细观数值模拟方法示意图Fig.4 Schematic diagram of mesoscopic numerical simulation method
混凝土中骨料和水泥石波阻抗和材料属性不同,使得冲击波阵面不再为平面,且波阵面后压力和体积应变不均匀是混凝土材料非均质性的体现,因此需在测点区域内尽可能多的选择单元用以表征该不均匀性。对于每次施加粒子速度,取300个单元作为测点,通过平均300个单元的压力和体积应变,得到高压状态方程上的一个点,这样通过施加不同粒子速度,可得到完整的混凝土高压状态方程。
3 材料模型及参数确定
第2章基于细观模型确定高压状态方程的方法准确性取决于骨料和水泥石材料模型的准确性。基于作者前期开发的混凝土类材料的动态损伤材料模型(Kong-Fang模型)[20],本章分别确定骨料和水泥石的破坏面和状态方程。
Kong-Fang材料模型最初提出用以描述冲击爆炸荷载作用下混凝土材料的动态力学性能,该模型为损伤塑性模型,并采用偏量(破坏面)和球量(状态方程)分开处理的方式,并已推广应用到岩石材料[21],以下进行简要介绍。
当前破坏面Y定义为
Y(σij,D)=r′[D(σr-σm)+σm]
(3)
式中:σij为应力张量;r′为当前子午线与压缩子午线的比值;σm和σr分别为压缩子午线上的最大强度面和残余强度面,定义为
(4)
(5)
式中:参数a1和a2通过拟合三轴压缩实验数据确定;fc和T分别为单轴压缩强度和拉伸强度;P为压力;ψ为拉伸和压缩子午线比率;D为损伤指数,D=1-(1-Dc)(1-Dt),对于拉伸损伤Dt和压缩损伤Dc分别定义为
(6)
(7)
(8)

为描述冲击爆炸近区高静水压力特性,Kong-Fang模型采用LS-DYNA软件中的8号状态方程[22]来描述压力和体积应变的关系,通过输入10对压力与体积应变和卸载模量进行线性差值确定。
3.1 破坏面参数
Kong-Fang材料模型中的破坏面参数主要包括:①强度面参数a1,a2,fc,T和模量E等;②损伤参数,压缩损伤参数d1,d2,α和断裂应变εfrac。
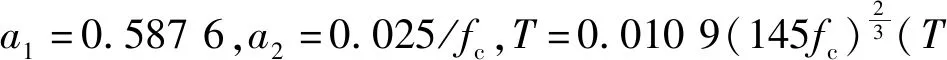
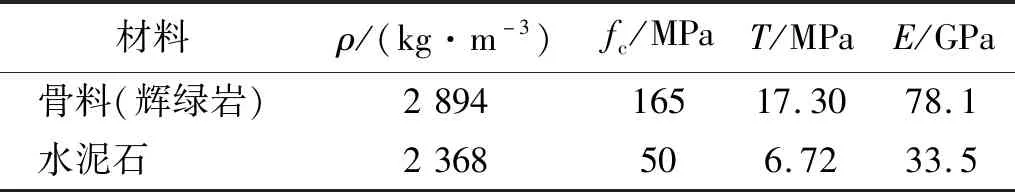
表1 混凝土组分材料部分参数Tab.1 Parameters of concrete components
3.2 状态方程参数
辉绿岩(又称粗玄岩)常用作混凝土中的骨料,基于Tsembelis等平板撞击实验和LASL实验室得到的Hugoniot实验数据,采用分段线性拟合方式,可得到其状态方程,如图5所示。考虑到岩石材料冲击压缩实验数据较为丰富,其他岩石材料可采用相同的方法得到其状态方程。

图5 骨料分段线性高压状态方程Fig.5 Piecewise linear EoS at high pressures of aggregate
水灰比为0.35,水泥石的高压状态方程数据,如图6所示。从图6可知,实验数据存在一定的离散性,采用分段线性拟合方式得到其状态方程。
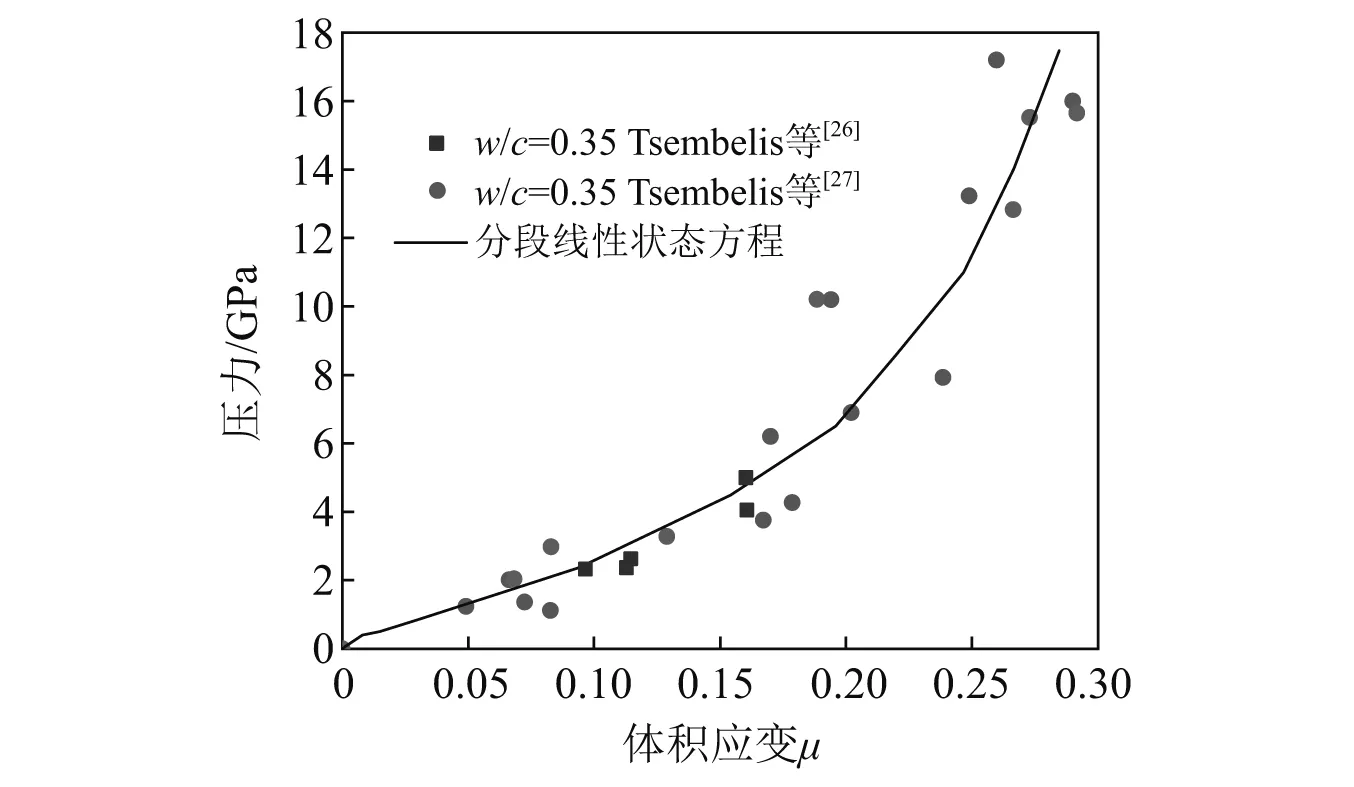
图6 水泥石分段线性高压状态方程Fig.6 Piecewise linear EoS at high pressures of cement stone
水泥石是一种典型的多孔材料,孔隙的坍塌对其高压状态方程有显著影响,而水灰比(w/c)决定了水泥石配合比和孔隙率,因此不同水灰比条件下水泥石的高压状态方程存在明显差异,且已有研究针对水泥石的平板撞击实验数据较少,通过分段线性拟合方法得到其高压状态方程并不实用。
大量实验数据表明,固体中的波速和粒子速度存在明显的线性关系即:Us=cb+sUp,其中:cb为体声速;s为斜率。Riedel等和Gebbeken等分别提出了基于质量和体积分数的Hugoniot混合法,用以确定多相介质的ρ,cb和s。Gebbeken等和Huang等的研究表明,基于体积分数的混合法具有更好的预测性。基于体积混合法则,水泥石的ρ,cb和s可由式(9)确定
H=Σfi·hi
(9)
式中:H和h分别为水泥石和其组分的ρ,cb,s;f为不同组分所占的体积分数;i为水泥石的不同组分。已有研究表明,水泥石中主要存在以下5种组分:未水化水泥、水泥凝胶、凝胶孔隙、毛细孔和气孔,其中凝胶孔隙被凝胶孔水充满,毛细孔被毛细孔水填充[28]。根据德国水泥协会的建议[29],水灰比为0.35的水泥石以上5种组分的体积含量,如表2所示。基于式(9)和表2可得到水灰比为0.35的水泥石ρ,cb和s。

表2 水泥石组分性质及占比Tab.2 Cement stone component properties and proportion
水泥石可采用典型的多项式状态方程,表达式为
P=k1μ+k2μ2+k3μ3
(10)
式中:μ为体积应变;k1,k2和k3可由式(11)~式(13)确定
(11)
(12)
(13)
可得到水灰比为0.35水泥石的状态方程为P=28.02μ+29.97μ2+4.04μ3该状态方程与实验数据的对比,可以看出当体积应变小于0.25时,基于体积混合法则得到的高压状态方程与实验数据吻合较好,而当体积应变大于0.25时,混合法则严重低估了实验数据,如图7所示。
水泥石在孔隙被完全压实后,水泥凝胶的晶体结构会发生变化,因此表2中各组分体积分数及相应的ρ,cb和s也会随之变化,因此Hugoniot混合法则不再适用。注意到水泥石压实密度为2 584 kg/m3(通过混合法则得到),相应的压实应变为μ=ρ/ρ0-1=0.16,见图7,密实段状态方程可经验性地用线性表示,其斜率(体积模量)可拟合为8K0,K0为水泥石的线弹性体积模量,可由基于体积分数的混合法则得到。可以看出经过改进得到的高压状态方程与实验数据较为一致,压力最大误差在7%以内,已有平板撞击实验数据表明,水泥石类材料的密实段体积模量近于8倍的线弹性体积模量,进一步验证了本文经验性取值方法的正确性。
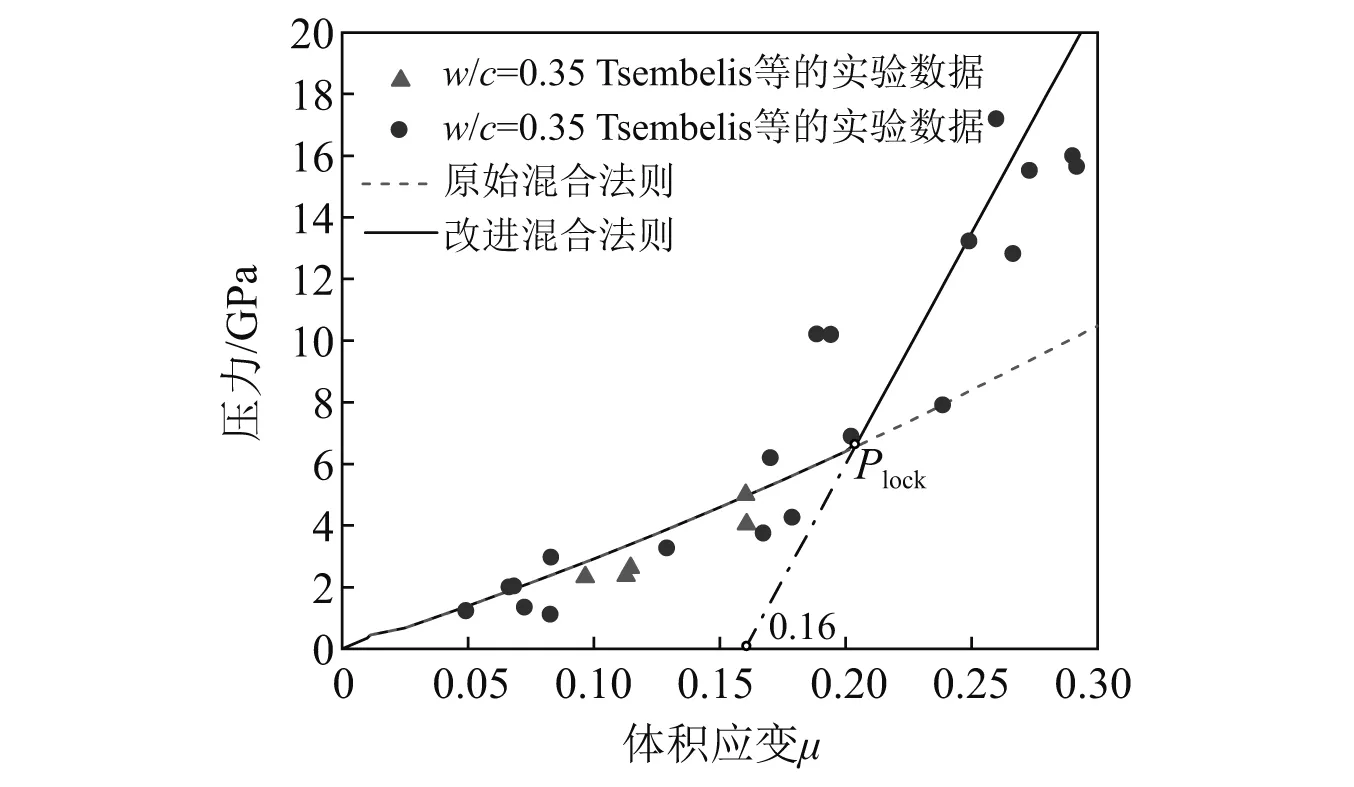
图7 基于原始和改进的体积混合法则预测的高压状态方程与实验数据的对比Fig.7 Comparison of predicted EoS at high pressures by the original and modified volume mixing rule with test data
4 细观模型的预测结果及分析
本章首先基于已有平板撞击实验数据对细观模型进行验证,然后在细观尺度上对冲击波的传播规律进行分析和讨论。
Tsembelis等[30]进行了一组混凝土试件(直径65 mm,厚度20 mm)的平板撞击实验,该实验中混凝土由体积占比45.5%的辉绿岩骨料和54.5%的水泥石(水灰比为0.35)组成,具体级配和用料比等信息,如表3所示。建立与该实验相同骨料体积含量和级配的混凝土细观模型,基于第3章给出的辉绿岩骨料和0.35水灰比水泥石的材料模型,采用第2章给出的方法进行数值模拟,可得到该混凝土试件的高压状态方程。数值模拟得到的高压状态方程与实验数据的对比,如图8所示。由图8可知:数值预测结果与实验数据非常接近,验证了基于细观模型和改进的混合法则确定混凝土高压状态方程的正确性。

表3 混凝土组分占比Tab.3 The proportion of concrete components
由图8可知:混凝土材料的Hugoniot弹性极限PHEL为0.4 GPa,这与Hall等、Grady和Gebbeken等利用平板撞击实验得到的结果相近。
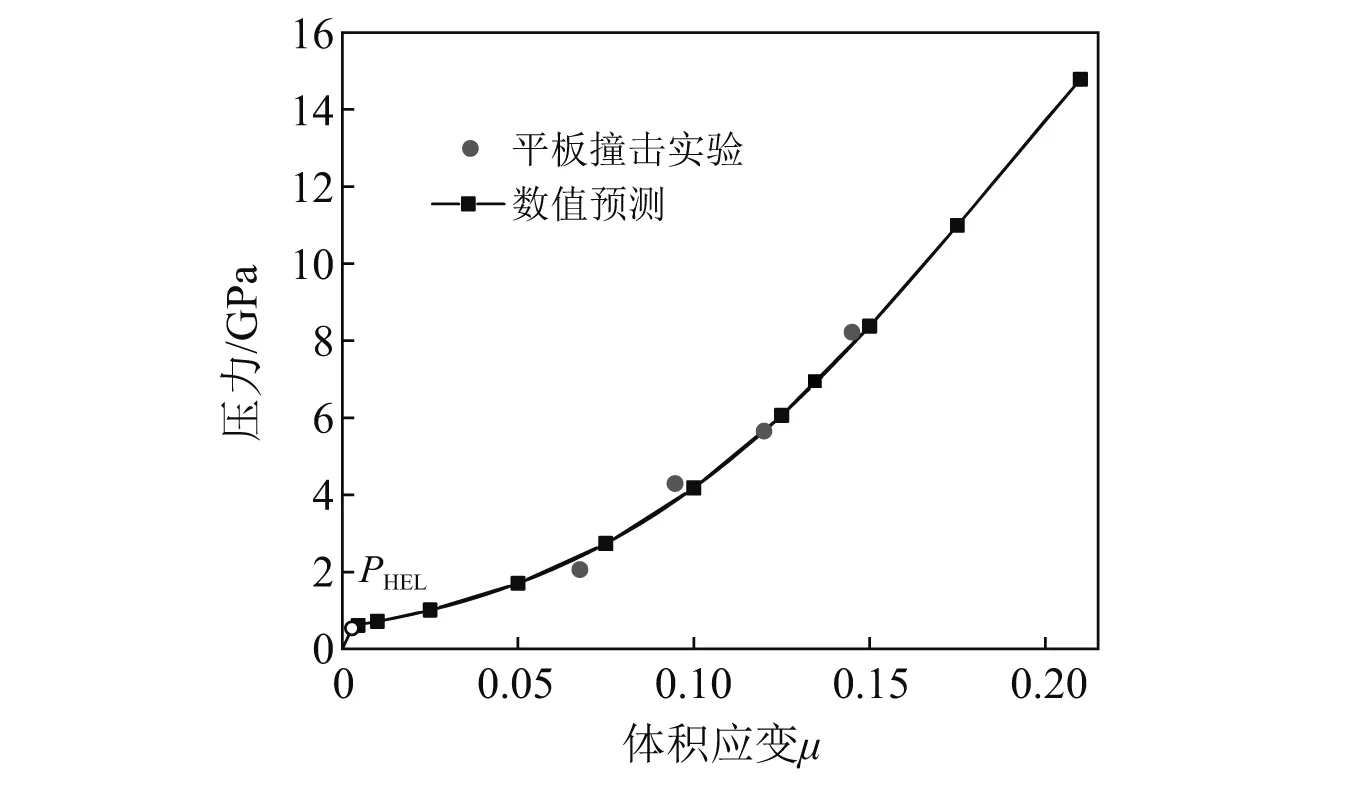
图8 基于细观模型预测的高压状态方程与实验数据的对比Fig.8 Comparison of numerically predicted EoS at high pressures with test data
图9(a)给出了当粒子加载速度为500 m/s时,X轴方向50 mm,75 mm和125 mm 3个截面典型单元的压力时程曲线,可以看出明显的弹性前驱波平台(约为0.4 GPa)、压力升时段和塑性波平台,压力时程曲线的上下波动(在已有平板撞击实验中同样发现)是由于骨料和水泥石波阻抗不同造成的复杂反射引起的。
图9(b)给出了该工况下25 μs时的压力分布云图,可以看出明显的锯齿状压力分界线A-A,B-B和C-C(对应于图9(a)的3个阶段),锯齿状是由混凝土材料的非均质性引起的。

图9 细观水平压力分布Fig.9 Pressure distribution on mesoscopic level
5 参数敏感性分析
在计算流体动力学软件中,材料行为对于偏量和球量分别处理,注意到在一维应变状态下,应力偏量和球量同时存在,因此第3章基于细观模型确定混凝土高压状态方程的方法中基本假定为偏量不会对球量产生较大影响,本章对破坏面参数进行敏感性分析验证该假设的正确性。骨料体积含量及形状的影响已在作者前期工作中进行了细致探讨,这里不再赘述。考虑到水灰比对水泥石的性能影响较大,因此本章进一步研究水灰比对混凝土高压状态方程的影响并进行了单参数敏感性分析。
5.1 破坏面参数
为探讨应力偏量(用破坏面描述)对混凝土高压状态方程的影响,本节首先对Kong-Fang模型中的强度面参数进行单参数敏感性分析(同时变化骨料和水泥石参数如a1),即仅变化所讨论参数(按±10%和±20%幅度变化)而保持其他参数不变。
Kong-Fang模型中最大强度面和残余强度面大小由参数a1和a2控制,a1和a2对混凝土高压状态方程的影响,如图10所示。由图10可知:在讨论的参数变化范围内(±20%内),a1和a2对高压状态方程几乎没有影响。
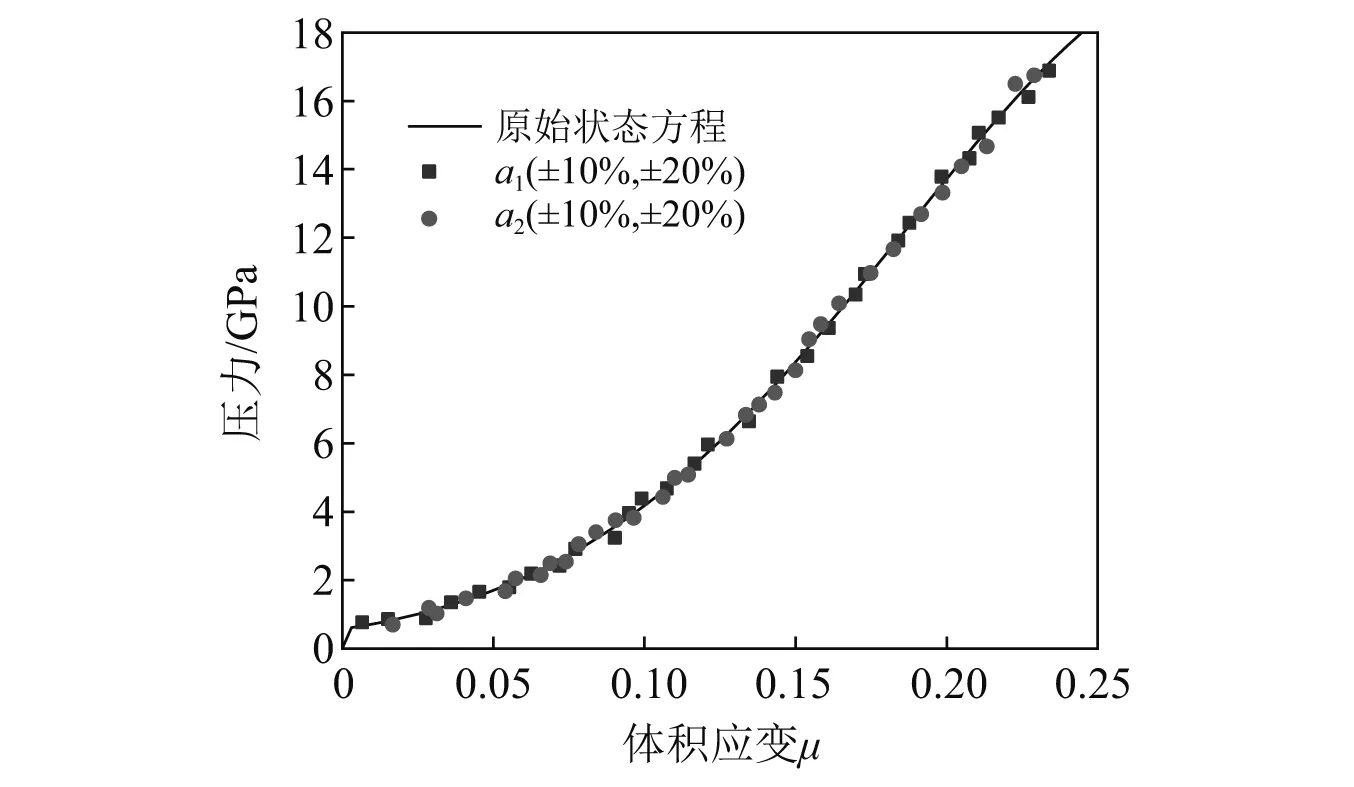
图10 强度面参数敏感性分析Fig.10 Sensitivity analysis of strength surface parameters
Kong-Fang模型中损伤参数影响到压缩和拉伸损伤累积的快慢,包括压缩损伤参数d1,d2,α和拉伸损伤参数εfrac,损伤参数对高压状态方程的影响,如图11所示。可以看出影响较小可以忽略。

图11 损伤参数敏感性分析Fig.11 Sensitivity analysis of damage-related parameters
通过本章敏感性分析可得出,材料模型中的破坏面(即偏量部分)对高压状态方程的影响有限,因此在一维平面应变的高压力状态中偏量和球量可近似解耦,且在缺少实验数据情况下细观模型中骨料和水泥石的破坏面可不必精确确定,采用Kong-Fang模型中自动生成的参数即可满足要求。
5.2 水灰比
由第3章可知,水泥石的组分配合比和孔隙率由水灰比决定,调整水灰比会同时改变水泥石的破坏面和状态方程,本节考虑另一典型水灰比0.56,参考已有实验数据[31],该水灰比下的水泥石fc=35 MPa和E=30.7 GPa,其他强度面参数按照Kong-Fang模型自动生成得到。该水灰比下水泥石组分配合比可根据德国水泥协会的建议得到,进而基于本文提出的改进的混合法则得到其高压状态方程。
在相同的骨料级配下,基于细观模型得到的两种水灰比下的混凝土高压状态方程,如图12所示。由图12可知:水灰比对混凝土高压状态方程的影响非常明显,随着水灰比减小,水化作用产生的毛细孔数量大幅减少,水泥石中凝胶产物占比变大,混凝土组分间粘结力增强,混凝土材料的加载体积模量增大,即在相同体积应变下压力更高。初始粒子速度800 m/s工况下t=17 μs时刻的压力云图,如图13所示。由图13可知:冲击波在低水灰比下传播更快,进一步说明了其加载体积模量更高。
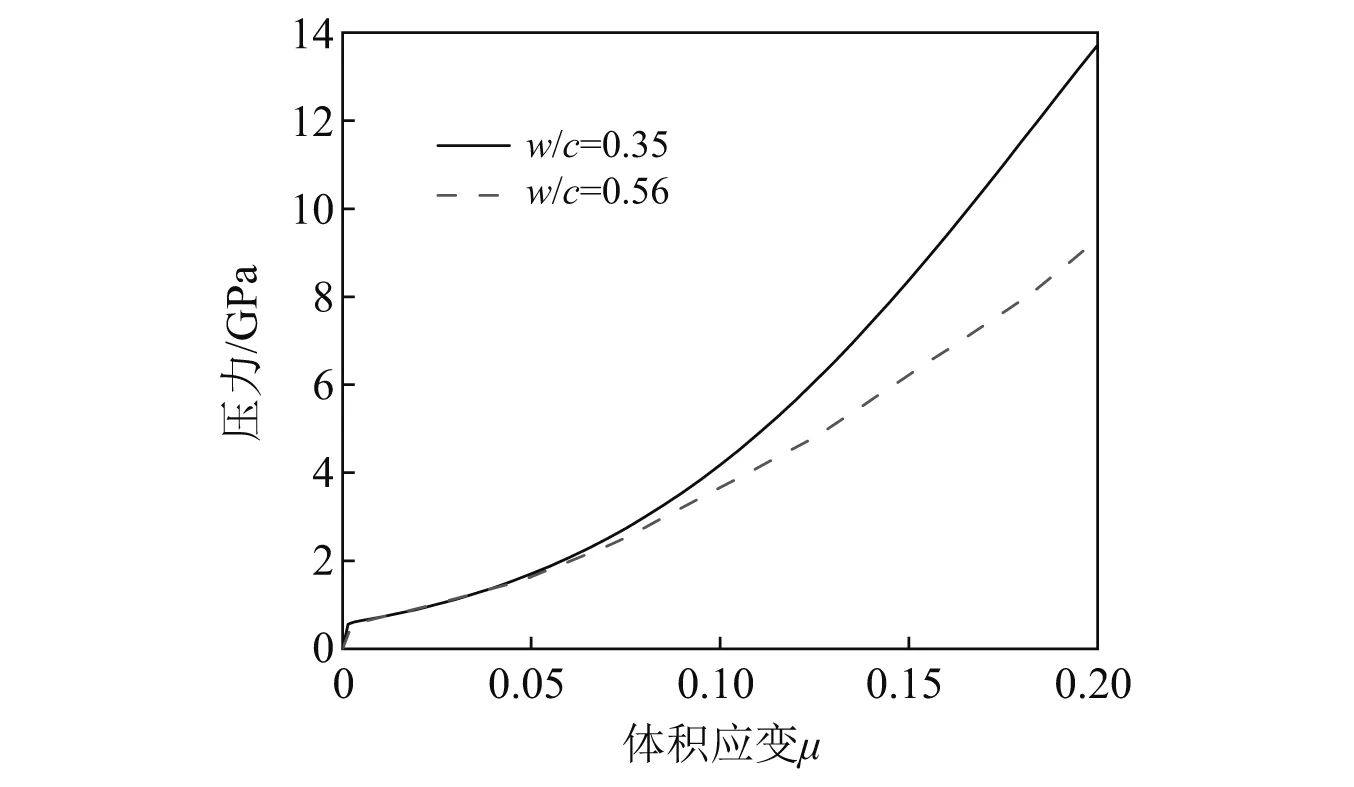
图12 不同水灰比混凝土高压状态方程Fig.12 EoS of concrete with different water-cement ratio
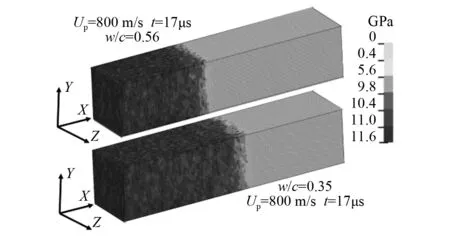
图13 不同水灰比压力云图Fig.13 Pressure contour of different water-cement ratio
6 结 论
基于作者前期提出的混凝土两相介质细观模型和混凝土类材料的Kong-Fang材料模型,本文在细观尺度上对混凝土高压状态方程的确定、基于体积分数的混合法则、冲击波在两相介质细观尺度上的传播规律以及强度面和水灰比敏感性等方面进行了详细探讨,主要研究工作和结论如下:
(1)提出了一种改进的基于体积分数的混合法则确定水泥石的高压状态方程,在压实阶段,仍采用原有体积分数混合法则;而在密实段,由于水泥凝胶晶体结构发生变化等因素,原有混合法则不再适用,基于已有实验数据可得到了密实段的加载模量。
(2)在细观尺度上分析了混凝土中冲击波传播规律,发现数值模拟和已有实验中测得的压力波动现象是由混凝土材料的非均质性造成的。
(3)参数敏感性分析结果表明,用于描述混凝土偏量的破坏面参数对高压状态方程影响较小,在一维平面应变的高压力状态中偏量和球量可近似解耦,因此在基于该方法确定混凝土高压状态方程时,破坏面可不必精确确定,极大简化了模型参数标定的复杂度。而水灰比决定了水泥石的组分配合比和孔隙率,对高压状态方程影响较大,因此采用该方法时需明确混凝土的水灰比。
(4)通过细致了解混凝土中骨料和水泥石一维平面应变高压力下的球量关系,可将本文基于细观模型确定混凝土高压状态方程的方法推广至任意配合比混凝土,数值模拟结果得到了已有平板撞击实验数据的较好验证。
