基于灰箱模型的垂向车-桥系统响应极值分布研究
2021-09-27李永乐向活跃
唐 平,李永乐,向活跃
(西南交通大学 土木工程学院,成都 610031)
随着我国轨道交通建设的快速发展,高速列车以高速舒适的优势在全国范围内得到大规模地建设。在我国高铁大发展的同时,在营高铁的可靠性也越来越多地被研究。由于车-桥系统相对复杂的非线性和轨道激励的随机性,使得这一研究遇到很多障碍。
随着随机振动理论的发展和成熟,学者们提出了很多随机性方法,并被应用到了车-桥耦合振动中,如协方差分析法[1]、演变随机响应法[2-3]以及虚拟激励法[4-7]等,但当对象为非线性系统或需要计算小概率失效事件时,以上方法还有很多缺陷。除了上述随机振动方法,最直观通用的还是Monte Carlo模拟(Monte Carlo simulation,MCS),此模拟方法不受系统线性或非线性影响,但得到的结果变异系数与模拟次数的开方成反比,在失效概率很小时,需要的样本数目很大。因此,提高每个样本计算效率或减少样本数目是非常必要的。在减少非线性结构小失效概率动力可靠性计算所需MCS样本量方面,比较有效的是子集模拟以及在其框架上衍生的一些方法[8-11],其本质还是基于条件概率的MCS。
而在提高样本计算效率方面,有学者提出桥梁代理模型[12];对于垂向车-桥系统,也有学者采用非线性神经网络模型[13];还有学者针对轮轨几何接触点的计算[14]、轮轨力的预测[15]提出过一系列人工神经网络模型。以上方法都将重心放在简化车-桥模型的某个点上,使用各类代理模型简化计算。大部分代理模型虽然能在一定程度上提高计算效率,但由于未对计算框架进行简化,效率提高有限。
本文针对垂向车-桥系统,采用车辆结构的灰箱模型进行参数优化,根据无轨道不平顺时近似轮轨力作为车辆灰箱模型输入,以及考虑轮轨不平顺时原始车-桥系统车辆响应作为输出,对车辆结构灰箱模型参数进行最佳拟合,提出一种高效且高精度的计算框架。由于车辆结构已知,考虑到MATLAB软件的系统辨识工具箱中灰箱辨识模型能够方便地建立车辆结构模型,并进行参数优化,为了方便高效,本工作采用了MATLAB软件中的灰箱模型来进行车辆参数优化。
1 垂向车-桥系统耦合模型
1.1 车辆模型
车辆模型采用CRH型动车,8车编组,每辆车包括一个车体,两个转向架,分别考虑其沉浮与点头自由度,则整个车辆模型为6自由度动力系统,车辆垂向系统模型如图1所示[16]。

图1 列车的质量弹簧阻尼模型Fig.1 Mass-spring-damping model of the train
轮轨作用力简化为直接作用于转向架的外荷载,此作用力的表达式为:
竖向荷载
(1)
转动荷载
(2)
式中:j为转向架号;i为轮对号;Kp,Cp为一系悬挂刚度和阻尼;lw为同一转向架两轮对距离之半。
根据达朗贝尔原理,可以列出6个自由度上的运动方程,其具体表达式可以参考毛云霄等的研究,最终组集成矩阵形式表达为
(3)
式中:Mv,Cv,Kv分别为车辆的质量、阻尼、刚度矩阵;Fv为外荷载,其表达式为Fv=[0 0Fbz1Fbφ1Fbz2Fbφ2]T;uv为车辆位移。
1.2 桥梁模型
桥梁采用高铁中广泛使用的高架简支梁桥,桥梁每跨长32 m,共50跨1 600 m。墩高10 m,桥宽12 m,高3.05 m,桥梁截面如图2所示。

图2 桥梁横截面图(mm)Fig.2 Bridge cross-section (mm)
桥梁采用商业有限元软件ANSYS建模,并导出桥梁有限元模型的质量与刚度矩阵,再结合桥梁的第一阶竖弯与第一阶扭转频率,采用瑞利阻尼计算公式求得桥梁模型阻尼矩阵。外荷载矩阵需要根据车辆轮对不同时刻位于桥梁各单元的位置以及作用力大小,进行桥梁单元内插值计算,转换为所在桥梁单元的节点荷载。最终,桥梁模型的运动方程可以采用矩阵形式表达为
(4)
式中:Mb,Cb,Kb分别为桥梁的质量、阻尼、刚度矩阵;Fb为外荷载矢量,其合力与作用在车辆转向架上的力等大反向。
2 轨道不平顺的模拟
由于本工作侧重于提出近似的计算方法,而轨道不平顺的选取对方法的说明并无影响。本工作中轨道不平顺采用德国高速垂向低干扰谱,其表达式为
(5)
式中:Ω为空间频率,rad/m;Av=4.032×10-7rad·m;Ωc=0.824 6 rad/m;Ωr=0.020 6 rad/m。
轨道不平顺的模拟采用白噪声滤波法,其主要做法是根据需要模拟的功率谱的特点,设计相应的滤波器,将白噪声作为输入,输出与所需模拟的功率谱相吻合的随机样本。由于德国低干谱给出的是空间域功率谱函数,需要将其转化为时间域功率密度谱,式(5)转化为时间域功率密度谱后表达式为
(6)
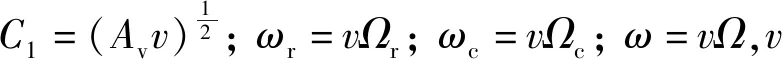
根据文献[17],可以推导出所需白噪声滤波器的微分方程为
(7)
(8)
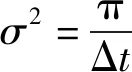
对于式(7)和式(8)所示的线性时不变系统,写成矩阵形式为
(9)
(10)
由式(9)和式(10),得到此线性时不变系统的A,B,C,D4个矩阵。即

(11)
此时,只要输入白噪声序列r1,即可通过式(9)和式(10)得到轨道不平顺时程y。通过这种方法得到的轨道不平顺包含了所有的频率成分,需要再次滤波,去除不需要的低频和高频部分。文献[18]表明,在轨道不平顺激励作用下,车体和轮对的垂向、横向振动加速度主要频率范围为1~3 Hz和3~120 Hz。本工作中取0.4~80.0 m的波长段,并将不属于此波长段对应频率的频率成分滤除。通过滤波后得到的轨道垂向不平顺样本以及样本功率谱与理论谱的对比,如图3所示。从图3可知:通过白噪声滤波法生成并通过滤波后的轨道不平顺样本功率谱与理论谱吻合较好,验证了生成的轨道不平顺样本的正确性。
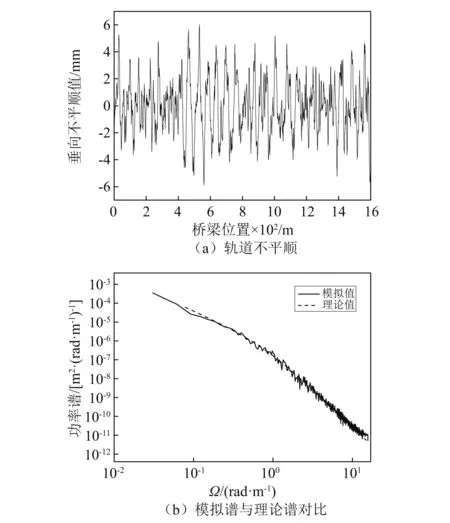
图3 轨道不平顺模拟Fig.3 Simulation of track irregularity
3 车辆灰箱代理模型
3.1 灰箱模型理论
灰箱系统辨识作为系统识别的一种方法,与黑箱系统辨识不同,此辨识方法需要事先了解系统的结构,但是对于其结构参数值不清楚,根据系统输入和输出,采用最小化误差的原则,对结构的参数进行最佳估值[19]。
建立灰箱系统辨识模型时,需要将系统的运动微分方程改写成状态方程,并定义状态初值,状态方程具有以下形式

(12)
式中:A,B,C,D为由各个系统参数参数化表示的矩阵;K为噪声矩阵,Ke(t)可以为由系统参数参数化表示的标量;x0为状态初值向量。
在灰箱辨识模型结构建立之后,以定义的系统参数值初值开始,采用子空间Gauss-Newton最小二乘搜索,Levenberg-Marquardt最小二乘搜索,自适应的子空间Gauss-Newton最小二乘搜索,最速下降法等优化算法[20],迭代估计系统参数值,以将模型估计的输出值与需要辨识的输出值的误差最小化。
3.2 轨道不平顺对桥梁和车辆响应影响
由于高铁桥梁主梁刚度都比较大,因此,桥梁变形主要来自于车辆重力,轨道不平顺导致的轮轨力对桥梁变形影响不大。在此,分别计算了8车编组动车过桥时,有轨道不平顺作用及无轨道不平顺作用下,第一辆车第一个轮对处的桥梁响应,如图4所示。从图4可知:有轨道不平顺作用时,桥梁的位移和速度与无轨道不平顺作用时大体吻合,只有局部地方有很小的波动。而这些桥梁位移和速度小波动将影响车辆加速度。
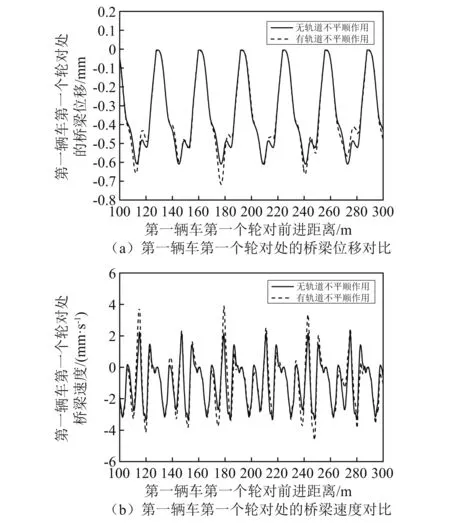
图4 第一辆车第一个轮对处的桥梁响应对比Fig.4 Comparison of bridge displacement and velocity at the front wheel of the first vehicle
为了探究桥梁位移与速度差异对于车辆加速度响应的影响。定义两种计算方式为方式①和方式②:方式①为直接以无轨道不平顺时桥梁位移叠加轨道不平顺,再计算输入车辆系统作用力,最后求解车辆方程的车体响应;方式②为直接解车桥运动方程得到车体响应。分别采用随机生成的400不平顺样本按方式①和方式②计算。400个样本中第一辆车车体加速度最大值结果与相同轨道不平顺作用下直接解车桥运动方程的结果比较,如图5所示。
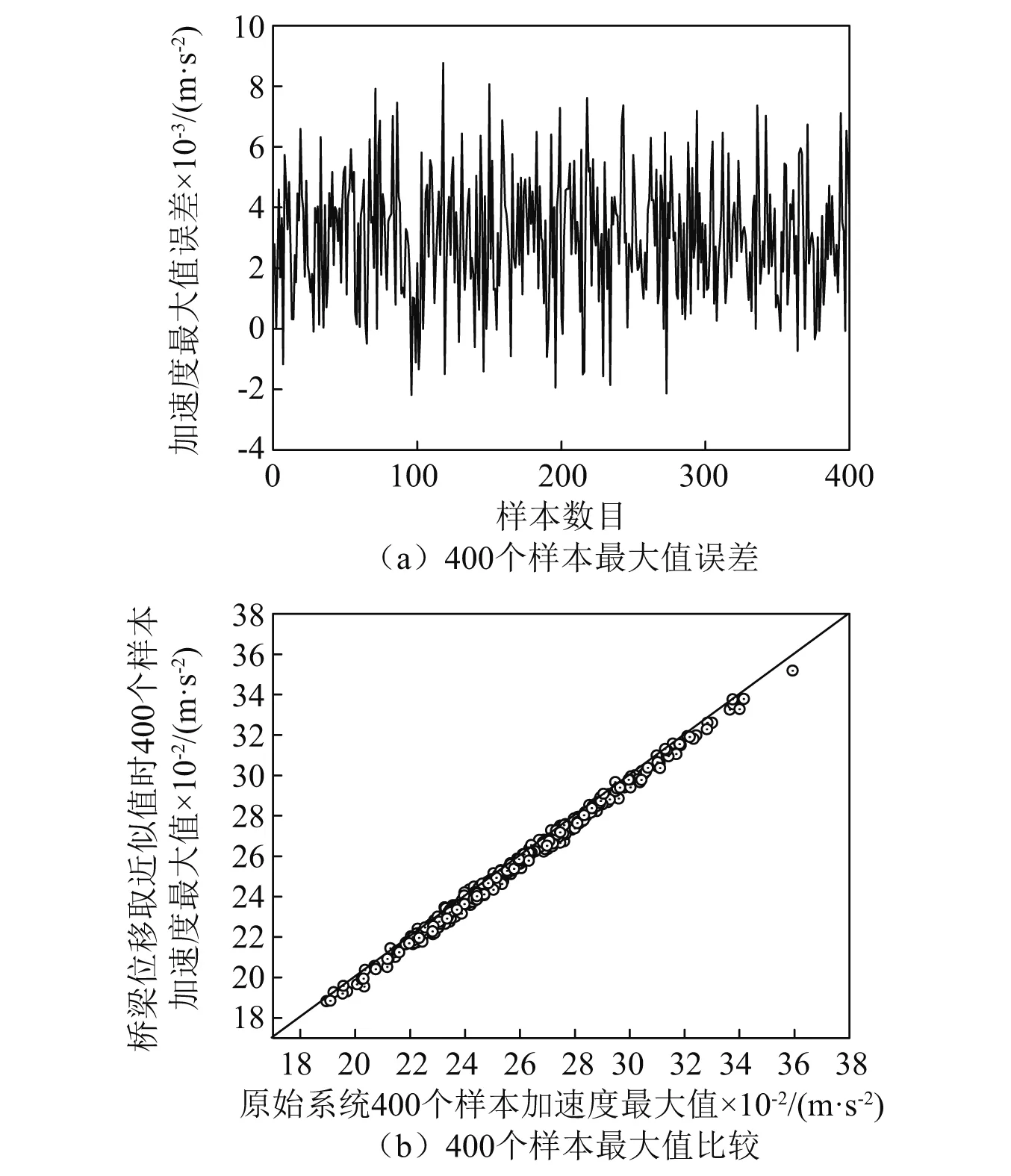
图5 400个样本车体加速度最大值比较Fig.5 Comparison of vehicle maximum acceleration of 400 sample
由图5可知,直接以无轨道不平顺时桥梁变形作为有轨道不平顺作用下桥梁变形值时(方式①),计算得到的车体加速值总体偏小。因此,如果能将此误差均值尽量缩小,就能在计算车辆加速度响应时,直接采用无轨道不平顺时桥梁变形值作为有轨道不平顺作用下桥梁变形值。这样做的好处在于,可以在无轨道不平顺条件下,计算桥梁变形时程,只需计算一次桥梁变形。这样,就可以确定每个时步各轮对处桥梁位移,这部分也只需要计算一次。在考虑轨道不平顺后,直接在此基础上叠加轨道不平顺。而求解原始车桥运动方程时(方式②),每个样本每一时步都要计算桥梁位移值,并且都要进行插值计算各轮对处桥梁位移。因此,如果能直接采用无轨道不平顺时桥梁变形值作为有轨道不平顺作用下桥梁变形值,当求解多个样本时,整个计算时间将会大大减少。
3.3 车辆灰箱模型建立流程
对于垂向车桥系统,本应是参数确定系统,但由于要将桥梁位移近似,为了使此近似对车辆响应影响最小,可以细微调整车辆参数。而灰箱系统辨识可以很好实现这个目标。在进行车辆系统灰箱系统辨识时,按方式①计算得到作用在转向架上的力,以此作为车辆灰箱系统的输入。再将相同轨道不平顺作用下,求解原始车桥运动方程(方式②)得到的车辆响应作为系统输出值,根据此输入输出,对车辆参数进行辨识。
为了灰箱模型建立与辨识的高效可靠,本工作采用了MATLAB软件中系统辨识工具箱里的灰箱系统辨识组件。建立车辆灰箱系统辨识模型时,由于垂向车桥系统的车辆模型考虑6个自由度,因此,状态量一共选取了12个,即6个自由度方向的位移与速度,并将式(3)改写成状态方程。并将车辆状态方程编写为C MEX文件,以导入MATLAB软件生成车辆灰箱模型。在进行灰箱模型参数优化时,本工作采用的是MATLAB软件内置的Levenberg-Marquardt最小二乘搜索算法。
在进行灰箱系统识别时,代表样本的选择值得一提。根据图5所示的计算结果,方式①计算得到的车体加速度响应最大值普遍偏小。因此,优化车辆参数的目的是将此种方式计算的响应最大值整体增大。要使所有样本的最大值误差均值接近0,则应该选择中间误差的样本作为代表样本。为此,在选择代表样本时,可以先采用100个样本,按方式①和方式②分别计算车体加速度最大值。并将误差按大小排列,取中间误差样本作为代表样本。
在得到代表样本后,按方式①计算作用在车辆转向架上的力,作为灰箱辨识系统的输入,按方式②计算得到的车体相应作为输出,进行系统参数识别。部分参数识别前后变化,如表1所示。由1表可知:车辆参数在辨识前后有了细微调整,从而使得优化后的车辆模型能最小化近似计算的误差。系统辨识结果如图6所示。由6图可知:车体加速度相应的模拟值与原始动力方程求解值吻合很好,这也验证了建立的灰箱系统辨识模型正确性。

表1 车辆部分参数识别前后比较Tab.1 Comparison of partial vehicle parameters before and after identification

图6 灰箱辨识模型模拟值与直接求解运动方程结果比较Fig.6 Comparison between simulated values of grey-box identification model and solution of motion equation
在得到车辆灰箱系统后,便可使用其进行垂向车桥系统车辆动力响应计算。
4 计算流程
在车辆的灰箱辨识模型参数优化后,便可利用其计算车辆的加速度响应。计算步骤总结如下:
步骤1在无轨道不平顺作用下,计算桥梁位移与速度时程;
步骤2根据步骤1中的桥梁位移与速度时程,插值计算每个时步车辆各轮对处桥梁位移与速度值;
步骤3白噪声滤波法生成轨道不平顺时程,并叠加步骤2中的桥梁位移与速度,得到车辆各轮对处的等效不平顺时程,并计算作用在车辆转向架上的力;
步骤4将步骤3中得到的力时程输入车辆系统的灰箱模型,得到车辆的响应值。
5 结果分析
按照第4章的计算流程,计算了1 200个样本(包括图5中400个样本的轨道不平顺)的第一辆车车体加速度响应最大值。此最大值与根据原始的车桥运动方程计算得到的最大值比较,如图7所示。由图7可知:图5中的400条不平顺样本结果总体偏小的趋势已被明显改善,额外的800条随机样本下的结果也与原始系统计算值吻合很好,最大误差不超过5%,并且,误差均值接近0。在相同计算设备条件(计算机处理器:Intel(R)Core(TM)i5-3210M CPU @2.50 GHz 2.5 GHz,内存:8 GB)下,求解原始车桥运动方程共用时106 670 s,而基于灰箱辨识模型计算方法共用时15 707 s,用时仅为前者的1/7左右,大大提高了求解车辆响应的效率。
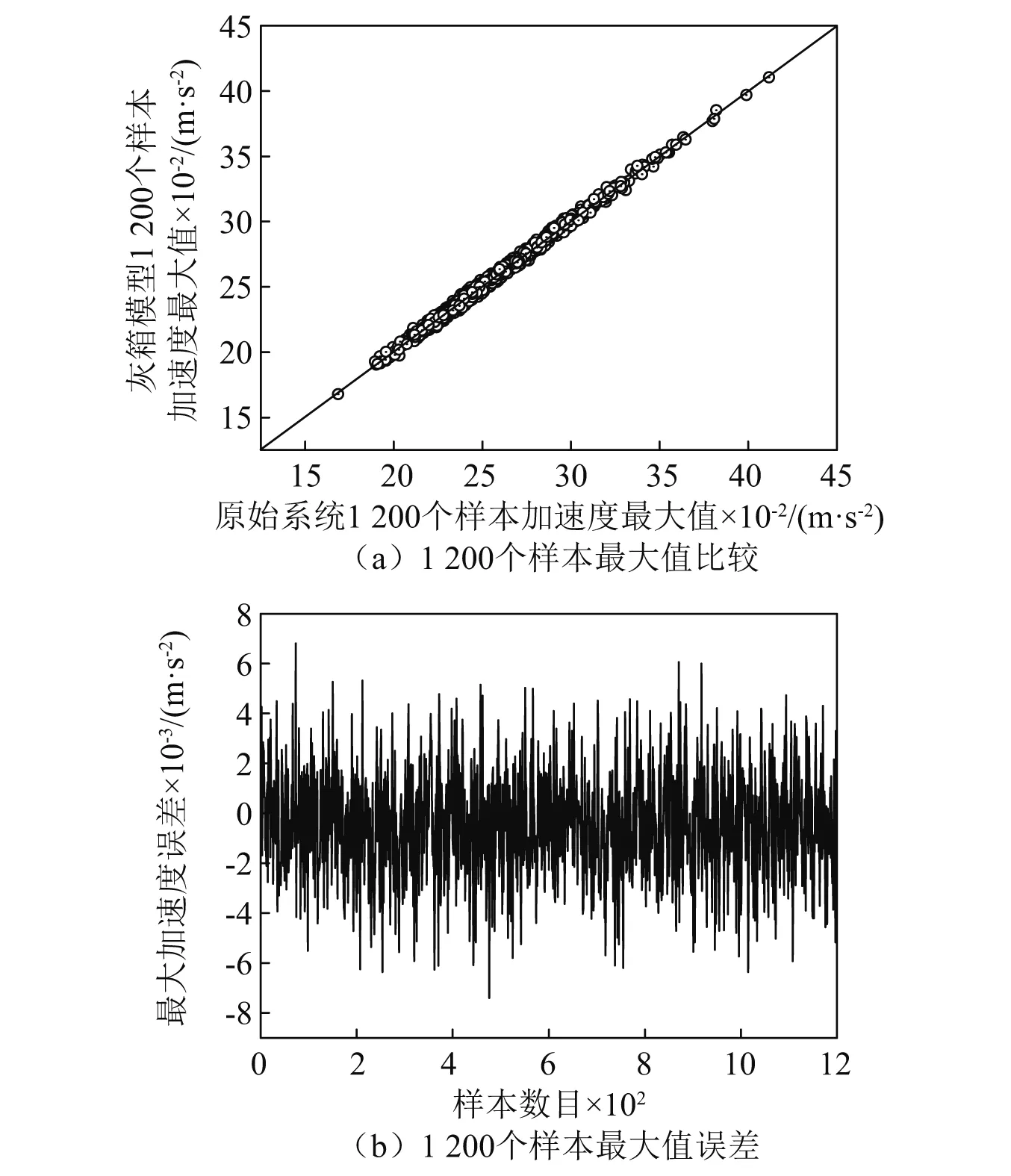
图7 1 200个样本车体加速度最大值比较Fig.7 Comparison of vehicle maximum acceleration of 1 200 sample
根据此1 200个样本计算结果,对车体加速度响应极值分布进行了研究,使用本文框架计算的极值分布图与原始车-桥方程计算的极值分布,如图8所示。由图8可知:本文所提方法得到的响应极值分布与求解原始车-桥运动方程得到的极值分布吻合很好,验证了使用本文所提方法研究垂向车-桥系统响应极值分布的可行性。

图8 1 200个样本车体加速度最大值分布比较Fig.8 Comparison of vehicle maximum acceleration distribution of 1 200 sample
6 结 论
本文所提的基于灰箱系统计算车体动力响应的方法,利用桥梁的近似响应时程,结合车辆灰箱辨识模型,简化了垂向车-桥系统中计算车辆动力响应的过程,并使用1 200个样本验证了其高效性与准确性。结果表明:车辆灰箱模型计算误差较小,相同样本量的计算用时较少,为求解原始车-桥运动方程的1/7左右,且车体加速度响应极值分布曲线与求解系统原始运动方程结果吻合很好。这对于小概率事件进行模拟时能够凸显出其高效的优势。
