新型轴向磁气组合轴承性能研究

陈李成，谢振宇，吴 炎，郝建胜

(南京航空航天大学 直升机传动技术重点实验室，南京 210016)

磁轴承和气体轴承是机械支承的两个重要发展方向，都有转速高、节能、环保等特点，但是磁轴承需要辅助的保护轴承[1-2]，动压气体轴承在低转速状态下会产生接触摩擦，因此将两者组合使用可以弥补各自的缺点：一是低转速状态下，磁轴承为转子提供支承力，防止气体轴承与转子产生接触摩擦；二是在高转速状态下，气体轴承可以提供一定的附加支承力，有利于提高系统的动态性能；三是在磁轴承失效时，气体轴承可以作为保护轴承，减轻转子直接撞击造成的损害。因此，磁气组合轴承是高速旋转机械的一种理想支承方式。

由于磁气组合轴承独特的优越性，近年来对此类轴承的研究也越来越多，目前多数研究的还是基于箔片动压气体轴承或者是静压气体轴承的磁气组合轴承。Swanson等[3]研究了应用于燃气轮机的箔-磁组合轴承，建立了小型燃气轮机转子动力学模拟试验台，证实了箔片动压气体轴承作为保护轴承的可能性。Pham等[4]研究了箔片动压气体轴承与主动磁轴承相结合的箔-磁组合轴承，并建立了箔-磁组合轴承支承的柔性转子试验台，该研究证实了磁气组合轴承有刚度大，并且节能的优点。樊登柱等[5]研究了箔-磁组合轴承，并将此组合轴承应用于高速永磁同步电动机，有限元分析结果表明，轴承-转子系统能够安全升速到额定转速。李媛媛[6]将混合箔-磁轴承应用于透平膨胀机，试验结果表明，转子在升速过程和突然增加载荷的作用下，不会产生较大的振动，组合轴承的支承性能明显提高。

目前，国内外对于基于螺旋槽型动压气体止推轴承(spiral groove gas bearing，SGGB)[7]的磁气组合轴承研究比较少。解志杰[8]研究了螺旋槽型动压气体止推轴承与永磁轴承相结合的轴向磁气组合轴承，通过搭建磁气组合轴承试验台，验证了在12 000 r/min的转速下磁气组合轴承的承载力达到了126 N，其中气体轴承承载力的理论计算值为21 N，试验测试值为3 N。该研究为以螺旋槽型动压气体止推轴承作为部件的轴向磁气组合轴承的可实施性进行了初步验证，但由于转速较低和气膜间隙较大等原因，气体轴承提供的承载力较小[9]。

与以上研究相比，本文将螺旋槽型动压气体止推轴承与主动磁轴承[10]相结合，通过仿真分析和试验，研究了轴向磁气组合轴承的相关性能。研究结果表明，引入螺旋槽型动压气体止推轴承，有助于提高系统的动态性能，当轴向磁轴承失效时，气体轴承可以起到保护轴承的作用，减轻转子直接撞击造成的损害。

1 轴向磁气组合轴承试验台与数学模型

轴向磁气组合轴承框图，如图1所示，其工作原理简述为：当转子偏离轴向平衡位置时，传感器检测到转子的轴向位置，控制器将位置信号与参考信号进行比较，并根据差值产生控制信号，功率放大器根据控制信号实时改变轴向磁轴承线圈中的电流大小，从而使转子回到平衡位置；同时，当转子达到一定转速后，动压气体止推轴承将产生额外支承力，对转子产生辅助支承作用；另外，当轴向磁轴承失效时，动压气体止推轴承还可以作为保护轴承，减小转子直接碰撞造成的损害。

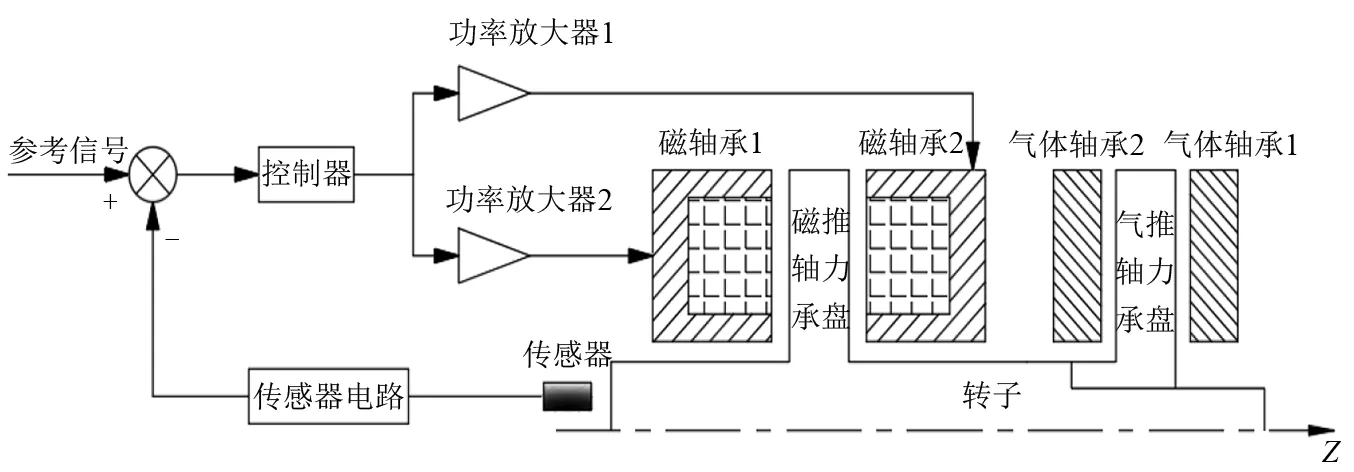
图1 轴向磁气组合轴承框图Fig.1 Block diagram of axial magnetic-gas bearing

1.1 轴向磁气组合轴承试验台设计

轴向磁气组合轴承试验台机械结构图，如图2所示。试验台实物图，如图3所示。

1.左径向传感器；2.左径向磁轴承；3.电机；4.转子；5.轴向磁轴承；6.右径向磁轴承；7.右径向传感器；8.螺旋槽型动压气体止推轴承；9.轴向传感器。图2 磁气组合轴承试验台机械结构图Fig.2 Mechanical structure diagram of magnetic-gas bearing test bench

1.变频器；2.图2所示的机械结构；3.电源箱；4.电控箱。图3 磁气组合轴承试验台实物图Fig.3 Diagram of magnetic-gas bearing test bed

1.2 轴向磁气组合轴承转子系统数学模型

1.2.1 轴向磁轴承电磁力分析

单边轴向磁轴承的电磁力是气隙与线圈电流的函数[11]，可写为

(1)

将式(1)在点i=i0,z=z0的邻域内按照二元函数的泰勒级数展开可得

F(i,z)=F(i0,z0)+ki(i-i0)-kz(z-z0)

(2)

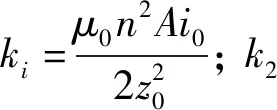
在本文中，轴向磁轴承偏置电流i0的设计值为2 A，轴向磁轴承单边气隙z0的设计值为0.25 mm，故可得电流刚度ki=45.37 N/A，位移刚度k2=362.94 N/mm。

采用差动控制策略的轴向磁气组合轴承转子受力分析图，如图4所示。当转子向Z轴负方向偏移一定位移z后，为了将转子拉回平衡位置，磁轴承1的线圈电流减小iz，同时磁轴承2的线圈电流将增加iz。由式(2)得

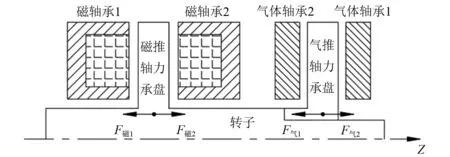
图4 轴向磁气组合轴承转子受力分析图Fig.4 Schematic diagram of force to the rotor of axial magnetic-gas bearing

F磁1=F(z0,i0)+ki(i0-iz-i0)-kz(z0-z-z0)

(3)

F磁2=F(z0,i0)+ki(i0+iz-i0)-kz(z0+z-z0)

(4)

则轴向磁轴承的电磁力F磁可表示为

F磁=F磁2-F磁1=2kiiz-2kzz

(5)

1.2.2 轴向组合轴承转子系统数学模型的建立

如图4所示，气体轴承的承载力可表示为：F气=F气2-F气1，根据牛顿第二定律可推得

(6)

式(6)即为轴向磁气组合轴承转子系统的数学模型，其中本文的转子质量m的设计值为6 kg。

本文为了研究气体轴承在轴向磁气组合轴承中所起的作用，将气体轴承2加工成光面，使得气体轴承2不产生承载力。当转子推力盘从中心位置靠近气体轴承1时，气体轴承1产生的力F气1沿Z轴负方向；当转子推力盘从中心位置远离气体轴承1时，气体轴承1的力逐渐减小，直至为0。此时磁气组合轴承的数学模型可以写为

(7)

对式(7)进行拉普拉斯变换得

(8)

2 螺旋槽型动压气体止推轴承的优化设计

2.1 气体轴承的承载力仿真

螺旋槽型动压气体止推轴承[12]，如图5所示。图5中：α为流入角；β为螺旋角；Ri为轴承内半径；Ro为轴承外半径；Rg为槽端半径；b1为凸台占比角度；b2为槽的占比角度；另外还有一个参数槽深h未在图5中表示。

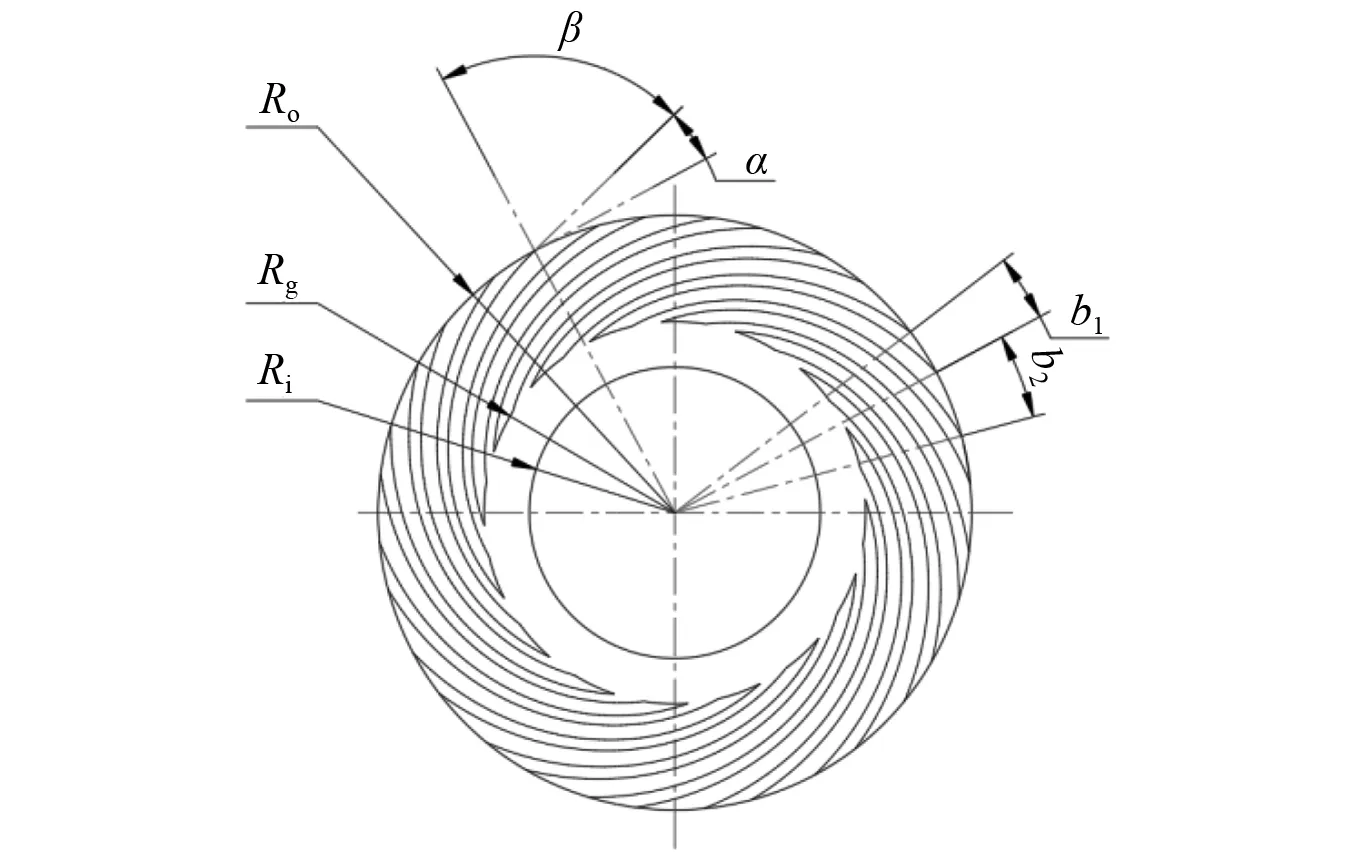
图5 螺旋槽型动压气体止推轴承Fig.5 The spiral groove gas bearing

在对气体轴承优化设计之前，首要研究的是气体轴承承载力仿真问题。前人多采用普惠尔不可压缩理论、准不可压缩窄槽理论、缪德曼不可压缩理论、局部可压缩理论、数值分析法等对气体轴承进行研究。由于计算机的快速发展，本文采用的是Fluent流体仿真软件[13]对气体轴承承载力进行更加直观的仿真。

需要指明的是，文中所有仿真都是在0.03 mm气膜间隙和30 000 r/min额定转速下进行。螺旋槽型动压气体止推轴承的设计参数，如表1所示。其中：槽宽比为b1/b2；槽端半径比为(Ro-Rg)/(Ro-Ri)。

表1 螺旋槽型动压气体止推轴承的设计参数Tab.1 Design parameters of spiral groove gas bearing

对该气体轴承采用Fluent软件进行流体仿真，其中几个关键步骤[14]为：首先是网格划分，其类型选择结构化网格、密度需比较来确定，关键部位的网格质量也需保证；然后是边界条件的设置，螺旋槽气膜的外环面设定为pressure-inlet，内环面设定为pressure-outlet，螺旋槽面设定为固定不动的wall，光滑平面设定为可高速旋转的moving-wall；其次是Fluent软件的其他相关设置，模型选用Viscous基于线性的黏性模型，求解器选用Pressure-Based Solver基于压力的求解器，算法上选用SIMPLE算法，该算法使用压力和速度之间的耦合关系来促使质量守恒，从而获得压力分布场，松弛因子一般选用默认的亚松弛因子；最后计算时注意残差的收敛情况，一般残差监视器中的能量收敛到1×10-6的数量级，其他变量收敛到1×10-3的数量级或者监视器中的流动变量都不在发生明显变化时，便可以停止迭代。

表1中的型号1气体轴承仿真后得到的气体轴承气膜压力场分布，如图6所示。通过此种方法，最终求得该款螺旋槽型动压气体止推轴承的承载力与气膜间隙的关系，如图7所示。由图7可知，当气膜间隙逐渐减小时，气体轴承的承载力呈现指数级增加的趋势，因此推断，当轴向磁轴承失效时，螺旋槽型动压气体止推轴承可以承担保护轴承功能。

图6 螺旋槽型动压气体止推轴承压力场分布Fig.6 Pressure field distribution of SGGB

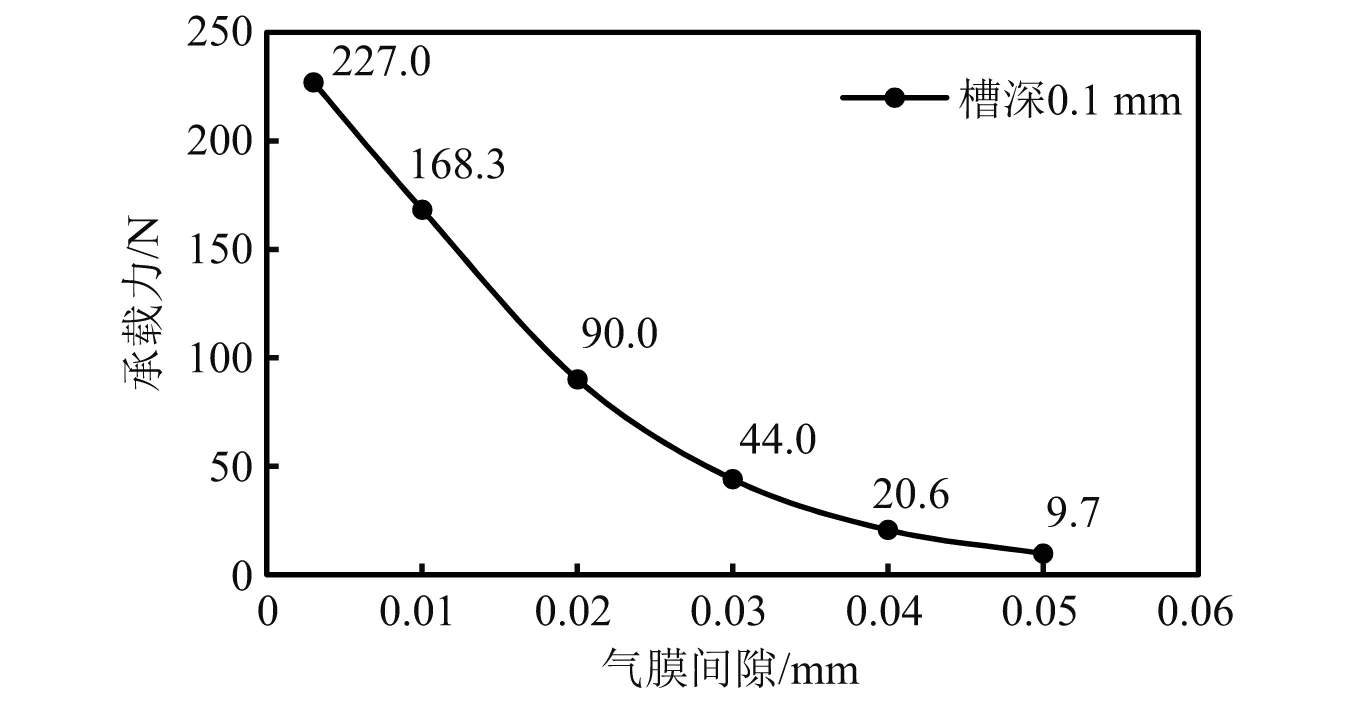
图7 承载力与气膜间隙的关系Fig.7 Effect of air film gap on bearing capacity

2.2 气体轴承结构参数对承载力的影响

2.1节已经给出了气体轴承承载力的仿真方法，按照此种方法，通过逐一改变表1中两组螺旋槽型动压气体止推轴承结构参数的设计值，可分析槽深、槽数、槽宽比、槽端半径比和螺旋角等结构参数对气体轴承承载力的影响[15]。螺旋槽型动压气体止推轴承结构参数的研究变量，如表2所示。

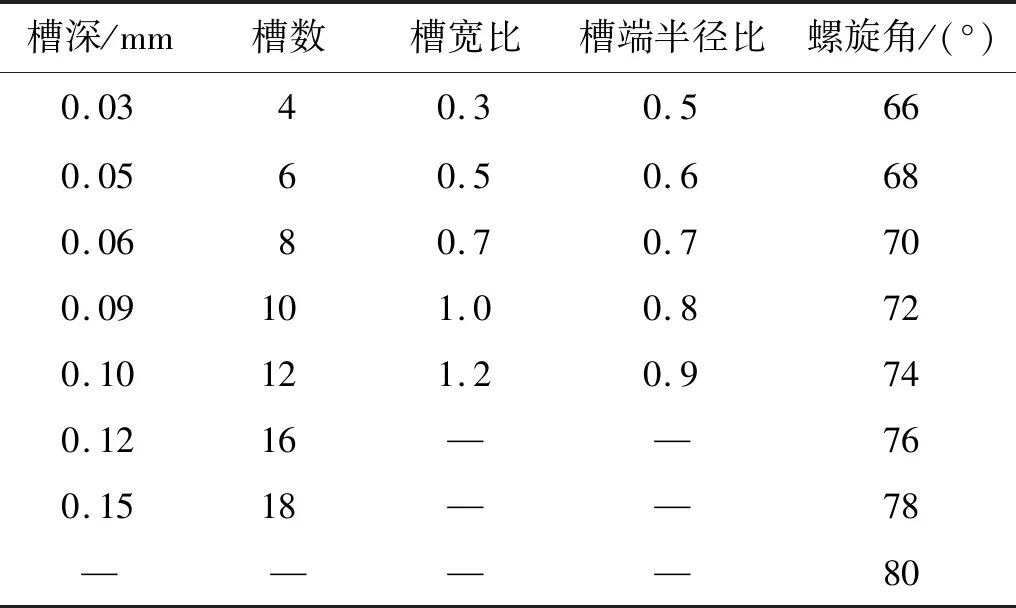
表2 螺旋槽型动压气体止推轴承的结构参数Tab.2 Structural parameters of SGGB

螺旋槽型动压气体止推轴承的承载力与槽深的关系，如图8所示。由图8可知：当气膜间隙为0.03 mm，槽深为0.09～0.10 mm时，承载力较大。

图8 螺旋槽型动压气体止推轴承承载力与槽深的关系Fig.8 Effect of groove depth on bearing capacity

对型号1气体轴承进行分析，型号2 情况相似，螺旋槽型动压气体止推轴承的承载力与槽数的关系，如图9所示。由图9可知：在气膜间隙为0.03 mm的情况下，当槽数大于10时，槽数对于气体轴承的承载力几乎没有影响；在气膜间隙为0.01 mm的情况下，当槽数大于16时，槽数对于气体轴承承载力的影响也非常小。

图9 螺旋槽型动压气体止推轴承承载力与槽数的关系Fig.9 Effect of the groove number on the bearing capacity

螺旋槽型动压气体止推轴承的承载力与槽宽比的关系，如图10所示。由图10可知，气体轴承的承载力随着槽宽比的增大逐渐增大，当槽宽比达到0.7左右后，承载力又随着槽宽比的增大逐渐减小。

图10 螺旋槽型动压气体止推轴承承载力与槽宽比的关系Fig.10 Effect of groove width ratio on bearing capacity

螺旋槽型动压气体止推轴承的承载力与槽端半径比的关系如，图11所示。由图11可知，当槽端半径比为0.7时，气体轴承承载力最大。槽端半径比太小会导致槽区面积减小，不利于动压阶梯效应的产生；槽端半径比太大会导致气体轴承内环封闭区面积减小，使得气体容易泄露，削弱了动压效应。

图11 螺旋槽型动压气体止推轴承承载力与槽端半径比的关系Fig.11 Effect of groove end radius ratio on bearing capacity

螺旋槽型动压气体止推轴承的承载力与螺旋角的关系，如图12所示。由图12可知：当螺旋角在74°左右时，气体轴承承载力最大。螺旋角太小会使气体不容易进入槽区，从而削弱了动压阶梯效应；螺旋角太大会使螺旋线环绕在气体轴承上，这种情况下，很难利用螺旋槽的边沿产生比较好的动压阶梯效应。

图12 螺旋槽型动压气体止推轴承承载力与螺旋角的关系Fig.12 Effect of spiral angle on bearing capacity

根据上述仿真结果，螺旋槽型动压气体止推轴承的基本结构参数优化结果为：①相对于0.03 mm的气膜间隙，槽深取气膜间隙的3倍左右，即0.09～0.10 mm，本文选用0.1 mm；②槽数取14～18个比较合适，槽数太多承载力提升效果不明显，本文选用16个；③槽宽比取0.5～0.7，本文选用0.7；④槽端半径比取0.65～0.75，本文选用0.7；⑤螺旋角取72°～76°，本文选用74°。

3 轴向磁气组合轴承转子系统的试验研究

3.1 磁气组合轴承转子系统的静动态特性试验研究

当磁气组合轴承转子系统静态悬浮时，磁轴承线圈电流和转子位置波形图，如图13所示。由图13可知，转子在轴向和径向的设定位置为2.5 V，轴向磁轴承线圈电流约为0.974 mV，换算成实际电流值约为1.461 A，径向磁轴承线圈电流约为1.7 mV，换算成实际电流值约为2.55 A。

1.轴向磁轴承电流波形图；2.转子轴向位置波形图；3.径向磁轴承电流波形图；4.转子径向位置波形图。图13 静态悬浮电流及位移波形图Fig.13 Waveform of current and displacement during static levitation

当磁气组合轴承转子系统在30 000 r/min高速旋转时，磁气组合轴承转子系统轴向和径向的电流及位移波形图，如图14所示。由图14可知：磁气组合轴承转子系统的轴向振动约为100 mV，换算成实际振动量为0.002 mm；径向振动约为400 mV，换算成实际振动量为0.016 mm。

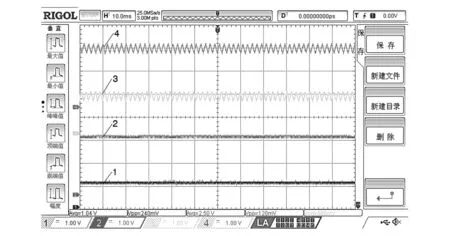
1.轴向电流；2.轴向位移；3.径向电流；4.径向位移。图14 动态旋转电流及位移波形图Fig.14 Waveform of current and displacement during dynamic rotation

3.2 螺旋槽型动压气体止推轴承承载力测试

3.2.1 实际承载力检测方法

轴向磁气组合轴承转子受力分析，如图15所示。此时将气轴承推力盘右侧的气体轴承换成无槽盘，以便测试单一气体轴承的承载力。根据设计，当磁轴承推力盘处于轴向磁轴承中心位置时，气轴承推力盘也处于气体轴承中心位置，此时，磁轴承推力盘与轴向磁轴承的单边气隙为0.25 mm，气轴承推力盘与气体轴承的单边气隙为0.05 mm。

图15 轴向磁气组合轴承转子受力示意图Fig.15 Schematic diagram of force to the rotor of axial magnetic-gasbearing

当磁气组合轴承转子系统的转子稳定悬浮时，由于转速为0，螺旋槽型动压气体止推轴承还没有产生承载力，此时，可以测得磁轴承1的线圈电流i1和磁轴承2的线圈电流i2，则根据式(1)可以得到磁轴承1与磁轴承推力盘的单边气隙z1，以及磁轴承2与磁轴承推力盘的单边气隙z2。求解公式为

(9)

当磁气组合轴承转子系统高速旋转时，再次测量磁轴承1的线圈电流i′1和磁轴承2的线圈电流i′2。此时，根据式(1)可以得到磁轴承1和磁轴承2的磁力大小。求解公式为

(10)

(11)

因此，螺旋槽型动压气体止推轴承的承载力可根据式(10)以及式(11)求得，即

F气=|F′磁1-F′磁2|

(12)

通过调节转子的轴向悬浮位置，即可调整气体轴承推力盘与气体轴承之间的气隙，根据式(12)从而获得不同气隙处的气体轴承实际承载力大小。

3.2.2 气体轴承承载力与气膜间隙的关系试验

气体轴承承载力与气膜间隙关系的试验数据，如表3所示。表中电流i1，i2，i′1和i′2对应式(9)～式(11)推导中的电流。将各个气膜间隙下所对应的电流代入式(9)～式(12)，得到螺旋槽型动压气体止推轴承承载力的大小，此时转子转速为30 000 r/min。

表3 气体轴承承载力与气膜间隙关系的试验数据Tab.3 Test data on the effect of air film gap on bearing capacity of gas bearing

考虑到转子振动量，为安全起见，气膜间隙最小可调整到0.02 mm。利用软件MATLAB曲线拟合工具箱将试验所测得的数据进行拟合，得到如式(13)所示的曲线拟合方程

F气=92.53×e-61.36h0

(13)

式中：F气为气体轴承承载力；h0为气膜间隙。

根据拟合曲线，将0.003 mm，0.010 mm，0.020 mm，0.030 mm，0.040 mm，0.050 mm的气膜间隙代入式(13)可得气体轴承承载力与气膜间隙的拟合关系结果。

气体轴承承载力与气膜间隙关系的拟合结果和试验结果，如图16所示。由图16可知，试验结果所测得的4个点与拟合结果基本一致，据此可认为拟合曲线能够近似表示实际承载力与气膜间隙的关系。由拟合曲线可知，随着气膜间隙的变小，螺旋槽型动压气体止推轴承承载力呈现近似指数级的增长趋势。

图16 气体轴承承载力与气膜间隙的关系(1)Fig.16 Effect of air film gap on bearing capacity of gas bearing (1)

气体轴承承载力与气膜间隙关系的拟合结果和仿真结果，如图17所示。由图17可知，拟合结果与仿真结果存在一定误差，但趋势基本一致，承载力随着气膜间隙的变小都呈现了近似指数级的增长趋势。

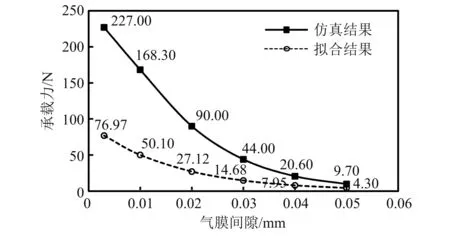
图17 气体轴承承载力与气膜间隙的关系(2)Fig.17 Effect of air film gap on bearing capacity of gas bearing (2)

由于螺旋槽型动压气体止推轴承表面与气体轴承推力盘表面存在平行度和平面度误差，因此拟合结果与仿真结果存在误差。气体轴承与气轴承推力盘不平行，此时通过百分表测量的气膜间隙为点a到气轴承推力盘的距离，然而实际气膜间隙要大于试验测量记录的气膜间隙，根据图17的仿真结果，当实际气膜间隙较大时，动压气体轴承的实际承载力会减小很多，即使平行度超过0.005 mm，仿真结果与试验结果也会产生较大的误差，如图18所示。

图18 气体轴承推力盘与气体轴承的平行度Fig.18 Parallelism of gas bearing thrust disc and gas bearing

3.2.3 气体轴承承载力与转速的关系试验

气体轴承承载力与转速关系的试验数据，如表4所示。表中电流i1，i2，i′1以及i′2对应式(9)～式(11)推导中的电流。将各个转速下所对应的电流代入式(9)～式(12)，得到螺旋槽型动压气体止推轴承承载力的大小，此时气体轴承气膜间隙为0.02 mm。

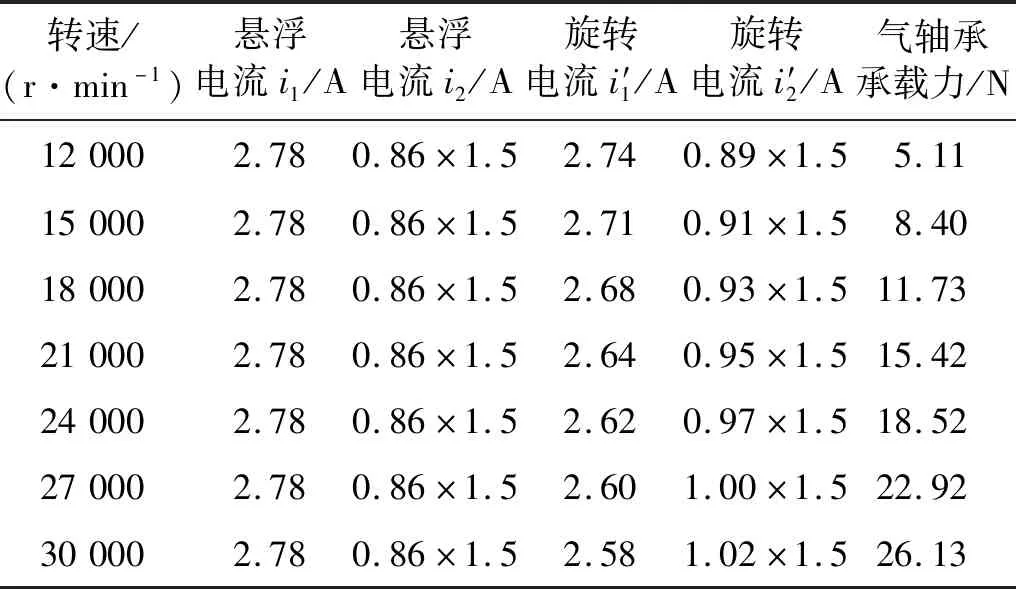
表4 气体轴承承载力与转速关系试验记录Tab.4 Test data on the effect of speed on bearing capacity of gas bearing

气体轴承承载力与转速关系的试验结果和仿真结果，如图19所示。由图19可知，随着转速的提高，气体轴承承载力呈现近似线性增长的趋势。试验结果与仿真结果存在一定误差，产生误差的原因与3.2.2节的分析相同。

图19 气体轴承承载力与转速的关系Fig.19 Effect of speed on bearing capacity of gas bearing

3.2.4 气体轴承作为保护轴承的试验验证

无槽盘跌落试验过程为：①用无槽盘代替螺旋槽型动压气体止推轴承，并装配到试验台的相应位置；②利用磁轴承使转子悬浮到平衡位置，并打开变频器将转子加速到30 000 r/min；③切断轴向磁轴承电源，气体轴承推力盘和无槽盘急速摩擦，转子约在5 s后停转。

气轴承跌落试验过程为：①将无槽盘取下，装上螺旋槽型动压气体止推轴承，并换上新的气体轴承推力盘；②利用磁轴承使转子悬浮到平衡位置，并打开变频器将转子加速到30 000 r/min；③切断轴向磁轴承电源，气轴承推力盘和螺旋槽型动压气体止推轴承高速摩擦，转子约在10 s后停转。

跌落试验结果分析如下。

(1)从表面磨损程度分析：无槽盘做跌落试验的表面磨损情况，如图20所示。无槽盘的表面有一圈磨损比较严重的痕迹，且表面材料出现了剥落情况，这是因为无槽盘表面因为转子瞬间跌落，在高速摩擦下产生的高温所引起的。螺旋槽型动压气体止推轴承做跌落试验的表面磨损情况，如图21所示。气体轴承表面只出现了轻度摩擦痕迹，这是因为转子跌落瞬间，气体轴承和气体轴承推力盘之间的气膜间隙瞬间变小，再结合高速旋转的作用，气体轴承瞬间产生了非常大的支承力，进而阻止了气体轴承推力盘与螺旋槽型动压气体止推轴承的严重摩擦，直到转子转速下降至一定值时，气体轴承推力盘才和气体轴承产生接触摩擦，因此损伤程度较小。

图20 无槽盘表面磨损图Fig.20 Surface wear diagram of grooveless disk

图21 气体轴承表面磨损图Fig.21 Surface wear diagram of gas bearing

(2)从转子停转时间分析：装上无槽盘的转子，在高速跌落后约5 s便停转；装上螺旋槽型动压气体止推轴承后，转子在高速跌落后约10 s才停转。据此可以判断，在转子跌落的初期，螺旋槽型动压气体止推轴承产生了非常大的支承力，使得转子在空气动压的作用下继续旋转，直到转子转速下降至一定值时，转子上的气体轴承推力盘才和气体轴承产生接触摩擦，使得转子停止转动。

4 结 论

(1)对螺旋槽型动压气体止推轴承的结构参数进行了仿真优化，优化的结果为槽深取0.1 mm、槽数取16个、槽宽比取0.7、槽端半径比取0.7、螺旋角取74°。

(2)研究了轴向磁气组合轴承转子系统的静动态特性，当径向自由度采用磁轴承并且轴向自由度采用磁气组合轴承时，系统能够稳定悬浮，并且安全运行至工作转速30 000 r/min，达到工作转速时，转子的径向振动为0.016 mm，轴向振动为0.002 mm。

(3)测试了螺旋槽型动压气体止推轴承承载力与气膜间隙和转速之间的关系，随着气膜间隙的减小，气体轴承承载力呈现近似指数级的提高，随着转速的增加，气体轴承承载力呈现近似线性增长的趋势。当转速为30 000 r/min、气膜间隙为0.02 mm时，气体轴承承载力的测试结果为26.83 N。由试验结果拟合预测0.003 mm气膜间隙下，气体轴承承载力可达到76.97 N。

(4)通过转子高速跌落试验，验证了螺旋槽型动压气体止推轴承作为保护轴承的有效性。螺旋槽型动压气体止推轴承，因其承载力与气膜间隙以及转速的特有关系，在高转速小气膜间隙条件下，能够产生较大的承载力，减轻转子直接撞击造成的严重损害；在低转速条件下，动压气体轴承承载力迅速降低，转子和动压气体轴承会产生损伤程度较小的接触摩擦。