Ab initio方法研究40Ca35Cl分子的自旋轨道耦合效应和跃迁性质

杨全顺, 杨彦广, 方 明, 万明杰

(1. 中国空气动力研究与发展中心 超高速空气动力研究所， 绵阳 621000; 2. 宜宾学院 物理与电子工程学院， 宜宾 644007)

1 前 言

碱土金属氯化物是离子化合物[1]，它的电子结构通过单个价电子最外面的两个闭壳层离子来描述，位于金属离子周围的电子被负离子场极化. 碱土金属氯化物还为天体物理[2]，晶体和高温化学[3]的研究提供了独特的机会. 特别是，由于40Ca35Cl分子在行星大气中丰富的含量，导致天体物理学家对其有强烈的研究兴趣. 此外，CaF分子在实验上已经成功冷却到mk温度，并打破了多普勒冷却极限，而Cl和F处于同一主族，所以有理由相信，40Ca35Cl分子也有可能会被冷却到很低的温度. 因此，40Ca35Cl分子精确的物理量(例如，吸收线，光谱常数，辐射跃迁数据等)的计算变得至关重要.

对于40Ca35Cl分子，无论是在理论[4,5]还是实验[6-12]上，多位研究者已对其做了细致的分析，特别是对于它的三个低激发态(A2Π, B2Σ+和C2Π). 早在1973年，Dagdigian等人就对碱土金属氯化物的A2Π1/2,3/2, B2Σ+和C2Π1/2,3/2态的辐射寿命进行了测量，之后，L. -E. Berg 等人使用激光光谱仪对CaCl的A2Π → X2Σ+跃迁做了转动分析，同年，L. Klynning and H. Martin获得了气态CaCl分子的X2Σ+态的势能曲线. 1986年，Ernst和Kändler测量了CaCl分子的A2Π和B2Σ+态的电偶极矩，另外，Raouafi等人计算了CaF和CaCl分子不同态的永久偶极矩和跃迁偶极矩. 目前调研发现，尽管分子的三个低激发态已经被详细的研究，但是运用从头算方法获得的数据并不是很精确，并且，对于12Δ态，目前还没有理论和实验的相关报导，此外，除了BREG等人测量了D2Σ+和E2Σ+态的辐射寿命外，对于高激发态D2Σ+和E2Σ+，没有更详细的理论和实验描述.

基于以上考虑，我们采用Abinitio方法研究40Ca35Cl分子基态和激发态的自旋轨道耦合效应和跃迁性质. 文章的组织如下：第二部分是对方法的简要陈述；第三部分对计算结果和实验数据进行了详细的对比；第四部分是对本文工作的总结.

2 方 法

完全活性空间自洽场(CASSCF)[13,14]方法用于40Ca35Cl分子7个Λ-S低电子态的态平均计算，在此计算中，能量在12步迭代之后收敛. 之后，运用CASSCF计算的波函数作为参考波函数，多参考组态相互作用(MRCI)[15,16]加Davidson(+Q)[17]纠正方法被使用，在MRCI方法中，能量在18步迭代之后收敛.

由于Molpro[18]软件的限制，必须使用阿贝尔点群来描述分子轨道. 在CASSCF计算中，我们将Ca(1s22s22p63s23p6)和Cl(1s22s22p63s23p6)的36个电子放置在闭壳层轨道，闭壳层轨道则为(10,4,4,0). 由于电子要跃迁到高激发态，所以在计算中需要涉及空轨道，由空轨道和价电子轨道组成活性轨道. 随后的MRCI方法使用相同的闭壳层轨道和活性轨道. 对于Ca原子和Cl原子，在计算中我们都使用了全电子基组. Ca使用的是弥散性相关一致极化价4重基组[19]，Cl使用相关一致极化价4重基组[20]，由于资源的限制，对于相对论效应和更大的基组我们在计算中都没有考虑. 在之后计算自旋轨道耦合效应时，我们使用了相同的轨道空间和基组.

基于获得的势能曲线，运用level[21]程序，我们得到了7个Λ-S低电子态和6个Ω的光谱常数，获得的数据与实验值非常符合，要好于之前的理论计算结果.

3 结果和讨论

3.1 势能曲线和光谱常数

图1呈现了40Ca35Cl分子7个低电子态的势能曲线，拟合的光谱常数和之前的理论和实验值一起罗列在表1中. 从表1中可以看出，我们目前所获得的光谱常数与实验值非常符合. 比如，基态的非谐波频率(ωeχe)与实验值相同，平衡键长(Re)和谐波频率(ωe)与实验非常接近，两者与实验值的误差分别为0.2%和1.1%；对于A2Π态，除了非谐波频率(即使如此，我们获得的值仍然要优于Bergetal[7]的计算结果)，其它的光谱常数都与实验值很接近. 值得注意的是，到目前为止，无论是实验还是理论，都没有对40Ca35Cl分子12Δ态的报道，因此，我们希望目前的数据可以为之后观察12Δ态提供一个良好的理论参考.

图1 在MRCI下计算的7个Λ-S态的势能曲线Fig. 1 Calculated potential energy curves of seven Λ-S states of the 40Ca35Cl molecule at the MRCI level of theory.

表1 在多参考组态相互作用下计算得到的40Ca35Cl分子束缚态的光谱常数

表2 在多参考组态相互作用下计算得到的40Ca35Cl分子六个Ω态的光谱常数

表3 计算获得的40Ca35Cl分子A2Π和C2Π在平衡键长处的自旋轨道分裂值和之前的理论计算结果以及实验值(单位为cm-1)

另外，我们还使用RKR[23,24]方法拟合了X2Σ+和A2Π态在平衡键长附近的势能曲线，RKR方法获得的曲线和我们得到的曲线一起呈现在图2中. 从图2中可以看出，RKR拟合的曲线与我们目前的曲线几乎重合. 另外，通过求解一维薛定谔方程，使用我们得到的势能和RKR势，获得了v=0-11的振动态的项值和转动常数，结果显示，运用两种势得到的项值和转动常数非常一致. 此外，我们还获得了v=12-40的项值和转动常数，希望这些值可以为40Ca35Cl分子在实验上的观察提供有力的帮助.

图2 40Ca35Cl分子X2Σ+和A2Π态势能曲线和RKR的比较Fig. 2 Compared with the RKR potential for the X2Σ+ and A2Π states of 40Ca35Cl.

通过在Breit-Pauli近似[25]下的SOC算符，我们还考虑了40Ca35Cl分子自旋轨道耦合效应的影响. 6个Ω态的势能曲线和光谱常数分别呈现在图3和表2中. 比较考虑了SOC耦合和没有考虑SOC耦合的光谱常数，我们发现，得到的光谱常数并没有发生很大的改变，这可能是由于40Ca35Cl分子比较轻的原因. 另外，我们还在表3中罗列了态在平衡键长处实验和理论计算的分裂，从表3中可以看出，我们目前的计算结果要更加接近实验值. 这也进一步说明我们之前计算的势能曲线的正确性.

图3 在MRCI下计算的6个Ω态的势能曲线Fig. 3 Calculated potential energy curves of six Ω states of the 40Ca35Cl molecule at the MRCI level of theory.

3.2 跃迁偶极矩和永久偶极矩

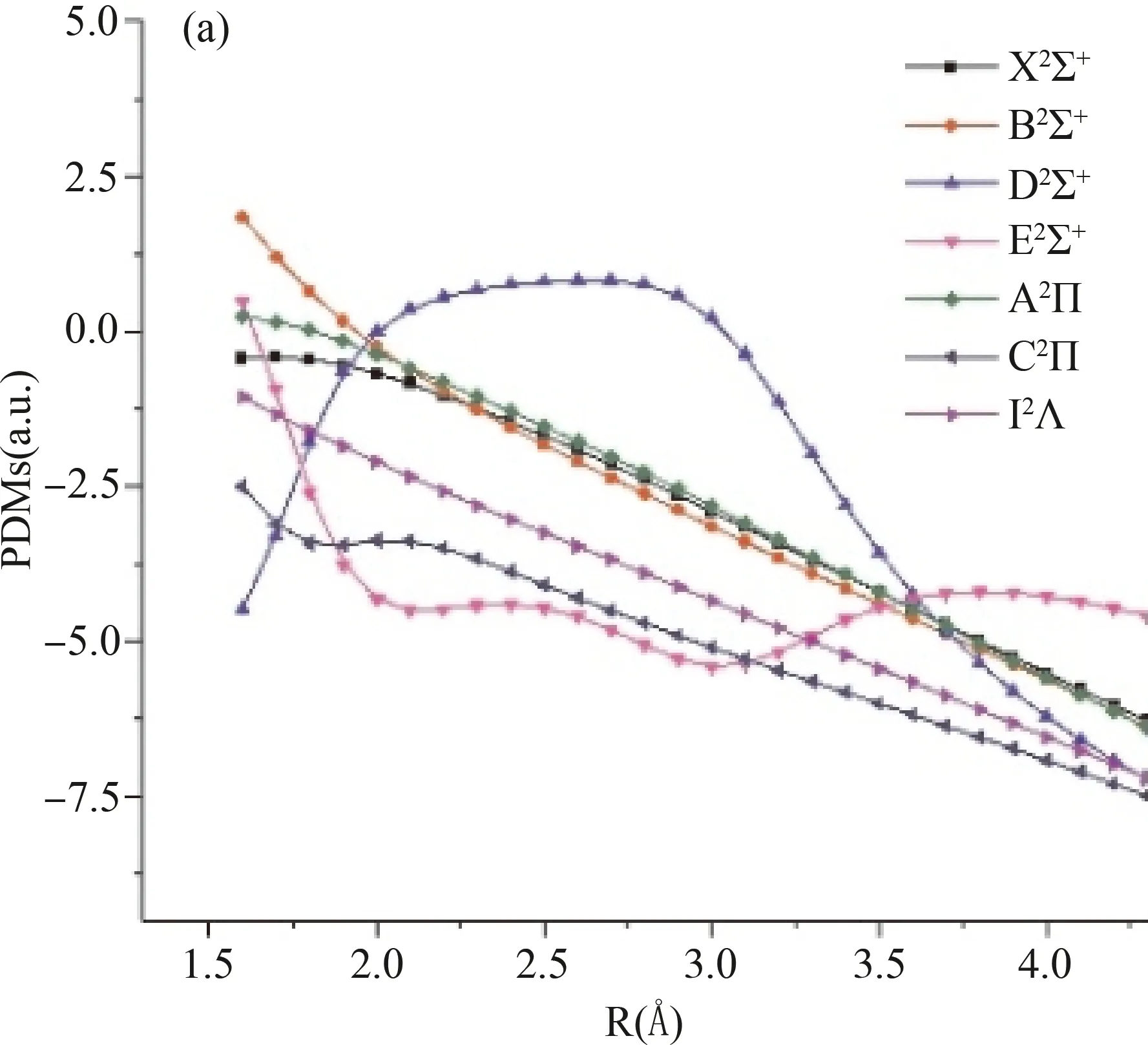
图4呈现出了40Ca35Cl分子在MRCI级别的7个低态的永久偶极矩和A2Π →2Σ+, 12Δ以及C2Π →2Σ+, 12Δ跃迁的跃迁偶极矩. X2Σ+,A2Π, B2Σ+和A2Π态在平衡键长位置的永久偶极矩和A2Π → Χ2Σ+，B2Σ+以及A2Π → Χ2Σ+跃迁偶极矩的数值和之前计算的理论和实验数据一起罗列在表4和表5中，从表4和表5中的数值可以看出，我们目前的计算结果与实验值更符合，也就是说，我们目前获得的永久偶极矩和跃迁偶极矩是可靠的. 另外，对于C2Π →2Σ+, 12Δ的跃迁，目前还没有理论计算和实验观察，因此，我们目前的得到的数据可以为之后的实验观测C2Π →2Σ+, 12Δ跃迁做一个有益的参考.

表4 40Ca35Cl分子在平衡键长处的永久偶极矩

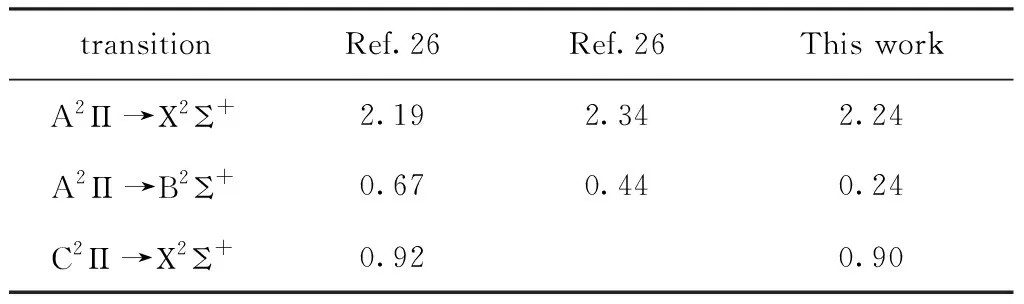
表5 40Ca35Cl分子在平衡键长处的跃迁偶极矩

4 结 论

运用Molpro量化软件，我们获得了40Ca35Cl分子7个Λ-S低电子态的势能曲线和永久偶极矩，以及A2Π →2Σ+, 12Δ和C2Π →2Σ+, 12Δ跃迁的跃迁偶极矩. 获得的光谱常数(不管是考虑了SOC还是没有考虑SOC)要好于之前的理论计算结果且更接近于实验值. 另外，我们得到了7个Λ-S低态的永久偶极矩，并于之前的理论计算进行了对比，发现目前的计算结果与之前的结果符合的很好. 此外，使用我们得到的势能和RKR势，获得了v=0-11的振动态的项值和转动常数，结果显示，运用两种势得到的项值和转动常数非常一致. 值得注意的是，由于获得的永久偶极矩和跃迁偶极是正确可靠的，我们还首次呈现了C2Π →2Σ+, 12Δ跃迁的跃迁偶极矩. 希望本文呈现的结果可以为之后观察40Ca35Cl分子的高激发态光谱和跃迁性质以及激光冷却提供有益的理论参考.