精设活动，激发思考，生长能力

胡俊

[摘  要] 文章从活动设计的视角详细记述了“摆一摆，想一想”这节课的教学过程，谈谈如何精设活动，引发数学思考、揭示本质、生长能力。通过教学实践，研究者提出数学教学中合适的问题情境是深度思考的保障，精巧的数学活动让学生经历完整的思考过程，及时感悟是能力生长的重要途径。

[关键词] 数学活动;深度思考;能力

新课改风向标下，从学生“双基”的培养到“三维目标”的落实，再到今天的核心素养，一路走来，不少教师的教学观念也随之改变，逐步意识到课堂教学的重心应转向学生的“学”。但如何实现真正意义上的转型，如何提出问题，如何精设活动，不少教师并没有真正思考，仅仅是停留在形式上的转变。笔者在课堂教学中进行了有意义的尝试，现以“摆一摆，想一想”这节课的教学为例，与各位同行交流、研讨。

一、课前慎思

1. 学生的学习基础是什么？

在本节课之前，不少学生已经接触过100以内的数，并初步掌握了“数位的意义”，同时对不同数位上的数表示不同的数值也有了一定程度上的理解，当然有小部分学生也可以数出1000以内的数。

2. 此类课程的教学一般有怎样的过程？

本课是一次实践活动课，属于一种新型的学习活动，也是新课程提出的四大学习领域中的一大重点。我们杜绝运用“告知”“传输”等方式，而是通过数学活动，让学生在主动参与的过程中操作、思考、探究、交流和体悟，同时加深对数与代数等内容的认识和理解。

3. 本课的教学目标是什么？

通过本课教学，要深化学生对100以内数的认识，还要让学生在经历操作、猜测、验证的活动过程中理解数位与位值的概念，引发深度思考，发展合情推理，渗透数学思想，促进数感的形成。学生在合作、交流、聆听、辩论等过程中，丰富了自身的体验，学会有条理地阐述自身的认识和想法，培养了合作学习的能力。本课的教学重点是让学生在深度思考中提炼规律，难点是发展学生合情推理的能力和促进学生数感的自然形成。

二、课中笃行

1. 情境展现，在旧知中感知

师：今天老师请来了你们的一位“老朋友”，可还认识？（呈现数位表）

生（齐）：认识。

师：那下面谁愿意代替它做个自我介绍呢？

生1：它是数位表，有十位和个位两个数位。

师：介绍得清楚又简洁，很棒！大家看，这里还有一个圆片，倘若我们要用它在数位表上表示10，该如何操作呢？

生2：只要将它摆在十位上。

师：不错，将它摆在十位上，即表示1个十，就是10。

师：那它还可以在数位表上表示其他数吗？该如何摆呢？

生3：把它放在个位上，即表示1个一，就是1。

师：你们看，一个小小的圆片也可以创造出不同的数，是不是很神奇？今天我们就一起来摆一摆，想一想，探寻更多的奥秘！（板书课题）

设计意图：本教学片段把已学的“数位表”以情境的方式再现，并以解决问题的方式让学生理清数位和位值的概念，让学生感知“摆一摆，想一想”的乐趣，从而为进一步发现和思考奠定良好的基础。

2. 寻求规律，在活动中思考

活动1：2个圆片可以摆出哪些数呢？

师：适才我们用1个圆片摆出了两个不同的数，现在给大家2个圆片，可以摆出哪些数呢？大家一起来试一试吧！（学生投入操作，教师来回巡视）

师：下面哪位学生愿意分享你的成果呢？

生4：大家看，十位和个位上各有1个圆片，组成11。

师：生4摆得不错，解说得也清晰，我们一起记下结果。（教师记录并展示表1）

生5：十位上放2个圆片，组成20。

生6：个位上放2个圆片，组成2。

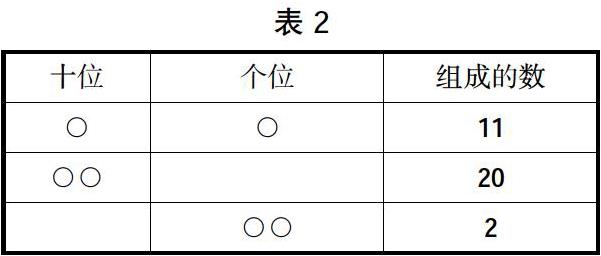
师：谁能将生5和生6的结果也如老师一样记录呢？（学生争先恐后地將结果展示在表2中）

设计意图：有了前面1个圆片的体验，本教学片段以2个圆片为背景，引领操作活动，引导互相冲突的思维，让学生进一步领悟摆圆片活动的过程，即思考如何摆—动手摆—结合摆法写数—记录结果，从而架起具体操作与抽象互通的桥梁，为进一步抽象奠基。

活动2：3个圆片可以摆出哪些数呢？

师：现在再增加1个圆片，大家再来试一试，并记录结果。（教师巡视）

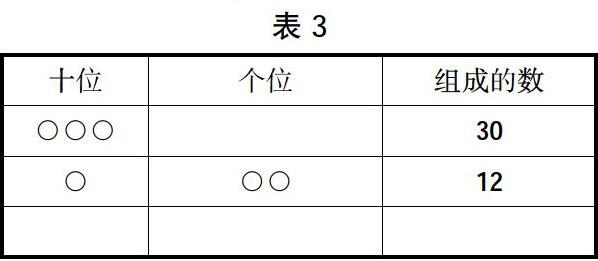
生7：我的结果见表3。

师：生7摆了两个数，其他同学呢？

生8：表4是我的结果。

师：生8摆出了4个数。

生9：我也摆出了4个数，但和他不同，见表5。

师：你们更喜欢哪种摆法呢？请小组交流，然后将观点与全班分享。

生10：我喜欢生9的摆法，他是按照从大到小的顺序依次摆放的。

师：很好，这种摆法是依序而摆的，这样不易遗漏和重复。那大家再思考一下，是否还有其他摆放的顺序？

生11：还可以依照从小到大的顺序摆放……

设计意图：活动2在活动1的基础上更深了一步，用表格表示，让学生的思考更进一步。接着由能摆几个数联想到不遗漏、不重复摆出所有数的方法，形象地展示了有序思考的方法，形成了有序思考的数学思想的雏形。

活动3：思考4个圆片可以摆出哪些数。（具体过程略）

设计意图：剥离实践的参与，在有序思考的指引下，学生写出能摆的所有数，进一步培养了学生的抽象思维能力，推动了数感的形成。

活动4：思考圆片个数与摆出的数之间有何关系。

师：我们先来猜测一下，7个圆片可以摆出多少个数呢？

生12：8个，分别为70，61，52，43， 34，25，16，7。

生13：我得出的数是7，16，25，34， 43，52，61，70。

师：他们都是按顺序写出的，大家一起观察生13写出的数，有何发现？（陷入深思）

生14：1+6=7，2+5=7……

生15：两个位数上的数字相加即为圆片的个数。

师：非常好，观察很仔细，那这个发现仅仅是7个圆片摆出的数才具有的吗？我们一起再来回顾刚才所摆的數，也具有这样的规律吗？（出示课件）

生（齐）：都具有这个规律。

师（拾级而上）：圆片个数与摆出的数二者有何关系？谁能说一说呢？请大家讨论，稍后与大家分享你的想法。

生16：圆片个数比摆出的数的个数少1。

设计意图：本环节聚焦规律的提炼，让学生在总结的过程中形成深刻的认识。

3. 练习体悟，在提炼中生长

师：我们的同学不仅学会了摆数，还找寻到了其中的规律，真是厉害！下面请完成几道练习题。

练习1：9个圆片可以摆出（  ）个数。

练习2：熊大想到一个惩罚光头强的方法，并将这个方法锁在一个密码箱中，然后告知熊二密码为两位数，十位与个位上的数字相加等于10，且这个密码比90大，你能帮助熊二打开这个密码箱吗？

设计意图：通过两个练习题梳理新知是为了将这些问题反映出的规律渗透进学生的思想之中，促进学生能力的自然生长，让学生的情感得以升华。

三、课后明辨

1. 合适的问题情境是深度思考的保障

规律是高度概括的产物，从具体情境中抽象而得。用合适的问题情境引发学生的深度思考，利于思维的生长。在本节课中，教师设计的问题都具有针对性、层次性和开放性，利于学生在解决问题的过程中分析、思考、质疑、辨析等，引发了不同程度的思考，从而将学生的思维引入深处，进一步领悟数学方法，探寻出规律，实现思维的自然生长[1]。

2. 精巧的数学活动让学生经历完整的思考过程

要让学生获得深层次的感知和感悟，需要开展精巧的数学活动，让学生经历完整的思考过程。本节课中，教师为学生的积极参与提供了有效调控，每个活动的过程都是精心设计的，每个活动中的问题都具有一定程度的开放性，在激起学生积极参与的同时，让学生经历完整的思考过程，并获得成功，发现和总结出规律[2]。

3. 及时感悟是能力生长的重要途径

规律反映了世间万物蕴含的共性，数感的形成和推理能力的培养需要在潜移默化中逐步进行，在学生头脑中固化这些需要一个漫长的过程，需要教师在日常教学中一以贯之地渗透，也需要学生的适时感悟和及时反思。本课中，教师多次创造感悟和体验的机会，在活动中直接诱发学生的直觉，使其进行合情推理，同时在练习中让学生通过不断体悟自然形成数感，使学生在浓郁的“数学味”中生长能力。

参考文献：

[1]  马华平. 核心问题引领，在深度学习中逼近数学本质[J]. 数学教学通讯，2019（16）.

[2]  卞建娣. 精心设计教学活动  促进学生数学思考[J]. 小学教学参考（综合），2019（05）.