考虑多种运行状态的台区拓扑辨识
2021-09-14曾顺奇吴杰康刘国新
曾顺奇,吴杰康,李 欣,刘国新
(1.广东电网有限责任公司广州供电局,广东 广州 510000;2.广东工业大学自动化学院,广东 广州 510006)
0 引 言
配电网的拓扑辨识分析为电力系统的仿真、状态估计、动态潮流计算和故障诊断等计算模块提供了基础的网络结构数据[1],但随着城市人口数量的剧增以及人们对供电可靠性要求的日益提高,这导致了配电网接线的复杂程度与规模不断加大,进一步加大了配电网拓扑的难度,大大降低了配电网拓扑的效率。所以针对降低配电网拓扑难度,提高拓扑效率的研究越来越多。
配电网拓扑辨识的实质就是根据网络中各个断路器的状态来判断网络中各个元件的连接关系,再将网络进行母线分析与电气岛分析[2]。文献[1]运用了分布式网络拓扑并行加速的技术,将整个网络拓扑进行划分,由不同的服务器进行并行加速,充分提高了网络拓扑的效率。文献[2]针对邻接矩阵具有对称性,并将对称性应用到对邻接矩阵进行节点消去简化的过程中,相对于传统的矩阵法辨识,减少了一半左右的计算量,大大提高了拓扑效率。文献[3]针对邻接矩阵是稀疏矩阵,具有稀疏性,将稀疏矩阵技术应用到矩阵拓扑优化中提高拓扑效率。文献[4]针对邻接链表的储存图表示不够直观的缺点,提出了邻接矩阵染色法,使得拓扑过程直观、快速、有效。以上文献通过不同的方法对拓扑过程进行改进优化,也取得不错的效果,但是这些改进均局限于全局拓扑,而未对局部拓扑进行研究。当网络中某个断路器因为配电线路发生故障而导致变位,此时网络的结构可能发生了变化,需要重新拓扑,但直接进行全局拓扑会造成计算资源的浪费。因为变位断路器只影响同电压等级的母线形成[5],即变位断路器只影响局部网络的拓扑,而非全局网络的拓扑。而且,在正常情况下,配电系统中多个断路器的状态同时发生变化的情况是极少的,就算是调度员进行调度,也不会一次性关断许多断路器,所以局部拓扑的适用范围广。文献[6]针对局部拓扑辨识,提出了树搜索法,以断路器断开的一端母线为起点进行树搜索,但并未考虑联络开关闭合的情况,这样会加大树搜索的难度,而且树搜索法面对配电网中复杂的节点和环网,拓扑时间也会大大加长,拓扑效率较差。因此,针对这些情况,需要对网络的局部拓扑进行研究。
综上所述,下面提出一种改进矩阵算法,将网络的拓扑辨识分为全局拓扑、局部拓扑两个过程,并对两种拓扑辨识分别进行改进。
1 考虑运行状态的全局拓扑辨识
矩阵法的全局拓扑辨识,即对得到的全连通矩阵进行分析,以此来对整个网络进行拓扑辨识。全局拓扑,首先将反映网络中节点-支路连接关系的关联矩阵与它的转置进行一次乘法运算得到邻接矩阵;然后使用邻接矩阵法,即对邻接矩阵进行最多次(n-1)的自乘运算(n为邻接矩阵的阶数),当任意两次自乘运算得到的结果一致时,停止自乘运算,所得结果就是全局拓扑需要的全连通矩阵;最后对全连通矩阵进行行扫描、母线分析和电气岛分析,进而得到整个网络的拓扑分析。但是,当网络中节点数目非常多的时候,矩阵法需要占用大量的内存资源,而且拓扑速度变慢,拓扑效率变低。所以,要对矩阵法做出如下改进:
1)使用节点消去法代替邻接矩阵法来处理邻接矩阵,即对邻接矩阵中不重要的节点的行和列删除,只留下重要节点,减少邻接矩阵的阶数;
2)对使用节点消去法所求得的连通矩阵直接使用行扫描法,不需要求取全连通矩阵。
通过这两个方面对矩阵法进行改进,可以很好地减少运算量,提高拓扑效率。
1.1 关联矩阵
在进行网络拓扑的过程中,可以用关联矩阵来表示网络中的连接情况。关联矩阵是描述网络中节点-支路(或者支路-节点)之间连接情况的矩阵。对于一个包含n个节点和m条支路的网络,可以用一个n×m阶矩阵A=[aij]来表示,矩阵的每一行对应于网络中的一个节点,矩阵的每一列对应于网络中的一条支路。如图1所示的网络,从物理模型到数学模型的过程中,即从网络到关联矩阵的过程中,应该把网络中的节点作为关联矩阵的行,把网络中的支路作为关联矩阵的列。关联矩阵中的元素aij的取值表示节点i与支路j的连接情况。aij=1,即节点i与支路j相连接;aij=0,则节点i与支路j不相连。
首先,进行全局拓扑的目的是获取整个网络的全局拓扑模型,为之后的局部拓扑提供必要的拓扑信息。所以,网络中所有的支路断路器(除联络断路器、厂站之间的支路断路器以及变压器之外)都默认为处于闭合状态。支路断路器状态矢量S为

对于图1中网络,关联矩阵A为
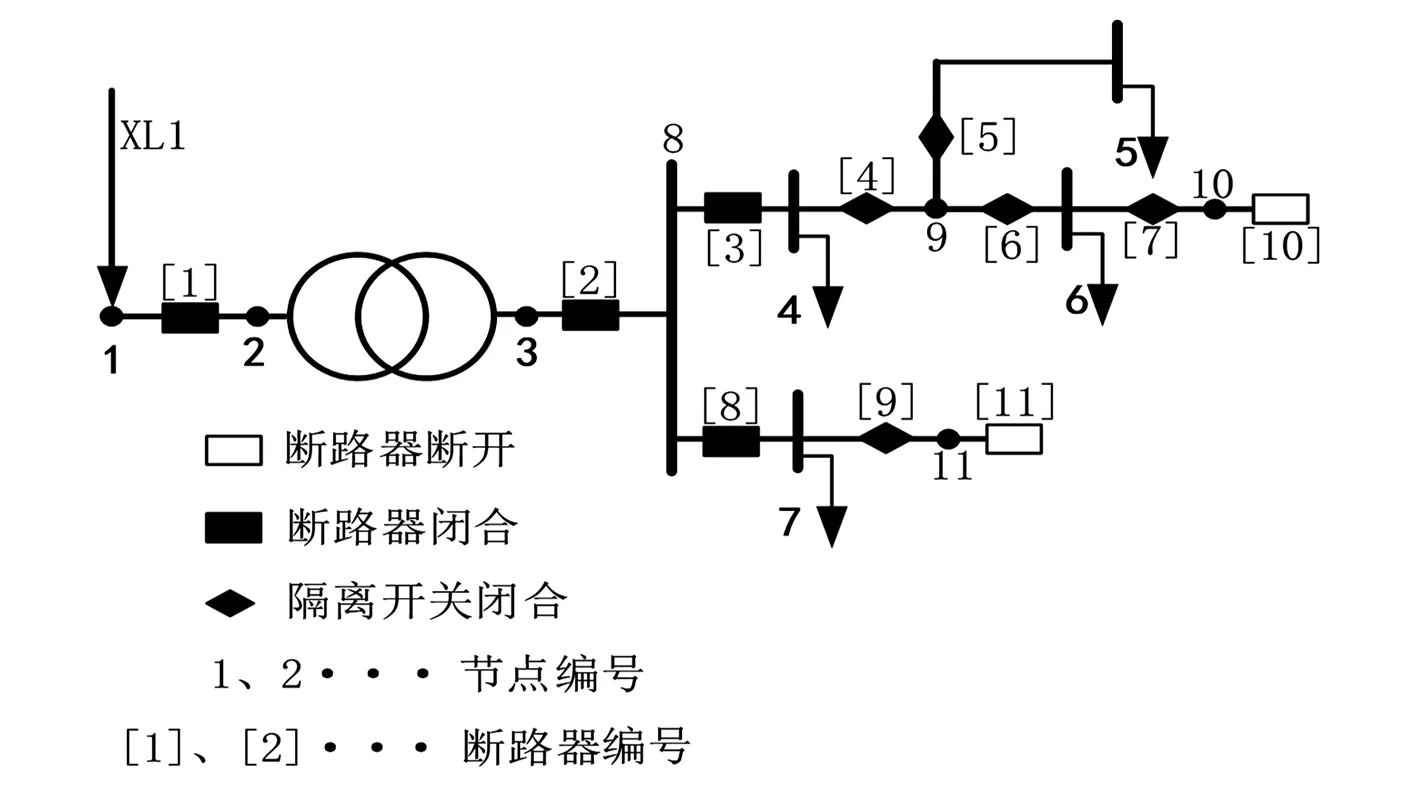
图1 正常的低配电网台区网络

1.2 邻接矩阵
1.2.1 邻接矩阵与关联矩阵的联系
邻接矩阵是描述网络图中节点-节点之间连接情况的矩阵。对于一个包含n个节点的网络,可以用一个n×n阶矩阵B=[bij]来表示。如果两个节点之间通过一条支路直接连接,则bij=1,否则bij=0;而对角线的元素则恒等于1,即bii=1,因此邻接矩阵一定是对称矩阵。因为相连节点之间是靠支路来连接的,所以可以通过反映节点-支路连接关系的关联矩阵来得到相对应的邻接矩阵。对于有个n节点、m条支路的网络,关联矩阵与邻接矩阵的运算式为:
B=A·AT
(3)
式中:A为节点-支路的关联矩阵;B为节点-节点的邻接矩阵。
对于图1中网络,邻接矩阵B为

1.2.2 邻接矩阵的简化
在用矩阵法对网络进行拓扑时,虽然矩阵的数据结构简单,易于理解,不受接线方式变化的影响,适用于复杂的接线网络。但网络中的节点众多,所形成矩阵的阶数十分大,这将给存储空间带来巨大的压力,使邻接矩阵自乘法的运算量呈爆炸式增长,导致网络拓扑的速度变慢。而网络拓扑就是要求实时性,所以需要对矩阵法进行一些改进。
由于网络拓扑并不需要知道所有节点之间的连接情况,其目标就是将重要节点(厂站之间的支路节点、变压器节点、供电电源节点、负荷节点)之间的连接情况反映出来。所以可以将剩下的节点消去降低邻接矩阵的阶数,减轻存储压力,加快拓扑速度。
若两个节点通过一条支路直接连接,则称这种连接关系为一级连通关系;若节点i和节点j通过节点k间接连接,则称这种连接关系为二级连通关系,以此类推。
如图1所示,图中有11个节点,其中属于重要节点的有1、2、3、4、5、6、7,也就是说,只需要知道节点1—7的连接情况,其他的节点都可以消去。将矩阵中的元素更新后,就将矩阵中要消去节点的行和列删去,则矩阵的阶数降低一阶。节点消去的运算式为
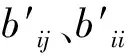
邻接矩阵元素更新后,将矩阵中的第k行、第k列删去。
若将节点8消去,根据邻接矩阵B可知,节点3、节点4、节点7这些重要节点通过节点8形成二级连通关系,所以将节点8消去后,可得矩阵B′为

将B′所有不重要的节点都消去后,就可得到连通矩阵C为

1.3 全连通矩阵
所得到的连通矩阵C并不是想要得到的全连通矩阵,还需对连通矩阵C进行最多(n-1)次自乘运算(n为连通矩阵的阶数),当任意两次自乘运算的结果都一样时,则得到了全连通矩阵T为

最后对全连通矩阵进行行扫描、母线分析和电气岛分析。
在上述步骤中,可以将求取全连通矩阵的步骤删去。因为对全连通矩阵进行行扫描,即是对矩阵中行向量的线性相关性进行判别,而这些行向量的线性相关性在所得到的连通矩阵中就已经存在了,而不是在求取全连通矩阵的过程中出现的。所以,可以直接对连通矩阵使用行扫描法。行扫描法的运算式为
C′(i)=C′(j)=[C(i)⊕C(j)]
(10)
式中:C(i)、C(j)为连通矩阵中行向量的第i行、第j行,且线性相关;C′(i)、C′(j)为连通矩阵中元素更新后的第i行行向量、第j行行向量。
通过直接对连通矩阵C使用行扫描法,就可以进一步减少矩阵法的运算量,减轻存储压力,加快拓扑速度。
通过对网络进行全局拓扑辨识,可以将图1网络分为两个部分,在进行母线分析时,每一部分形成一条母线。第一部分是(节点1、2),编号为母线1号;另一部分是(节点3、4、5、6、7),编号为母线2号。在进行电气岛分析时,将变压器以及厂站之间的支路视为闭合支路,即可得到整个网络的连通模型,如图2所示。通过观察图2,发现母线1号、母线2号形成一个电气岛;然后返回到图1,可以知道:进线XL1,通过变压器向负荷4、5、6、7供电。

图2 正常的网络连通模型
2 考虑故障状态的局部拓扑辨识
在网络拓扑的过程中,网络中的支路断路器会因为各种各样的原因,如线路发生故障、断路器本身发生故障、调度员调度等,使得断路器状态发生变化。断路器状态发生变化后,可能会使之前的网络全局拓扑模型发生变化,一般情况下,为了保险起见,只能对整个网络再进行一次全局拓扑。但是,当网络中节点数目太多时,则全局拓扑的速度就会变慢,时效性就比较差。如果能围绕状态发生变化的断路器进行局部拓扑,那么就可以节省拓扑时间,加快拓扑速度。
在网络的拓扑中,每个电气岛中的母线分为一个或几个电压等级,不同电压等级的母线之间是不能通过断路器直接连接的。所以,当网络中某个断路器状态发生变化时,只会对断路器所处电压等级的母线的拓扑造成影响,而不会对不同电压等级的母线造成影响。也就是说,断路器状态发生变化对网络拓扑的影响只是局部的。基于这一点,可以在断路器状态发生变化时,只对网络进行局部拓扑,而不是全局拓扑。这样就可以进一步减少拓扑时间,提升拓扑效率。
2.1 局部拓扑关联矩阵的形成
2.1.1 对关联矩阵进行第1次节点消去
在全局拓扑中获得的关联矩阵,如式(2)所示。关联矩阵表示配电网系统中节点-支路的连接关系。根据节点消去法的目的,即将矩阵中不重要的节点消去,降低矩阵的阶数,减少运算量。而关联矩阵中也存在许多不重要的节点,需对其行向量进行节点消去处理。但是对关联矩阵进行节点消去时,对重要节点的定义与邻接矩阵不尽相同,还要加上母线节点,即关联矩阵中的重要节点包括:厂站之间的支路节点、变压器节点、供电电源节点、负荷节点以及母线节点。
对邻接矩阵进行消去时,图1中的重要节点为节点1—7,现在对关联矩阵进行节点消去时,重要节点还需增加节点8、节点9这两个母线节点,所以需要消去的节点为节点10、节点11。对关联矩阵进行第1次节点消去处理的公式为
A′(i)=[A(i)⊕A(j)]
(11)
式中:j为将要被消去的节点;i为被留下的重要节点;A(i)、A(j)为关联矩阵中行向量的第i行、第j行,且线性相关;A′(i)为关联矩阵中元素更新后的第i行行向量。
关联矩阵元素更新后,将矩阵的第j行进行删去处理。
所以,对关联矩阵进行第1次节点消去处理后,可以得到关联矩阵A′为

2.1.2 对关联矩阵进行第2次节点消去
当得到关联矩阵A′后,就可以对这个关联矩阵进行第2次节点消去,将矩阵中的母线节点消去,即将节点8、节点9进行消去处理。对关联矩阵进行第2次节点消去处理的公式为
A″(i)=[A′(i)+A′(j)]
(13)
式中:j为将要被消去的母线节点;i为被留下的重要节点;A′(i)、A′(j)为关联矩阵中行向量的第i行、第j行,且线性相关;A″(i)为关联矩阵中元素更新后的第i行行向量。
关联矩阵元素更新后,将矩阵的第j行进行删去处理。
所以,对关联矩阵进行第2次节点消去后,可以得到关联矩阵A″为

关联矩阵A″的行代表网络中的重要节点,列代表网络中的支路断路器。矩阵任意一列中,元素值不为0且相等的行,表示支路断路器与这些节点直接相连,以矩阵的第1列为例,断路器[1]处于关断状态时,节点1与节点2断开连接;矩阵任意一列中,元素值不为0且不相等的行,元素值最大的行表示与支路断路器直接相连的节点,以矩阵的第2列为例,断路器[2]处于关断状态时,节点3与节点4之间、节点3与节点7之间断开连接。
2.2 局部拓扑关联矩阵的使用
配电网系统中任意一个断路器都可能会因为各种各样的原因导致断路器状态发生改变,进而可能导致系统的拓扑发生变化,这时可以通过遥信获取故障断路器的信息,根据局部拓扑关联矩阵,针对变位断路器进行一次局部拓扑即可。
2.2.1 获取变位断路器信息
假设图1的网络出现异常情况,网络中断路器[3]、断路器[4]状态发生改变,从闭合状态变为关断状态,如图3所示。
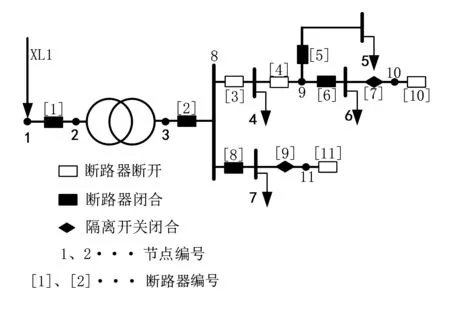
图3 异常的配电网台区网络
通过遥信获取的当前网络支路断路器状态矢量S′为
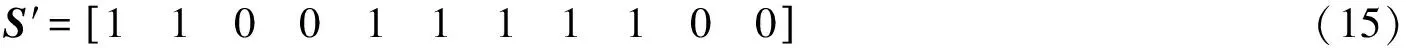
通过与初始支路断路器状态矢量S形成对比,很容易发现网络中的断路器[3]、断路器[4]状态发生变化。
2.2.2 获取变位断路器连接信息
当知道网络中断路器[3]、断路器[4]状态发生变化后,可通过局部拓扑关联矩阵A″,获取变位断路器的连接信息。
由变位断路器[3]对应矩阵的第3列,可知节点4与节点3之间、节点4与节点7之间断开连接;由变位断路器[4]对应矩阵的第4列,可知节点4与节点5之间、节点4与节点6之间断开连接。
2.2.3 对连通矩阵进行局部修改
当知道变位断路器的连接信息后,就可以根据所得到的信息,对连通矩阵C(如式(8)所示)进行局部修改,得到修改后的连通矩阵C′为

2.2.4 对连通矩阵直接进行矩阵行扫描
由于连通矩阵C′与全连通矩阵T′相同,所以直接对连通矩阵C′进行母线分析,可以将图3网络分为4部分。第1个部分为(节点1、2),编号为母线1号;第2部分为(节点3、7),编号为母线2号;第3部分为(节点4),编号为母线3号;第4部分为(节点5、6),编号为母线4号。进行电气岛分析,即可得到断路器[3]、断路器[4]状态发生变化的异常网络连通模型,如图4所示。通过观察图4,发现母线1号、母线2号形成一个电气岛,母线3号和母线4号分别形成一个电气岛;然后返回到图3,可以知道:进线XL1,通过变压器,向负荷7供电;负荷4连接的配电线路可能发生故障,所以被隔离开来,需要电力部门进行检修;负荷5、负荷6处于停电状态,调度员可以根据局部拓扑关联矩阵A″,对最近的联络开关(断路器[10])进行道闸操作,恢复供电,保证供电的可靠性。

图4 异常的网络连通模型

图5 配电网台区网络
通过局部拓扑辨识,可以发现网络中断路器状态发生变化,只会影响电压等级相等的母线,而不会影响到电压等级不相等的母线,所以,当网络中断路器状态发生变化时,对网络进行局部拓扑是可行的。通过局部拓扑来代替全局拓扑,可以大大提高网络拓扑的效率。
3 算例分析
如图5所示的配电网台区网络,该配电网台区网络中包含45个节点、47个断路器。首先,对该网络进行全局拓扑,全局拓扑流程如图6所示。
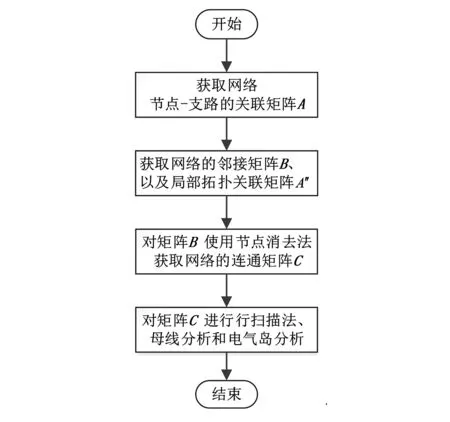
图6 全局拓扑流程
然后,将节点消去法的运算量与邻接矩阵法的运算量进行对比。其中邻接矩阵法在最坏的情况下需要进行(n-1)次自乘运算,所以对于图5中的网络,邻接矩阵法的最大运算量为4 009 500次。但是通过仿真可知,邻接矩阵法只需要进行20次自乘运算即可得到全连通矩阵,则邻接矩阵法的实际运算量为1 822 500次。图5中的网络,有13个重要节点,即节点1—13,所以利用节点消去法将其余的节点消去。
表1列出了针对图5的网络求取全连通矩阵所用方法的运算量。

表1 邻接矩阵法与节点消去法运算量的比较
表2列出了采用节点消去法所获得的连通矩阵C用不同的方法进行母线分析和电气岛分析的运算量。

表2 间接行扫描法与直接行扫描运算量的比较
表3列出了求取局部拓扑关联矩阵A″时,第1次节点消去以及第2次节点消去的运算量。针对图5网络,第1次节点消去需要将除重要节点1—13以及母线节点18和母线节点23之外的节点消去;第2次节点消去再将母线节点18、母线节点23消去。

表3 关联矩阵节点消去法运算量
全局拓扑完毕后,针对网络中状态发生变化的断路器进行局部拓扑,局部拓扑的流程如图7所示。

图7 局部拓扑流程
表4列出了针对图5网络中断路器状态发生变化时,进行全局拓扑、局部拓扑仿真得到准确结果所用的时间。

表4 全局拓扑与局部拓扑的仿真时间
通过仿真结果,节点消去法相对于邻接矩阵法,可以减少许多的运算量;直接对连通矩阵使用行扫描法是可行的,相对于连通矩阵自乘获取全连通矩阵再进行行扫描来说,也可以减少一定的运算量;针对图5中的网络使用局部拓扑所用的时间是全局拓扑的1/3左右,使拓扑的效率更高了。
4 结 语
对配电网台区用矩阵法进行拓扑辨识,针对矩阵法拓扑辨识存在的运算量大、拓扑效率低的问题,提出了解决方案。通过全局拓扑、局部拓扑两个方面来解决这些问题。针对以往全局拓扑中最耗时的邻接矩阵法,选择用节点消去法来替代;然后,对从全连通矩阵到行扫描法、母线分析和电气岛分析的过程进行简化;最后,针对关联矩阵进行两次节点消去,获取局部拓扑关联矩阵,大大减小了全局拓扑运算量。全局拓扑后,在网络中断路器状态发生变化时,对断路器进行局部拓扑,虽然仿真结果显示局部拓扑用时是全局拓扑的1/3左右,效果并不算特别好,这是由于所选网络节点数少以及网络结构简单所导致的。如果选用节点数多、结构复杂的网络,则全局拓扑时间会大大加长,这时,局部拓扑的优势就能体现出来了。
