基于一维卷积神经网络的电力系统暂态稳定在线评估

齐 放

(中国广核新能源控股有限公司, 北京 100000)

0 引 言

近年来，由于暂态失稳所引发的电力系统事故时有发生，对社会和经济产生极大的危害。然而，传统电力系统暂态稳定计算基于时域仿真，包含复杂的微分代数方程，在大电网中计算复杂，难以进行暂态稳定在线评估与风险预警[1-4]。

近年来，机器学习技术被引入电力系统暂态稳定评估中，通过非线性方程替代复杂微分代数方程计算，加速暂态稳定评估速度，以满足在线应用需求。文献[5]提出了暂态稳定安全域的概念，并在安全域下提出基于多支持向量机的综合电力系统暂态稳定评估方法，可减少暂态失稳场景的误判。文献[6]中离线数据通过相量测量单元PMU采集得到，并通过串行集成多棵回归树构建基于XGBoost的暂态稳定预测模型，实现暂态稳定特征重要度排序关系，提高了模型的可解释性。文献[7]将概率神经网络和径向基函数神经网络结合，形成复合神经网络，并用于故障临界切除时间裕度的预测，提升预测精度。文献[8] 将深度置信网络作为黑盒模型拟合发电机出力和系统暂态稳定系数间映射关系，实现暂态稳定评估。文献[9]直接基于底层数据，将堆叠自动编码器引入电力系统暂态稳定评估中，采用“预训练-参数微调”的两阶段学习方法和稀疏化技术提升暂态稳定评估准确度。

下面提出一种基于一维卷积神经网络(one dimensional convolutional neural network, 1DCNN)的电力系统暂态稳定在线评估方法，将在图像学习中广泛应用的卷积神经网络(convolutional neural network, CNN)引入电力系统暂态稳定评估中，相较于传统神经网络方法，有更强的抽象拟合能力，并且1DCNN是传统CNN的一维形式，更适合电力系统数据的学习。

1 样本生成

1.1 马尔可夫链蒙特卡洛抽样

马尔可夫链是一个序列模型，其中数据样本之间存在依赖关系，且时刻t的状态概率只与前一时刻t-1的状态有关。在马尔可夫链中有状态转移矩阵，状态概率矩阵本身通过一定次数的矩阵乘法后，转移矩阵每一行的概率会趋向于稳定的值，称为马尔可夫链的平稳分布，即[10-12]：

P(xt∣xt-1,xt-2,…,x1)=P(xt∣xt-1)

(1)

(2)

式中：P为状态转移矩阵；x为样本；π为平稳概率分布；n为转移次数，当接近无穷时，P接近π，即达到平稳分布。

马尔可夫链蒙特卡洛抽样算法(Markov chain Monte carlo sampling algorithm，MCMC)是马尔可夫链和蒙特卡洛抽样的结合。设给定的初始样本为x0，根据马尔可夫链的收敛性质，经过一定次数的矩阵连乘后，x的采样概率都会收敛到一个平稳分布，设为π(x)，则后续所有样本均服从概率分布π(x)。MCMC是从xn+1开始的采样(设n为矩阵连乘次数)：

(3)

式中，x*为新样本。πt+1(x*)和πt+1(x)同分布。

实际中采用经典的MCMC采样的Metropolis Hasting算法进行采样：

1)初始化：初始化t0时刻样本为x0，所需抽样的样本总数为M。

2)循环：

(1)从均匀分布U(0, 1)中采样u；

(2)从概率分布q(x*|xi)中采样样本x*；

则xi+1=x*，否则xi+1=xi；

(4)当所生成样本数达到M，结束循环。

3)结束：得到基于MCMC采样的Metropolis Hasting算法采样结果。

1.2 基于MCMC的电力系统运行数据生成

电力系统包括PV节点、PQ节点和Vθ节点，以电力系统潮流计算和时域仿真计算的初始参数为所需抽样的特征参数，因此所考虑的电力系统特征包括：发电机有功出力、发电机节点电压、有功负荷和无功负荷。根据所研究电力系统模型的特征，设置各个特征变量的取值范围，然后通过MCMC抽样算法抽样海量的电力系统运行数据。基于MCMC的抽样结果可以使电力系统特征在取值范围内分布更加均匀，增加样本的代表性，有助于提高1DCNN模型的泛化性能。

根据以往经验，对系统模型设置短路类型、故障位置以及故障切除时间，并执行时域仿真计算，得到对应的发电机最大功角差。最大功角差超出180°即视为失稳，否则认为系统稳定。若故障数量为N，则单个电力系统运行数据包括N个最大功角差，分别对应不同的故障[13]。

2 基于1DCNN的暂态稳定评估

2.1 一维卷积神经网络

CNN是一种前馈神经网络，它的人工神经元可以对一定覆盖范围内的输入特征进行响应，在大型图像处理中性能突出。CNN由一个或多个卷积层、线性整流层、池化层和顶端的全连通层组成。1DCNN是CNN的一维形式，被普遍应用于序列数据识别中，更适合电力系统状态特征向量的识别，相比于传统神经网络方法，具有更高的拟合准确度和更好的泛化性能等优点[14-16]。

1)输入层

CNN的输入层用于接收输入数据，其中1DCNN的输入层的输入参数为一维数据，在这里为发电机有功出力、发电机节点电压、有功负荷和无功负荷组成的向量。

2)卷积层

卷积层的功能是对输入数据进行特征提取，内部包含多个卷积核，并且含有权重和偏置需要进行训练更新。卷积核比输入参数维度小，对于1DCNN，卷积核也为一维，并且会在输入参数上进行滑动，对其范围内参数进行特征提取和映射，并且需要设置每次滑动步长。

3)激活函数

对卷积层得到的特征进行非线性化处理，增加模型的拟合能力，常用的激活函数有ReLU、Sigmoid等。

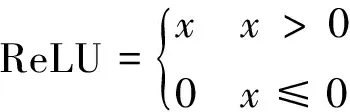
(4)

(5)

式中，x为激活函数的输入。

所选用的激活函数为ReLU函数，如图1所示。

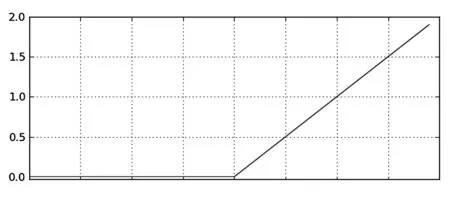
图1 RuLU函数

4)池化层

池化层的作用是对数据进行降维，其会设定池化区域，在该区域内进行降维，常用的池化操作有：

(1)最大值池化：在池化区域内取最大值作为最终的特征。

(2)平均值池化：在池化区域内取均值作为最终的特征。

设滑动步长为2，卷积核长度为4，对长度为9的向量卷积结果如图2所示。

图2 最大值池化和平均值池化

5)全连接层

CNN中的全连接层等价于传统前馈神经网络中的隐含层，包括前向传播和反向传播两部分。

前向传播中，数据从输入到输出，第l层的输出为

al=σ(zl)=σ(Wlal-1+bl)

(6)

式中：σ为激活函数；Wl为权重，bl为偏置；zl为未激活前输出；al为输出。

反向传播由输出向输入传播，并逐层更新权重和偏置，更新的依据为1DCNN的正向输出结果和时域仿真计算结果的偏差，偏差的表达式为

(7)

式中：x为样本输入；y为样本真值；J为偏差。

J对W和b求梯度为：

得到梯度后，使用随机梯度下降法更新W和b，减小偏差。

6)输出层

输出层为CNN的最终输出结果，1DCNN的最终输出结果为所有故障的最大功角差。

除此之外，在训练1DCNN的过程中使用了L2正则化仿真过拟合：

(10)

式中，λ为L2正则化的超参数。

1DCNN在Tensorflow框架上进行搭建，搭建好的1DCNN的模型如图3所示。

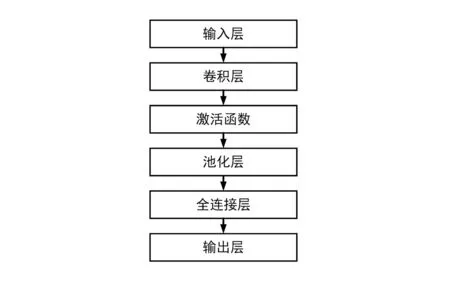
图3 1DCNN结果

2.2 基于1DCNN的暂态稳定评估

1DCNN模型搭建好之后，将MCMC产生的运行场景(发电机有功出力、发电机节点电压、有功负荷和无功负荷)作为1DCNN的输入参数，将所有故障的最大功角差作为输出参数，并对1DCNN进行训练，所提1DCNN结构如图4所示。

图4 1DCNN结构

以发电机最大功角差是否超过180°作为判断系统是否失稳的标准，并且只要有一个故障下的最大功角差超过180°，即认为系统失稳。因此准确度定义为1DCNN模型成功判断系统稳定性的百分比。

3 算例分析

3.1 测试系统

选取新英格兰10机39节点系统进行算例测试，该系统包括39个节点、10台火力发电机、34条输电线路、12台两绕组变压器和19个负荷，该系统的示意图如图5所示[17]。

图5 新英格兰10机39节点系统

3.2 电力系统运行数据仿真

设置发电机有功出力在基础出力的80%～120%、发电机节点电压的标幺值在0.95～1.1、有功负荷和无功负荷均在80%～120%之间波动。通过MCMC算法抽样5000个样本，作为电力系统运行场景。

设置39节点系统的故障类型为输电线路三相短路故障，故障位置为线路中心，故障数量为15条输电线路，故障持续时间为0.5 s，在电力系统工具箱PST中进行时域仿真计算，得到不同故障下发电机的最大功角差，将其与对应的运行场景结合，作为训练1DCNN的样本数据。

3.3 基于1DCNN的暂态稳定评估结果

样本数据生成后，对1DCNN模型进行训练，将MCMC产生的运行场景(发电机有功出力、发电机节点电压、有功负荷和无功负荷)作为1DCNN的输入参数，输入参数的维度为58；将所有故障的最大功角差作为输出参数，输出参数的维度为15。设置输入层、卷积层、激活函数、池化层、全连接层和输出层数量各为1，共6层。设置每批次训练样本数量为500，训练次数为100，训练集数量为4000，测试集数量为1000，对1DCNN进行训练，其在训练过程中的误差曲线如图6所示。

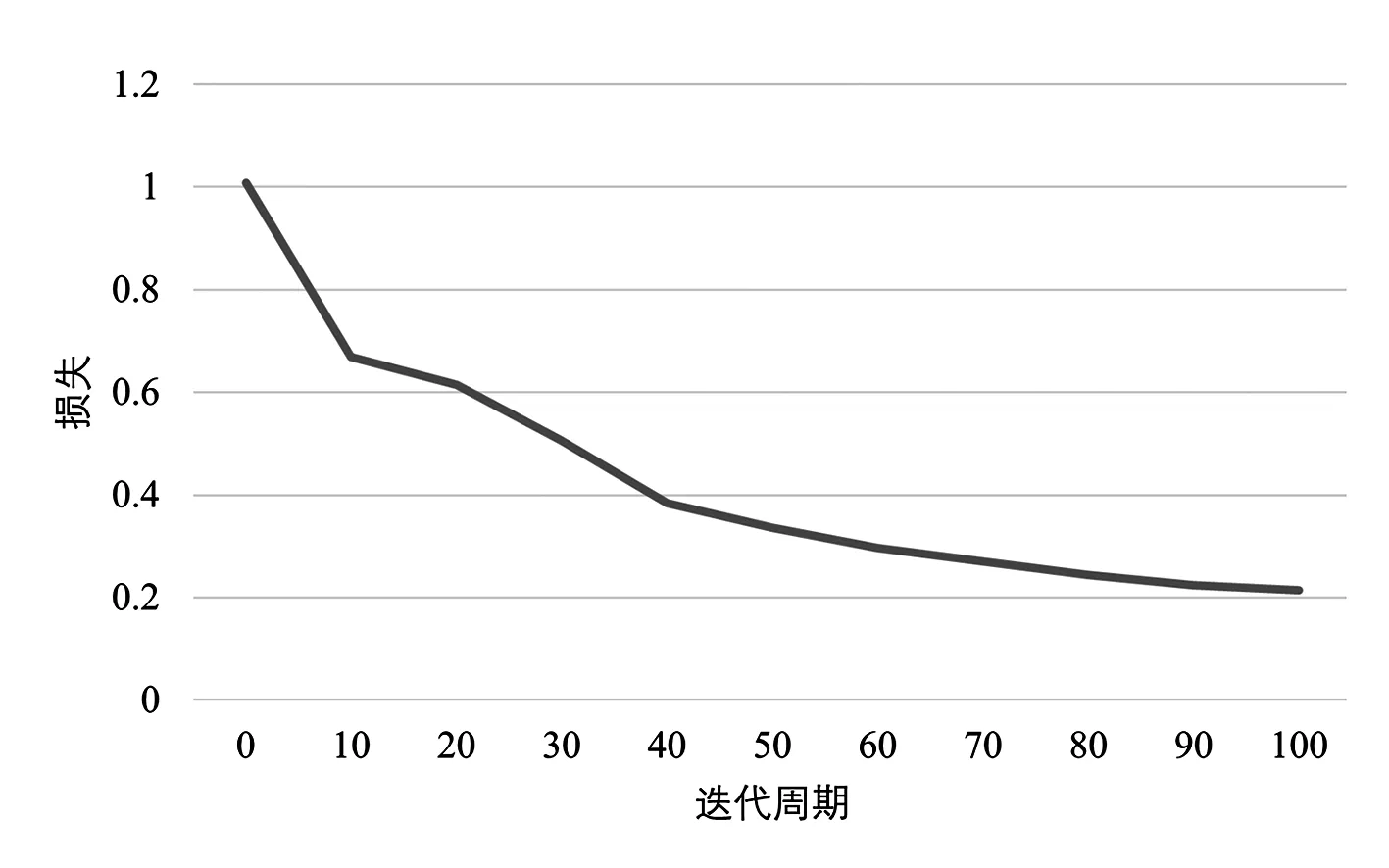
图6 训练集损失曲线

从图6可以看出，随着训练迭代次数增加，损失逐渐降低，表明1DCNN实现了基于运行场景的暂态稳定拟合。

1DCNN的准确率如图7所示。由图7可以看出，随着迭代周期的增加，1DCNN的准确度持续增加，并且在末端保持在90%以上的准确度，表明所提算法实现了暂态稳定的准确评估。

图7 训练集准确率曲线

训练好1DCNN模型后，可进行在线的暂态稳定评估，与传统基于时域仿真的暂态稳定评估相比，在评估速度上得到极大提升，评估时间对比如表1所示。

表1 算法评估时间对比单位：s

从表2可以看出基于1DCNN的暂态稳定评估算法在计算时间上相较于传统时域仿真方法有极大提升，并且可以同时得到所有故障的暂态稳定评估结果，故障数量越多，算法在评估时间上的优势越明显。

最后，对比所提方法与其他文献方法的评估准确度，结果如表2所示。

表2 评估准确度对比

从表2可以看出所提方法在准确度上明显优于其他方法，可以实现更加精准的电力系统暂态稳定评估。

4 结 语

上面提出了一种基于1DCNN的电力系统暂态稳定在线评估算法。该算法将1DCNN引入电力系统暂态稳定评估和安全风险辨识中，通过MCMC算法生成算例模型海量可能的运行场景，并通过时域仿真计算暂态稳定指标，通过1DCNN实现暂态稳定性能快速评估。并在新英格兰10机39节点系统中进行了算例验证，算例结果表明了所提算法的可行性和先进性。通过算例分析，得到如下结论：

1)利用马尔科夫链和蒙特卡洛抽样算法结合的MCMC算法对电力系统运行场景进行抽样，所生成样本可以很好反映系统运行特征，提高1DCNN的泛化性能；

2)将1DCNN引入电力系统暂态稳定评估中，将系统运行场景作为输入参数，将所有故障的最大功角差作为输出，对1DCNN进行训练，实现了基于1DCNN的电力系统暂态稳定快速评估，并且从算例结果可以看出所提算法评估时间满足在线应用的需求。