换流站导体载流量计算方法比较与研究

韩毅博，马 亮，王 刚

(中国电力工程顾问集团中南电力设计院有限公司，湖北 武汉 430071)

0 引 言

导体载流量计算是直流换流站设计的重要组成部分。目前，国内直流换流站导体选择设计时，一般采用电气设计手册中的公式[1]计算或直接引用现行DL/T 5222—2005《导体和电器选择设计技术规定》[2]附录中的有关结果。然而，直流换流站导体承受的电流应力较为复杂：直流侧导体主要承载较小谐波的直流电流；阀厅及交/直流滤波器的部分导体承载谐波含量十分丰富的交流电流或带纹波的直流电流。上述公式及规范均仅针对导体流过常规交流电流时的工况分析，并不完全适用于直流换流站中导体载流量的计算。因此，有必要开展换流站导体载流量计算方法的比较与研究，确定合适的计算方法。

1 换流站导体载流量计算原理分析

1.1 换流站导体载流量热平衡方程的修正

同交流导体类似，直流换流站中导体载流量计算的基本物理学原理同样基于热平衡方程，即导体的总散热量同总发热量相等。

空气中导体的散热途径主要包括对流散热、辐射散热和传导散热，发热来源包括焦耳热和太阳辐射吸热。考虑上述各方面因素，IEEE 605—2008给出交流导体热平衡方程可用式(1)表示[3]。

I2RF+qs=qc+qr+qcond

(1)

式中：I为流过导体的电流，A；R为一定温度下单位长度导体直流电阻，Ω/m；F为集肤效应系数；qs为太阳辐射吸热功率，W/m；qc为对流散热功率，W/m；qr为辐射散热功率，W/m；qcond为传导散热功率，W/m，一般忽略不计。

对于直流换流站中的导体，由于其承受电流应力较为复杂，故应将式(1)中导体电流热效应扩充至适用于换流站导体实际电流应力的情况。

根据叠加原理，考虑不同频率谐波集肤效应的损耗因数，含谐波的工作电流流过导体产生的焦耳热功率按式(2)计算。

式中：k为谐波次数；Ik为k次谐波电流；Rack为k次谐波电流下导体的交流电阻。

集肤效应引起的损耗因数Ys由式(3)计算。

其中：

式中：D为钢芯铝绞线外径，cm；Ds为钢芯绞线外径，cm；Rd为导体的直流电阻。

考虑集肤效应的k次谐波电流下导体的交流电阻Rack为

Rack=(1+Ys-k)Rd

(7)

式中，Ys-k为k次谐波下的导体集肤效应损耗因数。

这样，换流站单导体载流量计算的热平衡方程由式(1)修正为

对于多分裂导线及钢芯铝绞线，还需分别考虑邻近效应和钢芯磁化损耗的影响，其热平衡方程表示为

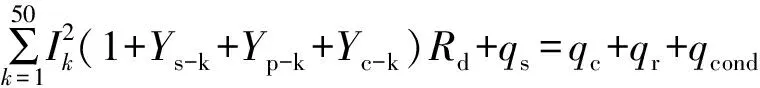
(9)

式中：Yp-k为k次谐波下的导体临近效应损耗因数；Yc-k为k次谐波下的钢芯铝绞线磁化损耗因数。集肤效应和磁化损耗因数的计算详见文献[2]。

1.2 换流站导体载流量计算实例

对于谐波含量极少的换流站直流导体，其载流量、热效应计算相比交流导体更为简单，计算时仅将交流电阻改为直流电阻即可，故本节不再赘述。这里主要针对换流站中部分除流过正常工作电流外，还流过可观谐波电流的导体，计算其谐波电流的热效应。以某±800 kV/10 000 MW直流换流站换流变压器阀侧为例，其电流谐波频谱如表1所示。

由表1可以看出，换流变压器阀侧的导体除流过正常工作电流外，还流过可观的谐波电流。计算导体载流量时，一方面需确定考虑谐波的导体电阻损耗；另一方面考察不同次数谐波电流作用下集肤效应系数的区别。

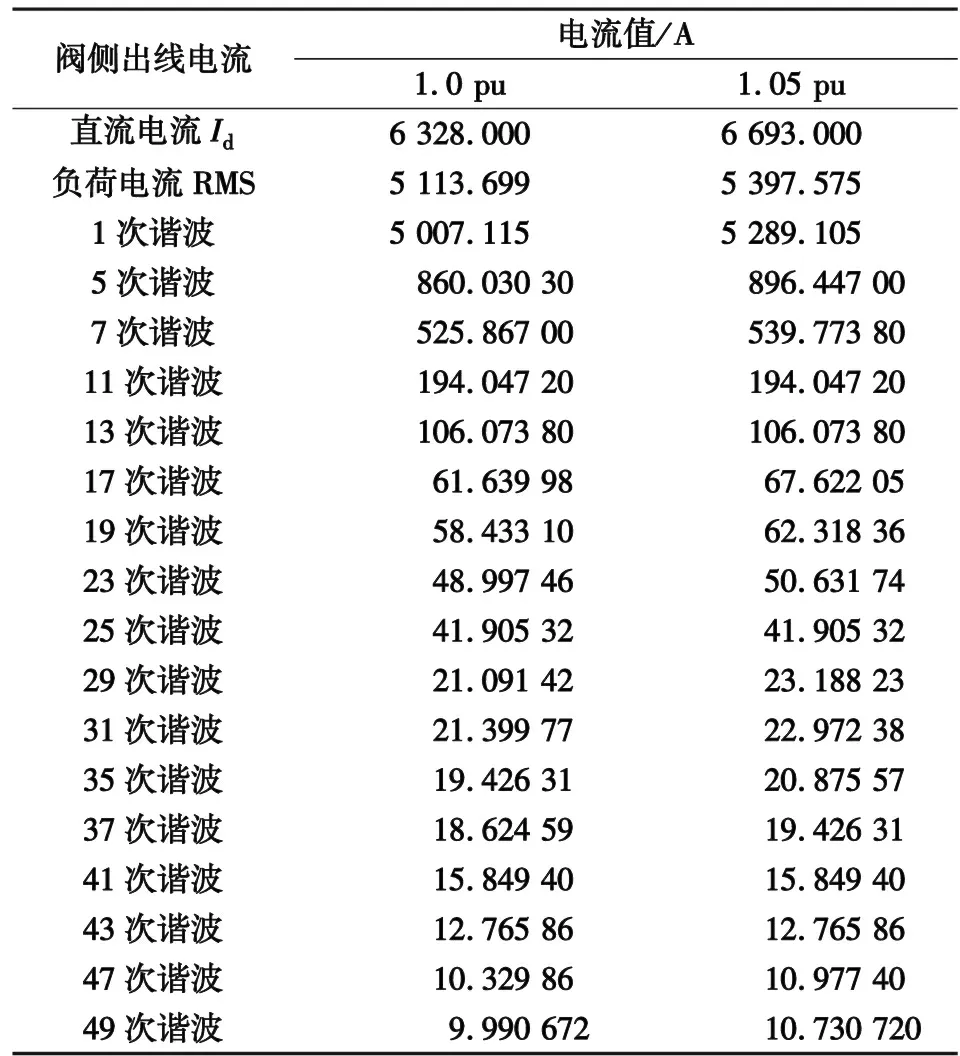
表1 某±800 kV/10 000 MW直流换流站换流变压器阀侧出线谐波电流频谱

以直流换流站阀厅内常用的LJ-1120纯铝绞线为例，计算得到1.05 pu下各次频率谐波电流的集肤效应损耗因数及其焦耳热，如表2所示。

由表2可以看出，对于换流变压器阀侧的LJ-1120纯铝绞线，考虑谐波后全电流产生的焦耳热功率比基波载流量焦耳热功率高约7.1%；此外，对于换流变压器阀侧，5、7次谐波贡献的焦耳热占所有5～49次谐波焦耳热总和的94%。上述结果表明，谐波电流热效应在换流站导体载流量计算中是不可忽略的，而具有较高幅值的低次谐波电流的热效应是导体选择中需要重点考虑的对象。

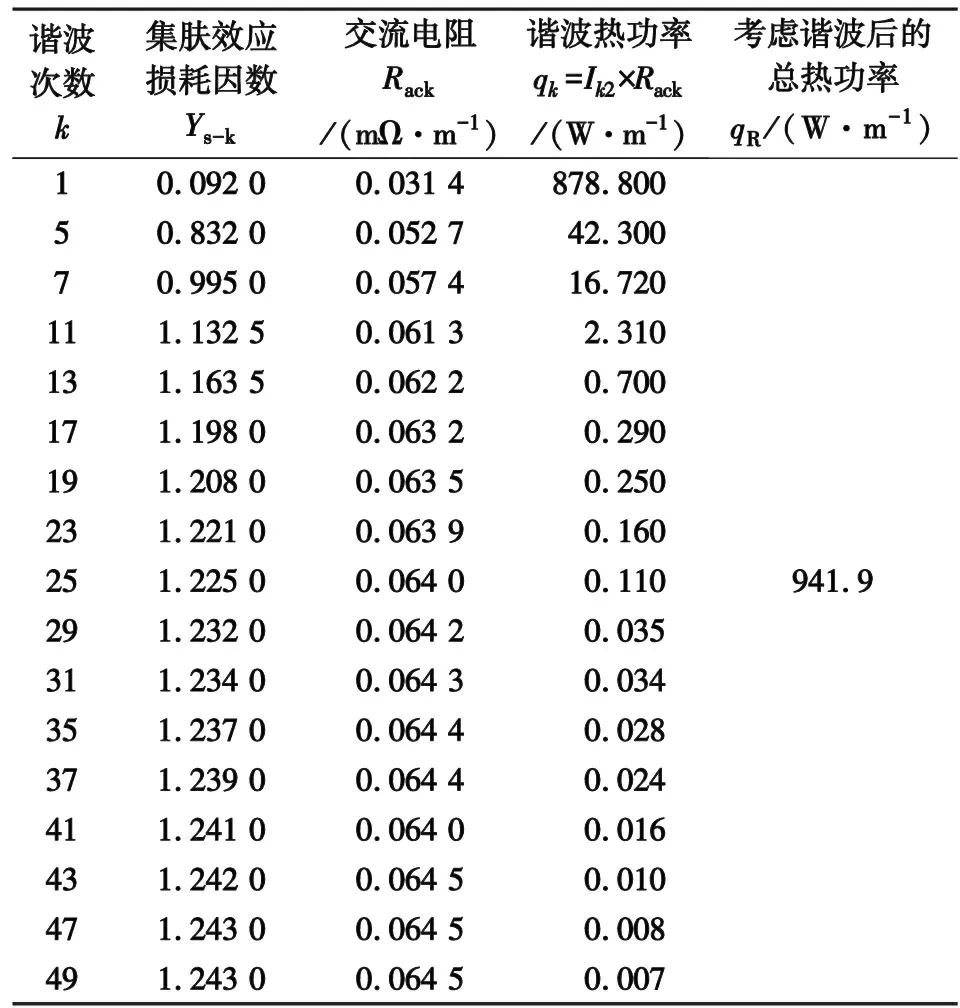
表2 考虑谐波的换流变压器阀侧LJ-1120焦耳热功率

2 换流站导体载流量计算方法研究

国内工程交流导体载流量一般根据DL/T 5222—2005附录中的数值选取。在某些涉外工程中，业主提出应根据后续发布的IEEE 738—2006(2012)或IEEE 605—2008等规范进行较为详细的载流量计算，而其计算原理与DL/T 5222—2005及电气一次手册不尽相同。文献[9]对比了IEC 61957—1995[5]和IEEE 738—2006[6]的载流量计算方法，根据不同方法的计算结果，提出了不同环境条件下建议采用的方法，但未将电气一次手册解析计算法及DL/T 5222—2005载流量计算方法纳入比较。下面从计算原理出发，结合工程设计实际需求，对比国内外5种载流量计算方法，探讨适用于换流站导体载流量计算的方法。

2.1 导体载流量计算的几种方法

2.1.1 导体直流电阻R的计算方法

各规范规定的一定温度下单位长度导体直流电阻R计算方法相同，按式(10)计算。

R=R20[1+α20(θ-20)]

(10)

式中：R20为20 ℃时导体直流电阻，Ω/m；α20为导体电阻温度系数；θ为导体最高允许温度，℃。R20可根据导体样本给出的数值选择，或根据导体截面积及材料电阻率计算得到。

2.1.2 对流散热功率qc的计算方法

根据传热学基本原理，根据流动起因的不同，对流散热可以区别为强制对流散热和自然对流散热。前者是由于外部动力源造成的，而后者通常是由于流体内部的密度差所引起。两种流动的成因不同，流体中的速度场也有差别，换热规律不一样。因此，对流散热功率qc包括强迫对流散热功率qcf和自然对流散热功率qcn。根据调研，现有文献对以上两个参数的计算方法不尽相同，具体情况如下。

1) 《电气一次设计手册》相关计算方法

《电气一次设计手册》给出了导体对流散热功率计算方法，对于软导线的强迫对流散热功率，风袭角取90°，按式(11)计算。

qcf=0.57πλfΔtRe0.485

(11)

式中：λf为导线表面空气层的传热系数，W/(m·℃)；Re为雷诺数。

Re=VD/vf

(12)

式中：V为垂直于导线的风速，m/s；D为圆柱形导体外径，m；vf为导线表面空气层的动态粘度，m2/s。

vf=1.32×10-5+9.6(θa+θ/2)×10-8

(13)

式中，θa为环境温度，℃。

上述方法主要用于有风条件下计算软导线的对流散热功率，计算了其中强迫对流散热的部分。但对于室内的无风或微风情况，自然对流散热效应占主导地位，《电气一次设计手册》并未涉及这一方面。此外，上述计算方法并未直接体现海拔的影响。

2)DL/T 5222—2005 《导体和电器选择设计技术规定》采用的载流量计算方法

DL/T 5222—2005中附录A给出的各型号导体载流量结果最早见于文献[7]，以式(14)描述对流散热功率Qc为

Qc=α1(tm-t0)F1(W/m)

(14)

式中：αl为对流换热系数，W/(m2·°C)；tm为导体运行温度，℃；t0为周围空气温度，℃；Fl为单位长度对流换热面积，m2/m。

由于对流条件不同，分为自然对流和强迫对流两种情况。屋内自然通风或屋外风速小于0.2 m/s，属于自然对流换热。空气自然对流换热系数，可按大空间湍流(又称紊流)状态来考虑，自然对流换热系数按式(15)计算。

α1-natural=1.5(tm-t0)0.35

(15)

对圆管导体，有

F1=πD

(16)

屋外配电装置中的管形导体，常受到大气中风吹的作用，风速越大，空气分子与导体表面接触的数目增多，对流换热的条件就越好，形成强迫对流换热。强迫对流换热系数αl-force为

式中：λ为空气的导热系数，当气温为25 ℃时，λ=2.55×10-2W/(m·℃)；D为圆管外径，m；Nu为努塞尔数，其值为

式中：V为风速，m/s；v为空气的运动粘度系数，当气温为25 ℃时，v=16.16×10-6m2/s。

根据上述方法，户内导体按自然对流散热原理计算，户外导体按强迫对流散热原理计算。此外，上述计算方法仍未直接体现海拔的影响，而是通过海拔修正系数对标准环境条件下的计算结果进行修正。该方法公式虽同《电气一次设计手册》形式不同，但计算结果及原理基本一样，以下将两者作为同一种方法介绍。

3) IEEE 605—2008相关计算方法

IEEE 605—2008 IEEE气体敞开式绝缘变电站母线设计导则(IEEE Guide for Bus Design in Air Insulated Substations)提出强迫对流散热功率按式(19)计算。

(19)

式中：ka为导线表面空气层的传热系数，W/(m·℃)；L为导体直径，m；Pr为空气的普朗特数，取0.7；A为单位长度导体的迎风面积，m2/m；ΔT为导体最高允许温度Tc和周围空气温度Ta之差，°C；Re为雷诺数。

ka与导体表面空气膜温度有关，按式(20)计算

式中，Tfilm为导体表面空气膜温度，等于导体最高允许温度Tc和周围空气温度Ta的平均值。

IEEE 605—2008 给出的雷诺数计算方法同《电气一次设计手册》的式(12)有所区别，雷诺数Re为

式中：ρf为空气绝对密度，kg/m3；μf为空气动力粘度，kg/(m·s)。

不同温度及海拔条件下，ρf按式(23)计算。

式中，H为海拔高度，m。

μf取值同温度有关：

IEEE 605—2008提出，对于无风或多导体近距离平行排布的情况，应计算自然对流散热功率。对于水平圆柱体自然对流散热，其引用了IEEE 738—2006的公式，计算风速为0时的自然对流功率，如式(25)所示(风袭角取90°)。

4) IEEE 738—2012相关计算方法

IEEE 738—2012 IEEE计算架空裸导体电流-温度特性的规范(IEEE Standard for Calculating the Current-Temperature of Bare Overhead Conductors)指出，式(26)适用于低风速，式(27)适用于大风速，强迫对流散热功率取式(26)和式(27)的最大值(风袭角取90°)。

式(26)、式(27)和IEEE 738—2006中的表达式是等价的，但IEEE 738—2012明确其适用的导体外径范围为20～150 mm。

对于自然对流散热功率，按式(28)计算。

5) IEC 61597相关计算方法

IEC 61597(Overhead electrical conductors-calculation methods for stranded bare conductors)仅考虑强迫对流散热，其中强迫对流散热功率按式(29)计算。

qcf=λfNu(Tc-Ta)π

(29)

式(29)中部分物理量取值同前述方法不同：λf为导体表面空气膜热导率，IEC 61597规范规定其取常数0.025 85 W/(m·K)。

Nu为努塞尔数，按式(30)计算。

Nu=0.65Re0.2+0.23Re0.61

(30)

Re为雷诺数，按式(31)计算。

(31)

式中：v为风速，m/s；D为导体直径，m；Tc为导体最高允许温度，K；Ta为周围空气温度，K。

2.1.3 辐射散热功率qr的计算方法

IEEE 605—2008及《电气一次设计手册》均采用式(32)所示的斯蒂芬-玻尔兹曼方程计算导体的辐射散热功率。

qr=5.669 7×10-8×επD[(Tc+273)4-(Ta+273)4]

(32)

式中：qr为辐射散热功率，W/m；ε为辐射散热/吸热系数(黑度系数)。ε取值详见表3，对于换流站内的管型母线，ε=0.5；对于换流站内长期运行的铝绞线，可以认为其表面氧化变黑，ε=0.9。

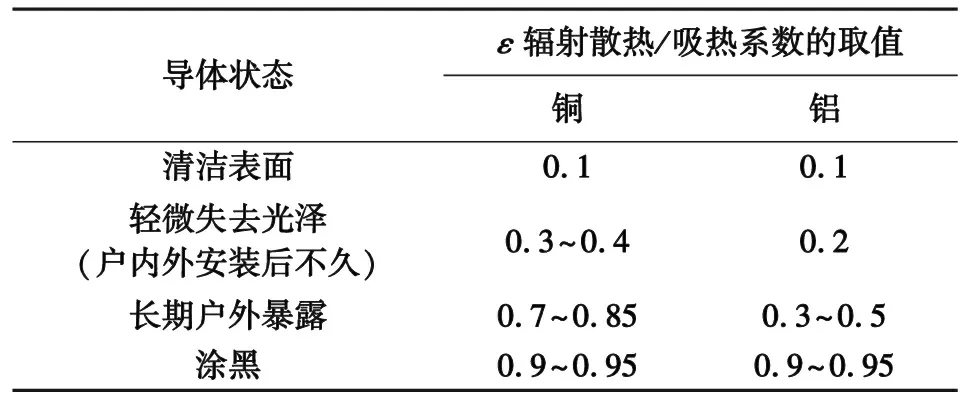
表3 典型导体表面辐射散热/吸热系数

2.1.4 太阳辐射吸热功率qs的计算方法

根据IEEE 605—2008，太阳辐射吸热功率qs按式(33)计算。

qs=εQsA′Ksinφ

(33)

式中：qs为太阳辐射吸热功率，W/ m；ε为辐射吸热系数，取值同表3；φ为太阳辐射角，保守考虑时可取90°；A′ 为单位长度导体垂直于太阳辐射的投影面积，对于圆柱型导体其A′=πD，m2/m；Qs为太阳辐射强度, W/m2；K为海拔辐射修正系数，IEEE 738-2012给出其计算公式为

K=1+1.148×10-4H-1.108×10-8H2

(34)

需要指出的是，IEEE还给出了导线所处纬度、季节、时间、环境、高度、走向等不同因素下的太阳辐射吸热功率计算方法。针对工程设计应用的实际情况，这里仅计算其最严格条件下的数值。

2.2 导体外表面对流散热原理分析及计算方法

从第2.1节可以看出，在热平衡方程中，各规程规范或手册中关于导体对流散热的计算公式不尽相同：一些明确区分了强迫对流散热和自然对流散热；一些仅考虑了强迫对流散热。在强迫对流散热方面，计算公式也不尽相同，因此，对流散热原理进行简要分析，从工程应用和传热原理两方面出发，讨论选择相应合适的计算方法。

2.2.1 强迫对流散热计算结果分析

采用第2.1节对应的不同公式，分别计算导体在海拔为0 m和1000 m时的强迫对流散热功率。基本计算条件为：环境温度25 ℃，导体最高允许温度80 ℃，风速0.5m/s。海拔为0 m的计算结果如图1所示(在这一条件下，《电气一次设计手册》计算结果和DL/T 5222—2005计算结果一致，下同)。可以看出，对于外径60～400 mm范围内的导体，采用《电气一次设计手册》计算得到的强迫对流散热功率最小，即最保守。然而，《电气一次设计手册》相关计算方法并未给出海拔影响，需对其进行修正，以计算不同海拔条件下的载流量。

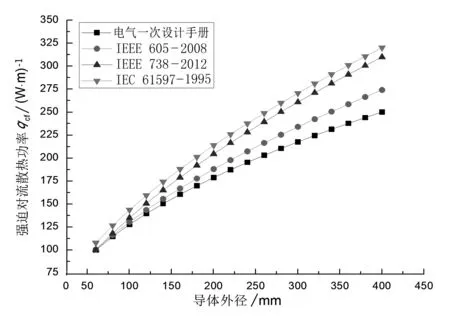
图1 不同计算方法得到的导体强迫对流散热功率(海拔0 m)

根据传热学基本原理，容易知道海拔对强迫对流散热的影响主要体现在海拔升高、空气密度下降、强迫对流散热效应减弱。《电气一次设计手册》及DL/T 5222—2005相关计算方法中，雷诺数的计算应考虑海拔修正，其计算公式应修正为式(35)，即

空气密度随着海拔高度的改变而改变，但是特定模型特定区域的尺寸和流速是不变的。参照文献[8-9]，根据空气密度与海拔的关系，可以得到Re的海拔修正公式为

Re(H)=η(H)Re(0)

(36)

式中：Re(H)为海拔H处的雷诺数；η(H)为海拔为H处的空气相对密度，表达式为

η(H)=(1-2.255 77×10-5H)5.255 9

(37)

上述雷诺数Re的海拔修正方法，和IEEE 738—2012中空气绝对密度ρf和空气动力粘度μf关于海拔H的关系式是等价的，可以得到相同的修正结果。

采用上述修正后的《电气一次设计手册》计算方法，计算海拔为1000 m的不同直径导体的强迫对流散热功率，结果如图2所示。综合图1和图2可以看出，采用未修正的《电气一次设计手册》及IEC 61597—1995方法计算的强迫对流散热功率并没有随着海拔增加而变化；而IEEE 605—2008及IEEE 738—2012方法计算的高海拔下强迫对流散热功率明显下降；采用修正后《电气一次设计手册》计算方法得到的强迫对流散热功率同样随海拔增加而下降。

图2 不同计算方法得到的导体强迫对流散热功率(海拔1000 m)

从计算结果看，海拔为0 m时，各种方法计算的强迫对流散热功率计算值大小有“IEC 61597—1995”>“IEEE 738—2012”>“IEEE 605—2008”>“电气一次设计手册”的关系；考虑海拔修正时，有“IEEE 738—2012”>“IEEE 605—2008”>“电气一次设计手册(修正)”的关系。IEC 61597—1995主要针对输电线路，其散热环境好于变电站、换流站内，故其散热功率计算值最大，计算得到的导体载流量也最大，有利于最大程度地利用导体载流面积，提升输电线路的经济性。而修正电气一次设计手册计算方法得到的散热功率最小，计算得到的导体载流量也最小。因此，对于换流站内的户外导体，若保守考虑，工程中可采用修正的《电气一次设计手册》的方法计算导体的强迫对流散热功率，具有足够的裕度。

2.2.2 自然对流散热计算结果分析

根据第2.1节内容，对于换流站户内导体，由于一般没有均匀风速的空气流动，没有强迫对流散热过程，应采用自然对流散热原理计算其对流散热功率。分别采用不同方法计算了导体的自然对流散热功率，如图3所示，虽然IEEE 605—2008在IEEE 738—2012给出的公式基础上将系数四舍五入、向上取整，但方法是统一的，其散热功率随外径增加而增加的趋势是一致的。根据DL/T 5222—2005的计算结果，热源向周围传递的热量与导体外径成正比，同IEEE计算结果相比存在一处转折点：当导体外径小于100 mm时，DL/T 5222—2005的自然对流换热功率计算结果比IEEE小，当导体外径大于100 mm时，DL/T 5222—2005的自然对流换热功率计算结果比IEEE计算结果大，且差值逐渐增加。实际工程中，可根据导体的外形尺寸，选择相对保守的计算方法。

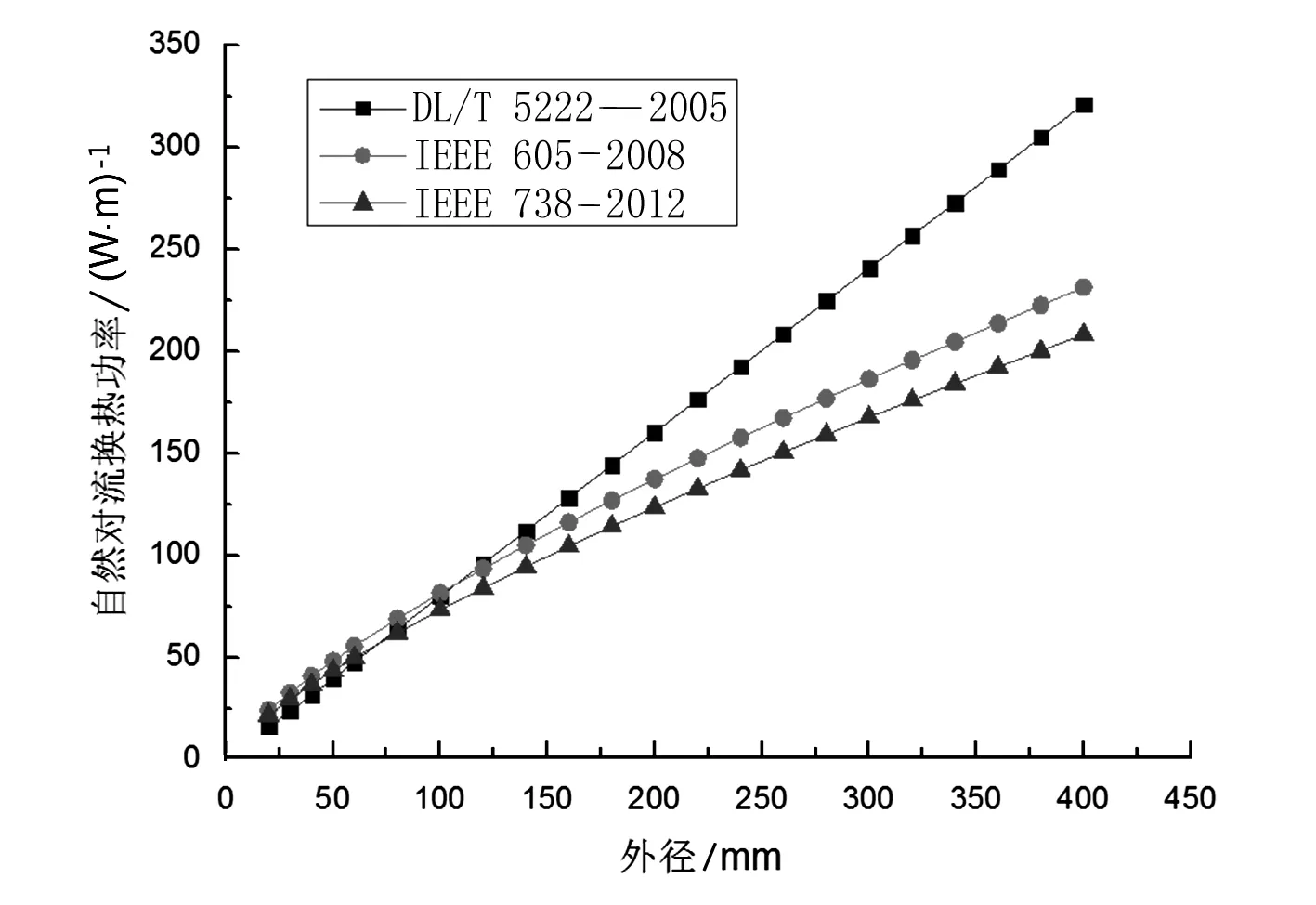
图3 不同计算方法得到的导体自然对流散热功率

3 结 语

上面根据载流量计算的基本原理，给出了换流站中不同载流工况下导体载流量计算的基本原则，确定了适用于换流站导体载流量计算的修正的热平衡方程；在载流量计算方法方面，综合分析比较了电气一次设计手册、DL/T 5222—2005、 IEEE 738—2012、IEEE 605—2008、IEC 61597—1995等5个规程规范给出的交流导体载流量计算方法及其计算结果，重点对比不同的对流散热功率计算方法。分析表明，对于适用于户外导体的强迫对流散热功率，IEEE 738-2012给出的计算方法综合考虑了温度、海拔等因素的影响，比《电气一次设计手册》计算方法更为完备，而根据其原理修正的《电气一次设计手册》计算方法的计算结果则最为保守。考虑IEEE 738—2012不适用于外径大于150 mm的导体，结合国内工程设计实际情况，建议采用修正的《电气一次设计手册》计算方法计算换流站户外导体载流量。对于适用于户内导体的自然对流散热功率，导体外径大于100 mm时采用IEEE 738—2012计算方法更保守；导体外径小于等于100 mm时，采用DL/T 5222—2005计算方法更保守。相关研究结论可供涉外工程设计及换流站导体选择设计相关规程规范的编制参考使用。