线性压缩机圆柱臂盘簧的设计及性能研究
2021-09-13陈洪月张站立吕掌权
陈洪月,张站立,吕掌权
(1.辽宁工程技术大学机械工程学院,辽宁阜新123000;2.中国煤炭工业协会高端综采成套装备动力学测试与大数据分析中心,辽宁阜新123000;3.辽宁工程技术大学矿山液压技术与装备国家地方联合工程研究中心,辽宁阜新123000)
线性压缩机采用直线电机驱动、弹簧组支撑和间隙密封等技术,利用直线电机的运动推动活塞压缩气缸内的气体[1]。它具有结构简单、机械效率高、调控方便等优点,在现代低温斯特林制冷机和脉管制冷机中得到广泛应用[2-6]。弹簧组是线性压缩机的关键部件。它用于支撑活塞,在为活塞的往复直线运动提供足够回复力的同时,使活塞与气缸之间保持合理的密封和运动间隙,避免活塞发生径向偏移,保证活塞往复运动的行程,同时也对延长线性压缩机的寿命起到关键作用[7-9]。
弹簧组中柔性板弹簧的设计种类较多。柔性板弹簧在延长制冷机寿命方面表现出极大的潜力,已逐渐取代柱弹簧[10]。Wong 等[11]对涡旋形弹簧进行了优化设计,提出了涡旋型线的无量纲设计曲线,并将该弹簧应用于早期的牛津型斯特林制冷机。Amoedo 等[12]对柔性板弹簧的设计变量进行了研究,对设计的不同柔性板弹簧的轴向刚度、径向刚度、固有频率和应力进行了比较。Rajesh 等[13]分析了柔性板弹簧的螺旋扫描角、槽宽、螺旋数和厚度等参数对柔性板弹簧性能及疲劳寿命的影响。陈楠[7]提出了圆渐开线设计方法,并结合数学分析模型,对圆渐开线形柔性板弹簧进行动力学分析和应力计算,通过修正后的理论表达式清晰地揭示了板弹簧性能参数与几何参数之间的关系。袁重雨等[14]提出了一种基于费马曲线的柔性弹簧的设计方法,并采用有限元分析方法分析了弹簧结构参数对弹簧性能的影响。
本文设计了一种多线型圆柱臂盘簧。相比柔性板弹簧,它具有加工容易、成本低、刚度大等优点。采用有限元分析方法,分析了盘簧中心线的阿基米德螺线的基圆半径、盘簧线径、盘簧轴向高度等结构参数对盘簧性能的影响。
1 圆柱臂盘簧的设计及应用
线性压缩机圆柱臂盘簧包含2个关于中心空间对称的圆柱弹簧臂。其单臂中心线由4条曲线组合而成,如图1所示。其中:ab为线段,为过渡弧线,为阿基米德螺线,为过渡弧线,为圆弧线。在笛卡尔坐标系下,阿基米德螺线满足:
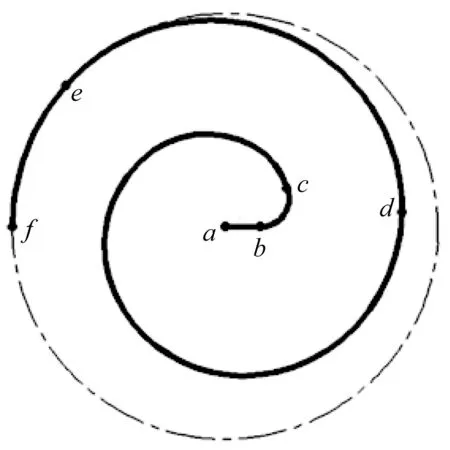
图1 圆柱臂盘簧的单臂中心线Fig.1 Single arm center line of cylindrical arm coil spring
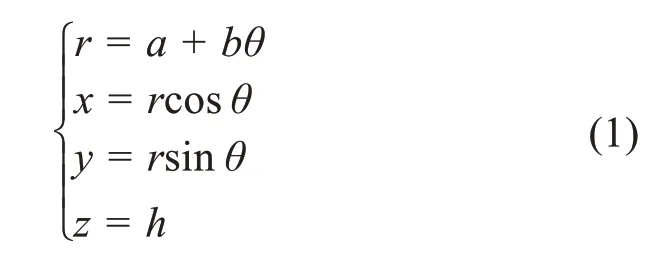
式中:r为螺线极径;θ为极角;a为θ=0°时的基圆半径;b为极角系数;h为阿基米德螺线首尾端点的轴向高度差。
圆柱臂盘簧的轴向高度为a、f两点之间的轴向高度。圆柱臂盘簧模型如图2所示。其中,线径为6 mm,轴向高度为10 mm。

图2 圆柱臂盘簧模型Fig.2 Model of cylindrical arm coil spring
将设计的圆柱臂盘簧应用于线性压缩机。线性压缩机的总装模型如图3所示。其中:盘簧外圈固定在线性压缩机的机架上,盘簧中心通过连接件与活塞轴相连。圆柱臂盘簧与柔性板弹簧的组合作为线性压缩机的弹簧振子系统,为活塞的往复直线运动提供轴向回复力和径向支撑力,保证线性压缩机稳定有效地工作。

图3 线性压缩机总装模型Fig.3 Assembly model of linear compressor
2 圆柱臂盘簧性能的有限元仿真分析
根据线性压缩机结构尺寸的要求,设计的圆柱臂盘簧中心线的外圆弧的直径为134 mm,阿基米德螺线的基圆半径为20 mm,盘簧线径为6 mm,盘簧轴向高度为0 mm。轴向刚度、径向刚度和自振频率是评价柔性弹簧性能的重要指标[15-16]。本文采用ANSYS有限元分析方法对圆柱臂盘簧的性能进行仿真分析。
2.1 圆柱臂盘簧结构的静力学分析
1)建立有限元模型。
通过Pro/E 软件创建圆柱臂盘簧的三维实体模型,将它保存为STP 格式文件导入ANSYS Work‐bench 的Static Structural模块;定义单元类型和材料属性,添加材料为优质硅锰弹簧钢(60Si2MnA),材料的密度为7 908 kg/m3,弹性模量为206 GPa,泊松比为0.3,许用应力为900 MPa;网格尺寸设为2 mm,模型的网格划分如图4所示。
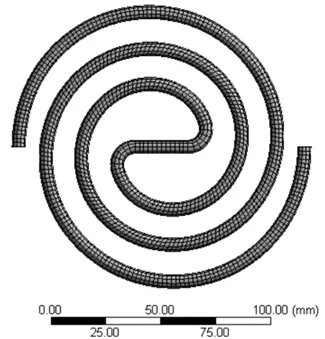
图4 圆柱臂盘簧模型的网格划分Fig.4 Mesh division of cylindrical arm coil spring model
2)设置边界条件。
圆柱臂盘簧的外圆臂固定在线性压缩机的机架上,中心的直线臂通过连接件与活塞轴连接固定。因此,边界条件设置为:外圆臂各节点沿X、Y、Z方向的移动和转动的6个自由度均被约束,对中心直线臂分别施加轴向位移、轴向力和径向力。
3)求解模型。
对圆柱臂盘簧的中心直线臂施加8 mm 的轴向位移,求解得到模型的应力分布如图5所示。由图可知,最大应力出现在盘簧外圆臂固定处附近,为251.92 MPa;在阿基米德螺线臂的内侧出现了应力集中现象,其余部分应力分布较均匀,整体应力远小于材料的许用应力。

图5 施加8 mm 轴向位移时圆柱臂盘簧模型的应力分布Fig.5 Stress distribution of cylindrical arm coil spring model with axial displacement of 8 mm
对圆柱臂盘簧的中心直线臂施加30 N 的轴向力,求解得到模型的位移分布如图6所示。由图可知,最大轴向位移出现在盘簧中心直线臂处,为1.319 mm。
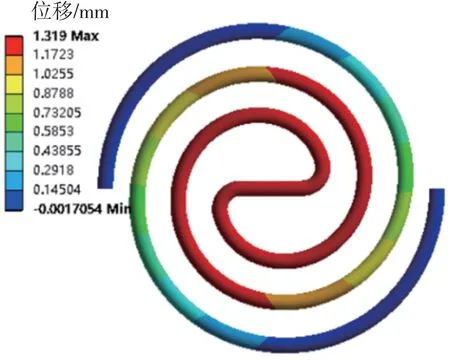
图6 施加30 N轴向力时圆柱臂盘簧模型的位移分布Fig.6 Displacement distribution of cylindrical arm coil spring model with axial force of 30 N
对圆柱臂盘簧的中心直线臂施加20 N 的径向力,求解得到模型的位移分布如图7所示。由图可知,最大径向位移出现在盘簧中心直线臂处,为0.324 4 mm。

图7 施加20 N径向力时圆柱臂盘簧模型的位移分布Fig.7 Displacement distribution of cylindrical arm coil spring model with radial force of 30 N
2.2 圆柱臂盘簧的刚度分析
线性压缩机的活塞作直线往复运动,具有一定的行程。因此,圆柱臂盘簧应具有合适的轴向刚度,以保证活塞在往复直线运动中的可靠性和稳定性;同时,盘簧须有较大的径向刚度,以保证活塞径向的对中性,避免活塞产生侧向力而破坏与气缸之间的配合间隙[17-19]。
根据胡克定律,弹簧的刚度k可以定义为:

式中:F为弹簧受到的轴向力或径向力;X为弹簧产生的轴向位移或径向位移。
通过ANSYS有限元分析和计算,得到圆柱臂盘簧轴向力与轴向位移、径向力与径向位移的关系,分别如图8和图9所示。由图可知,当轴向位移为0.1~8.1 mm,径向位移为0.1~3.1 mm时,轴向力与轴向位移、径向力与径向位移均呈一次函数关系。由式(2)可得设计的圆柱臂盘簧的轴向刚度和径向刚度恒定,分别为22.82 N/mm和62.01 N/mm。
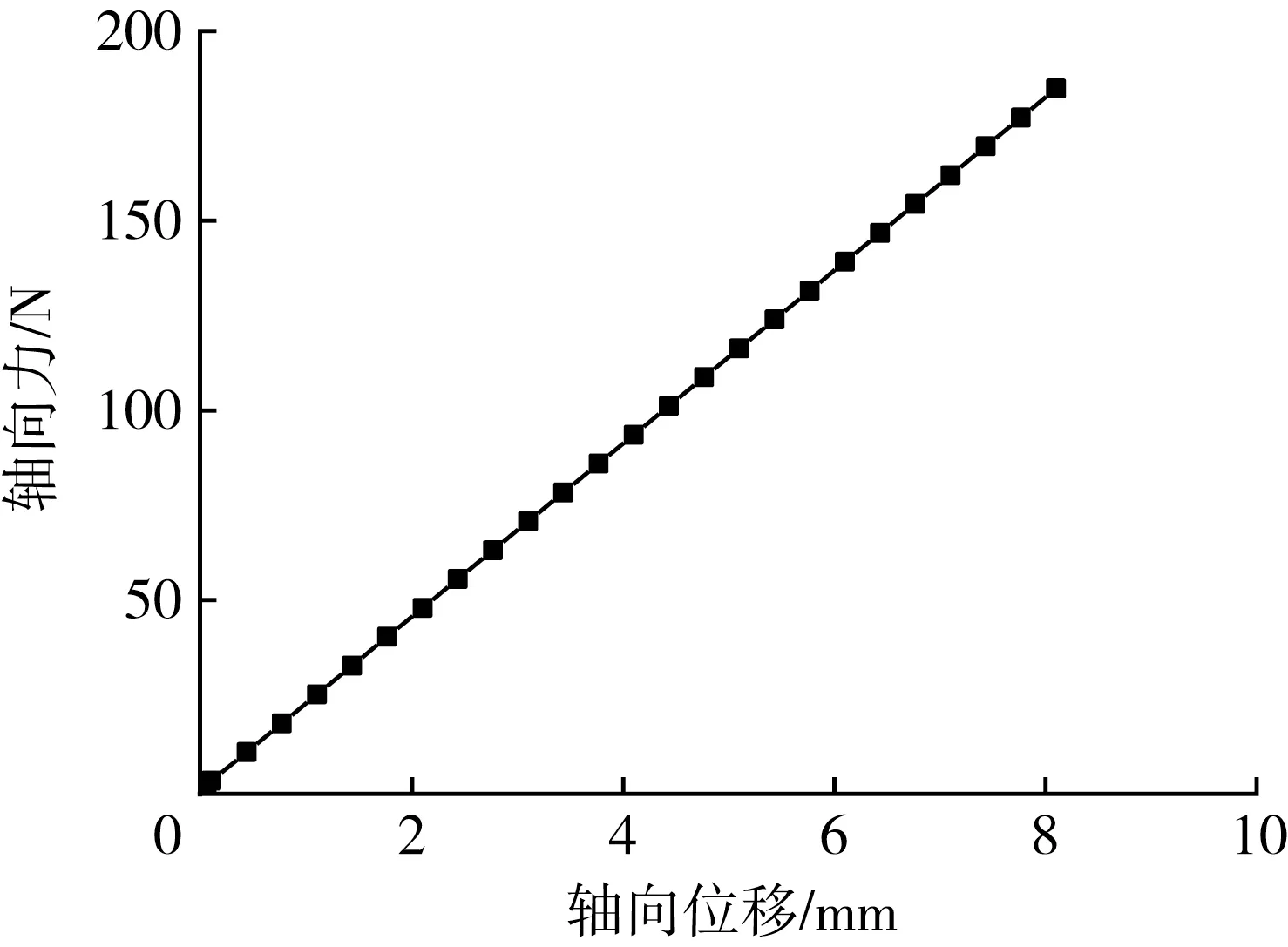
图8 圆柱臂盘簧轴向力与轴向位移的关系Fig.8 Relation between axial force and axial displace‐ment of cylindrical arm coil spring

图9 圆柱臂盘簧径向力与径向位移的关系Fig.9 Relation between radial force and radial displace‐ment of cylindrical arm coil spring
2.3 圆柱臂盘簧的模态分析
通过模态分析可以了解盘簧的振动情况。圆柱臂盘簧的自振频率f满足:

式中:ka为盘簧的轴向刚度;m为盘簧的等效质量。
弹簧的自振频率越大,单位质量的刚度越大,则弹簧的动态性能越好。一般通过叠加多片板弹簧来提高线性压缩机振子系统的共振频率,因此增大了线性压缩机的体积和重量[20]。将具有较高自振频率的弹簧应用于线性压缩机,则在相同的工况下所需的弹簧数量较少[21]。
通过ANSYS有限元分析软件进行模态分析,得到圆柱臂盘簧的前5阶固有频率,如表1所示。其中第1阶固有频率为其自振频率,其模态振型如图10所示。圆柱臂盘簧的自振频率为73.559 Hz。当工作频率与圆柱臂盘簧自振频率一致时,盘簧的形变量较大;第2至第5阶固有频率为盘簧作不规则运动时的频率。可根据盘簧的频率判断盘簧因振动而与其他弹簧发生碰撞的可能性。应根据盘簧的固有频率,合理选择线性压缩机的共振频率,以实现线性压缩机的高效运行。

表1 圆柱臂盘簧的前5阶固有频率Table 1 The first five natural frequencies of cylindrical arm coil spring

图10 圆柱臂盘簧第1阶模态振型Fig.10 The first mode shape of cylindrical arm coil spring
3 圆柱臂盘簧结构参数对盘簧性能的影响
盘簧的结构参数会对盘簧的性能产生较大的影响[22-23]。本文利用ANSYS软件分析圆柱臂盘簧的结构参数对其轴向刚度、径向刚度和应力等性能参数的影响。圆柱臂盘簧的结构参数及对应的性能参数如表2所示。其中,最大应力指对盘簧中心直线臂施加8 mm 轴向位移时圆柱臂盘簧产生的最大应力(下同)。
根据表2第1至第5组数据,可得圆柱臂盘簧性能参数随基圆半径的变化曲线,如图11所示。由图可知:随着基圆半径的增大,圆柱臂盘簧的轴向刚度和最大应力均逐渐减小;径向刚度变化曲线近似为开口向上的二次函数曲线,当基圆半径为19 mm 左右时,径向刚度最小,其主要原因是:基圆半径的变化会使盘簧中心直线臂的长度发生变化,影响弹簧臂排布的紧密程度,并对盘簧的抗拉强度和径向刚度产生复杂的影响。
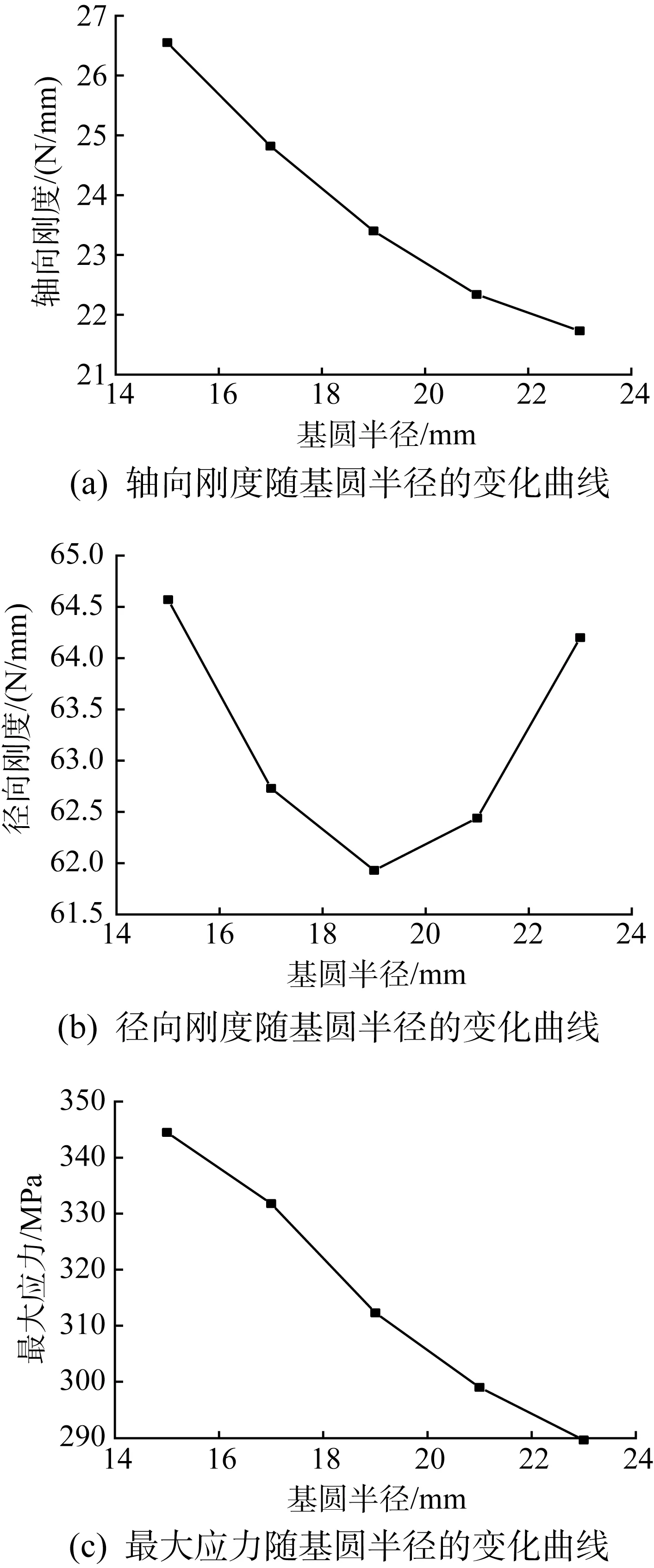
图11 圆柱臂盘簧性能参数随基圆半径的变化曲线Fig.11 Variation curves of performance parameters of cylin‐drical arm coil spring with base circle radius
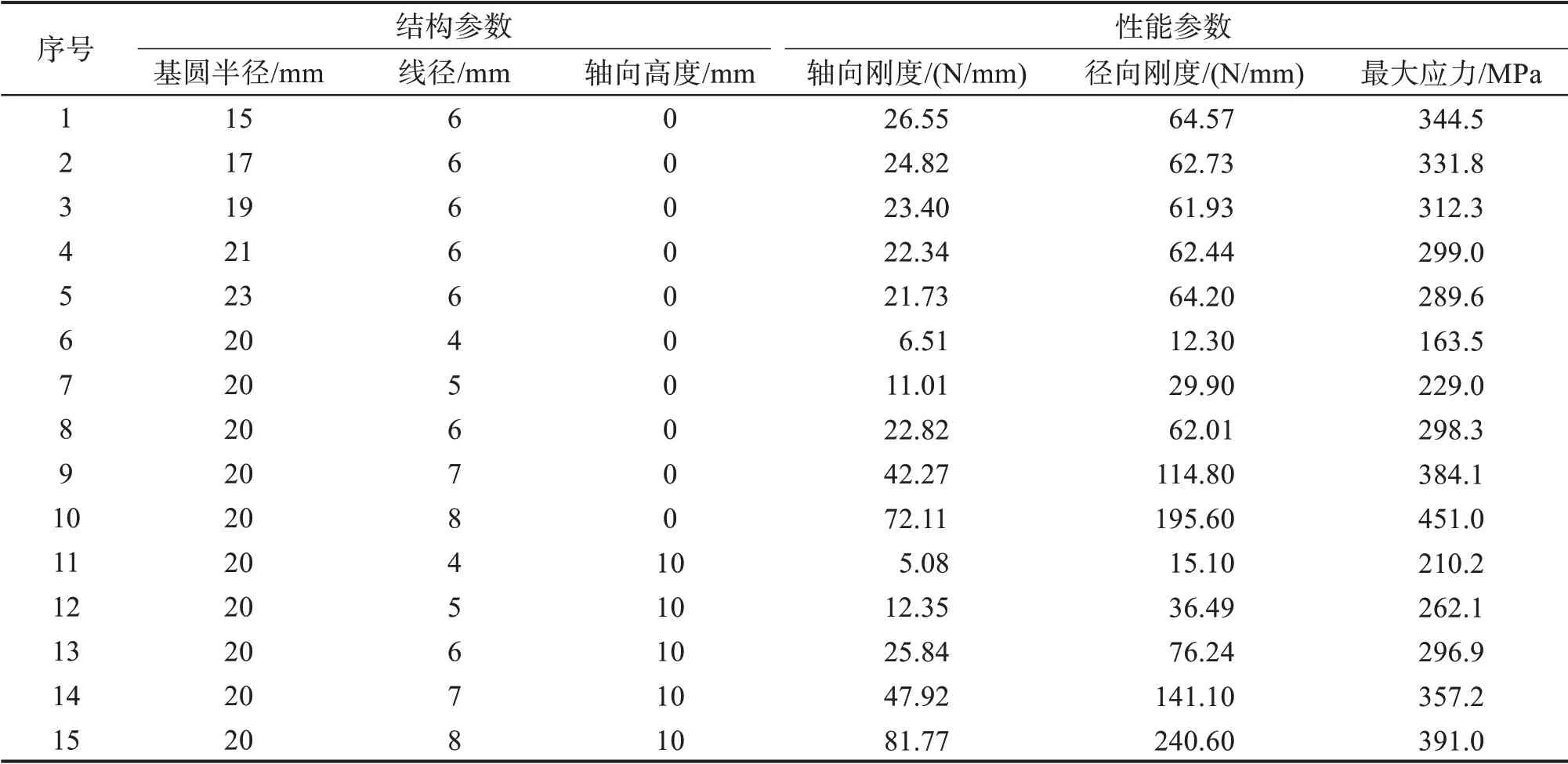
表2 圆柱臂盘簧的结构参数及对应的性能参数Table 2 Structural parameters and corresponding performance parameters of cylindrical arm coil spring
在实际应用中,圆柱臂盘簧须有合适的轴向刚度和较大的径向刚度。当基圆半径为19~23 mm时,轴向刚度较小。因此,在设计圆柱臂盘簧时,应将基圆半径设定在15~19 mm,以使盘簧性能达到最优。
根据表2第6至第15组数据,可得圆柱臂盘簧性能参数随线径的变化曲线,如图12所示。由图可知:随着线径的增大,轴向刚度和径向刚度加速增大;最大应力基本呈线性增大,这是因为随着线径增大,盘簧抗拉强度增大,则最大应力随之增大。
同时,由图12可知:当轴向高度为10 mm 时,盘簧的轴向刚度和径向刚度均略大于轴向高度为0 mm的盘簧,并且随着线径的增大,其差距逐渐增大;盘簧的最大应力均基本随线径的增大呈线性增大;当线径为6 mm时,轴向高度为10 mm的盘簧与轴向高度为0 mm的盘簧产生的最大应力相同,这个交点可以作为盘簧设计的关键参考点,即:当设计的线径小于6 mm 时,优先选择0 mm 的轴向高度;当线径大于6 mm时,优先选择10 mm的轴向高度。
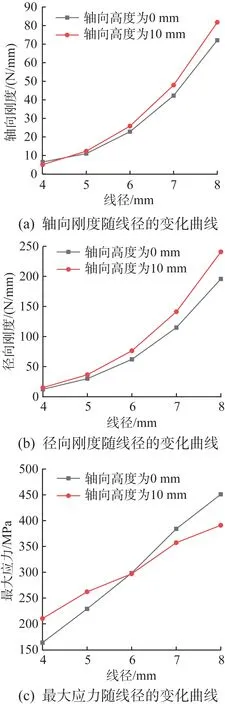
图12 圆柱臂盘簧性能参数随线径的变化曲线Fig.12 Variation curves of performance parameters of cylindrical arm coil spring with line diameter
当线径为4~6 mm时,2种盘簧的刚度差距较小,轴向高度为0 mm的盘簧的最大应力较小;当线径为6~8 mm 时,轴向高度为10 mm 的盘簧的刚度较大,且最大应力较小。因此,在设计圆柱臂盘簧时,若线径为4~6 mm,应优先选择0 mm的轴向高度;若线径为6~8 mm,则优先选择10 mm的轴向高度。
4 结论
笔者设计了一种线性压缩机用多线型圆柱臂盘簧,并采用ANSYS 有限元分析软件,分析盘簧结构参数对其性能的影响。得出以下结论:
1)所设计的圆柱臂盘簧的轴向刚度和径向刚度恒定,可以满足线性压缩机的刚度需求。
2)随着基圆半径的增大,圆柱臂盘簧的轴向刚度和最大应力呈缓慢减小的趋势,径向刚度变化曲线近似为开口向上的二次函数曲线。将基圆半径设定在15~19 mm,有利于提高盘簧的性能。
3)随着线径的增大,圆柱臂盘簧轴向刚度和径向刚度均加速增大,最大应力基本呈线性增大。
4)轴向高度为10 mm的盘簧的轴向刚度和径向刚度均略大于轴向高度为0 mm的盘簧,并且随着线径的增大,其差距逐渐增大。若线径为4~6 mm,应优先选择0 mm 的轴向高度;若线径为6~8 mm,则优先选择10 mm的轴向高度。
