一种可重构的空间开/闭链6R移动并联机构的设计与分析

2021-09-13张春燕蒋新星朱锦翊卢晨晖

工程设计学报 2021年4期

陈致，张春燕，蒋新星，朱锦翊，卢晨晖

（上海工程技术大学机械与汽车工程学院，上海201620）

近年来，并联机构作为机器人领域的重要分支，已广泛应用于工业、农业和医疗等领域［1-4］。并联机构具有独特的闭环特性，常被用作移动机器人的移动机构［5］，可大大提高机器人的刚度和承载能力。例如：陈昊等［6］研制了一款以并联机构为腿部机构的步行机器人，其足端具有6个自由度，可在复杂地面环境下工作；何研颖等［7］以平面六杆机构为本体，设计了一种两轮移动机器人，其结构紧凑，质量较小，具有高机动性，可实现轮式移动；Kong［8］设计了一种六杆单环机构，其利用分岔点的切换来实现在地面上的循环平移。

相较于传统的移动并联机构，可重构移动并联机构不仅具有承载能力强、刚度大和动态特性好等优点，还具有可重构特性。面对多种工作环境，可重构移动并联机构可通过改变自身的构型来完成不同的任务，其受到了学者们的广泛关注［9-12］。例如：Liu 等［13］利用平面四杆机构与六杆机构，设计了一种可重构移动并联机构，其具有滚动和步行两种模式；刘超等［14］结合地面移动需求，利用机构分岔点来实现模式切换，设计了一种具有类蠕动、平面4R（转动副）转向和内翻模式的地面移动机构；姚舜等［15-16］将2 个经典的Schatz 机构组合设计成一种可实现单动力转向爬行的移动机器人，分析了其移动机理并通过试验样机验证了其转向控制方法的可行性。上述研究表明，可重构移动并联机构可通过构型切换来适应不同的地形。

为提高移动并联机构的地形适应能力，以平面开/闭链6R机构为基本单元，设计了一种可重构的空间开/闭链6R移动并联机构。基于单环6R机构的打开与闭合，所设计的机构可实现折叠、足式越障和滚动等多种运动模式的相互转换。首先，基于螺旋理论对所设计的机构在不同运动模式下的自由度进行分析；然后，建立所设计机构的运动学模型，对其足式越障性能和滚动模式的可行性进行分析；最后，利用ADAMS（auto‐matic dynamic analysis of mechanical systems，机械系统动力学自动分析）软件对所设计机构的运动模式进行仿真分析和验证。

1 新型可重构移动并联机构的结构设计与运动模式分析

1.1 结构设计

图1所示为可重构的空间开/闭链6R移动并联机构的三维模型，其由4条相同的支链和上、下平台组成。其中，呈对称分布的每条支链均由2个转动副和1个万向副（U）组成，与上平台连接的万向副可等效为轴线相交的2个转动副。按顺时针方向对支链编号，分别为支链1，2，3，4。由支链1，3（2，4）与上、下平台形成的2个平面开/闭链6R机构在空间上正交；上、下平台均为“十”字形板，其中上平台为固定的“十”字上板，下平台由4块下板组成。

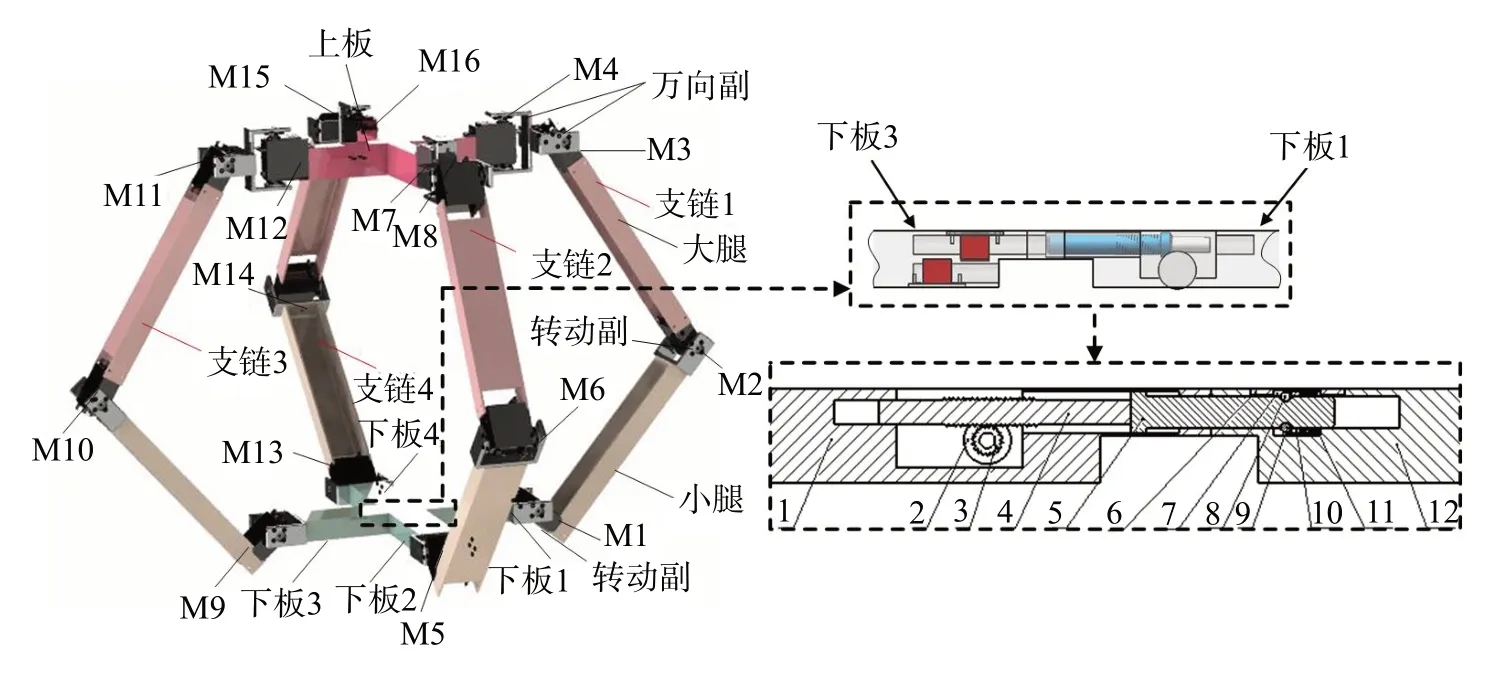
图1 可重构的空间开/闭链6R移动并联机构的三维模型Fig.1 Three dimensional model of reconfigurable spatial open/closed chain 6R mobile parallel mechanism

对于由2 条对称的URR 支链和上、下平台组成的平面开/闭链6R 机构，基于下平台的结构特点，该机构可实现打开与闭合。在该平面开/闭链6R 机构中，开合电机固定在下板3的卡槽内；由自锁壳体、压紧滚珠1、压紧滚珠2、压环和弹簧组成的自锁装置安装在下板1的卡槽内。在平面开/闭链6R机构由打开到闭合的过程中，先启动驱动电机M9，使得下板3与上平台平行，然后启动驱动电机M1，使得下板1与下板3的接口对准，最后开合电机通电，带动蜗轮转动，进而带动蜗杆运动，在蜗杆的推动下自锁推杆进入自锁装置，从而使开链闭合。同理，当闭链打开时，开合电机断电后自锁推杆向后移动，依次启动驱动电机M1 和M9，使得下板1，3 依次打开后折叠进入小腿内，从而使闭链变成开链。

图2所示为可重构的空间开/闭链6R移动并联机构的结构简图。以支链1为例，其小腿与下平台的连接点为转动副A1、腿与大腿的连接点为转动副B1，大腿与上平台的连接点为万向副。其中，转动副A1、B1与万向副等效的第一转动副C1的轴线平行，与万向副等效的第二转动副D1的轴线垂直。整个可重构移动并联机构共有16 个驱动电机，支链1 中A1、B1、C1和D1处分别装有驱动电机M1、M2、M3和M4。

图2 可重构的空间开/闭链6R 移动并联机构的结构简图Fig.2 Structure diagram of reconfigurable spatial open/closed chain 6R mobile parallel mechanism

1.2 运动模式分析

由于平面开/闭链6R机构既具有闭链6R机构的多边形几何变形特性［17］，又具有开链6R机构的支链末端散点着陆功能。因此，基于开/闭链6R机构的打开与闭合，可实现所设计可重构移动并联机构的多种运动模式，如表1所示。在初始位型下，可重构的空间开/闭链6R 移动并联机构是一个结构对称的并联机构，由于其单条支链中的2个转动副与万向副等效的第一转动副相互平行，则整个机构可等效成具有虚约束的Sarrus机构［18］，其可实现沿上、下平台方向的折叠，即折叠模式。依次启动相应的驱动电机，使2个闭链6R机构打开，该移动并联机构可从初始位型切换到双向四足越障模式；继续驱动万向副等效的第二转动副，使2 个正交的开链6R 机构重构为平行状态，则可切换为单向四足越障模式。在单向四足越障模式下，依次启动相应的驱动电机，使2个开链6R机构关闭，则该移动并联机构可切换到滚动模式，此时万向副等效的2个转动副的轴线相互垂直，通过转动第二转动副来使2 个平行的闭链6R 机构正交，可切换回折叠模式。

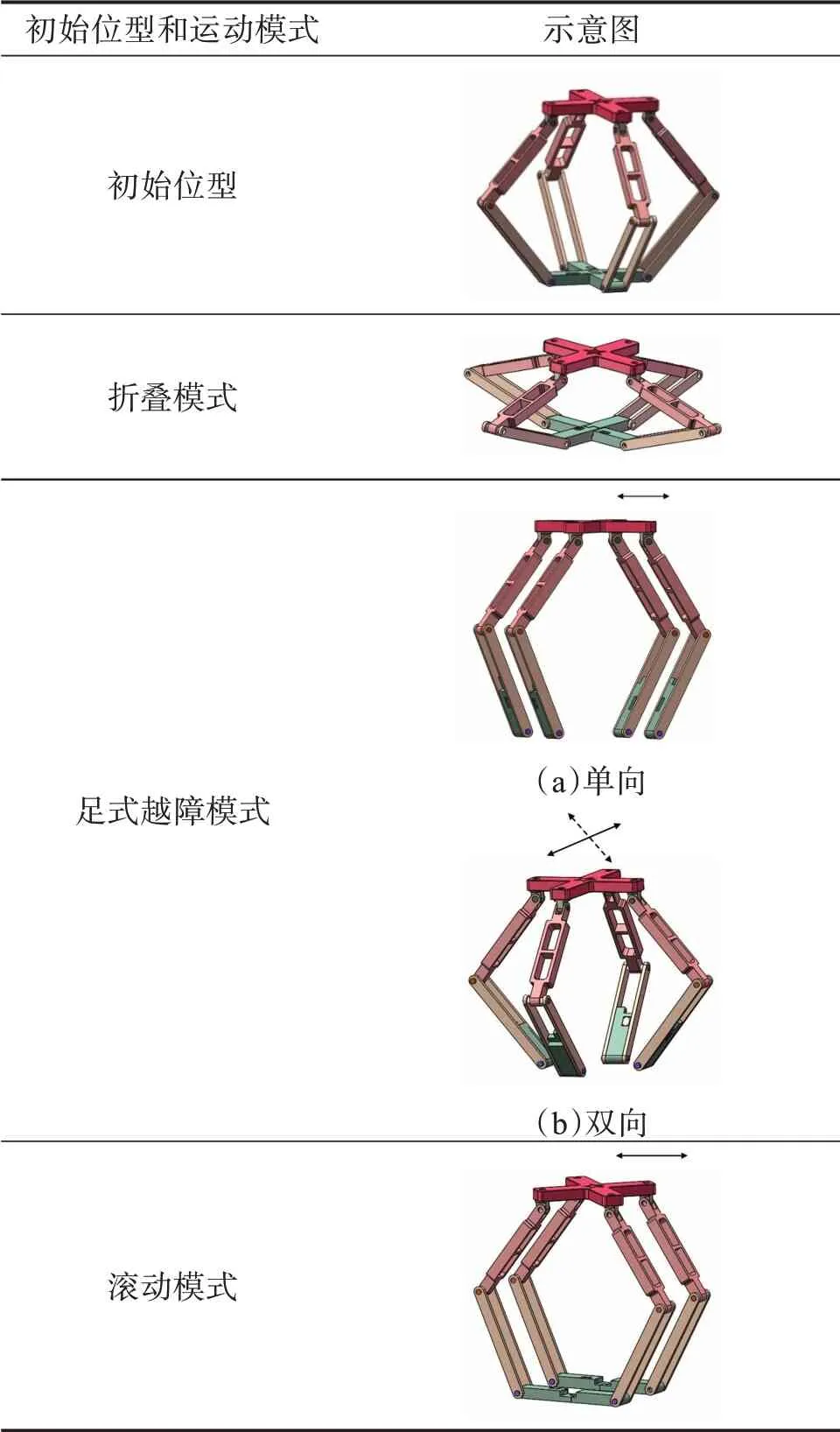
表1 可重构的空间开/闭链6R移动并联机构的初始位型和运动模式Table 1 Initial configuration and motion modes of recon‐figurable spatial open/closed chain 6R mobile par‐allel mechanism

要实现可重构的空间开/闭链6R 移动并联机构的各个运动模式，须使该机构在各运动模式下具有不同的自由度。基于螺旋理论，对各运动模式下机构的自由度及运动性质进行分析。先建立不同运动模式下机构的坐标系，其中坐标系原点均位于转动副A1的中心处，转动副A1的轴线方向为x方向，竖直向上方向为z方向。不同运动模式下可重构的空间开/闭链6R移动并联机构的运动螺旋及自由度如表2所示（鉴于机构的结构对称，只给出单条支链的螺旋示意）。表中：a12、a13、a14、b12和b13分别为各转动副有向螺旋线段的方向数；d12、d13、e12和e13分别为有向螺旋线段相对原点的距离沿x、y方向的分量。

表2 不同运动模式下可重构的空间开/闭链6R移动并联机构的运动螺旋及自由度Table 2 Kinematic helix and degree of freedom of reconfigurable spatial open/closed chain 6R mobile parallel mechanism under different motion modes

由表2可知，对于可重构的空间开/闭链6R移动并联机构，当处于折叠模式时，其每条支链有2个约束螺旋，机构过约束，其上平台只有1个沿z方向的移动自由度；当处于足式越障模式时，机构处于开链状态，不存在约束，其共有6个自由度，即沿x、y、z方向的平移自由度和绕x、y、z方向的转动自由度；当处于滚动模式时，其每条支链有3个约束螺旋，则整个机构有3个公共约束，可等效为三自由度（沿y、z方向的平移自由度和绕x方向的转动自由度）的平面6R连杆机构。

2 新型可重构移动并联机构的运动性能分析

对复杂地形的适应能力是可重构移动并联机构的重要性能指标之一。对复杂地形的适应能力主要包括跨越障碍的能力、跨越沟渠的能力以及爬坡能力等。为适应移动过程中的地形变化，应保证可重构的空间开/闭链6R移动并联机构在足式越障、滚动等运动模式下的性能。

2.1 足式越障模式分析

2.1.1 D-H坐标系构建

在足式越障模式下，可重构的空间开/闭链6R移动并联机构的4块下板收至小腿内，其可等效为连杆机构。构建该机构单支链的D-H 坐标系，分别以转动副D1、C1、B1（将转动副视作关节）为原点建立坐标系：o1-x1y1z1、o2-x2y2z2、o3-x3y3z3，其中o1-x1y1z1是基坐标系，如图3所示。该支链的D-H 参数如表3 所示。其中：θi为关节转动角度（θ1为万向副等效的第二转动副的轴线与竖直方向的夹角；θ2为大腿与万向副等效的第一转动副的轴线之间的夹角；θ3为大腿与小腿之间的夹角）；di为相邻关节的y向距离；li为连杆长度（l1为万向副长度；l2为大腿长度；l3为小腿长度）；αi为相邻关节轴线之间的角度。

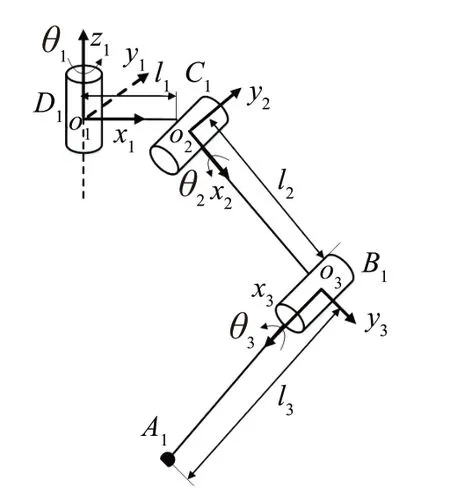
图3 足式越障模式下可重构的空间开/闭链6R 移动并联机构单支链的D-H坐标系Fig.3 D-H coordinate system of single branch chain of recon‐figurable spatial open/closed chain 6R mobile parallel mechanism under foot-type obstacle crossing mode

表3 足式越障模式下可重构的空间开/闭链6R移动并联机构单支链的D-H参数Table 3 D-H parameters of single branch chain of reconfigu‐rable spatial open/closed chain 6R mobile parallel mechanism under foot-type obstacle crossing mode

2.1.2 足式越障模式运动学分析

根据表3 的D-H 参数和相邻2 个坐标系间的变换矩阵，得到足式越障模式下可重构的空间开/闭链6R移动并联机构单支链的正运动学方程及其足端的期望位姿。其中，相邻2个坐标系间的变换矩阵为：

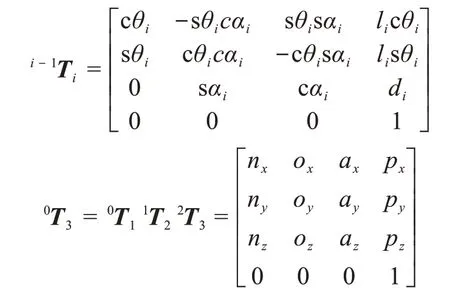
式中：c=cos，s=sin；上标0表示以上平台中心为原点构建的坐标系o0-x0y0z0。

由此可得，足式越障模式下该机构支链足端的位置为：

当万向副长度为20 mm、大腿长度为250 mm、小腿长度为250 mm时，利用MATLAB软件绘制可重构的空间开/闭链6R 移动并联机构支链足端的工作空间，如图4所示。其中：图4（a）、（b）分别为支链足端工作空间（即足端可达位置的集合）在x1o1y1、y1o1z1平面上的投影。从图4中可以看出，该机构在足式越障模式下的最大跨度（x1方向）约为450 mm，最大步长（y1方向）约为400 mm，最大抬腿高度（z1方向）约为480 mm。

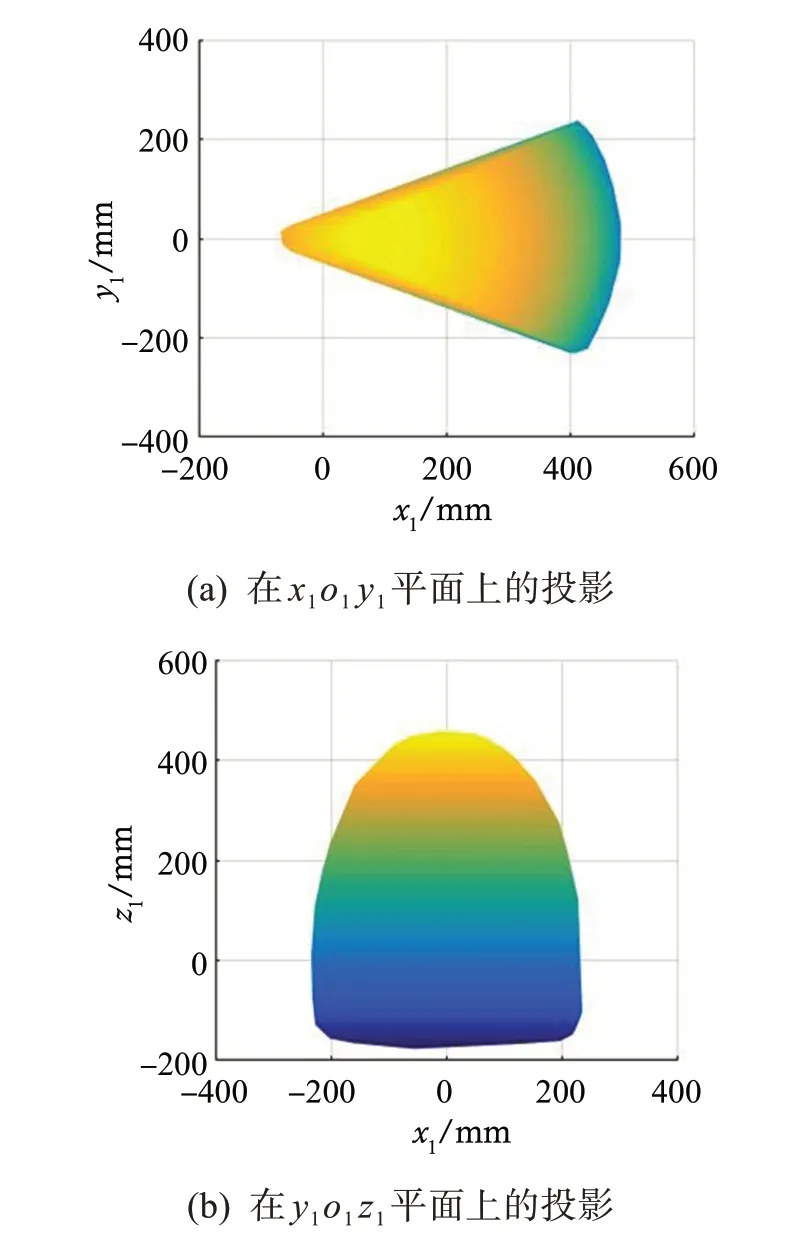
图4 可重构的空间开/闭链6R 移动并联机构支链足端的工作空间Fig.4 Workspace of branch chain end of reconfigurable spa‐tial open/closed chain 6R mobile parallel mechanism

2.1.3 足端越障分析

在越障过程中，可重构的空间开/闭链6R移动并联机构的运动主要包括每条支链的俯仰运动和摆动运动，以越过一定宽度和高度的障碍物。

如图5所示，可重构的空间开/闭链6R移动并联机构的某支链在平面内由A点（起始点）摆动到B点（落点）。设万向副至A点的距离为L1，L1在摆动平面内的投影长度为L3；万向副至摆动平面的竖直距离为L2；万向副至B点的距离在摆动平面内的投影长度为L4；万向副在摆动平面内投影点至B点的距离沿y、x方向的分量为L5、L6。

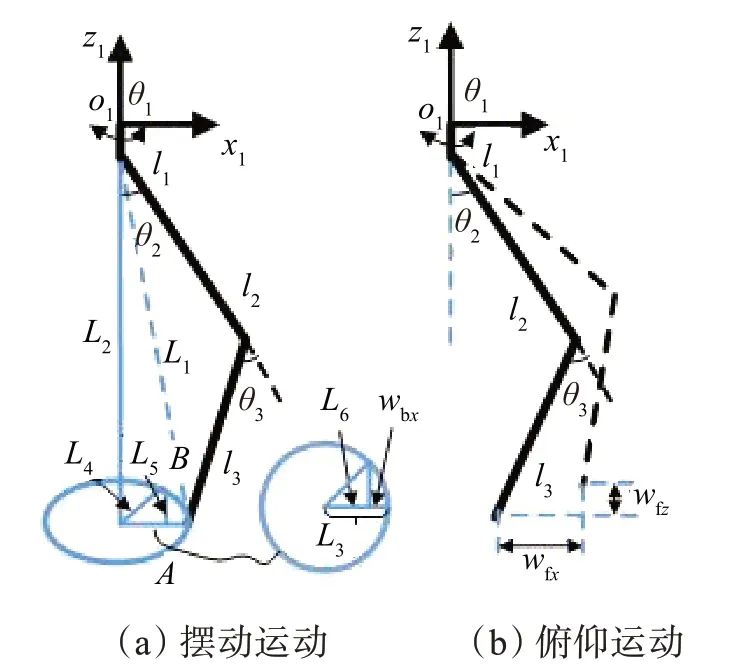
图5 可重构的空间开/闭链6R 移动并联机构单支链的运动简图Fig.5 Kinematic diagram of single branch chain of re‐configurable spatial open/closed chain 6R mo‐bile parallel mechanism

由图5可得：

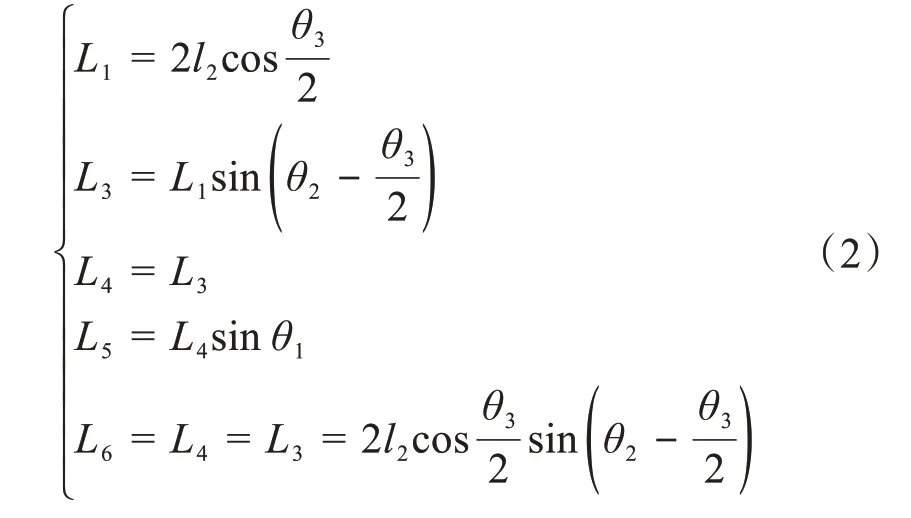
当支链作摆动运动时，其足端的x向位移wbx为：

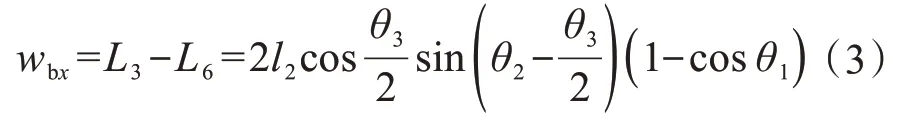
当支链作俯仰运动时，其足端的x向位移wfx为：

由图5 可知，支链作摆动运动时，其z向位移不变，仅在作俯仰运动时产生z向位移。在支链作俯仰运动的过程中，其足端的z向位移wfz为：

如图6所示，当可重构的空间开/闭链6R移动并联机构处于单向足式越障模式时，其一次所能越过的障碍宽度wx和障碍高度wz分别为俯仰运动时产生的x向和z向位移，即：

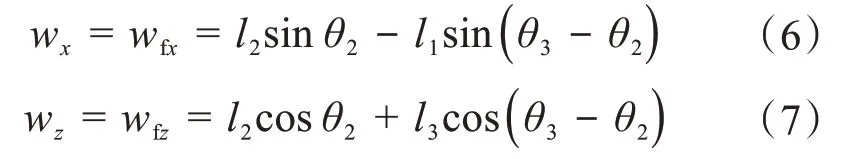
图6 可重构的空间开/闭链6R 移动并联机构单向越障运动学分析Fig.6 Kinematic analysis of one-way obstacle crossing of reconfigurable spatial open/closed chain 6R mobile parallel mechanism

如图7所示，当可重构的空间开/闭链6R移动并联机构处于双向越障模式时，其一次所能越过的障碍宽度wx为摆动运动产生的x向位移wbx与俯仰运动产生的x向位移wfx之和，越过的障碍高度wz为俯仰运动产生的z向位移wfz，即：

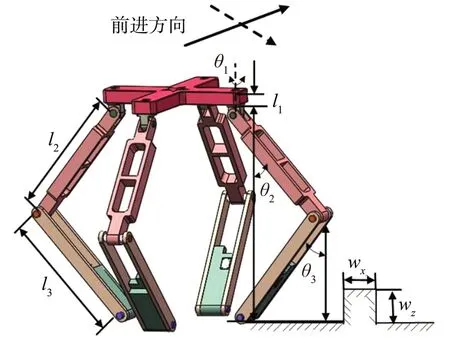
图7 可重构的空间开/闭链6R 移动并联机构双向越障运动学分析Fig.7 Kinematic analysis of bidirectional obstacle crossing of reconfigurable spatial open/closed chain 6R mobile parallel mechanism

在足式越障模式下，可重构的空间开/闭链6R移动并联机构一次所能越过的障碍宽度wx和与θ2、θ3之间的关系如图8所示，一次所能越过的障碍高度wz与θ2、θ3之间的关系如图9所示。

由图8 可知，两曲面相交处表示单向和双向足式越障模式下可重构的空间开/闭链6R 移动并联机构一次所能越过的障碍宽度相同；在交线左侧，表示单向足式越障模式下机构所能越过的障碍宽度较大；在交线右侧，表示双向足式越障模式下机构所能越过的障碍宽度较大。由图9 可知，无论是单向还是双向足式越障模式，该机构一次所能越过的障碍高度相同，均为0～180 mm。

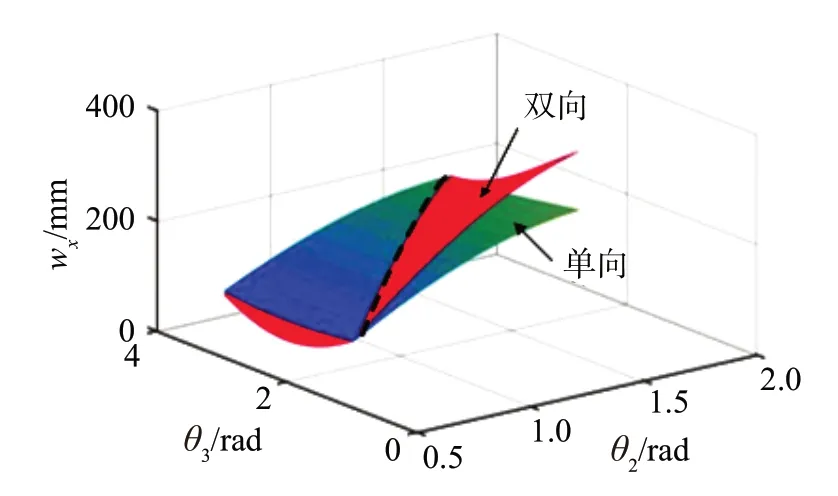
图8 越障宽度wx与θ2、θ3的关系Fig.8 Relationship between obstacle crossing width wx and θ2，θ3

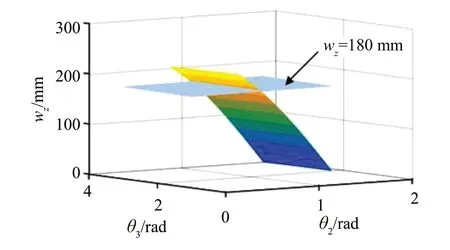
图9 越障高度wz与θ2、θ3的关系Fig.9 Relationship between obstacle crossing height wz and θ2，θ3

2.2 滚动模式分析

2.2.1 运动学分析

由上文分析可知，当可重构的空间开/闭链6R移动并联机构处于滚动模式时，整个机构可等效为平面6R连杆机构。如图10所示，以转动副A1中心为原点构建直角坐标系o-xyz，其中x方向为转动副A1的轴线方向，z方向为竖直向上方向。图中：γ1、γ2、γ3为驱动杆5，3，1 与相邻杆6，4，2 之间的角度；ϕ1、ϕ2、ϕ3为非驱动杆4，2，6与相邻杆5，3，1之间的角度；各杆长度均为a；η1、η2、η3为△A1B2C1的内角；Gj（j=1，2，…，6）为各杆件的质心。

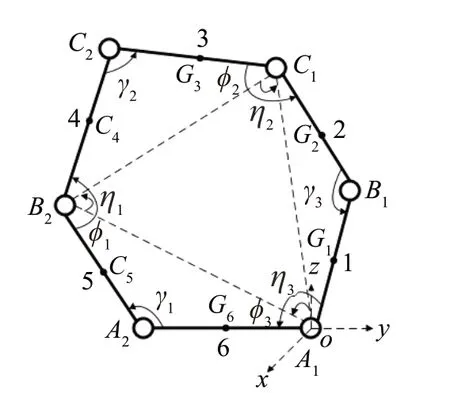
图10 可重构的空间开/闭链6R移动并联机构滚动模式简图Fig.10 Rolling mode diagram of reconfigurable spatial open/closed chain 6R mobile parallel mechanism

由图10可知，滚动模式下可重构的空间开/闭链6R移动并联机构共有3个自由度，可任意选择3个转动副作为驱动副。为使构型对称，此处选转动副A2、C2、B1作为驱动副。根据图10可得，△A1B2C1的边长为：

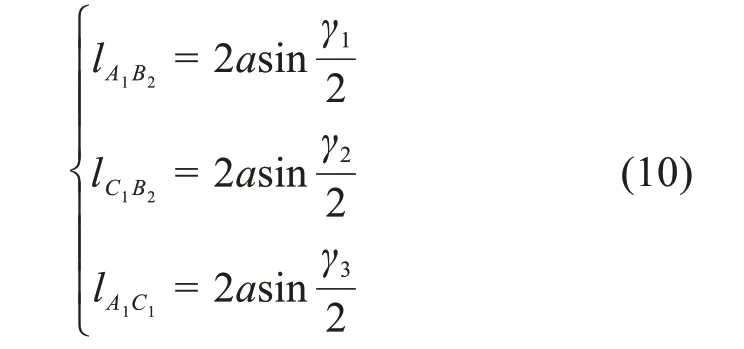
△A1B2C1的内角为：

根据图10的几何关系，求得非驱动杆与相邻杆间的角度：

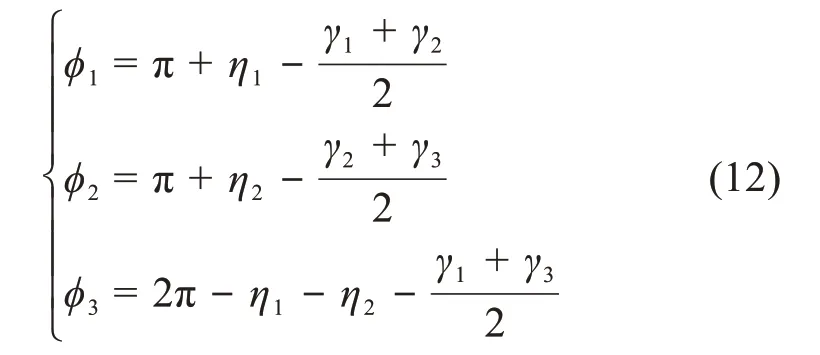
2.2.2 可行性分析

质心是用于判断机构运动稳定性的重要指标。当可重构的空间开/闭链6R 移动并联机构处于滚动模式时，须持续调整姿态。考虑各杆件的质量，机构的质心坐标可表示为：

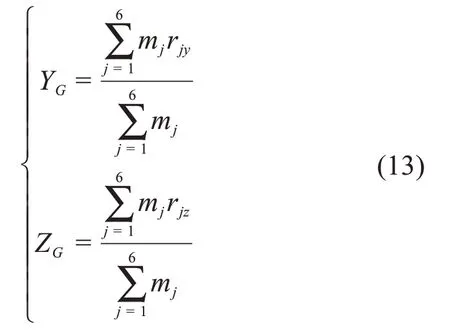
式中：mj为第j个杆件的质量；rjy、rjz为杆件j的几何中心的y、z坐标。

当驱动角度发生变化时，可重构的空间开/闭链6R移动并联机构的质心会发生变化。如图10所示，忽略连杆的厚度，假设机构中所有杆件的质量相同且均匀分布，均为m；各杆件的质心位于其几何中心处。非驱动杆6 与地面接触，其几何中心OG的坐标为将机构各杆件的质心坐标代入式（13），得到机构质心坐标与输入角γ1、γ2的关系。图11和图12所示分别为机构质心的z坐标与输入角γ1、γ2的关系及对应的等高线；图13和图14所示分别为机构质心的y坐标与输入角γ1、γ2的关系及对应的等高线。由图11 和图12 可知，机构质心的z坐标始终大于0 mm，满足滚动运动的条件。因此本文主要对机构质心的y坐标进行分析。

图11 机构质心的z坐标ZG与输入角γ1、γ2的关系Fig.11 Relationship between z coordinate ZG of mechanism mass center and input angle γ1，γ2

图12 机构质心的z 坐标ZG 与输入角γ1、γ2 关系的等高线示意图Fig.12 Contours diagram of relationship between z coordinate ZG of mechanism mass center and input angle γ1，γ2

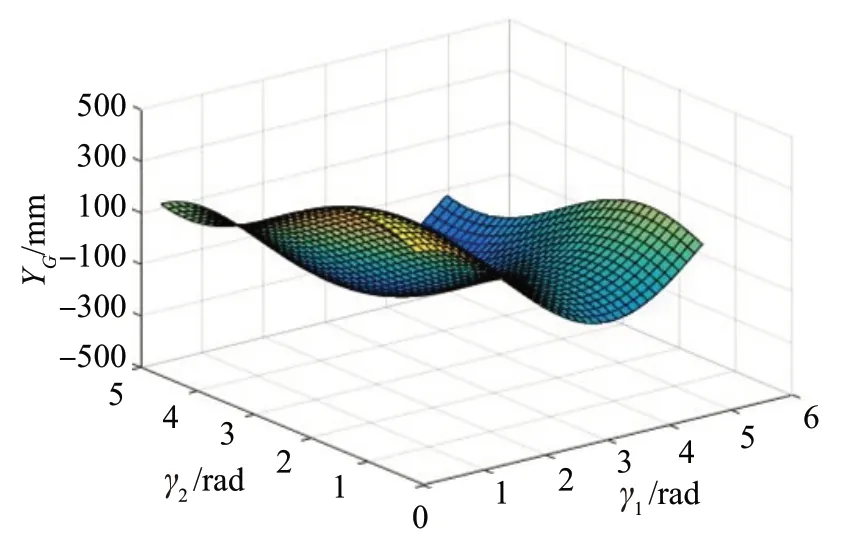
图13 机构质心的y坐标YG与输入角γ1、γ2的关系Fig.13 Relationship between y coordinate YG of mecha‐nism mass center and input angle γ1，γ2

图14 机构质心的y 坐标YG 与输入角γ1、γ2 关系的等高线示意图Fig.14 Contours diagram of relationship between y coordinate YG of mechanism mass center and input angle γ1，γ2

由图13和图14可知，当机构质心的y坐标小于0 mm时，不满足机构滚动时的稳定性条件，即机构处于失稳状态；当机构质心的y坐标大于0 mm时，满足机构滚动时的稳定性条件，即机构处于稳定状态。综上可知，当0 rad<γ1<2 rad、0 rad<γ2<3.5 rad时，YG>0mm，即机构处于稳定状态；当2 rad<γ1<5 rad、3.5 rad<γ2<5 rad时，YG<0 mm，即机构处于失稳状态。

3 仿真试验验证

利用ADAMS 软件对可重构的空间开/闭链6R移动并联机构的运动模式进行仿真分析，以验证各运动模式的可行性。设l2=l3=250 mm，并给定θ1、θ2和θ3的值。

3.1 折叠模式仿真分析

设置驱动电机为M2，其速度ω=π rad/s，对折叠模式下的可重构的空间开/闭链6R移动并联机构进行仿真分析，得到其上平台的位移变化曲线，如图15所示。由图可知，该机构初始位置为状态a，驱动1 s后，机构到达状态b，机构展开至杆件BkCk(k=1，2，…，4)与杆件Bk Ak(k=1，2，…，4)趋向平行；驱动至t=1.7 s时机构到达状态c，至此完成了1个周期的折叠。

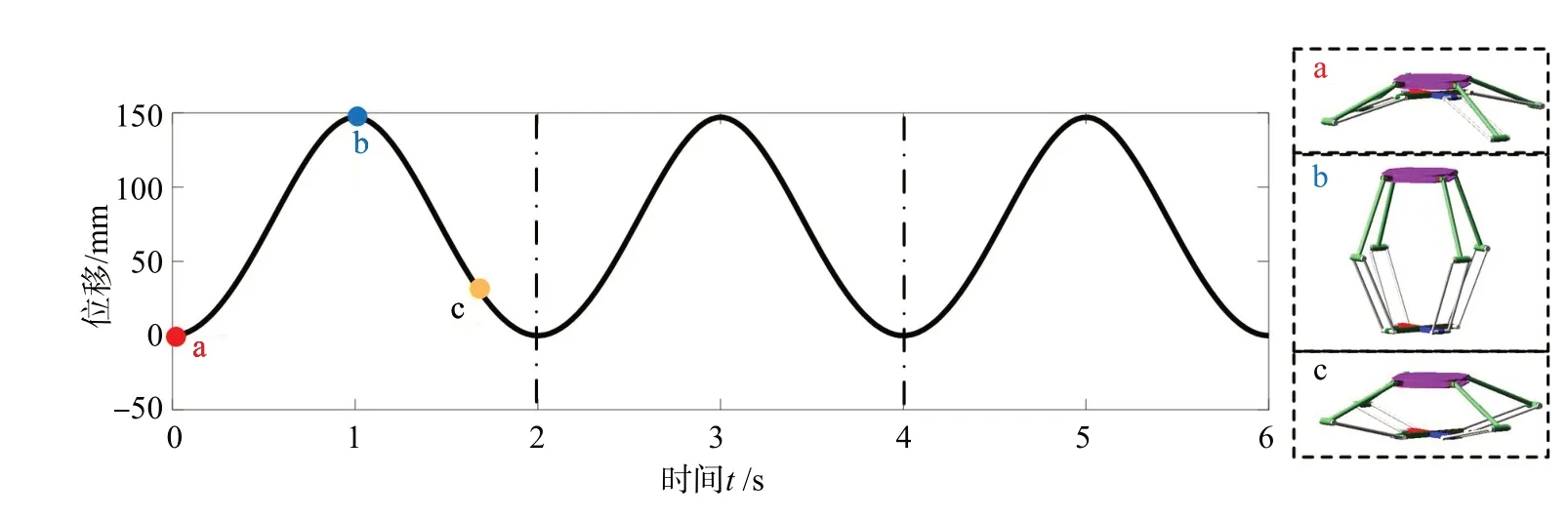
图15 可重构的空间开/闭链6R移动并联机构折叠模式仿真分析结果Fig.15 Simulation analysis results of folding mode of reconfigurable spatial open/closed chain 6R mobile parallel mechanism

3.2 足式越障模式仿真分析

联合除M1、M5、M9和M13外的驱动电机，对足式越障模式下的可重构的空间开/闭链6R 移动并联机构进行仿真分析，得到其上平台的位移变化曲线，如图16所示。由图可知，当机构在状态a时为足式越障模式的初始状态；运动0.5 s后，机构到达状态b，此时，机构向前迈步；运动0.8 s后，机构继续运动至状态c，至此完成了1个周期的足式越障运动。

图16 可重构的空间开/闭链6R移动并联机构足式越障模式仿真分析结果Fig.16 Simulation analysis results of foot-type obstacle crossing mode of reconfigurable spatial open/closed chain 6R mobile par‐allel mechanism

3.3 滚动模式仿真分析

联合驱动电机M1、M3和M14，得到滚动模式下可重构的空间开/闭链6R 移动并联机构上平台的位移变化曲线，如图17所示。当机构处于状态a时，为滚动模式的初始状态；运动0.5 s时，机构到达状态b，此时机构处于运动状态，杆件AkBk(k=1，2，…，4)与杆件CkBk(k=1，2，…，4)的角度发生变化，机构质心向y轴正向移动；机构继续运动至杆件AkBk(k=1，2，…，4)着地，即到达状态c；运动至5 s时，上平台运动至接地位置；运动至10 s时，机构到达状态f，至此完成了1个周期的滚动。

图17 可重构的空间开/闭链6R移动并联机构滚动模式仿真分析结果Fig.17 Simulation analysis results of rolling mode of reconfigurable spatial open/closed chain 6R mobile parallel mechanism