变基圆半径涡旋膨胀机型线参数的优化选取
2020-09-29王永强
彭 斌,蒋 龙,王永强
(兰州理工大学机电工程学院,甘肃兰州730050)
自1984年Morishita首次建立圆渐开线涡旋型线的分析模型后,各国学者开始对涡旋机械进行深入研究。如:Matsuba等人对涡旋压缩机的发展进行了总结和展望[1];Lindsay等人研究了制造功能性涡旋压缩机时圆渐开线涡旋型线所需具备的几何特性[2];Chen等人建立了涡旋压缩机的工作模型,并对其工作时的受力、热传递和泄漏情况进行了分析[3];王向红对涡旋膨胀机的泄漏损失进行了数值计算和分析[4];Wang等人对涡旋压缩机涡旋型线的数学模型进行了推导[5]。
虽然圆渐开线涡旋型线的数学模型较为成熟,且由其展成的涡旋机械较容易加工,但该涡旋型线展成时的可变参数较少,很难通过改变参数来提升涡旋机械的性能,因此学者们开始寻求可提升涡旋机械性能的新型线。Qing等人提出了一种膨胀腔腔体不对称的涡旋压缩机,并对其性能进行了研究[6];Hwang等人提出了以椭圆为基准所展成的涡旋型线[7];王吉岱等人对采用变基圆半径渐开线型线的涡旋膨胀机进行了研究,并推导了其工作腔容积的计算公式[8];Wang等人研究了多种渐开线的性能特点,提出了涡旋型线啮合的计算方法[9];Shaffer等人建立了多种由齿头修正后的几何模型,并基于预设的几何参数对修正后涡旋型线展成的膨胀机的吸气腔容积进行了计算[10]。
变基圆半径涡旋型线是指其基圆半径随着展开角增大而连续变化的渐开线,由其展成的涡旋齿壁厚会随着展角逐渐变大或变小,从而实现性能的改变。同时,由于它与圆渐开线涡旋型线极其相似,由其展成的涡旋机械的加工难度较低。丁佳男等人对变基圆半径涡旋型线的方程进行了详细推导,并对该型线的端部进行了双圆弧修正[11];唐景春等人对比了在气体温度和压力耦合的工况下圆渐开线涡旋型线和变基圆半径涡旋型线的应力、应变,并对后者进行了齿头修正[12-13]。
随着学科的交叉发展,智能算法开始广泛应用于涡旋型线的优化。陈进等人利用多目标遗传算法对组合型线进行了优化分析,得到了具有较高效率、较高体积利用率的组合型线,但该类组合型线的中间段为非渐开线,导致加工难度较大,而且在对多个参数同时优化时容易出现解为负值的情况,既降低了算法的准确率又增加了迭代次数[14];王立存等人采用小生境遗传算法对通用涡旋型线进行优化研究后发现,由于通用型线可变参数的局限性,其性能提升效果并不明显[15];刘涛等人利用MATLAB遗传算法工具箱提供的多目标遗传算法对三段基圆渐开线涡旋型线进行了优化,然而,由于遗传算法工具箱的输入形式固定,必须将所有公式合并后才能进行输入和计算,这增加了优化前的工作量[16]。
在运算时,粒子群算法的运算效率高于遗传算法,且变基圆半径涡旋型线较组合型线有较好的连续性,更容易加工,所以本文采用粒子群算法对变基圆半径涡旋型线的参数进行优化分析,为变基圆半径涡旋膨胀机的型线设计提供参考。
1 变基圆半径涡旋型线的数学模型
1.1 变基圆半径涡旋型线的公转半径和膨胀起始角
变基圆半径涡旋型线静盘型线求解为[17]:

式中:a为初始基圆半径;k为基圆变化系数;φ为渐开线展成角;α为渐开线发生角。
由式(1)可知:当k<0时,基圆半径随渐开线的不断展开而变小,壁厚也随之减小;当k=0时,基圆半径保持不变,壁厚不发生变化;当k>0时,基圆半径随渐开线的不断展开而变大,壁厚也随之增大。图1所示为不同k对应的变基圆半径涡旋型线。

图1 不同k对应的变基圆半径涡旋型线Fig.1 Variable base circle radius vortex profiles corresponding to different k
变基圆半径涡旋型线的公转半径和膨胀起始角分别为:
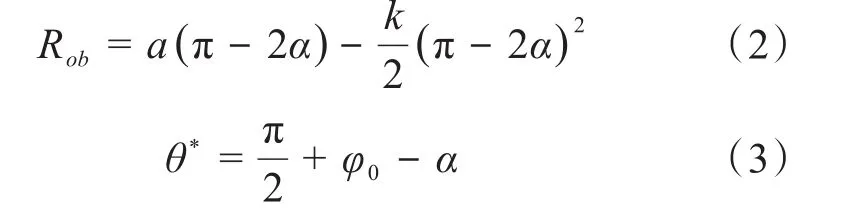
式中:φ0为涡旋型线啮合点处内侧型线的展角,可根据φ0+2φ0sin(φ0-α)+2cos(φ0-α)=(π-α)2-2求解。
1.2 动静涡旋盘的啮合盘径
动静涡旋盘是涡旋膨胀机的核心部件,其啮合盘径的大小直接影响涡旋膨胀机整体结构的设计,进而决定了涡旋膨胀机的质量大小。动静涡旋盘啮合盘径作为涡旋膨胀机的关键结构参数,在不影响其性能的前提下越小越好。
变基圆半径涡旋型线动静涡旋盘的啮合盘径为:
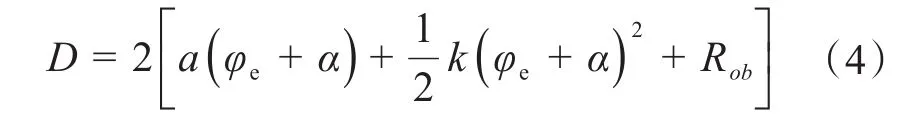
式中:φe为渐开线最终展开角。
1.3 变基圆半径涡旋膨胀机的膨胀比
涡旋膨胀机的膨胀比是最后一个膨胀腔的容积与吸气腔容积的比值,用来表征涡旋膨胀机的膨胀性能。在一定尺寸下,膨胀比越大,涡旋膨胀机的性能越好。可通过增大渐开线最终展开角(即增加涡旋型线的展开圈数)或改变涡旋型线类型来增大膨胀比,但最终展开角的增大会使动静涡旋盘的啮合盘径增大,从而导致膨胀机的体积和质量增大。
膨胀比的计算公式如下:

式中:V为变基圆半径涡旋膨胀机最后一个膨胀腔的容积;V吸为变基圆半径涡旋膨胀机吸气腔的容积。
第i个膨胀腔的容积求解如下:

式中:h为涡旋齿齿高;A为变基圆半径涡旋膨胀机的腔体面积[18]。
2 基圆变化系数对变基圆半径涡旋膨胀机性能优化的影响
2.1 优化目标和优化参数的确定
由式(4)和式(5)可以看出,与啮合盘径D和膨胀比σ取值有关的参数为初始基圆半径a、渐开线最终展开角φe、渐开线发生角α、基圆变化系数k和公转半径Rob,其中:Rob可由a、α、k三个参数求解得到;α是与渐开线开始展开时的起始位置有关的参数,与D和σ皆成正比,鉴于其影响有限,在优化时选取α=2π/9;φe是控制涡旋型线最终展成位置的参数,即控制涡旋型线的展开圈数以及工作腔个数,该参数对除排气腔外的其余工作腔无影响,且对膨胀比的影响较小,故在优化时选定φe=20.41。
综上,选取涡旋膨胀机的基本尺寸参数D和基本性能参数σ为优化目标,以初始基圆半径a和基圆变化系数k为优化参数,对变基圆半径涡旋膨胀机的涡旋型线进行优化,以寻求优化参数在一定范围内变化时,单个优化目标的最优解和2个优化目标的非劣解集。
由公式(1)可以看出,当基圆变化系数k不变,仅考虑初始基圆半径a的影响时,其对变基圆半径涡旋型线的影响与对传统圆渐开线的影响相同,故下面只针对基圆变化系数k的影响进行分析。
2.2 基圆变化系数k对啮合盘径D的影响
选取a=3.2mm,α=2π/9,φe=20.41,根据式(4)得到基圆变化系数k与啮合盘径D的关系曲线,如图2所示。

图2 基圆变化系数k与啮合盘径D的关系曲线Fig.2 Relationship curve between base circle variation coefficient k and mesh disc diameter D
根据图2可知,在其他参数一定的情况下,啮合盘径D随着基圆变化系数k的增大而增大,且两者呈线性正比关系,故基圆变化系数k的选取对啮合盘径D有重要影响。
2.3 基圆变化系数k对各膨胀腔容积Vi的影响
选取a=3.2mm,α=2π/9,φe=20.41,根据式(6)和式(7)得到基圆变化系数k与各膨胀腔容积Vi的关系曲线,如图3所示。
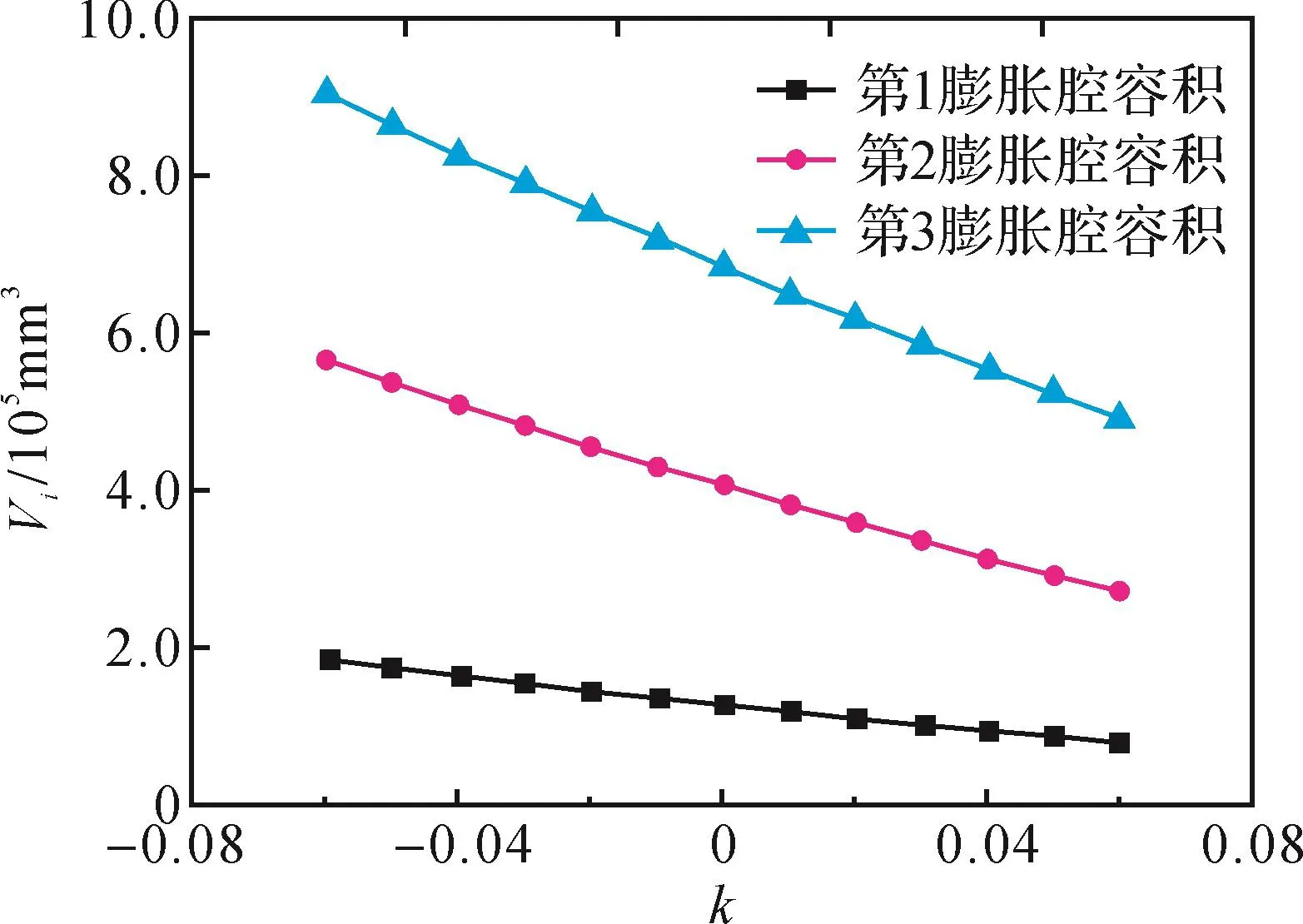
图3 基圆变化系数k与各膨胀腔容积Vi的关系曲线Fig.3 Relationship curve between base circle variation coefficient k and volume of each expansion cavity Vi
由图3可知:在啮合盘径D一定、相同的基圆变化系数k下,涡旋膨胀机各腔容积由内向外依次变大,这是涡旋膨胀机能够实现膨胀功能的原因;k越小,各膨胀腔的容积越大。这就说明,在相同啮合盘径D下,选取较小的基圆变化系数k可以增加有效容积,从而优化膨胀机的性能。
3 基于粒子群算法的变基圆半径涡旋型线参数的优化
3.1 粒子群算法
粒子群算法是一种群体智能优化算法,算法中的每个粒子都代表一个潜在解,每个粒子均有3个属性参数,分别为位置、适应度值和速度。其中:粒子的位置表示该粒子此时的取值与群体最优解的距离;粒子的适应度值表示优化目标的解;粒子的速度决定了粒子的移动方向和大小,用于实现位置的更新。粒子群算法的流程如图4所示。图中,实线箭头指引的流程为单目标粒子群优化算法流程,而多目标粒子群优化算法流程要附加虚线所指引的非劣解判断流程,这是多目标优化与单目标优化的主要区别。
3.2 单目标多参数优化
分别以啮合盘径D和膨胀比σ为优化目标,以初始基圆半径a和基圆变化系数k为共同优化参数进行优化,结果如图5所示。其中:选取Rob=5.6155mm,α=2π/9,φe=20.41。
由图5可知,基于粒子群算法的单目标优化效率非常高,仅通过2或3次迭代就可以完成寻优。在以a和k为共同优化参数对单个目标进行优化时,啮合盘径D取得最小值93.374 5 mm时,膨胀比σ=4.306 0;膨胀比σ取得最大值6.253 9时,啮合盘径D=182.435 1 mm。由此可知,啮合盘径D和膨胀比σ可分别取得各自的最优值,但对应的σ和D并非最优。故对单个目标进行优化时,只能实现局部目标的最优。
3.3 多目标单参数优化
以1/D和σ为共同优化目标,分别以a和k为优化参数进行优化,结果如图6所示。其中:图6(a),选取Rob=5.6155mm,α=2π/9,φe=20.41,a=3.2mm;图6(b),选取Rob=5.6155mm,α=2π/9,φe=20.41,k=-0.02。选择对1/D而不是对D进行优化的原因在于:在多目标粒子群优化过程中,粒子只能向着同一种变化趋势进行运动,即粒子的速度只能是朝着正向或者负向进行更新,当选择D为优化目标时,粒子需要朝负向运动,而当选择σ为优化目标时,粒子需要朝正向运动,为保证粒子的运动方向一致,选用作为优化目标。
在图6中,黑点代表该次优化结束时所有粒子的适应度值,空心圆代表所有粒子在经过非劣解选择后所保留的非劣解。
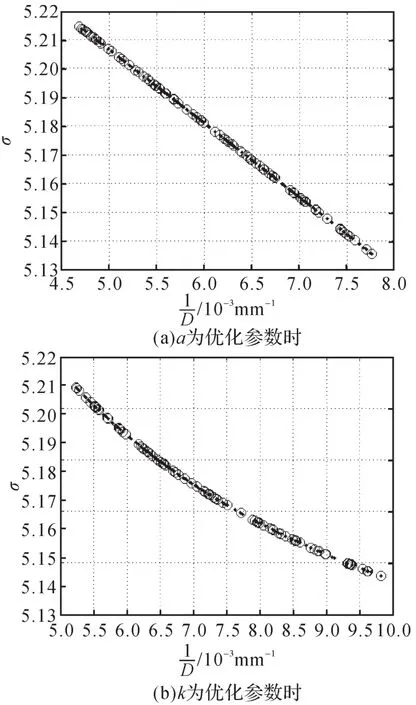
图6 参数a和k单独优化时多目标和σ的优化结果Fig.6 Optimization results of multi-objective and σ with parameter a and k optimized separately
为了更直观地分析,分别从各优化目标的非劣解集中挑选3组非劣解进行分析,结果如表1所示。由图6和表1可以看出,在其他条件不变的情况下,膨胀比σ增大时,啮合盘径D均会有所增大,即无法实现在膨胀比取得极大值的同时啮合盘径取得极小值。因此,在对变基圆半径涡旋膨胀机进行型线设计时,可根据性能或尺寸优化的要求,来选择相应的参数。
3.4 多目标多参数优化
以1/D和σ为共同优化目标,以a和k为共同优化参数进行优化,结果如图7所示。其中:选取Rob=5.6155mm,α=2π/9,φe=20.41。为了更直观地分析,从优化目标的非劣解集中挑选2组非劣解进行分析,结果如表2所示。
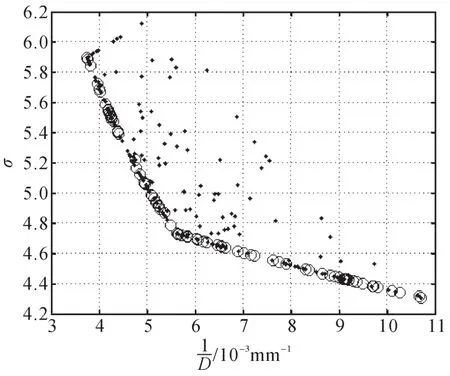
图7 参数a和k同时优化时多目标和σ的优化结果Fig.7 Optimization result of multi-objective and σ with parameter a and k optimized simultaneously

表2 参数a和k同时优化时D和σ的非劣解Table 2 Non-inferior solutions of D and σ with parameter a and k optimized simultaneously
对比图7和图5可以看出,当以a和k为共同优化参数时,单目标优化时可得到一个最优解,而多目标优化时能得到一组非劣解。因此,可根据设计要求的侧重点不同,选择相对满足要求的一组优化参数组合。
对比图7与图6可以看出,当以1/D和σ为共同优化目标时,单参数优化所得的优化目标取值范围较小。这说明多优化目标、多优化参数的粒子群优化算法可以更加全面地对变基圆半径涡旋型线进行优化。
4 结 论
当分别以D和σ为单独优化目标时,可在a和k的取值范围内分别得到D和σ的极值;若该极值不满足设计要求时,可以参照a和k对D和σ的影响来调整其取值范围,这可为初始参数的选取提供参考。
当以D和σ为共同优化目标时,可在a和k的取值范围内得到一组非劣解,此时D和σ值是兼顾结构和性能要求的一组较均衡的解。
综上,当对变基圆半径涡旋膨胀机进行整体设计时,可根据其结构和性能的要求,选取满足条件的初始基圆半径a和控制基圆变化系数k。
