高中数学主题教学设计应把握四个关键点

王祥芬

摘  要：高中数学主题教学设计，目的是在教学中培养学生的数学学科核心素养，帮助学生整体把握数学、抓住本质、学会学习，落实立德树人根本任务. 文章以“函数单调性”为例，论述高中数学主题教学设计应把握四个关键点，即从教学内容的确定上要把握学习知识、思想方法、学科素养的整体性;从学习目标的定位上要把握课程、主题、课时的结构性;从教学过程的实施上要把握由浅入深、由易到难的层次性;从教学评价的方式上要把握激励、动态的发展性.

关键词：数学学科核心素养;主题教学设计;数学本质;函数的单调性

高中数学教学要以发展学生的数学学科核心素养为导向，引导学生把握数学本质，凸显数学的内在逻辑和思想. 因此，有必要精选和优化课程内容进行主题教学设计，从单一的课时设计到章节设计，再到主题教学设计. 数学主题教学设计是在整体思维指导下，从提升学生数学核心素养的角度出发，对相关教材内容进行统筹重组和优化，并将优化后的教学内容视为一个相对独立的教学主题，以突出数学内容的主线及知识间的关联，在此基础上对教学内容进行改进的动态教学设计. 为了帮助教师准确理解和整体把握知识体系，提升教师主题教学设计的站位，笔者以函数单调性在教学中的应用为例，论述高中数学主题教学设计应把握的四个关键点.

一、把握主题教学内容的关键点——整体性

主题教学设计是指以教材为基础，对教材中具有某种关联性的内容进行分析、重组、整合、提炼，有目标、有计划、有评价地组织的整体性教学，它具有知识整体性、问题关联性、方法聚焦性等特点. 可以将两章或两章以上的内容整合，围绕同一个主题组织教学，每个章节相互配合，最终达到甚至超越原课程设置的目标.

主题教学内容的确定要依据《普通高中数学课程标准（2017年版）》（以下简称《标准》）、教材、学情来整体设计，可以是重要的数学概念或核心数学知识，也可以是重要的数学思想方法（如数形结合、转化与化归、函数与方程思想等），还可以是以数学学科核心素养、基本能力为主题. 每个类型的主题都要形成知识网络图，将《标准》、教材、学情、基本思想、基本活动经验、数学学科核心素养等进行整体分析. 例如，函数单调性是函数的重要性质之一，是高中数学学习的重要内容，在高中各个年级分别有不同的内容和应用. 高一学习时与函数概念、函数的其他性质、基本初等函数有关，高二学习时与数列、导数等内容有关，在高中阶段表述过程中还与常用逻辑用语中的量词有关. 因此，函数单调性可以作为跨章节的主题进行整体教学设计. 高中数学课程中有很多这样主题鲜明、内容综合的知识需要跨章节设计，在为学生搭建学习核心内容的框架的同时，也为学生自主选择学习的切入点建立整体联系，实现教学设计与素养目标的有效对接.

主题教学内容分析要站在知识系统的高度，依据《标准》，从基础性、发展性、可行性等角度整体分析，分析本主题内容的数学本质、数学文化、数学思想及数学基本活动经验;分析本主题内容在本学段数学课程中的地位;分析本主题内容在整个中小学数学课程中的地位和作用;分析本主题内容在数学整体中的地位;分析与本学段、前后学段及大学其他知识之间的联系.

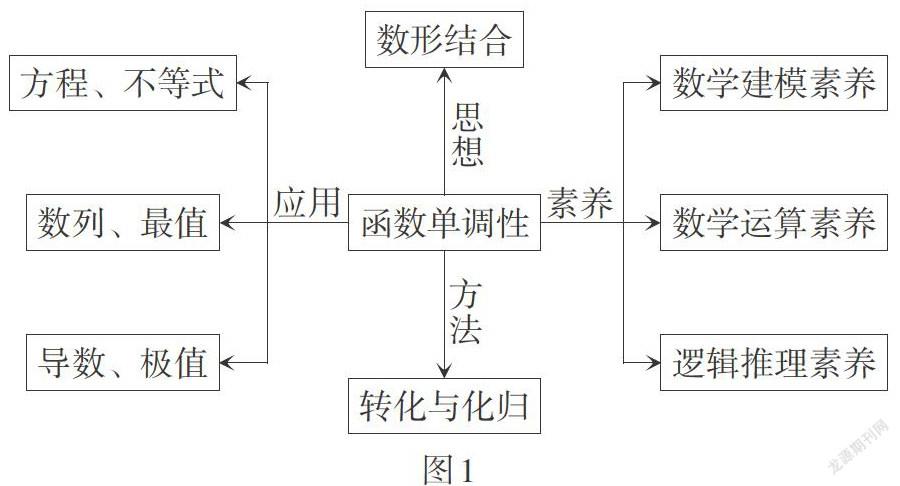
“函数单调性”主题教学内容的网络图如图1所示.

由图1可知函数单调性和不等式是相互交融的两部分内容，利用不等式研究函数单调性是知识基础，利用函数单调性研究不等式更是妙趣横生. 函数单调性与最值密不可分，用函数单调性研究最值问题和值域问题是函数应用中最有效、最严谨的方法. 由于數列[an]中的[an]可以看成是关于自变量[n n∈N∗]的函数，故可以通过函数单调性来解决有关数列的最值问题.

利用导数可以一般性地研究函数单调性，感悟导数是研究函数单调性强有力的工具，深刻理解函数单调性的本质.

二、把握主题学习目标的关键点——结构性

主题教学中的目标设计具有明显的结构性特点，它由课程目标、主题目标、课时目标组成. 把握主题学习目标要考虑四个因素：一是《标准》的要求;二是学习主题与核心内容;三是数学学科核心素养的进阶发展;四是学生的学习基础和发展需求. 由此可见，主题学习目标的结构性很强，既要体现数学学科核心素养，又要指向对学科本质的理解，还要指向学生的未来发展，目标之间相互关联、相互支撑. 设计主题学习目标时，通常可以分为三个步骤：第一步依据《标准》结合学习内容深入分析，明确学生应该学习的内容和达到的水平标准，设计主题学习核心目标;第二步明确主题学习的每个课时的目标，指向基础关键的问题;第三步研讨、修订和完善，最终确定主题学习目标. 绘制目标结构图是呈现主题学习目标的常用方法.

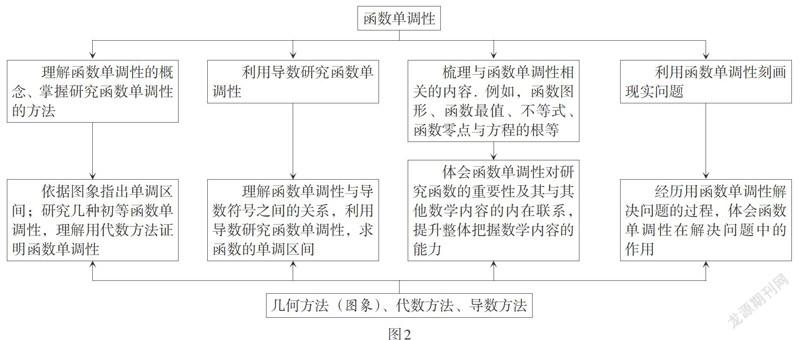
函数单调性课程目标为：理解单调性的作用和实际意义. 主题目标为：经历用几何方法、代数方法和导数方法研究函数单调性的过程，理解函数单调性的概念、掌握研究函数单调性的方法;通过梳理与函数单调性相关的内容，提升整体把握函数单调性的能力;经历用函数单调性解决问题的过程，体会函数单调性在解决问题中的作用，提升数学抽象、直观想象、逻辑推理、数学运算、数学建模等数学学科核心素养.

函数单调性学习目标结构图如图2所示.

三、把握主题教学过程的关键点——层次性

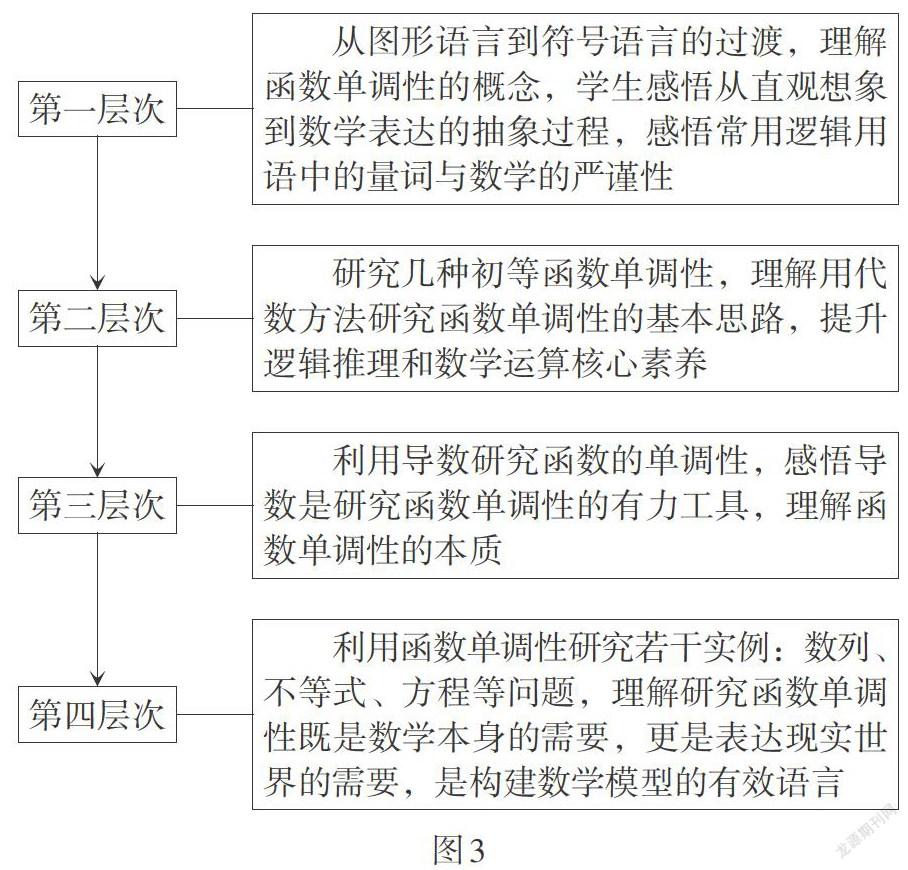
主题教学内容涉及若干节，甚至涉及若干章，因此在设计教学过程时，可以划分为不同的层次. 主题内每节课之间依据知识的系统性，按照由浅入深、由易到难的顺序设计，形成教学的坡度和训练的梯度，使教学有目的、有计划地进行. 主题内各节课之间既相对独立，有各自承担的教学任务和分工，又彼此联系，前一节课的内容为后一节课的节点和生长点，教学活动逐层递进，呈阶梯式、螺旋式前进. 因此，教学过程的设计，要分析出由学习起点到学习终点必须经历的关键节点，学生关于这些节点具有的学习基础和应有的学习基础，以及学生在学习新知识时可能遇到的障碍，然后依序操作、层层落实，最终通过各节课的教学完成主题教学任务.

以函数单调性知识的前后逻辑为线索，设置如图3所示的四个教学层次.

四、把握主题教学评价的关键点——发展性

教学评价是数学教学活动的重要组成部分，主题教学活动的评价，要以教学目标的达成为依据，关注学生对数学知识的掌握情况，更要关注学生数学学科核心素养的发展水平，以及学生在学习活动中的参与度、积极性及创新能力. 评价是为了激励，利用学习分析、课堂观察等大数据技术，采用多元评价方式，让每名学生都有展示的机会. 持续而发展的教学评价是主题教学中不可缺少的环节. 同时，教师可以基于对学生的评价，反思自己的教学过程，总结经验、发现问题，提出教学改进思路.

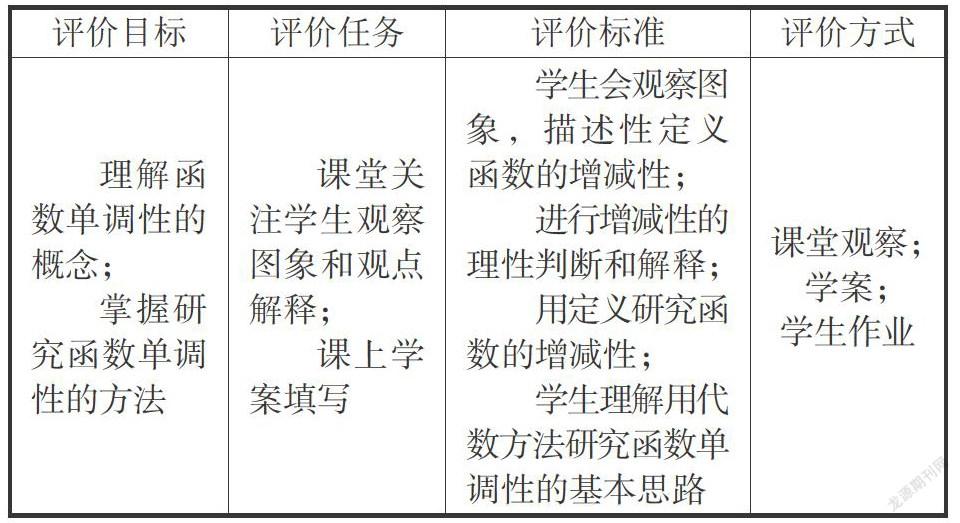
如何做好主题教学的发展性评价？一是评价教学目标是否达成，目标指向哪里，评价必须跟到哪里. 评价要关注学生在学习过程中的发展与变化，学生的知识掌握、数学理解、独立思考等都是随着学习过程的变化而发展的，是一种螺旋式的上升，只有评价学生的整个学习行为和思维过程，才能发现教学中的问题，进而及时调整，改进教学行为. 二是将评价任务置于教学目标和学习过程之间，使评价任务起到承上启下的作用，上接教学目标，以随时观测与目标的匹配性，下连学习过程，把评价融入教学过程，遵循教、学、评一致性的教学设计.

以函数单调性主题教学的第1课时“理解函数单调性的概念、掌握研究函数单调性的方法”为例，评价设计如下表所示.

综上，高中数学主题教学设计，从教学内容的确定上要把握学习知识、思想方法、学科素养的整体性;从学习目标的定位上要把握课程、主题、课时的结构性;从教学过程的实施上要把握由浅入深、由易到难的层次性;从教学评价的方式上要把握激励、动态的发展性. 数学学科核心素养导向下的主题教学设计是落实立德树人、发展素质教育、深化课程改革的必然要求，是数学学科核心素养落实于教学实践的关键途径，也是一个不断探索、学习、实践、创新的过程. 教师要立足自身专业成长，做到理解数学、理解学生、理解技术、理解教学，不断学习、反思总结、积累并開发主题教学设计的新资源.

参考文献：

[1]鲍怡. 高中数学函数单调性解题方法探讨[J]. 数理化学习（高一二版）2015（11）：11-12.

[2]房小骞. 分析函数的单调性在高中数学中的学习与应用[J]. 高考（下旬），2018（3）：46.

[3]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.

[4]崔允漷. 如何开展指向学科核心素养的大单元设计[J]. 北京教育（普教版），2019（2）：11-15.