基于功能度量法的桁架结构非概率可靠性拓扑优化方法研究
2021-09-07
(北京航空航天大学 航空科学与工程学院 固体力学研究所,北京 100191)
1 引 言
结构优化问题是指在满足给定的几何约束、材料约束和状态约束条件下,寻求使得给定目标最优的设计。结构优化可以分为三个层次,从低到高分别是尺寸优化、形状优化和拓扑优化。结构拓扑优化能够设计结构的拓扑构型,相比于尺寸优化和形状优化具有更加广泛的设计空间,因而能够取得更大的经济效益。桁架结构广泛应用于航空航天和土木工程领域,如卫星天线支撑结构和大跨度桥梁。随着数值优化方法和计算机科学的巨大进步,桁架结构的拓扑优化受到广泛研究并逐步应用到实际工程中[1-4]。值得注意的是,在大多数的研究中,结构的材料特性和外载荷假定为确定性的。
然而在实际工程中,材料性能的分散性以及外部载荷的波动可能会对结构的功能产生较大的影响。在这种情况下,提出了基于概率理论的可靠性拓扑优化设计,并得到了广泛的研究。陈建军等[5]对具有位移和应力概率可靠性约束的桁架结构拓扑优化问题进行了初步研究。Bae等[6]利用传统的一阶可靠度分析方法,对考虑弹性模量、厚度及荷载为概率分布不确定量的平面问题进行可靠度拓扑优化。Kharmanda等[7]提出以应变能最小化为目标的可靠度优化模型。Jung等[8]研究了三维几何非线性结构的概率可靠度拓扑优化问题。在实际工程中,Maute等[9]则对微电子机械系统(MEMS)进行了可靠性拓扑优化设计。
实际工程不易精确获得不确定性信息数据,但是对于不确定性信息的不确定界限却比较容易给出。基于这一思想,Ben-Haim[10]首次提出了基于凸集合模型的非概率可靠性概念。近年来,非概率可靠性理论得到了迅速的发展[11,12],基于非概率的可靠性拓扑优化的研究也取得了一定的进展。罗阳军等[13]考虑材料、几何及载荷大小的不确定性,提出了以结构体积最小化为目标,具有位移非概率可靠性约束的三维连续体拓扑优化数学模型。亢战等[14]利用凸模型理论,提出了改进的非概率可靠性指标定义,并针对桁架结构拓扑优化设计问题建立了以杆件截面积为设计变量和结构重量极小化为目标,具有非概率可靠性指标约束的广义尺寸优化数学模型。Wang等[15]考虑材料及载荷大小的不确定性,利用基于面积比的可靠性定义,研究了柔顺度约束下桁架结构的非概率可靠性拓扑优化问题。
本文利用基于面积比的可靠性定义,研究了柔顺度约束下桁架结构的非概率可靠性拓扑优化问题。与Wang等[15]的研究不同,Wang等[15]从几何上提出了偏移距离的概念,从而解决了原可靠性拓扑优化问题求解过程中存在的收敛性问题,而本文从代数的角度提出了功能度量法,完全从代数角度推导了目标功能度量的计算表达式,在这个过程中,采用了先计算再判定的策略。Wang等[15]采用的偏移距离方法在柔顺度许用值由区间退化为实数时不再适用,因为此时无法将实际柔顺度区间和柔顺度许用值区间表示在二维坐标系中,而本文提出的功能度量法是普适的。
本文采用区间模型来描述材料性质(弹性模量)和载荷大小的不确定性,利用参数顶点组合法来完成结构柔顺度上下界的计算,利用基于面积比的非概率可靠性定义构建了桁架结构的可靠性拓扑优化模型。提出了功能度量法,来解决原可靠性拓扑优化问题求解过程中存在的收敛性问题。最后,通过数值算例验证本文提出方法的有效性。
2 桁架结构拓扑优化问题描述
桁架结构在以体积为目标,柔顺度为约束下的拓扑优化问题可以表示为
s.t.F=Ku
C=FTu≤Cl
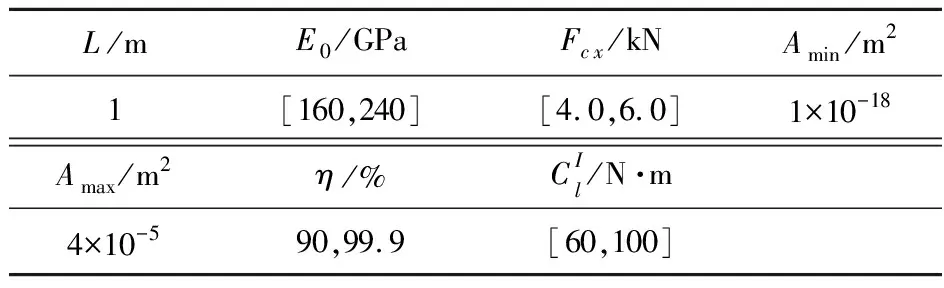
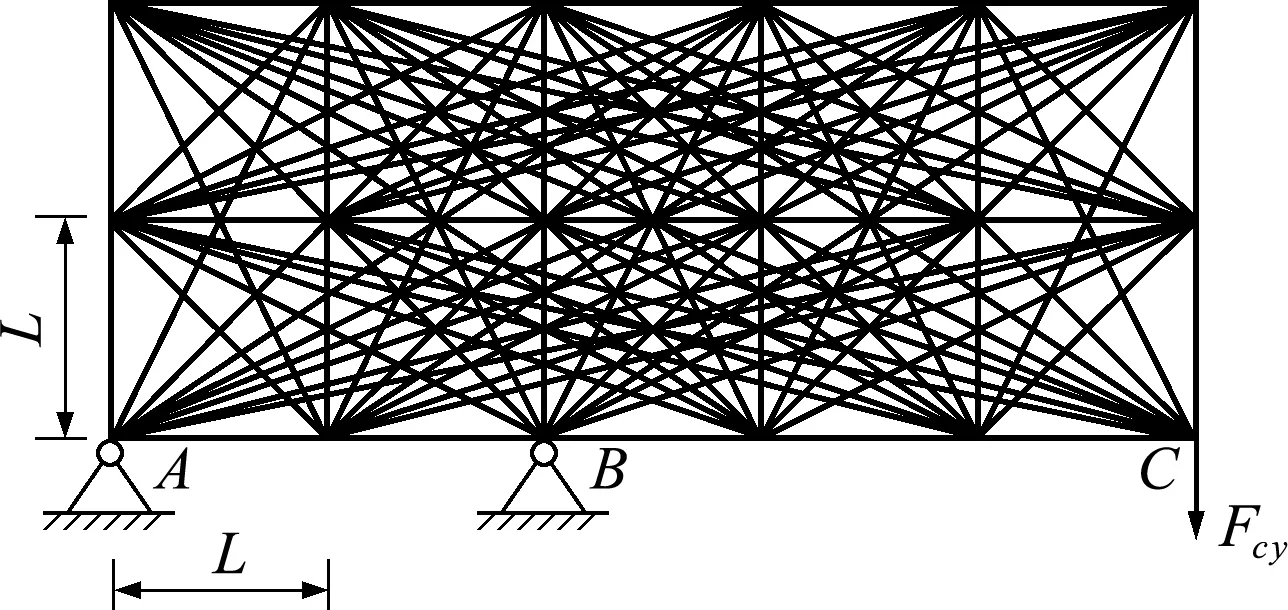
0 (1) 式中A=(A1,A2,…,AN)T表示设计变量,V为桁架结构的总体积,N为杆件的数量,Ak和Lk分别为第k个杆件的横截面积和长度,F为外载荷列向量,K为结构的总体刚度矩阵,u为结点位移列向量,C=FTu表示结构的柔顺度,体现了桁架结构在当前载荷下的总体刚度,Cl为结构柔顺度的许用值,Amin是为了避免刚度矩阵奇异而设置的下限,Amax为杆件容许最大横截面积。 利用杆件的容许最大横截面积,对设计变量进行如下处理, xk=Ak/Amax (2) 则式(1)的优化模型可以转化为 s.t.F=Ku C=FTu≤Cl 0 (3) 式中x=(x1,x2,…,xN)成为了新的设计变量。 传统的桁架结构拓扑优化是在假定结构材料参数和载荷参数是确定性参数下进行的,无法计及实际工程存在的不确定性影响。本文利用区间参数来描述材料弹性模量和外载荷大小的不确定性。区别于传统的概率模型,用概率密度函数来描述随机变量的特征,区间模型用参数的上下界来描述不确定性特征。通常,区间数可以表示为 (4) 当结构的材料参数(弹性模量)和外部载荷大小为区间量时,结构的响应也是区间量。由于结构柔顺度关于材料弹性模量和载荷大小是单调的,因此可以采用参数顶点组合法来确定结构柔顺度的上下界。当考虑区间不确定性时,结构静力方程为 KI(b)uI(b)=F (5) 式中b为不确定参数列向量。在不同的参数顶点下,进行静力有限元计算,然后计算结构的柔顺度值,则结构柔顺度的上下界可以从这些值的最大值和最小值得到。基于参数顶点组合法,结构的柔顺度上下界可以求解为 (6) 式中CI为结构柔顺度区间。 当计及不确定性的影响时,必须构建可靠性拓扑优化模型。桁架结构的非概率可靠性拓扑优化模型可以表示为 s.t.F=Ku Amin/Amax≤xk≤1 (k=1,…,N) (7) (8) 当结构的柔顺度上下界已知时,可以利用式(8)进行非概率可靠度计算,从而可以构建桁架结构非概率可靠性拓扑优化模型。 当采用梯度类优化算法直接求解式(7)的优化问题时,可能会存在收敛困难。因此,需要采取一定的转化策略对原可靠度进行等价转换。首先定义功能度量函数 (9) 图1 功能度量函数G (h)和功能度量h的关系 基于功能度量函数,原来的柔顺度可靠性约束可以表示为 (10) (11) 式中h*称为目标功能度量。基于式(10)的可靠性约束处理方式称为可靠性指标法,基于式(11)的可靠性约束处理方式称为功能度量法。 图2 可靠度指标法和功能度量法的比较 因此,本文采用功能度量法对结构柔顺度可靠性约束进行处理,则桁架结构非概率可靠性拓扑优化模型可以表示为 s.t.F=Ku h*≥0 Amin/Amax≤xk≤1 (k=1,…,N) (12) (13) (14) 当采用梯度类优化算法对桁架结构非概率可靠性拓扑优化问题进行求解时,需要计算目标功能度对设计变量的导数。 结合式(14),利用复合函数求导法则,目标功能度h*对第k个设计变量xk的灵敏度可求解为 (15) (16) 本文采用移动渐近算法(MMA)对优化问题进行求解。如图3所示,一个桁架结构在下面两个点A和B固定,在上面中间的点C有一个向右的集中载荷Fc x。假设材料的弹性模量以及集中力的大小为区间量。算例1相关参数的值列入表1。 图3 算例1桁架结构 表1 算例1相关参数的值 从图5可以看出,确定性优化和可靠性优化在最终的拓扑优化构型上有很大的不同,说明了在结构的概念设计阶段(拓扑优化)考虑不确定性影响是必要的。由图4和表2可知,可靠性优化结果的最终结构体积比确定性优化的最终结构体积大(可靠性优化为6.31×10-4m3和8.65×10-4m3;确定性优化为3.62×10-4m3),说明要提高结构的可靠性,需要采用更多的材料。另外,确定性优化结果在材料弹性模量、载荷大小以及柔顺度许用值为区间值时计算的实际柔顺度可靠度仅为37.53%,而可靠性优化结果的实际柔顺度可靠度都能满足设定的阈值,证明本文提出方法的有效性,也进一步说明了传统的确定性优化可能会使结构面临较大失效风险,因此在结构优化中必须考虑不确定性的影响。在文献[15]第一个算例中,可靠度为90%的优化结果不对称,这不符合实际情况,因为加载点位于对称位置且杆件拉压弹性模量一致,所以得到的结果理论上是对称的(文献[15]确定性优化结果也是对称的)。本文的可靠性优化结果都是对称的,与实际相符。推测可能是算法(本文采用MMA算法,文献[15]采用SQP算法)和转化方法(本文采用功能度量法,文献[15]采用偏移距离方法)的不同引起的。 图4 算例1中不同优化策略下的结构体积迭代历程曲线 图5 算例1中不同优化策略下的结构最终拓扑优化构型 表2 算例1中不同优化策略下的优化结果 如图6所示,底端A和B两点固定,在底端C点加载一个竖直向下的载荷。表3列举出了算例2相关参数的值。 图6 算例2中桁架结构 表3 算例2中相关参数的值 采用本文提出的方法分别在两种不确定性大小(α=0.1和α=0.2)下进行可靠性优化,并且将确定性优化的结果作为对比,得到的结果如图7和表4所示。 图7 算例2中不同优化策略下的结构最终拓扑优化构型 表4 算例2中不同优化策略下的优化结果 由图7和表4的结果可知,当不确定性较小时(α=0.1),可靠性拓扑优化结果与确定性优化结果差别较小;当不确定性较大时(α=0.2),可靠性拓扑优化结果与确定性优化结果有较大的差别。由 表4 可知,可靠性拓扑优化结果的结构实际柔顺度可靠度大于阈值(95%),证明了提出方法的有效性。另外,可靠性拓扑优化结果的结构体积要大于确定性拓扑优化结果的结构体积,并且随着不确性的增大,结构的体积也相应增加(α=0.1:8.59×10-4m3→α=0.2:1.2×10-3m3)。 本文研究了桁架结构的非概率可靠性拓扑优化问题。运用区间模型来描述结构材料参数(弹性模量)和载荷大小的不确定性,采用参数顶点组合法来求解结构柔顺度的上下界,运用基于面积比的可靠性指标构建桁架结构的非概率可靠性拓扑优化模型。针对原来的可靠性约束梯度信息在某些区域为0的情况,提出了功能度量法,将可靠度约束转化为目标功能度量的约束,从而解决了收敛性问题。进一步推导了目标功能度量的计算方法及其对设计变量的灵敏度。采用移动渐近方法(MMA)对优化问题进行求解。数值算例表明,所提功能度量法能够很好地解决桁架结构的非概率可靠性拓扑优化问题。另外,不确定性对结构最终拓扑优化构型有着较大的影响,在拓扑优化中考虑不确定性的影响是十分必要的。 参考文献(References): [1] Bendsøe M P,Ben-Tal A,Zowe J.Optimization methods for truss geometry and topology design[J].StructuralOptimization,1994,7(3):141-159. [2] Achtziger W,Bendsøe M P.Optimal topology design of discrete structures resisting degradation effects[J].StructuralOptimization,1999,17(1):74-78. [3] Achtziger W,Stolpe M.Truss topology optimization with discrete design variables—Guaranteed global optimality and benchmark examples[J].StructuralandMultidisciplinaryOptimization,2007,34(1):1-20. [4] Guo X,Cheng G D.A new approach for the solution of singular optimum in structural topology optimization[J].ActaMechanicaSinica,1997,13(2):171-178. [5] 陈建军,曹一波.基于可靠性的桁架结构拓扑优化设计[J].力学学报,1998,30(3):277-284.(CHEN Jian-jun,CAO Yi-bo,DUAN Bao -yan.Topology optimization of truss structures based on reliability [J].ActaMechanicaSinica,1998,30(3):277-284.(in Chinese)) [6] Bae K R,Wang S.Reliability-based topology optimization[A].9t hAIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization[C].2013. [7] Kharmanda G,Olhoff N,Mohamed A,et al.Reliabi-lity-based topology optimization[J].StructuralandMultidisciplinaryOptimization,2004,26(5):295-307. [8] Jung H S,Cho S.Reliability-based topology optimization of geometrically nonlinear structures with loa-ding and material uncertainties[J].FiniteElementsinAnalysisandDesign,2004,41(3):311-331. [9] Maute K,Frangopol D M.Reliability-based design of MEMS mechanisms by topology optimization[J].Computers&Structures,2003,81(8-11):813-824. [10] Ben-Haim Y.A non-probabilistic concept of reliability[J].StructuralSafety,1994,14(4):227-245. [11] Wang X J,Qiu Z P,Elishakoff I.Non-probabilistic set-theoretic model for structural safety measure[J].ActaMechanica,2008,198(1-2):51-64. [12] 曹鸿钧,段宝岩.基于凸集合模型的非概率可靠性研究[J].计算力学学报,2005,22(5):546-550.(CAO Hong-jun, DUAN Bao -yan.An approach on the non-probabilistic reliability of structures based on uncertainty convex models[J].ChineseJournalofComputationalMechanics,2005,22(5):546-549,578.(in Chinese)) [13] 罗阳军,亢 战,蔡 坤.考虑非概率可靠性的结构柔顺度拓扑优化设计[J].计算力学学报,2011,28(6):821-826.(LUO Yang-jun,KANG Zhan,CAI Kun.A compliance based topology optimization design of structures considering non-probabilistic reliability[J].ChineseJournalofComputationalMechanics,2011,28(6):821-826.(in Chinese)) [14] 亢 战,罗阳军.桁架结构非概率可靠性拓扑优化[J].计算力学学报,2008,25(5):589-594.(KANG Zhan,LUO Yang-jun.Topology optimization of truss structures for non-probabilistic reliability[J].ChineseJournalofComputationalMechanics,2008,25(5):589-594.(in Chinese)) [15] Wang L,Liu Y S,Yang Y W.Truss layout design under non-probabilistic reliability-based topology optimization (NRBTO) framework with interval uncertainties[J].InternationalJournalforNumericalMethodsinEngineering,2019,119(12):1307-1324.3 桁架结构非概率可靠性拓扑优化
3.1 区间模型

3.2 结构响应传播分析
3.3 非概率可靠性拓扑优化模型

4 求解策略
4.1 基于功能度量法的可靠度约束转换





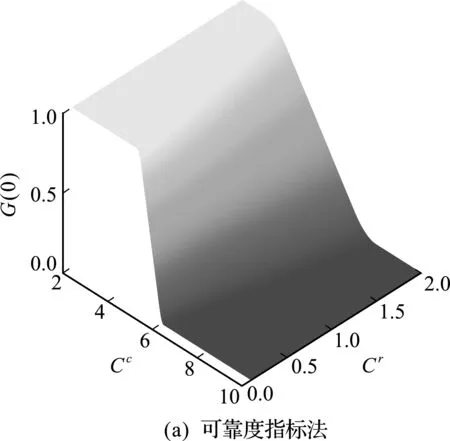

4.2 目标功能度量求解

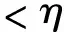

4.3 目标功能度量的灵敏度求解
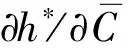
5 数值算例
5.1 算例1
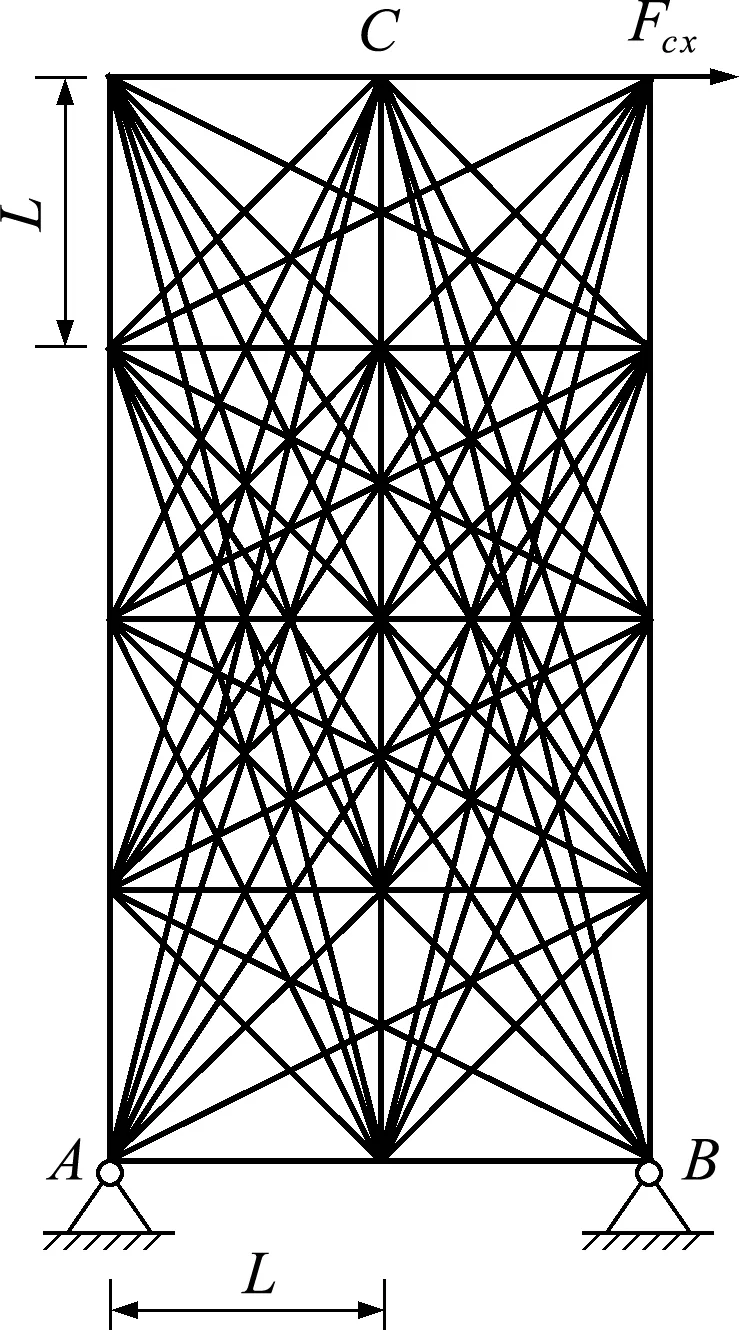



5.2 算例2



6 结 论
