形状记忆合金结构拓扑优化设计方法研究

223 张卫红2

(1.西北工业大学 航宇材料结构一体化设计与增材制造装备技术国际联合研究中心，西安 710000；2.西北工业大学 金属高性能增材制造与创新设计工信部重点实验室，西安 710000；3.西北工业大学 无人系统技术研究院-智能材料与结构研究所，西安 710000；4.中国工程物理研究院 激光聚变研究中心，绵阳 621900)

1 引 言

形状记忆合金SMA(Shape Memory Alloy)是一种先进的智能材料，其在不同的热力载荷下会呈现出两种不同的独特性能,(1) 形状记忆效应SME(Shape Memory Alloy)，在外载荷单次加卸载作用下SMA材料产生塑性残余变形，通过升高材料温度，残余变形可以完全恢复；(2) 伪弹性性能PE(Pseudoelasticity)，SMA材料在受到外载荷作用时，可以发生高达6%～8%的显著应变而不进入屈服状态，卸除外载后结构形状完全恢复，并在这个过程耗散大量的能量[1]。几十年来，相关学者提出了众多关于SMA材料的微观、微观-宏观以及宏观本构模型[2]。微观模型主要是描述晶格或晶粒尺度上的结构特征，如晶核生长、界面运动和马氏体孪晶生长等。微观-宏观模型通过微观力学来描述微观或介观尺度上的材料行为，再通过尺度转换获取宏观尺度上的本构方程。宏观模型基于唯象学、简化的微观-宏观热力学或直接的实验数据拟合来描述材料行为。其中，宏观模型具有参数少和容易实验标定的特点，适合在结构尺度上对材料的力学响应进行分析。

SMA由于其优良的力学特性而在工程应用中获得了广泛关注，并形成了一系列具有变革性的创新应用，如智能变形机翼[3]、矫正装置[4]和减震阻尼元件[5]等。为了简化设计和制造过程，SMA材料往往以丝材、棒材和板材等简单形式在结构中使用，限制了SMA结构性能的进一步提升。随着增材制造技术的发展，研发出具有良好形状记忆效应和伪弹性性能的复杂SMA结构[6,7]，意味着SMA结构的设计将获得更多自由度。因此，扩展面向SMA结构的设计方法，以充分利用SMA材料独特的力学性能，是一个有前景的研究方向。

结构优化技术是一种先进的设计方法，广泛应用在航空航天、汽车、船舶和装备制造等工程领域[8,9]。在Bendsøe等[10]提出均匀化方法之后，拓扑优化技术得到了迅猛发展。在均匀化的基础上，Bendsøe[11]又提出了基于密度变量法的固体各向同性材料插值模型(SIMP)，进一步完善了拓扑优化方法。为了避免棋盘格现象和网格依赖性[12]，文献[13，14]分别在SIMP变密度方法中引入了灵敏度过滤技术和密度过滤技术，但这也在最终结果中导致了大量的中间密度单元。通过对过滤密度进一步投影，形成三密度场[15](设计密度场、过滤密度场和物理投影密度场)，可以获得清晰的结构。目前，SMA的结构设计往往基于启发式思想，关于SMA结构优化设计的研究并不多见。Hartl等[16]在SMA驱动的可变形结构研究中，采用一种新的本构模型对整体可变形结构进行了参数优化，得到满足刚度、驱动偏转角度和应力水平等约束的最小质量设计方案。马彦等[17]采用遗传算法对SMA管接头进行了优化设计，提升了管接头的连接性能。Gu等[18]在SMA自支撑支架的设计中，考虑SMA的疲劳性能，通过参数优化将最大疲劳因子降低了25%，显著提升了结构抗疲劳性能。Langelaar等[19]利用SMA的伪弹性，使用基于镍钛基形状记忆合金R相变的简化本构模型，开展了SMA作动器的拓扑优化设计，获得了多种作动器结构的拓扑形式。

SMA结构在实际应用中往往会产生较大变形，且会发生马氏体与奥氏体之间的相互转变，因此需要考虑几何非线性和材料非线性。而在考虑非线性效应的变密度拓扑优化方法中，由低密度单元引起的非线性分析数值不稳定问题是优化过程中的一个主要障碍。为了解决这个问题，相关学者提出了多种方法。Bruns等[20]提出了一种单元去除和重新引入的策略。Wang等[21]提出了能量插值法，对实体单元区域和低密度单元区域的分析分别应用非线性列式和线性列式来改善分析的收敛性。Luo等[22]提出了扩展的移动等值面阈值法MIST(moving iso-surface threshold)。Hou等[23]基于超单元法，将低密度单元凝聚成超单元以避免单元的过度扭曲。考虑到计算效率，同时为了利用商业软件完成有限元分析，本文使用超单元法来改善非线性效应引起的数值问题。

本文提出了一种适用于形状记忆合金结构的变密度拓扑优化方法。采用ZM宏观唯像本构模型，并同时考虑材料非线性和结构的几何非线性。使用SIMP模型对SMA材料进行插值，以建立密度设计变量和材料性能之间的映射关系。采用三密度场法来避免优化结果中出现的棋盘格现象、网格依赖性以及大量中间密度单元；采用超单元法来改善优化过程的数值不稳定问题；使用伴随法准确获取优化模型中响应函数的灵敏度。最后，通过两组算例验证本文提出的SMA结构拓扑优化设计方法的有效性。

2 形状记忆合金材料模型和有限元分析

2.1 ZM本构模型

本文使用的形状记忆合金本构模型是Zaki等[24]提出的ZM宏观唯象本构模型。ZM模型采用六个状态变量描述SMA的力学行为，分别是宏观应变张量ε、局部奥氏体应变张量εA、局部马氏体应变张量εM、马氏体体积分数z、马氏体取向应变张量εtr以及温度T。

通过上述变量，定义Helmholtz自由能和上述变量的内约束，构造拉格朗日函数，定义状态方程[24]，可得到应力应变关系如下，

σ=K∶(ε-zεtr)

(1)

式中K为SMA的等效弹性张量，可以表示为

(2)

式中KA为奥氏体弹性张量，KM为马氏体弹性张量。

ZM模型中定义伪耗散势为

(3)

式中a，b以及Y为材料参数。

在广义标准材料体系下，伪耗散势的次梯度是耗散变量的驱动力，

(4，5)

(6)

(7)

(8)

最终，由式(6～8)可得到流动法则如下，

(9)

(10)

(11)

2.2 非线性有限元分析

在有限元分析中，非线性有限元问题可以表示为残量的形式，

R=Fint-F=0

(12)

(13)

(14)

式中B为几何矩阵，N为形状函数矩阵，Fint为内力，F为外力，其包含体力b以及面力t。

整体的有限元分析采用NR迭代法，在NR迭代中需要使用到的切向刚度矩阵定义为

KT=-∂R/∂u

(15)

3 拓扑优化模型

3.1 材料插值模型

在经典变密度拓扑优化算法中，设计域首先要离散为一定数目的有限单元，并用单元赋予的密度变量xe来表示第e个单元上材料的有无(xe=1表示此处存在材料，xe=0表示此处无材料)。为了使问题能够基于梯度的优化算法解决，需要拓展原始的离散状态问题，建立密度变量与材料属性之间的连续映射关系。本文采用的SIMP模型是一种广泛应用于拓扑优化的材料插值模型，其基本思想是使用惩罚后的密度变量对材料的力学性能进行插值，继而通过优化算法实现材料分布的优化设计。

(16)

式中EA 0，EM 0，σm s 0，σm f 0，σa s 0和σa f 0分别为实体单元的奥氏体弹性模量、马氏体弹性模量以及四个相变转变应力，Emin=1×10-9，σmin=1×10-9，P是惩罚因子。

使用上述材料插值模型得到的不同密度变量下材料的伪弹性本构曲线如图1所示。可以看出，在P=1的情况下，材料的弹性模量和转变应力随着密度变量的减小而线性减小。应力应变曲线围成的滞回环面积代表了发生完全相变的SMA材料所耗散的能量密度。密度变量为1.0， 0.5和0.1的材料对应的耗散能量密度分别为4.56×106J/m3，2.28×106J/m3和4.56×105J/m3，与密度变量呈线性关系。

图1 不同密度材料对应的SMA伪弹性本构曲线

3.2 三密度场法

(17)

式中vj为单元j的体积，we j为加权函数值，其计算方法如下，

(18)

式中Xe为单元e的中心坐标。

(19)

3.3 超单元方法

本文采用超单元法[23]对低密度材料区域的有限元节点自由度进行凝聚，以改善弱材料单元导致的数值不稳定问题，如图2所示。

图2 超单元的定义

(20)

式(20)左边的刚度矩阵均基于线弹性理论，不需要考虑几何非线性效应。由式(20)可得

(21)

(22)

式中

(23)

当分析实体单元区域时，采用增量形式的NR迭代求解平衡状态，对于第N个载荷步的第t+1次迭代，区域p1内位移与载荷的关系可以表示为

(24)

考虑实体单元区域与弱单元区域边界自由度的影响，平衡方程改写为

(25)

3.4 优化模型数学表述

本文通过对伪弹性条件下的SMA结构进行刚度优化来验证优化方法的有效性。为了得到合理的结构，还需要施加材料用量的约束。因此，该拓扑优化问题可以定义为在满足最大体积分数约束的情况下，最小化SMA结构的平衡状态柔顺度Cend。用数学公式可表示为

minCend

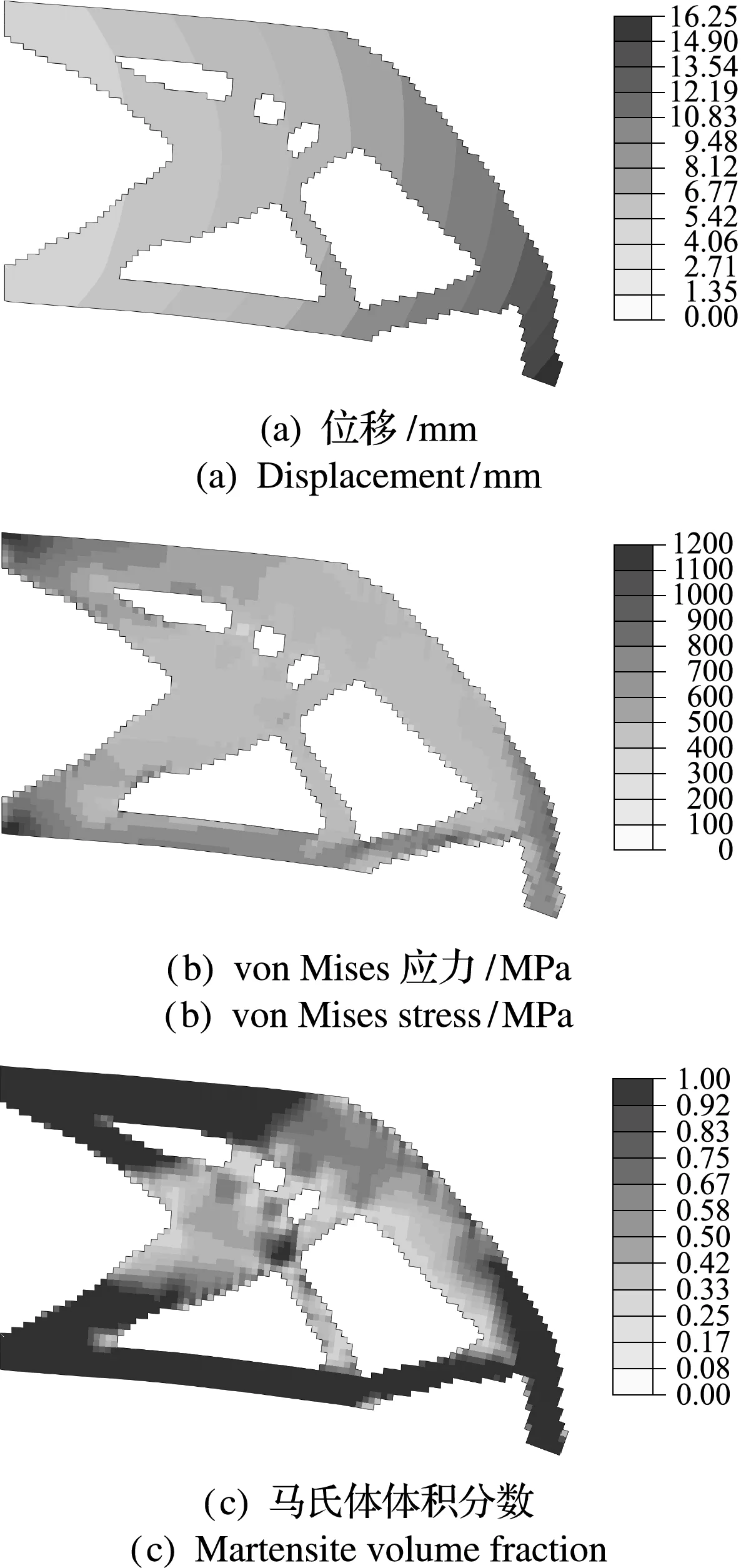
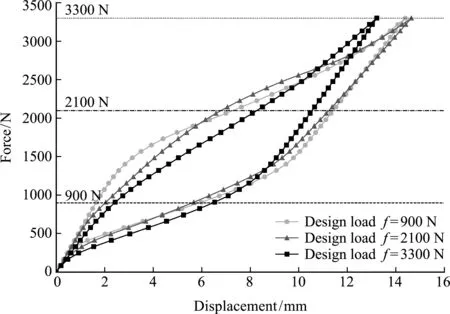
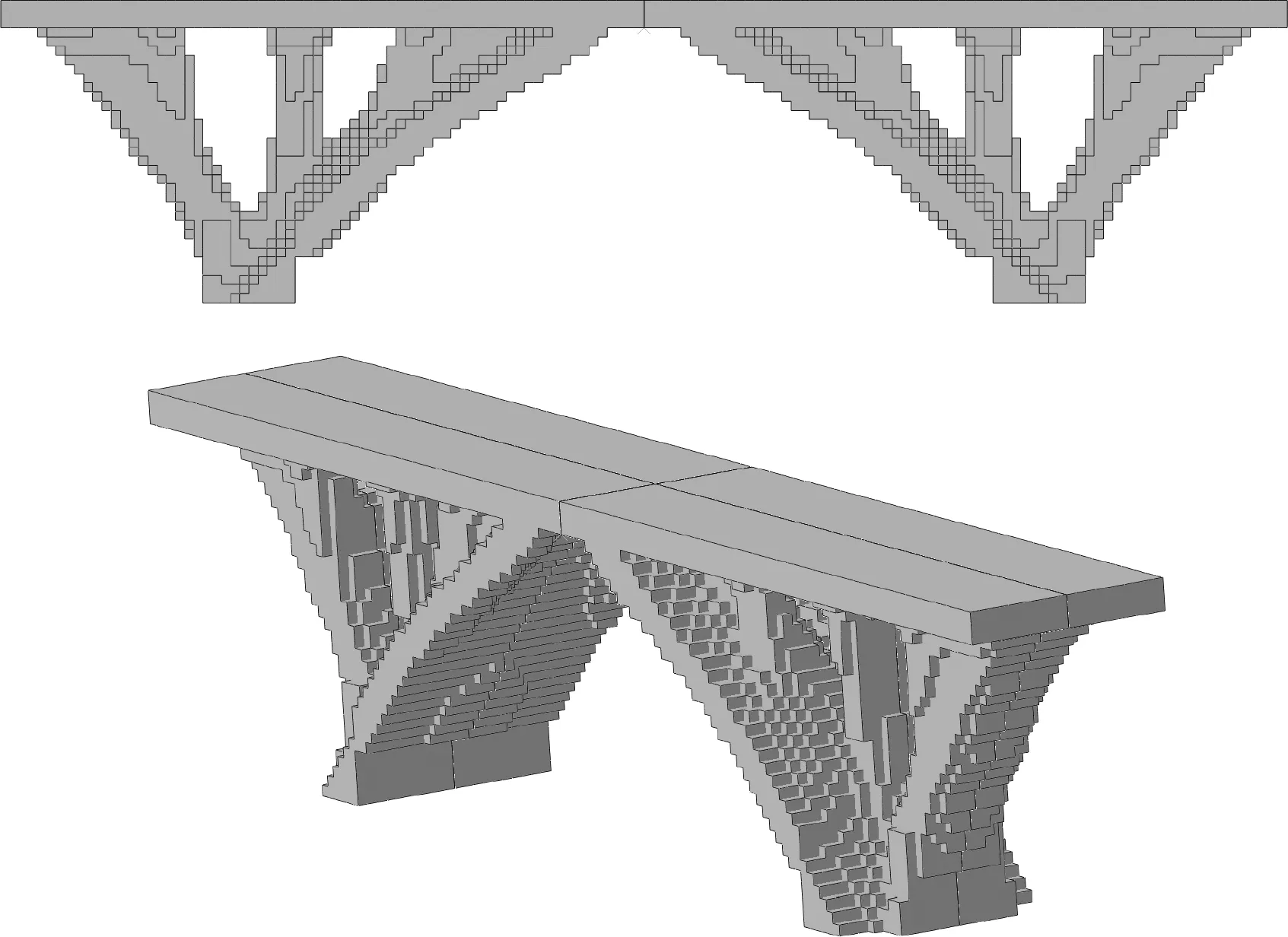
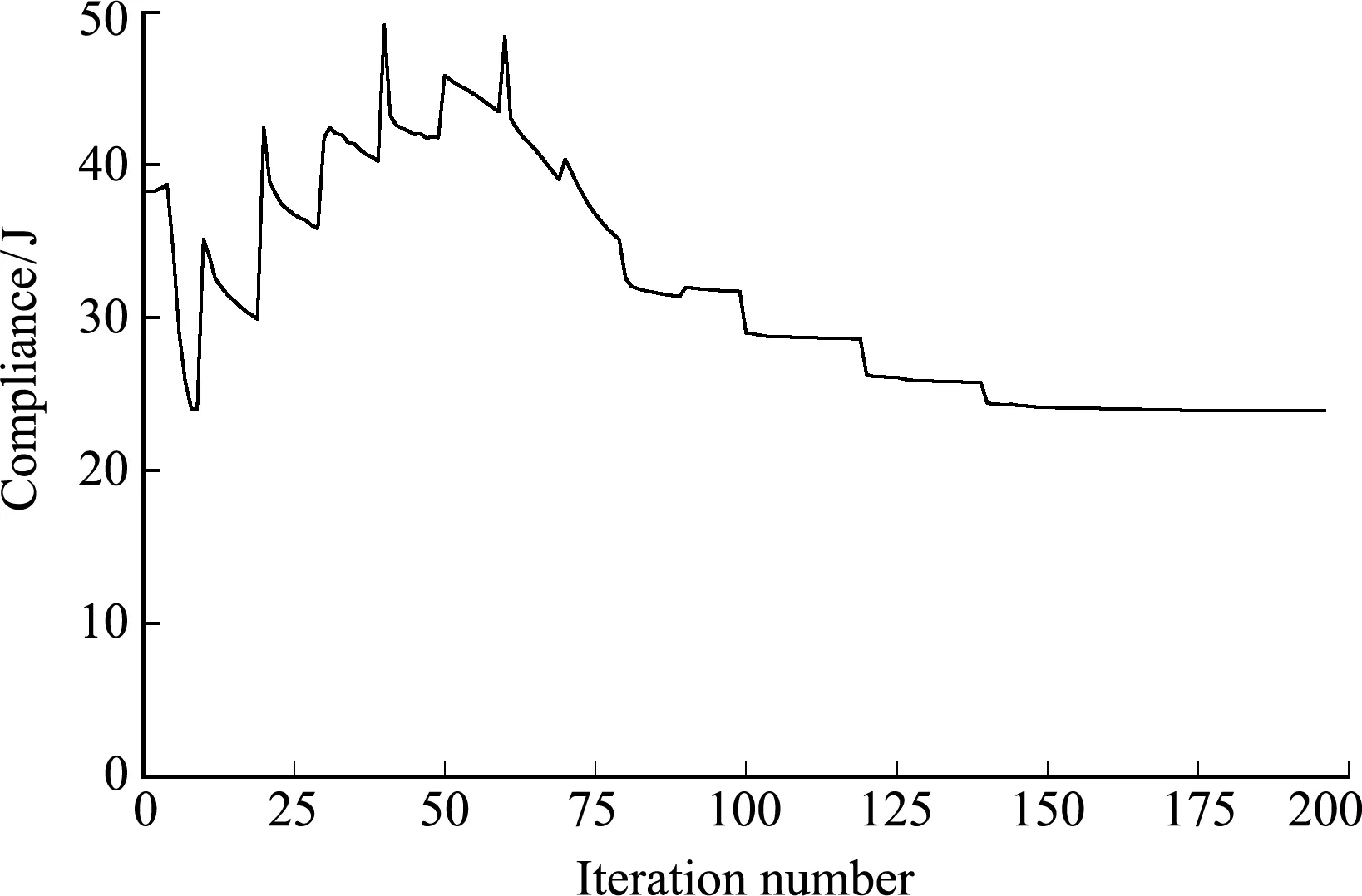
0

(26)

式中ve为对应单元的体积，V为设计域的总体积，Vf为体积分数约束的数值，ne l e为设计域的总单元数，xmin=1×10-3。

最终状态柔顺度Cend为

(27)

式中Fmax为加载结束时的外力，umax为对应的位移。

4 灵敏度分析

在优化过程中，需要计算出响应函数对设计变量的灵敏度以不断更新结构。直接法和伴随法是两种常见的计算方法。在拓扑优化问题中，设计变量数通常远大于目标和约束数，因此，伴随法在灵敏度分析中更有效率。本文使用伴随法对平衡状态柔顺度的灵敏度进行推导。

平衡状态柔顺度Cend关于设计变量的灵敏度可表示为

(28)

(29)

式中Rend为加载过程中最后一个增量步的残量。由于结构处于平衡状态时Rend=0，因此改写之后的目标函数值在平衡状态不发生变化。

(30)

式中

∂Rend/∂umax=-KT,end

(31)

式中KT,end为加载过程中最后一步的切线刚度矩阵。

(32)

记第N步和第N-1步的位移分别为uN和uN - 1。假设在一个小的增量步中力-位移关系是线性的，则力在第N-1步至第N步的增量可以近似地表示为

KT,end(uN-uN - 1)=Fmax/N

(33)

(34)

综上，最终状态柔顺度关于设计变量的灵敏度可表示为

(35)

因外力Fmax与设计变量x无关，结合式(12，35)，可将最终状态柔顺度关于设计变量的灵敏度简化为

(36)

5 数值算例

采用一些数值算例来验证提出的形状记忆合金拓扑优化设计方法的有效性。材料参数列入 表1。利用商业有限元软件Abaqus完成有限元分析，SMA材料在用户材料子程序UMAT (user material subroutine)中定义。采用GCMMA(Glo -bally Convergent Method of Moving Asymptotes)[25]算法来求解优化问题。

表1 优化计算时的材料参数

5.1 SMA悬臂梁结构优化设计问题

算例1考虑SMA悬臂梁结构的拓扑优化设计问题，其初始的几何形状与尺寸如图3所示，厚度为1 mm。结构左侧固定，在右下角宽为5 mm的区域内施加3300 N的载荷。设计域离散为 50×100个单元，单元在平面内的尺寸为 1 mm×1 mm。体积分数设置为Vf=0.5。过滤半径取单元尺寸的3倍。惩罚因子P在优化的初始阶段为1，最大值设置为3，每10个迭代步增加 0.16。Heaviside投影的参数β0在第1个迭代步等于1，之后每20个迭代步增大1.4倍，直至其等于24。

图3 悬臂梁设计域

图4展示了SMA悬臂梁结构的材料分布演变过程。经过248步迭代，拓扑优化算法得到一个清晰的优化解。最终设计方案的位移云图、 Mises 应力云图以及马氏体体积分数云图如图5所示，平衡状态柔顺度由初始的52.69 J降低至44.95 J，减少约15%。优化过程平稳收敛，优化的迭代历史如图6所示。在0至100步之间存在明显的阶跃台阶，这是由惩罚因子P的增加所引起的中间密度材料刚度惩罚加剧导致。平衡状态柔顺度的数值在100步至200步之间偶尔出现震荡，这是因为在优化过程中结构的局部区域会因刚度较弱而发生非线性屈曲。但随着优化的继续进行，这些区域的刚度得到加强，柔顺度数值趋于稳定。

图4 SMA悬臂梁刚度优化设计历史

如图5(a)所示，最终的优化结构在外力载荷的作用下发生了较大的变形，最大位移达到 16.25 mm，是结构竖直方向尺寸的30%，可以证明本文的方法在处理大变形的拓扑优化设计问题时仍具有较好的稳健性。从图5(b，c)可以看出，在悬臂梁的根部和加载区域应力数值较大，相应地，这些区域的马氏体体积分数z=1，发生了完全马氏体相变，材料的总应变ε由奥氏体应变εA、马氏体取向应变εtr以及定向马氏体应变εM组成；结构中部区域发生了部分马氏体相变，此时有0

图5 SMA悬臂梁优化结构的力学响应

图6 SMA悬臂梁优化迭代历史

为了进一步说明本优化方法的有效性，图7分别列出了设计载荷为900 N和2100 N的情况下悬臂梁的刚度优化结果，并与图4设计载荷为3300 N的优化结果进行对比。可以看出，随着载荷的增加，结构形式发生较大变化，加载位置出现短梁直接承受拉力。图8给出了优化结构在相应的设计载荷下的位移云图、Mises应力云图以及马氏体相变云图。其中，在设计载荷为900 N的情况下，相应的优化结构变形较小，且基本不会发生马氏体相变，优化受非线性效应影响不大，与线弹性材料的拓扑优化结果类似。

图7 不同载荷下悬臂梁刚度优化结果

图8 不同设计载荷下优化构型的力学响应

图9绘制了设计载荷分别为900 N，2100 N和3300 N的优化结构在加载-卸载过程中的力-位移曲线。当实际载荷在900 N左右时，图7(a)的结构刚度明显较好；当实际载荷在2100 N左右时，图7(b)的结构在这三种结构中刚度最好；当实际载荷达到3300 N时，图4结构的刚度明显优于其他两种结构。观察图9曲线可以看出，结构的刚度整体呈先减小后增大的趋势。在载荷较大的情况下，如达到3300 N时，尽管部分材料已经完全转变为马氏体(图5(c))，但考虑SMA材料特性的结构拓扑设计方案可以很好地抵消材料相变导致的结构刚度损失。

图9 不同设计载荷下优化构型的力-位移曲线

5.2 SMA三维桥梁优化设计问题

算例2考虑一个三维SMA桥梁结构的拓扑优化问题，其初始几何形状和尺寸如图10所示。在上表面均匀施加133.88 MPa的压力，载荷施加面下方3 mm厚的区域设置为非设计域，设计域及非设计域均为SMA材料。设计域下方凸墩的下表面固定。因结构的对称性，只取1/4结构进行优化设计。设计域离散为18000个1 mm×1 mm×1 mm 的六面体实体单元。体积分数设置为Vf=0.2。过滤半径取单元尺寸的3倍。惩罚因子P在优化的初始阶段为1，之后每10个迭代步增加 0.2，直到P=3。Heaviside投影的参数β0在第1个迭代步等于1，之后每20个迭代步增大1.5倍，直至其等于16。

图10 三维桥梁设计域

经过196步，拓扑优化算法寻找到一个清晰的优化解，设计结果如图11所示。最终设计方案的位移云图、Mises应力云图以及马氏体相变云图如图12所示，平衡状态柔顺度由初始的38.30 J降低至23.91 J，减少约38%。优化的迭代历史如 图13 所示，整体优化过程收敛平稳，平衡状态柔顺度仅在惩罚因子P发生改变的迭代步之后几步发生一些跳动。

图11 三维桥梁刚度优化结果

如图12(a)所示，最大位移发生在桥面中心以及两端的局部区域内，这是因为优化目标是整体结构的平衡状态柔顺度最大，结构的局部刚度可能出现过弱的情况。从图12(b)可以看出，由于拓扑优化算法只是为了寻找一个刚度最优的结构，所以也会导致局部应力较为集中。除了桥面局部刚度较弱的区域因大变形而导致较大应力外，凸墩上方区域也因传力集中而产生了较大应力。相应地，这些区域的材料在外力的作用下发生了完全马氏体相变，而其他区域未发生相变或仅发生了局部相变，如图12(c)所示。

图12 三维SMA桥梁优化结构的力学响应

图13 三维SMA桥梁优化迭代历史

6 结 论

本文提出了一种基于SIMP模型的SMA结构拓扑优化设计方法，使用ZM宏观唯象本构模型以获得准确的力学响应，并对马氏体和奥氏体弹性模量以及四个转变应力进行插值以建立起密度设计变量和材料属性之间的映射关系。除了材料非线性效应外，还考虑了大变形引起的几何非线性效应，并通过超单元法改善了非线性有限元分析中的数值不稳定问题。响应函数的灵敏度通过伴随法求出。分别通过二维和三维的SMA结构优化数值算例表明本文方法可以有效地对预期性能的SMA结构进行优化设计。本文工作搭建了一个面向SMA结构的拓扑优化框架，能够作为进一步开展SMA智能变体结构、缓冲吸能结构和阻尼结构等优化设计的基础。

参考文献(References):

[1] Otsuka K,Wayman C M.ShapeMemoryMaterials[M].Cambridge:Cambridge University press,1998.

[2] Cisse C,Zaki W,Ben Zineb T.A review of constitutive models and modeling techniques for shape memory alloys [J].InternationalJournalofPlasticity,2016,76:244-284.

[3] 冷劲松,孙 健,刘彦菊.智能材料和结构在变体飞行器上的应用现状与前景展望 [J].航空学报,2014,35(1):29-45.(LENG Jin-song,SUN Jian,LIU Yan-ju.Application status and future prospect of smart materials and structures in morphing aircraft [J].ActaAeronauticaetAstronauticaSinica,2014,35(1):29-45.(in Chinese))

[4] 刘晓鹏.NiTi形状记忆合金的超弹性及医学应用研究[D].大连理工大学,2008.(LIU Xiao -peng.Study of Superelasticity of NiTi Shape Memory Alloy and Biomedical Applications [D].Dalian University of Technology,2008.(in Chinese))

[5] 李 惠,刘金龙,马 赫,等.基于OpenSees平台的SMA被动阻尼器及其在斜拉桥减震中的应用[J].计算力学学报,2009,26(3):374-378,400.(LI Hui,LIU Jin-long,MA He,et al.Control on nonlinear seismic response of cable -stayed bridge using SMA damper based on OpenSees [J].ChineseJournalofComputationalMechanics,2009,26(3):374-378.400.(in Chinese))

[6] Moghaddam N S,Saedi S,Amerinatanzi A,et al.Achieving superelasticity in additively manufactured NiTi in compression without post-process heat treatment [J].ScientificReports,2019,9:41.

[7] Wang X B,Yu J Y,Liu J W,et al.Effect of process parameters on the phase transformation behavior and tensile properties of NiTi shape memory alloys fabricated by selective laser melting [J].AdditiveManufacturing,2020,36:101545.

[8] Deaton J D,Grandhi R V.A survey of structural and multidisciplinary continuum topology optimization:Post 2000 [J].StructuralandMultidisciplinaryOptimization,2014,49(1):1-38.

[9] 王 斌.结构多性能优化设计及其在航天结构设计中的应用[D].大连理工大学,2010.(WANG Bin.Multi-performance Optimization of Structures and its Application in Aerospace Structural Design [D].Dalian University of Technology,2010.(in Chinese))

[10] Bendsøe M P,Kikuchi N.Generating optimal topologies in structural design using a homogenization method [J].ComputerMethodsinAppliedMecha-nicsandEngineering,1988,71:197-224.

[11] Bendsøe M P.Optimal shape design as a material distribution problem [J].StructuralOptimization,1989,1(4):193-202.

[12] Sigmund O,Petersson J.Numerical instabilities in topology optimization:A survey on procedures dealing with checkerboards,mesh-dependencies and local minima [J].StructuralOptimization,1998,16(1):68-75.

[13] Sigmund O.Design of Material Structures Using Topology Optimization [D].Copenhagen:Technical University of Denmark,1994.

[14] Bourdin B.Filters in topology optimization [J].InternationalJournalforNumericalMethodsinEngineering,2001,50(9):2143-2158.

[15] Sigmund O,Maute K.Topology optimization approaches:A comparative review [J].StructuralandMultidisciplinaryOptimization,2013,48(6):1031-1055.

[16] Hartl D J,Lagoudas D C,Calkins F T.Advanced methods for the analysis,design,and optimization of SMA-based aerostructures [J].SmartMaterialsandStructures,2011,20(9):094006.

[17] 马 彦,李 威.形状记忆合金管接头结构优化与有限元分析 [J].东北大学学报(自然科学版),2013,34(8):1166-1170.(MA Yan,LI Wei.Structure optimization and finite element analysis of shape memory alloy coupling [J].JournalofNortheasternUniversity(NaturalScience),2013,34(8):1166-1170.(in Chinese))

[18] Gu X J,Cao Y F,Zhu J H,et al.Shape optimization of SMA structures with respect to fatigue [J].Materials&Design,2020,189:108456.

[19] Langelaar M,Yoon G H,Kim Y Y,et al.Topology optimization of planar shape memory alloy thermal actuators using element connectivity parameterization [J].InternationalJournalforNumericalMethodsinEngineering,2011,88(9):817-840.

[20] Bruns T E,Tortorelli D A.An element removal and reintroduction strategy for the topology optimization of structures and compliant mechanisms [J].InternationalJournalforNumericalMethodsinEngi-neering,2003,57(10):1413-1430.

[21] Wang F W,Lazarov B S,Sigmund O,et al.Interpolation scheme for fictitious domain techniques and topology optimization of finite strain elastic problems [J].ComputerMethodsinAppliedMechanicsandEngineering,2014,276:453-472.

[22] Luo Q T,Tong L Y.An algorithm for eradicating the effects of void elements on structural topology optimization for nonlinear compliance [J].StructuralandMultidisciplinaryOptimization,2016,53:695-714.

[23] Hou J,Gu X J,Zhu J N,et al.Topology optimization of joint load control with geometrical nonlinearity [J].ChineseJournalofAeronautics,2020,33(1):372-382.

[24] Zaki W,Moumni Z.A three -dimensional model of the thermomechanical behavior of shape memory alloys [J].JournaloftheMechanicsandPhysicsofSo-lids,2007,55(11):2455-2490.

[25] Svanberg K.A class of globally convergent optimization methods based on conservative convex separable approximations [J].SocietyforIndustrialandApp-liedMathematics,2002,12(2):555-573.