结构拓扑优化局部性能约束下轻量化问题的互逆规划解法

隋允康， 彭细荣*2， 叶红玲， 李宗翰

(1.北京工业大学 材料与制造学部，北京 100022; 2.湖南城市学院 土木工程学院，益阳 413000)

1 引 言

钱令希[1]指出力学性能约束可划分为局部性约束和整体性约束，这是就截面层次优化的划分，同样也适用结构拓扑优化层次[2-5]。

力学性能局部性与整体性的区别直接影响建模与求解的差别。局部性力学性能约束下的结构优化问题中，出现了建模困难。因约束太多，其个数是单元或子域的个数与载荷工况的乘积。不管应力和局部稳定还是疲劳寿命约束，相关性能在每个单元或子域上都必须满足。而整体性力学性能约束，如位移或频率约束，约束数目相比局部性能约束少很多，相应的敏度计算量也因为各种处理如采用伴随法而变得比局部性能约束少很多。

局部性能与整体性能的本质区别在于单元对于性能的作用不同，局部性约束要求在所有单元里相关的性能都不能违背，故称为单元满足型；整体性约束只要求结构总体不能违背相关的性能，故称为性能的单元贡献型。为了克服局部性能约束优化问题的困难，以往研究已提出过分部[1,2-5]、化整[3-5]及集成[2,3,9-13]3种解法，分别简称为P解法(Partition approach)、G解法(Globalization approach)和I解法(Integration approach)。本文将阐述与之相关新提出的3种交融(Blending)即B解法,分部-集成(Partition-Integration approach)即 P -I 解法、化整-集成(Globalization-Integration approach)即G -I解法以及集成-集成(Integration-Integration approach) 即I -I解法。

2 局部性能约束优化问题四种解法的演化

2.1 P解法

在Schmit[6]奠定结构优化成为独立学科基础之前，结构设计的满应力准则其实就是分部优化解法。Shanley等[7,8]提出的同步失效准则，为解决航空结构受压构件设计需要确定每个截面一组尺寸集，本质上还是分部优化解法。文献[1]除了叙述桁架满应力设计，还叙述了钢框架和钢筋混凝土框架的构件优化设计，也归于分部优化解法。分部优化解法的前提是在超静定结构中引进内力暂时不变的处理，或者说引入了每轮设计中结构静定化假设。文献[2-5]在连续体结构拓扑优化的一系列研究中，也沿用了结构静定化假设。

2.2 G解法

能否在建模时把各单元的相互关联和影响考虑进去？该想法导致产生了应力全局化方法，即化整优化方法[3-5]。

2.3 I解法

Yang等[9]最先提出了用K-S函数将众多应力约束集成为一个，进行结构拓扑优化设计。文献[10,11]也采用凝聚函数包括K-S函数集成应力约束的结构拓扑优化研究，并作了详细阐述[2,3]。Paris等[12]及Luo等[13]先后引用K-S函数将结构拓扑优化应力约束集成化。将众多约束化为一个，是化整优化方法和集成优化方法的共性，但是前者借助于力学原理，后者则借助于数学公式。

2.4 B解法

B解法是新提出的交融优化方法，细分为3种(P -I，G -I和I -I)解法，皆植根于互逆规划的定理2[14,15]。3种交融优化方法在每一次迭代求解中，都包括单目标方和多目标方两部分，交替求解局部性约束的优化模型，较之局部性约束的P，G和I解法，3种B解法分别提高了求解效率。

3 疲劳性能的分部特点和化整变换

3.1 疲劳性能约束同应力约束的类比

疲劳约束如同应力约束，都属于单元性能满足型约束，相应的结构优化模型表示为

(1)

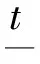
若是静定结构，其内力不随设计变量变化而改变，同应力约束问题类似，可求解N个单元疲劳寿命子问题，求解后Li l(ti)不变，一次就求得结果。连续体属于超静定结构，不可能像静定结构那样结构分析一次就得到最优解，但是可以借助静定化假设，迭代逼近式(1)的整体最优解。仿满应力准则，可以称此为满疲劳设计准则。

3.2 从单元疲劳寿命化整出结构疲劳寿命

既然应力约束优化可借助应变能化整为全局约束，那么对于疲劳约束，也能做类似的工作。为此，考虑循环载荷下的应力寿命S -N曲线，按巴士昆(Basquin)公式，有

σ=AL- m

(2)

式中σ为疲劳循环下受拉实验杆的材料极限应力，L为对应的疲劳寿命，A与m为材料给定的相关量，皆为正数。

由式(2)可推得能量的表达式为

(3)

式中e为实验杆的应变能，v为杆的体积，E为杨氏模量。

把式(3)推广到单元复杂应力状态下的疲劳问题，可以得到

(4)

为了推导出疲劳约束全局化的公式，须把式(4)用于结构疲劳问题的单元上，稍加整理，然后求和可以得到结构疲劳寿命的表达式为

(5)

式中ei l与Li l分别为l工况下i单元的单元应变能与单元疲劳寿命，vi为i单元体积。右边表示l工况下i单元的寿命之和，故可以称为疲劳载荷l工况下的结构寿命。

3.3 疲劳过滤函数及其在疲劳约束显式化中的作用

沿袭以往的研究，基于ICM方法，利用不同的过滤函数，将结构拓扑优化模型近似显式化。为此，类比对应力约束的处理措施[3-5]，给出疲劳约束对应的有关公式。

在应力约束的拓扑优化中，涉及到P解法、G解法和I解法，当中相应的过滤函数有不同的选择。

P解法的应力约束若取应力为约束[3,4]，有

(6)

P解法的疲劳约束，类比应力约束式(6)得

(7)

若取应变能表示P解法的应力约束，单元应力约束和全局化的结构应力约束可表示为

(8a)

(8b)

式(8a)左端为结构应变能，其单元应变能为

(9)

式中σi l，εi l与Pi l为l载荷工况下i单元的应力、应变与节点力向量，Ki与Ωi分别为i单元的刚度矩阵及子域。

(10)

(11)

(12)

至此，将式(12)代入式(5)的第i项得

(13)

于是，得到G解法疲劳性能化整之后全局化的结构寿命约束为

(14)

3.4 疲劳约束与应力约束的统一规格

为了疲劳约束优化问题的求解与应力约束优化问题的求解一致，引入了倒寿命的概念，

I=1/L

(15)

在倒寿命概念下，由式(7，13，14)得

(16a)

(16b)

将式(12)代入式(8)得

(17a)

(17b)

式(16,17)表明疲劳与应力统一了约束规格。

顺便归纳一下过滤函数的取法,(1) 应力约束时，P解法和I解法皆按式(6,17a)取；G解法按 式(17b)取。(2) 疲劳约束时，P解法和I解法按 式(16a)取；G解法按式 (16b)取。

4 局部性能约束单目标模型三种解法

本节补充和完整了已有的局部性能约束解法，属于单目标模型分别为分部、化整和集成解法三种，下面分别用P模型、G模型和I模型表示。

4.1 P解法(Partition approach)

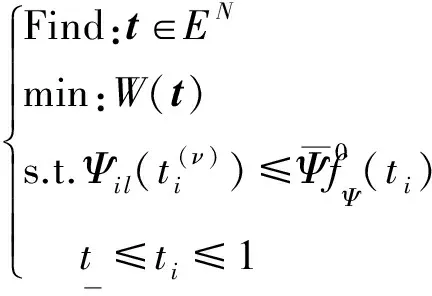
(18)

式中性能符号Ψ为应力或疲劳寿命，当为应力时，按式(6)或式(17a)取；当为疲劳寿命时，按式(16a)取。依静定化假设求得

(19)

式(19)尚需按变量的上下限予以修正。

4.2 G解法(Globalization approach)

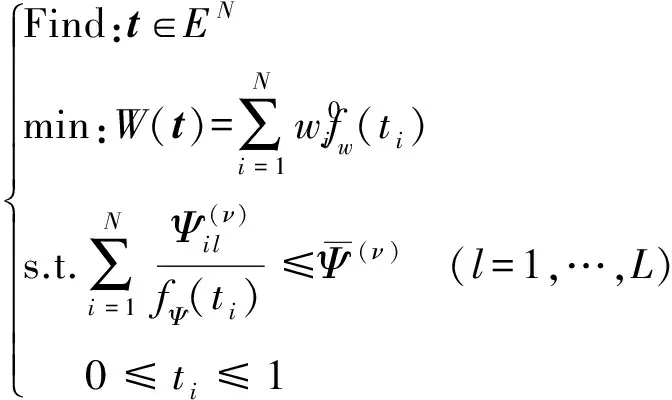
(20)

其中性能符号Ψ分别由式(17b)或式(16b)取得。可采用DSQP或DP -EM方法[16]求解。

4.3 I解法(Integration approach)

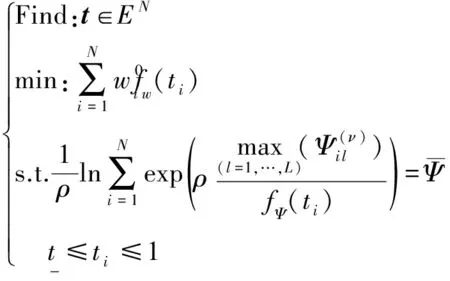
(21)

(22)

(23)

接着，将式(21)转化到x空间里，通过目标二阶近似，用Lagrange乘子法求得显式解，迭代逼近，得

(24)

回代到t空间里得式(21)的解。篇幅所限，详细推导过程从略。

5 局部性能约束的单目标与多目标模型交替迭代的三种交融解法

5.1 三种交融解法

本节突破和开拓出了局部性能约束的新解法，属于单目标与多目标模型交替迭代的交融解法，共三种：(1) P -I 解法(Partition-Integration approach)； (2) G -I 解法(Globalization-Integration approach)； (3) I -I 解法(Integration-Integration approach)。

标识三种解法的前一个字母，代表第4节的三种单目标模型；后一个字母，代表第5.3节即将介绍的多目标的集成模型，唯有一种。

5.2 交融解法的迭代寻优算法

(1) 迭代次数赋初值ν=1。

(2) 实施模块1,即进行结构分析。

(3) 实施模块2,建立4.1～4.3三种模型之一，求解得最优重量W*。

(6) 结束迭代。

5.3 交融解法中的多目标集成模型

多目标模型集成模型可写为

(25)

式中目标函数的含义与第4.1节P模型的约束相同，此处不再赘述。用Lagrange乘子法推导出规划(25)的显式解，

(26)

迭代求解中，当t(v + 1)与t(v )充分接近后收敛，每次小循环迭代都用0≤ti≤1修改迭代解。限于篇幅，具体推导从略。

6 数值算例

6.1 MBB梁的应力约束拓扑优化

基结构是宽为300 mm、高为50 mm简支梁，集中载荷F=200 N作用于跨中顶点，因对称性取一半结构和一半载荷进行计算，计算简图和支座约束如图1所示，采用150×50网格。弹性模量E= 2.1×105MPa，泊松比为0.3。为避免应力集中，F分散作用在相邻的4个结点上，右下角竖向约束也分散在2个结点上。许用应力[σ]=100 MPa。

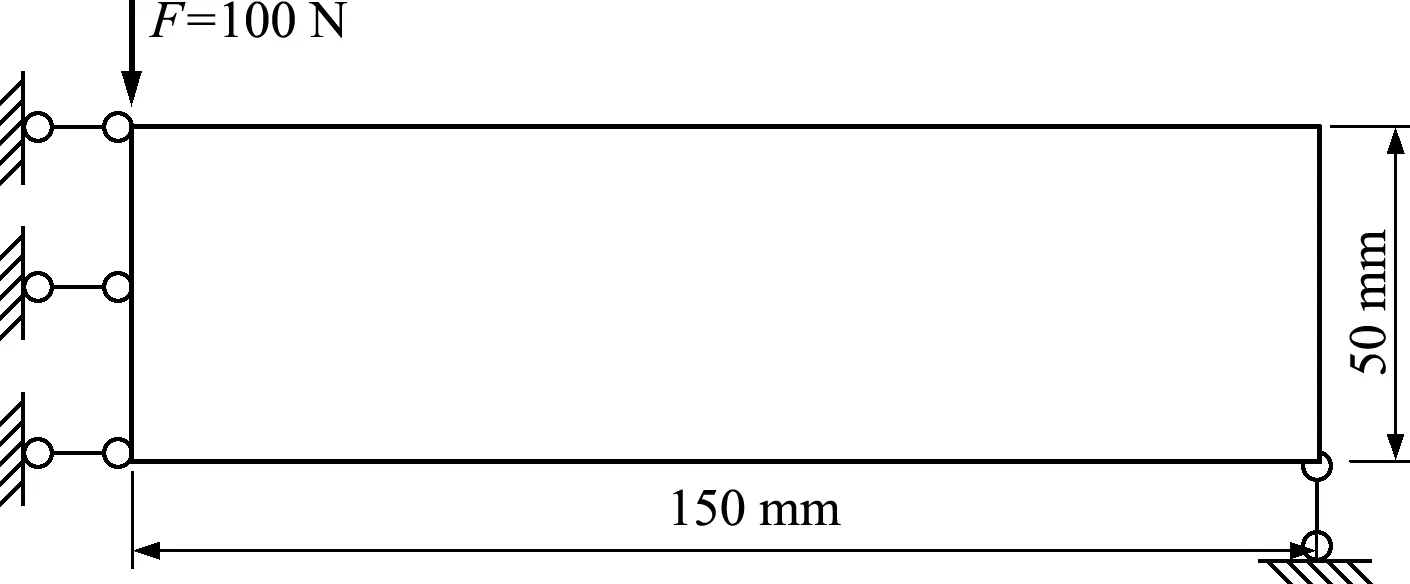
图1 MBB梁问题取一半结构的分析及优化模型

本算例分别以单纯集成方法(I解法)及集成-集成交融方法(I -I 解法)求解应力约束体积极小化问题。I解法经过61次迭代收敛，最优体积比为 0.548，最大Mises应力为100.373 MPa。I -I 解法经过47次迭代收敛，最优体积比为0.553，最大Mises应力为99.900 MPa。两种方法得到的最优拓扑如图2所示，对应的Mises应力分布如图3所示，目标及约束的迭代历史曲线对比如图4所示。相比I解法，I -I解法的迭代次数减少了14次，收敛更快。

图2 单纯集成方法与集成-集成交融方法得到的最优拓扑

图3 单纯集成方法与集成-集成交融方法的最优时Mises应力分布

图4 集成方法与集成-集成交融方法优化过程目标及约束对比

6.2 两端固支梁的应力约束拓扑优化

如图5所示，基结构尺寸为120 mm×60 mm×1 mm的平面体，采用200×100网格。材料弹性模量为E=2.1×105MPa，泊松比ν=0.3。左右边界固定。工况1,集中载荷F1=300 N作用于上边界中点；工况2, 集中载荷F2=300 N作用于下边界中点。划分为200×100个矩形单元。应力约束为100 MPa。

图5 两工况算例分析及优化的模型

I解法经过64次迭代收敛，最优体积比为 0.170，最大Mises应力为102.590 MPa。I -I 解法经过57次迭代收敛，最优体积比为0.142，最大Mises应力为96.58 MPa。两种方法得到的最优拓扑如图6所示，对应的两个工况下的Mises应力分布如图7和图8所示，目标及约束的迭代历史曲线对比如图9所示。经对比可以看出，两种方法得到的最优拓扑构型不仅相似，对应的Mises应力也是相似的。I -I 解法得到的最优体积比略小。相比I解法，I -I 解法的迭代次数减少了7次，收敛 更快。

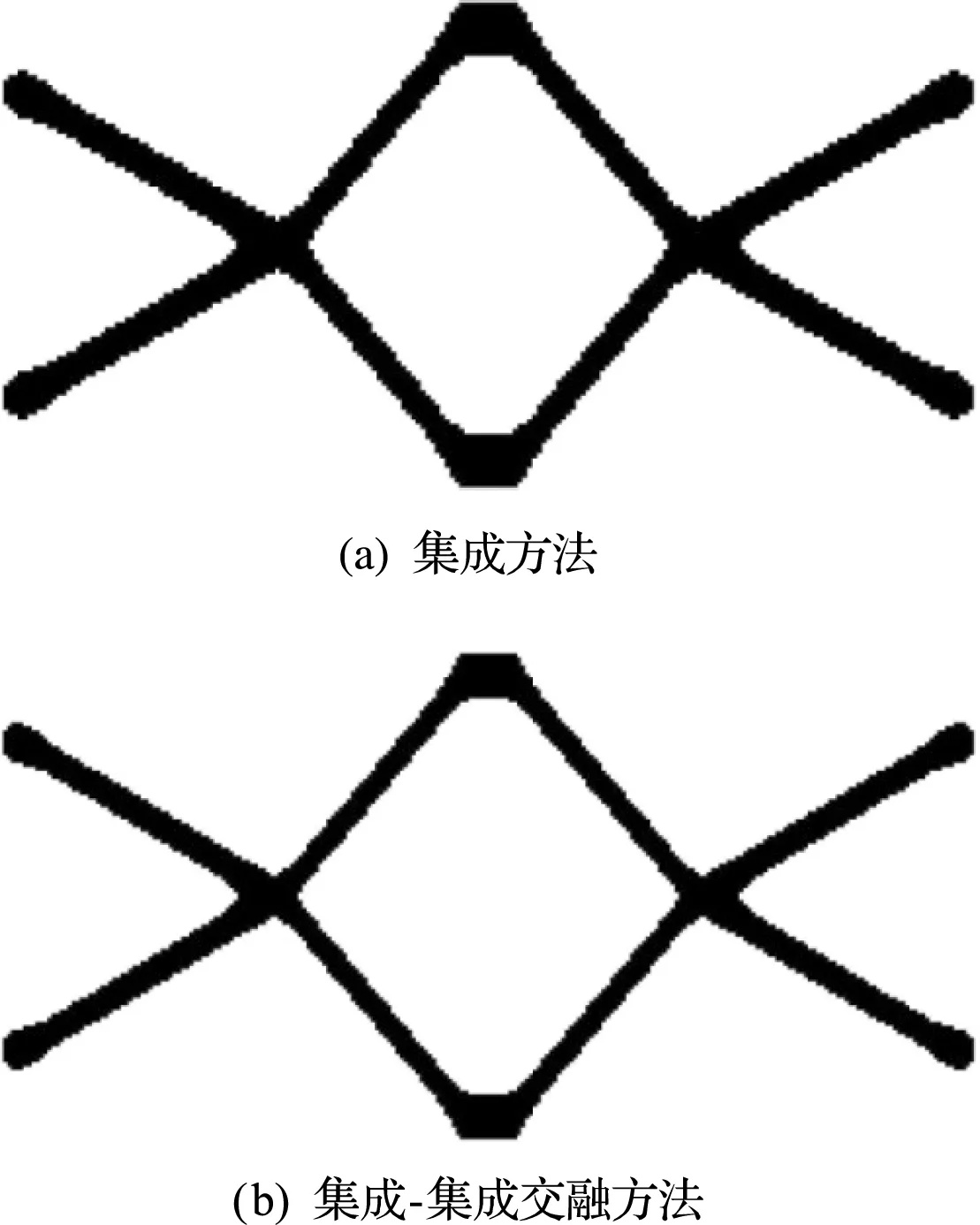
图6 集成方法与集成-集成交融方法得到的最优拓扑

图7 集成方法与集成-集成交融方法的最优时工况1的Mises应力分布

图8 集成方法与集成-集成交融方法的最优时工况2的Mises应力分布

图9 集成方法与集成-集成交融方法优化过程目标及约束对比

6.3 五次超静定梁的疲劳约束拓扑优化

如图10所示，材料性能为E=2.1×105MPa，泊松比ν=0.3，材料对应于循环次数1.0×106的疲劳极限为σs=250 MPa，基结构为 800 mm×200 mm×10 mm的平面体，划分为400×100个矩形单元。基结构的四个角点皆为双向约束铰支座。工况为正弦形式循环载荷F=21000 N且均值为0，相位角为0，作用于图10基结构的中心点，为了避免应力集中将荷载施加在五个节点上。疲劳寿命约束为大于或等于1.0×105次。Basquin公式中常数值取m=0.10，A=995.3 MPa。

图10 五次超静定梁结构的优化模型

Fig.10 Model of structure for analysis and optimization of the statically indeterminate beam

本算例分别以单纯分部方法(P解法)及分部-集成交融方法(P -I 解法)求解疲劳寿命约束体积极小化问题。P解法经过36次迭代收敛，最优体积比为0.488，最大疲劳寿命为99141次。P -I 解法经过26次迭代收敛，最优体积比为0.483，最大疲劳寿命为100675次。两种方法得到的最优拓扑如 图11 所示，对应的疲劳寿命以10为底的对数分布如图12所示，目标及约束的迭代历史曲线对比如 图13 所示。相比P解法，P -I 解法的迭代次数减少了10次，收敛更快。

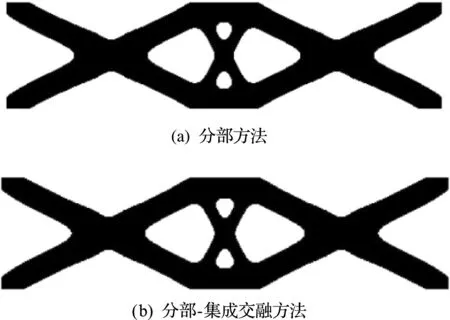
图11 单纯分部方法与分部-集成交融方法得到的最优拓扑

图12 分部方法与分部-集成交融方法的最优时疲劳寿命分布

图13 分部方法与分部-集成交融方法优化过程目标及约束对比

7 结 论

类比对应力约束的处理措施，给出疲劳约束对应的过滤函数。仿应力约束问题的满应力准则，介绍了满疲劳设计准则。仿应力约束问题的化整方法的全局化应力约束，给出了疲劳约束化整方法的全局化疲劳约束。基于倒寿命的概念，实现了疲劳约束与应力约束的规格统一。对结构疲劳约束与应力约束的局部性能约束问题，梳理了3种单目标优化方法，阐述了新提出的由单目标与多目标交替迭代的3种交融优化方法。数值算例表明，交融解法的求解效率，比单目标解法更加有效，这是每次结构分析之后做了两次寻优的必然结果。

致谢:硕士生张译文同学参加了算例计算。

参考文献(References):

[1] 钱令希.工程结构优化设计[M].北京：水利电力出版社,1983.(QIAN Ling-xi.OptimizationDesignforEngineeringStructures[M].Beijing:Water Conservancy and Electric Power Press,1983.(in Chinese))

[2] 隋允康.建模·变换·优化:结构综合方法新进展[M].大连：大连理工大学出版社,1996.(SUI Yun-kang.ModelingTransformaionandOptimzation:NewDevelopmentofStructuralSsynthesisMethod[M].Dalian:Dalian University of Technology Press,1996.(in Chinese))

[3] 隋允康,叶红玲.连续体结构拓扑优化的ICM方法[M].北京:科学出版社,2013.(SUI Yun-kang,YE Hong-ling.ContinuumTopologyOptimizationICMMethod[M].Beijing:Science Press,2013.(in Chinese))

[4] Sui Y K,Peng X R.Modeling,SolvingandApplicationforTopologyOptimizationofContinuumStructures,ICMMethodBasedonStepFunction[M].Elsevier,2018.

[5] 隋允康，叶红玲，彭细荣.应力约束全局化策略下的连续体结构拓扑优化[J].力学学报，2006,38(3):364-370.(SUI Yun-kang,YE Hong-ling,PENG Xi-rong.Topologicaal optimization of continuum structure under the strategy of globalization of stress constraints [J].ChineseJournalofTheoreticalandAppliedMechanics,2006,38(3):364-370.(in Chinese))

[6] Schmit L A.Structural design by systematic synthesis[A].Proceeding of Conference on Electronic Computation,ASCE[C].New York， 1960.

[7] Shanley F R.Weight-StrengthAnalysisofAircraftStructures[M].New York,1960.

[8] Spunt L.OptimumStructuralDesign[M].New Jersey,1971.

[9] Yang R J,Chen C J.Stress -based topology optimization[J].StructuralOptimization,1996,12(2):98-105.

[10] 隋允康，张学胜，龙连春.应力约束处理为应变能集成的连续体结构拓扑优化[J].计算力学学报,2007,24(5):602-608.(SUI Yun-kang,ZHANG Xue -sheng,LONG Lian-chun.ICM method of the topology optimization for continuum structures with stress constraints approached by the integration of strain energies[J].ChineseJournalofComputationalMecha-nics，2007,24(5):602-608.(in Chinese))

[11] 隋允康，铁 军.结构拓扑优化ICM显式化与抛物型凝聚函数对于应力约束的集成化[J].工程力学，2010,27(2):124-133.(SUI Yun-kang,TIE Jun.The ICM explicitation approach to the structural topology optimization and the integrating approach to stress constraints based on the parabolic aggregation function [J].EngineeringMechanics,2010,27(s2):124-133.(in Chinese))

[12] París J,Navarrina F,Colominas I,et al.Improvements in the treatment of stress constraints in structural topology optimization problems [J].JournalofComputationalandAppliedMathematics,2010,234(7):2231-2238.

[13] Luo Y J,Wang M,Kang Z.An enhanced aggregation method for topology optimization with local stress constraints[J].ComputerMethodsinAppliedMechanicsandEngineering,2013,254(2):31-41.

[14] 隋允康，彭细荣，叶红玲，等.互逆规划理论及其用于建立结构拓扑优化的合理模型[J].力学学报，2019,51(6):1-9.(SUI Yun-kang，PENG Xi-rong，YE Hong-ling，et al.Reciprocal programming theory and its application to establish a reasonable model of structural topology optimization[J].ChineseJournalofTheoreticalandAppliedMechanics,2019,51(6):1940-1948.(in Chinese))

[15] 铁 军,隋允康,彭细荣.互逆规划的拓宽和深化及其在结构拓扑优化的应用.力学学报,2020,52(6):1822-1837.(TIE Jun,SUI Yun-kang,PENG Xi-rong.Widening and deepening of reciprocal programming and its application to structural topology optimization[J].ChineseJournalofTheoreticalandAppliedMe-chanics，2020，52(6)：1822-1837.(in Chinese))

[16] Sui Y K,Peng X R.Explicit model of dual programming and solving method for a class of separable convex programming problems[J].EngineeringOptimization,2019,51(9):1604-1625.