针对注塑成型随形冷却的流热力耦合拓扑优化方法研究

(1.大连理工大学 工业装备结构分析国家重点实验室，大连 116024；2.郑州大学 橡塑模具国家工程研究中心，郑州 450002)

1 引 言

塑料制品广泛应用于汽车、建筑、机械和农业等领域，是我国经济发展支柱性产业之一。随着材料技术的发展，研发出各种工程塑料和特种塑料，为信息电子和航空航天等高科技产业的发展提供制造可能。与此同时，对塑料制品的性能、制造精度和外观都有了更高要求。注塑成型作为塑料加工的主要方法之一，因其生产精度高、便于制造形状复杂的产品以及可批量生产等特点，占据了当前塑料工业生产的重要位置。注塑过程中，高温熔体传入模具的热量95%以上经由散热管道内的冷却剂带出模具，其余部分以对流和辐射方式从模具外表面传出[1]。模具冷却作为注塑成型的关键环节[2]，其型腔的冷却速度和均匀性影响着塑料制品的生产效率以及产品质量，因此如何使模具更快和更均匀地散热成为当前注塑成型工艺的一个重点问题[3]。

传统的工艺设计方法主要依赖于试模，但开模成本较高，为满足高质量塑料制品的生产需求，许多学者基于数值模拟技术对注塑成型模具冷却系统进行参数优化设计。Tang等[4]采用伽辽金有限元法的无矩阵雅可比共轭梯度形式模拟瞬态热传导，对冷却管道的尺寸、位置和冷却剂流量进行设计。Dang等[5]以汽车塑料挡泥板为例，将铣削加工中U形铣槽冷却管道的直径、间距和深度作为设计变量，借助三维CAE仿真工具，结合DOE试验设计方法建立响应面模型，对冷却管道进行优化。Li等[6]在注塑模具冷却系统布局阶段，考虑不干扰其他模具部件的情况下，在模具镶件处建立冷却系统，提出配置空间(C-space)的概念，结合遗传算法进行冷却系统布局可行设计搜索。

还有一些学者基于直观感受或工程经验，引入启发式方法进行散热管道设计。Peng等[7]以植物叶片的脉络结构为基础，设计了带有渗透壁和多孔介质的分支网络散热装置。Barber等[8]受到动物血管的仿生学原理启发，对矩形、梯形截面通道微流控系统进行研究。对于三维的复杂结构散热问题，Au等[9]用多面体形状近似模具表面，并根据照明原理在设计空间内找出能够照亮多面体形状的若干光源点，再通过连接光源点进行冷却通道设计，使模具表面达到均匀冷却目的。上述参数优化工作都是针对传统的平行管道进行设计，虽然较于原始设计有明显的改进效果，但其优化结构依赖于经验给出的初始管道结构，具有较强的局限性。与参数优化相比，启发式方法可获得优于传统管道设计方法的结果，且计算效率高，但其并未对模具冷却过程进行数值模拟分析，无法确定是否获得最优解。

相比参数优化的局限性以及启发式方法的精确性不足，拓扑优化结合数值模拟技术进行材料分布优化具有较高的计算可靠性和设计自由性。近年来，许多学者将结构拓扑优化方法引入流热耦合领域中解决散热器优化设计问题。Dede等[10]对微流控分析芯片进行多通道拓扑的单相流微通道冷却板研究。Ya等[11]基于二维和三维稳态N-S(Navier-Stokes)方程及能量方程，将散热结构设计表述为一个热交换最大化问题，采用水平集法对管道边界进行描述。Tawk等[12]建立bi-eta插值函数以及流动连续性函数，将密度法用于包含两种流体和一种固体的多相热交换器的结构设计中，实现了二维的双流体传热传质结构拓扑优化。Zheng等[13]基于周期平均法和边界元研究了注塑成型随形冷却管道拓扑优化设计。该方法首先基于随形面给定初始管网分布，并将管道节点坐标和半径作为优化变量，最终得到复杂的三维管道。该工作采用了工程计算模型来分析管道流速，虽然可以大幅度提高计算效率，但是对于曲率很大的管道网络，计算精度无法保证。

本文以伪密度作为设计变量，对流固材料进行插值描述，采用移动渐近线法求解拓扑优化问题，结合连续伴随法进行灵敏度分析，对注塑成型模具冷却管道的拓扑优化设计展开研究。本文还对比了是否考虑模具结构承载力的拓扑优化结果，发现不考虑结构承载力的冷却管道优化设计不具备工程应用意义，而将结构柔度作为约束条件之一，可以较好地解决实际加工中考虑模具承载能力影响的冷却管道设计问题。

2 控制方程

2.1 流动控制方程

在注塑成型模具的冷却管道设计中，冷却剂常视为粘性不可压缩定常流。一般情况下湍流状态冷却介质的散热能力优于层流，但基于密度法的湍流拓扑优化由于无法识别流固边界，目前仍存在诸多问题，如无法设置壁面函数、无法对边界层网格加密和难以准确计算近壁距离等。故本文选择定常层流N-S方程作为流动控制方程。

连续性方程

·u=0

(1)

动量守恒方程

(2)

在大多数基于变密度法的流体拓扑优化工作中，通常以达西渗流理论作为控制方程出发点，即增加多孔介质流阻力项f=-αfu来表征流固材料分布情况。因此动量守恒方程可表示为

(3)

式中αf为材料流阻系数，其通过式(3)进行材料密度插值[14]。

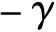
(3)

2.2 传热控制方程

注塑成型是一个周期性循环过程，这决定了型腔面温度也随时间进行变化。注塑过程进入周期稳态后，模具表面瞬时温度虽然会变化，但其平均温度不变。在实际的模具冷却分析应用中，一般利用周期平均温度代替瞬时温度，将原瞬态问题转化为稳态问题[1]。故注塑成型问题的传热控制方程可表示为

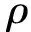
(5)

(6)

(7)

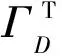
热传导系数插值

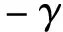
(8)

式中qk为正常数，本文取0.01；kf为流体热传导系数；ks为固体热传导系数。

2.3 结构平衡方程

当塑料熔体以高压注入模具时，注塑机的锁模元件要对模具施加足够的锁模力克服型腔内熔体的胀模力。由于冷却管道会影响模具的刚度，为保证模具在巨大的锁模力下不受损坏，则应在散热系统优化设计时考虑结构承载力。本文基于模具结构承载力因素进行算例对比研究，线弹性力学平衡方程可表示为

(9)

(10)

(11)

(12,13)

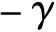
(14)

式中qE为正常数，本文取0.01；Emin为孔洞的杨氏模量，Emax为固体材料的杨氏模量，为避免计算过程中出现矩阵奇异，取Emin=10-9Emax。

2.4 拓扑优化列式

散热性能是冷却系统的主要关心指标，本文以平均温度为目标函数衡量其散热效果,

(15)

式中Ψ表示目标函数，|Ω|为计算域总体积。

冷却系统的散热能力与流场的能量耗散有关，一般情况下，流场压力降越大则散热效果越好。但在工程应用中其受到冷水机功率限制，故本文对流场的能量耗散进行约束。

(16)

式中Γin,out为冷却管道的出入口边界。

根据2.3节对结构平衡方程的介绍可知，注塑过程中要保证模具能承受住锁模力，因此本文以结构柔度作为约束函数之一,

(17)

综上所述，基于变密度法的流-热-力耦合拓扑优化问题的数学列式可表示为

MinimizeΨ

(18)

2.5 过滤方法

基于变密度法的拓扑优化会出现棋盘格效应以及产生灰度单元等问题。为了解决上述问题，本文联合使用Helmholtz偏微分方程[15]和双曲正切投影[16]进行密度过滤。

Helmholtz偏微分方程表达式为

(19)

双曲正切投影表达式为

(20)

3 拓扑优化数值实现

3.1 优化方法

拓扑优化问题的目标函数及约束函数一般为设计变量的隐式表达，且拓扑优化问题通常具有非凸性和高非线性，计算量大。当前求解拓扑优化问题的主要方法分为优化准则法和序列规划法两类。在序列规划法中，移动渐近线法MMA(method of movingasymptotes)[17]的变量独立且只需求解一阶导数就能达到很好的收敛效果，故本文采用此方法进行求解。

3.2 灵敏度分析

由于拓扑优化中设计变量个数远大于目标和约束函数个数，因此一般采用伴随法敏度分析一次计算出目标函数(或约束)对所有设计变量的导数。伴随法又可分为连续伴随法和离散伴随法两种，其区别在于对控制方程进行离散和求导的先后次序。离散伴随法需要用到雅克比矩阵以及雅克比矩阵对设计变量的导数。如果控制方程采用分离式求解算法(如求解N-S方程的SIMPLE[18]算法)，则雅克比矩阵在计算过程中并未组集，这给伴随敏度分析带来困难。本文采用连续伴随法计算灵敏度，其出发点为将连续的状态方程与伴随变量相乘并增广到目标函数上，通过对拉格朗日函数求加托导数以及分部积分，最终得到连续形式的伴随方程与伴随边界条件。该方法优点在于伴随方程和状态方程相互独立，可以选择对伴随方程使用耦合或分离式求解器。该优点和支持自定义PDE求解器的CAE软件结合时，可以极大地减少用户在敏度分析方面的编程操作。

拉格朗日函数

(21)

(22)

式中Ψ为目标函数，此处引入如式(22)所示一般化积分形式进行表述。θ为拉格朗日乘子，R为控制方程。对于本文来说，R即为N-S方程、能量守恒方程及结构平衡方程。θ=(ua,pa,Ta)为伴随变量。

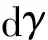
(23)

根据偏微分方程约束最优化问题的KKT条件有

(24)

则设计变量灵敏度可求解得

(25)

从式(22,23)可推得伴随Navier-Stokes方程为

∂A/∂p=·uainΩ

(26)

inΩ

(27)

(28)

-∂A/(∂uT)·n-∂B/∂u(u·n)ua+

(29)

伴随能量守恒方程

inΩ(30)

(31)

-∂A/(∂T)·n-∂B/∂T=cTau+kTa]·n

式中ua和Ta分别为伴随速度场和伴随温度场，式(24～30)的左端项列入表1。

表1 伴随方程左端项

由于最小化结构柔度的线弹性力学问题是自伴随的，即伴随变量等于结构位移，此处省略该问题的伴随敏度分析。

3.3 基于OpenFOAM进行优化问题求解

本文基于OpenFOAM[19]搭建拓扑优化求解器。流-热-力耦合拓扑优化流程如图1所示，首先读取材料参数，再对Navier-Stokes方程以及结构平衡方程进行计算，得到速度场和位移场之后，将速度场带入能量守恒方程求得温度场。完成以上初始场计算后，对伴随控制方程进行求解，得到各伴随变量，然后计算目标函数以及约束函数对设计变量的灵敏度。最后调用MMA更新设计变量。

图1 基于OpenFOAM拓扑优化求解流程

4 算 例

本文采用的注塑成型初始模具的几何形状与尺寸如图2所示，尺寸单位为毫米(mm)。

图2 对称结构尺寸

4.1 不考虑结构承载的流-热耦合拓扑优化

4.1.1 算例参数

本文算例的模具冷却管道不可设计域如图3所示，分别为模具冷却管道的出入口部分以及模具型腔面。为减少拓扑优化过程中的计算量，对模型施加对称边界条件。冷却管道入口处法向速度为 0.01 m/s，温度为0，冷却管道出口处为绝热边界。热源面施加均布压力10 MPa和热流量40000 W/m2，其他边界面为绝热无滑移面。本算例选用的材料参数列入表2。

图3 模具不可设计域

图4 模具工况

表2 材料参数

4.1.2 传统冷却管道设计

在注塑成型模具中，传统的冷却管道通常为直管设计，本文将传统直管设计作为拓扑优化初始构型进行模具冷却仿真模拟。初始直管设计的流体材料用量百分比为1.4%，模具平均温度为83.5 ℃，能量耗散为6.861×10-10kg·m2/s3，结构柔度为 0.086 J。因此，在本文优化算例中，给定流体材料百分比上限为3%，能量耗散为直管模型的2倍，结构柔度为直管模型的1.5倍。

图5 传统直管冷却温度场

4.1.3 优化结果

本算例不考虑模具结构承载能力进行拓扑优化，其优化列式为

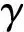
MinimizeΨ

(33)

优化后管道设计如图6所示。优化后的管道构型与模具型腔紧密贴合，结构整体刚度不足，在注塑过程中模具易损坏，且不具备模具实际制造条件，故下文将考虑模具结构承载力重新进行冷却管道优化设计。

图6 不考虑模具承载能力优化结果

4.2 考虑结构承载的流-热-力耦合拓扑优化

在4.1节的优化模型基础上增加考虑结构承载力的结构柔度约束进行优化设计，优化列式如式(18)所示。

本算例冷却管道拓扑优化构型如图7所示，冷却管道沿着模具型腔面均匀覆盖。结构温度场如图8所示，结构最高温度出现在模具型腔面临近出口边缘处，优化结果显示此处形成了流道以带走模具热量。拓扑优化后的模具平均温度为76.0 ℃，与传统直管设计相比，拓扑优化后的冷却管道设计使模具的平均温度降低了9%。

图7 考虑结构承载能力的拓扑优化管道构型

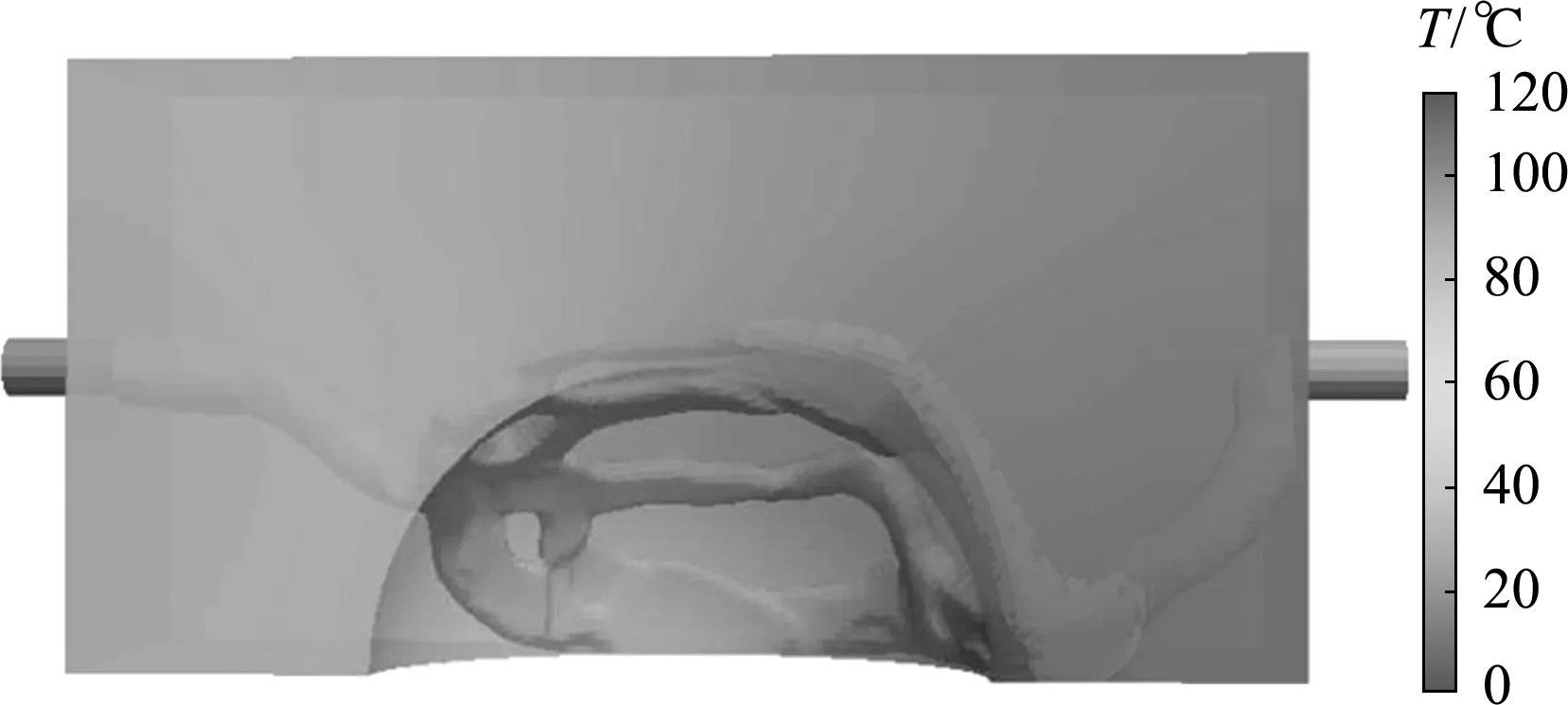
图8 考虑结构承载能力优化后温度场

5 结 论

本文基于变密度法进行注塑模具冷却管道拓扑优化设计，采用插值函数描述流固材料分布，以最小结构平均温度为设计目标。联合使用Helmholtz偏微分方程和双曲正切投影方程进行密度过滤，得到了清晰的冷却管道拓扑形态。通过对比是否考虑模具承载能力的两个算例，得出注塑成型中应该将模具承载性能作为评价指标的结论。最后基于OpenFOAM平台对注塑成型冷却系统设计问题进行三维流-热-力耦合拓扑优化，得到了冷却效果良好且具有实际加工意义的流体通道设计。与传统的直管冷却系统相比，拓扑优化后的冷却系统能够使模具平均温度降低9%。

本文仅是对于注塑成型冷却系统设计的初步研究，目前还存在诸多不足,如应采用周期平均法计算模具型腔面处的平均压力和热源值当做优化的边界条件；应该采用湍流模型模拟冷却介质的流动传热性能。未来将从以上角度对优化进行改进。

参考文献(References):

[1] 石宪章.注塑冷却数值分析方法的研究与应用[D].郑州大学,2005.(SHI Xian-zhang.Study and Application of Numerical Method for Cooling Analysis in Injection Molding[D].Zhengzhou University,2005.(in Chinese))

[2] 申长雨,李海梅,高 峰.注射成型技术发展概况[J].工程塑料应用,2003，31(3):53-57.(SHEN Chang-yu,LI Hai-mei,GAO Feng.Development survey of injection molding[J].EngineeringPlasticsApplication,2003，31(3):53-57.(in Chinese))

[3] 王 勇.基于快速随形热冷的高光无痕注塑成型[D].湖北工业大学,2018.(WANG Yong.High Gloss Seamless Injection Molding Based on Rapid Shape Following Thermalcool[D].Hubei University of Technology,2018.(in Chinese))

[4] Tang L Q,Chassapis C,Manoochehri S.Optimal cooling system design for multi-cavity injection molding [J].FiniteElementsinAnalysisandDe-sign,1997,26(3):229-251.

[5] Dang X P,Park H S.Design of U-shape milled groove conformal cooling channels for plastic injection mold[J].InternationalJournalofPrecisionEngineeringandManufacturing,2011,12(1):73-84.

[6] Li C G,Li C L.Plastic injection mould cooling system design by the configuration space method[J].Computer-AidedDesign,2008,40(3):334-349.

[7] Peng Y,Liu W Y,Chen W,et al.A conceptual structure for heat transfer imitating the transporting pri-nciple of plant leaf[J].InternationalJournalofHeatandMassTransfer,2014,71:79-90.

[8] Barber R W,Emerson D R.Optimal design of microfluidic networks using biologically inspired principles[J].MicrofluidicsandNanofluidics,2008,4(3): 179-191.

[9] Au K M,Yu K M,Chiu W K.Visibility-based conformal cooling channel generation for rapid tooling[J].Computer-AidedDesign,2011,43(4):356-373.

[10] Dede E M.Optimization and design of a multipass branching microchannel heat sink for electronics cooling[J].JournalofElectronicPackaging,2012,134(4):041001.

[11] Yaji K,Yamada T,Kubo S,et al.A topology optimization method for a coupled thermal-fluid problem using level set boundary expressions[J].Interna-tionalJournalofHeatandMassTransfer,2015,81:878-888.

[12] Tawk R,Ghannam B,Nemer M.Topology optimization of heat and mass transfer problems in two fluids — one solid domains[J].NumericalHeatTransfer,PartB:Fundamentals,2019,76(3):130-151.

[13] Li Z,Wang X Y,Gu J F,et al.Topology optimization for the design of conformal cooling system in thin-wall injection molding based on BEM[J].TheInternationalJournalofAdvancedManufacturingTechnology,2018,94(1-4):1041-1059.

[14] Borrvall T,Petersson J.Topology optimization of fluids in Stokes flow[J].InternationalJournalforNumericalMethodsinFluids,2003,41(1):77-107.

[15] Lazarov B S,Sigmund O.Filters in topology optimization based on Helmholtz-type differential equations[J].InternationalJournalforNumericalMethodsinEngineering,2011,86(6):765-781.

[16] Wang F W,Lazarov B S,Sigmund O.On projection methods,convergence and robust formulations in topology optimization[J].StructuralandMultidisciplinaryOptimization,2011,43(6):767-784.

[17] Svanberg K.The method of moving asymptotes—a new method for structural optimization[J].InternationalJournalforNumericalMethodsinEnginee-ring,1987,24(2):359-373.

[18] Patankar S V,Spalding D B.A calculation procedure for heat,mass and momentum transfer in three -dimensional parabolic flows[J].InternationalJournalofHeatandMassTransfer,1972,15(10):1787-1806.

[19] Open FOAM.AC++LibraryforComplexPhysicsSimulations[M].2007.