对一堂优质评比课的几点思考
2021-09-06浙江省宁波市第四中学315016蒋亚军
浙江省宁波市第四中学 (315016) 蒋亚军
贵州省安龙县2020年春季高中数学优质课评比在安龙一中举办,笔者作为支教教师有机会参与到听课环节,课题为《1.1.2余弦定理(第一课时)》.参赛的六位选手精心准备,呈现了精彩的设计.本文以听课者的视角对情境引入、定理推导和课堂小结三个环节进行了以下几点思考.
思考1:如何创设合适的情境
情境引入1:以杭州淳安的千岛湖图片,设计三个小岛分别是A、B、C,一名游客想从A岛直接到C岛,已知AB=6km,AC=3km,∠B=120°,却不知道BC距离究竟是多长,你能帮他算一算吗?
情境引入2:多彩贵州有很多隧道,技术人员在修建每个隧道前(打通前)都需要确定隧道长度.其方法是:先在地面上选一适当位置A,量出A到山脚B、C的距离,再利用测量仪器测出的大小,最后通计算求出山脚的长度BC.大家想知道工程技术人员是怎样计算出来的吗?
评注:《普通高中数学课程标准(2017年)解读》指出,基于核心素养的教学,要特别重视情境的创设和问题的提出.情境可以包括:现实情境、数学情境、科学情境[1].参赛的六位选手都是从现实情境出发,将生活中的问题抽象转化为数学的问题,联系学生已有的知识正弦定理,发现正弦定理不能解决这类问题,产生认知上的冲突,激发学生的求知欲,顺利引入本课题余弦定理.相比较很多学生对千岛湖的不熟悉,引入2更贴近学生的生活,通过教师有意识的讲解,学生对美好家乡美好生活感到自豪.解三角形的产生和发展就是解决现实生活中测量三角形的边和角,使几何与代数有机的结合起来,进而促进三角函数的发展,正弦定理和余弦定理不仅是解决三角形中定边定角的有力工具,而且是对初中全等三角形的定性判断上升到了定量计算.遗憾的是很少有选手从整体教学的角度去思考这一问题,帮助学生编织相互联系的知识网络.
思考2:余弦定理公式的推导
在△ABC中,已知AB=c,AC=b,角A,求BC边a.
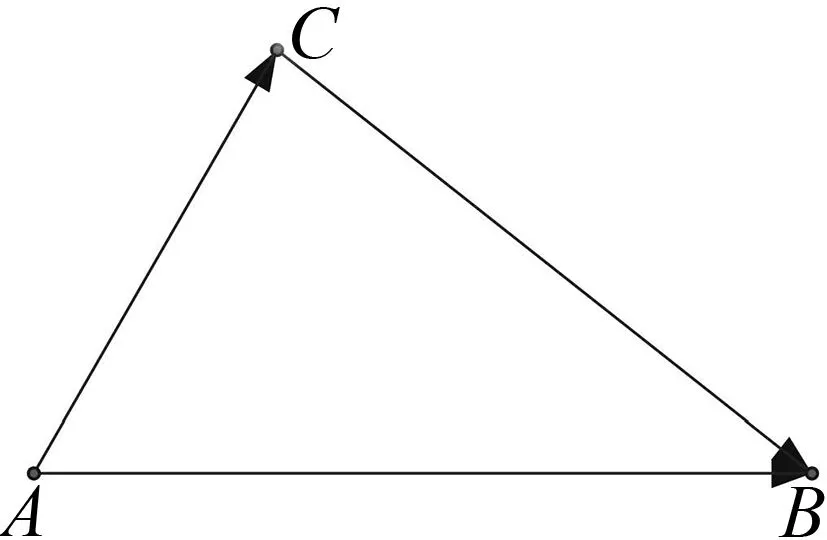
图1
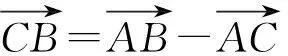
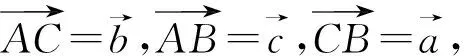
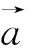
公式推导3:(1)当∠A是直角时,a2=b2+c2=b2+c2-2bccos90°=b2+c2-2bccosA.
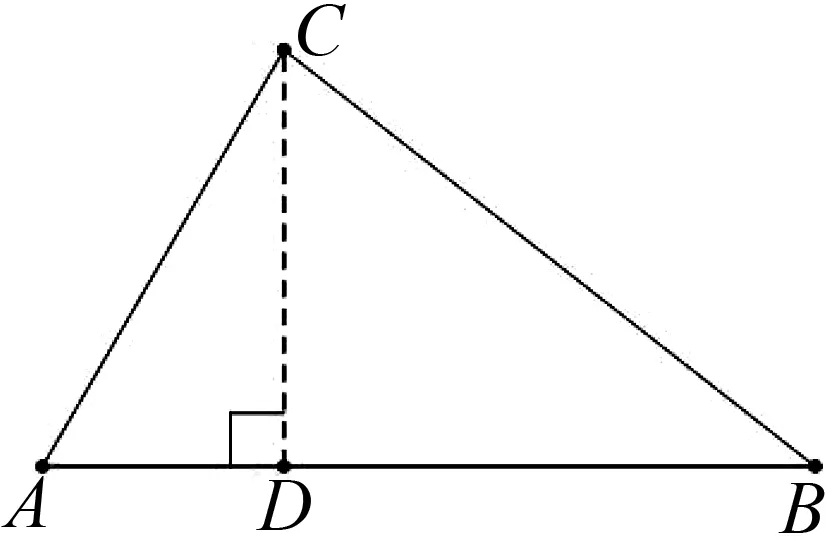
图2
(2)当∠A是锐角时,如图2,过点C作CD⊥AB,交AB于点D,则在Rt△ACD中,AD=bcosA,CD=bsinA.从而,BD=AB-AD=c-bcosA.在Rt△BCD中,由勾股定理可得BC2=BD2+CD2=(c-bcosA)2+(bsinA)2=c2-2cbcosA+b2,即,a2=b2+c2-2bccosA.
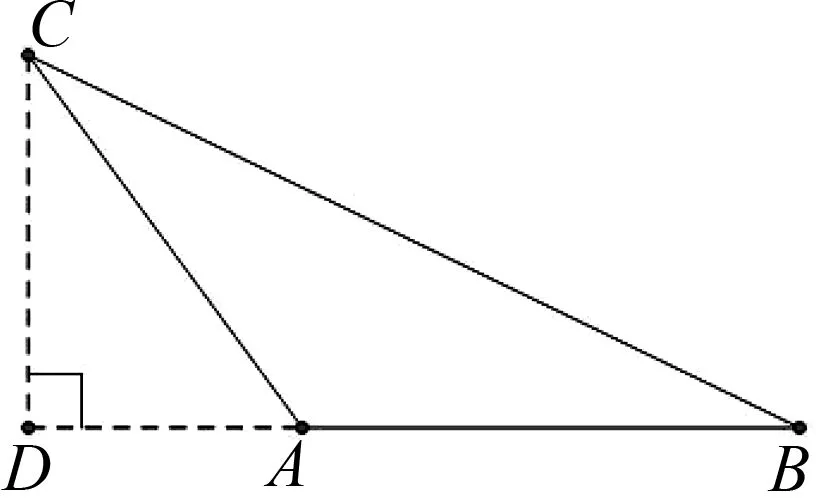
图3
(3)当∠A是钝角时,如图3,过点C作CD⊥AB,交BA延长线于点D,则在Rt△ACD中AD=bcos(π-A)=-bcosA中,CD=bsin(π-A)=bsinA.从而,BD=AB+AD=c-bcosA.在Rt△BCD中,由勾股定理可得BC2=BD2+CD2=(c-bcosA)2+(bsinA)2=c2-2cbcosA+b2,即a2=b2+c2-2bccosA.
综上(1),(2),(3)可知,a2=b2+c2-2bccosA成立.
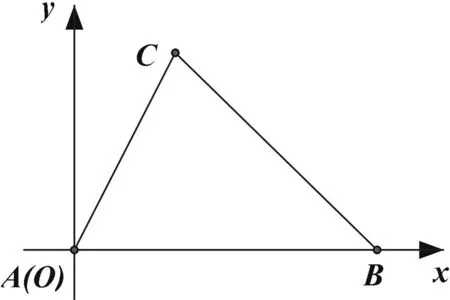
图4
公式推导4:建立平面直角坐标系(如图4),则由题意可得点A(0,0),B(c,0),C(bcosA,bsinA),再由两点间距离公式可得a2=(c-bcosA)2+(bsinA)2=c2-2cbcosA+b2.即a2=b2+c2-2bccosA.
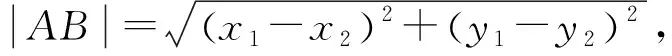
思考3:设计有新意的课堂小结
课堂小结1:通过本节课的研学习,同学们学到了那些知识和方法?有何体会?(学生自我总结,教师适时补充完善)
1.余弦定理及其推论.
2.余弦定理可解决两类解三角形问题:一是已知三边,二是已知两边及其夹角.
3.用向量法证明余弦定理,体现了数形结合思想.
课堂小结2:在师生共同完成知识、方法、数学思想的小结后,教师赋打油诗一首:
解决三角形,边角是关键
正弦加余弦,余弦可求边
正弦边角化,定角用余弦
综合正余弦,三角化简便
课堂小结3:以框图的形式展现本节课的知识和学习的脉络.
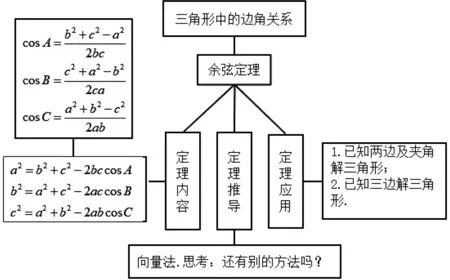
评注:课堂小结是对本节课学习的知识、方法、技能和数学思想的总结,对比三种不同的总结方式,会发现:课堂小结1是教师经常采用的一种模式,通过学生自主回顾总结和教师适时补充完善,有利于学生对学习内容的有效整理,培养学生的表达能力;课堂小结2打油诗一首更是增添新意,引起学生的兴趣,朗朗上口的语言,更利于学生理解和掌握解三角形时的方法选择;课堂小结3以图形的形式再次展现本节课的学习过程,条理清晰思路明确,比文字语言描述更加生动,并且提出一个思考题,学生带着问题离开课堂,通过查找资料、分工合作,有效地将课堂延伸,激发学生的学习热情和学习兴趣.
数学学科核心素养是数学课程目标的集中体现,是具有数学特征的思维品质、关键能力,以及情感态度价值观的集中体现,是在数学学习和应用的过程中逐步形成和发展的[2].而核心素养的培养,既要使学生习得数学知识,更要让学生经历数学研究的过程,体验隐藏在背后的数学思想方法以及研究方法[3].教师在课堂教学中应当结合教学内容,设计合适的问题情境,引导学生用数学的语言表达问题,培养发现和提出问题的能力,分析和解决问题的能力,在余弦定理公式的推导过程中一点要舍得花时间让学生思考和探索,给予学生展示思维活动的机会和平台,激发学生多角度深层次的思考问题,关注学生对数学知识真正的理解.从而达到学生对“冷艳”的数学进行“火热”的思考的目的.有新意的设计课堂小结,如打油诗形式、框图形式以及设计成一个卡通图案,会给学生一种视觉上的冲击,产生新鲜感,促进学生的理解和掌握.
