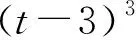优化高三数学复习课教学的实践与思考

江苏省锡山高级中学 (214174) 马晴燕

基于核心素养的教学策略，需要我们更多地关注如何从知识点的落实转向到素养的养成，如何从关注“教什么”转向到关注学生“学会什么”.素质教育倡导回归数学本质,提高学生学习能力,而理解数学是教师教好数学的前提，更是学生学好数学的基础.笔者连续多年的高三教学发现:学生怕教师“炫”各种技巧，希望能倾听他们的想法，考虑他们的立场,多跟他们交流.为此,笔者努力遵循学生的心声,进行了一些尝试,有了以下几点体会.

1、遵循学情合理选择和呈现教学内容，引动学生参与学习

好电影要有好的导演和编剧,高效的课堂离不开教师的合理规划.首先,高三的教学更适合教师尝试单元化设计、分解课时，根据所教章节在对应知识体系中的地位和作用合理选择、安排教学内容,力求前后自然承接、突显教学重点.其次,教师能根据学生知识现状,将教学内容设计成学生易于接受并参与学习的呈现形式，让学生自然地参与学习，有效分解教学难点.

案例1 复习课中与二次方程、二次不等式有关的恒成立、有解问题学生掌握不熟练，不少学生对这些知识掌握呈碎片化，而孤立的、缺乏知识系统性的知识点训练也导致训练效果不佳，学生综合运用知识的能力不强.因此教师尝试将一段时间内接触的有关问题整合后再呈现给学生.

引例已知M={x|x2-3x-4≤0}，N={x|x2-6x+9-m2≤0}，若M⊆N，则m的取值范围是________________.

此题入口较宽，解不等式易忽略对m的讨论，构造二次函数图像更简洁.

变式不等式x2-6x+9-m2≤0对x∈[-1,4]恒成立，求m的取值范围.

可解不等式或考虑(分参)转化为函数最值来解，提示学生发现其与引例相同.在此基础上设计以下例题.

例1 已知M={x|2x2+mx-1<0}，根据下列条件求实数m的取值范围.⑴(0,3)⊆M；⑵M∩(0,3)≠∅；⑶(0,3)⊇M.

例2 根据下列条件求实数m的取值范围.(1)∃x∈{x|-1

课后结合课堂给出类似题组训练.分别求满足下列条件的a的取值范围.(1)[0,3]内每个x都满足不等式x2+2(1-a)x+3-a≤0;(2)[0,3]内存在x满足不等式x2+2(1-a)x+3-a≤0.这样把学生容易混淆的几种类似问题适当改编，按照学生的实际水平从易到难层层递进，引导着学生逐渐参与学习和探究，学生更易找到知识之间的关联和区别，在解惑同时巩固了函数与方程、数形结合、转化与化归思想，自然地提升了数学逻辑思维能力和抽象概括能力.

2、遵循学生思维发展规律，融入学生中去倾听和交流

优秀的导演懂得分析演员的特质，能引导演员共同打磨角色.称职的教师应该认识学生的学习特点，遵循学生的发展规律，努力唤起学生学习的能动性,尽量避免无效“代劳”,为此，教师应努力做到以下两点.

2.1 诊断教学中学生可能有的表现，做好预设便于倾听和交流

教师深入解读2017版课程标准，基于所涉及数学知识的核心概念和数学本质，分析学生的认知基础和思维发展规律，结合教学经验预测学生可能有的障碍和表现，预设教学障碍及应对策略，让教师在课堂上更合理的倾听、更自然的介入引导和交流.实践证明，必要时教师可通过抽样询问学生、跟同事交流等方式，为课堂的有效倾听和交流奠定基础．实际教学时，教师基于预设，结合实际教学状况灵活调整教学，合理引导学生展开思考，促进师生自然交流.

案例2 若将函数f(x)=x3表示为f(x)=a0+a1(3+x)+a2(3+x)2+a3(3+x)3,其中a0，a1,a2,a3为实数，则a1=________________.

此题涉及的核心数学知识主要有函数、导数和恒等式，常用思想方法是转化与化归.据经验，极少学生会求导后赋值-3，分析实际预测学生可能的想法依次是特殊化或展开利用恒等式，教师课前研究这两个方法的优劣和联系，预备引导学生反思恒等式的常见处理方式，提问学生会求a0,a3吗？a0,a3为什么易求?a1能类似求吗？自然地引导学生有效思考，教师边倾听边提示，促进师生和谐交流.从而有了以下的教学实录.

2.2 尊重学生的实际思维水平,诚心、耐心、专心、细心地倾听和交流

教师教学、解题经验丰富，备课时对问题已有所思考，而学生刚接触问题，需要一定的思考时间和尝试的空间.教师应积极为学生创设良好的思考环境,根据多数学生的探究情况，结合诊断进行二次备课，请学生对普遍解法表述分析过程(为什么这么想)、展示解题过程(具体怎么做)，请其他同学不断补充(优劣在哪里)，一边耐心倾听一边多追问(合理吗？都这么想的？)努力倾听广大同学的真实心声.若是讲评课,教师可借助批阅设备统计、分析学生的解答，课堂上请有代表性的同学或者小组进行具体思维过程的展示.

可见,教师依据深入调查所获的学生实际思维水平，为学生提供合理的思考时间和空间是学生发展思维的保证.诚心专注地倾听利于提升学生表达欲望，切实为学生提供充裕的表达机会;让交流更融洽，站在学生的立场去分析和思考，参与学生的学习过程.师生和谐共进以获得更多有价值的教学成果，提升课堂发展．

3、配合学生反思总结,促进养成批判性思维的习惯

师生共同探讨的结果,教师应及时配合学生进行批判性思维，从错误和不完美中积累经验，形成学生自己的思维定势.通过案例3,就有了以下案例4的表现.

通过对知识点、解题策略等的不断回顾，让学生养成及时反思总结的习惯,有利于培养学生思维的批判性和严谨性,提升学生的数学素养和数学学习能力.

4、引导学生系统梳理所学，回归数学问题本质

经过了预设、倾听、交流、反思之后，教师应抓住契机引导学生进行更系统的梳理，深入理解数学本质，逐渐实现回归问题本质与遵循学生学情的统一.这一过程渗透在上述两点中，寻找教学内容和学生认知基础的衔接点，旨在系统认识知识的本质和找到学生的最近发展区域；融入学生中去共同学习旨在落实遵循学生实际和把握数学本质，协助学生养成良好的学习习惯.

学生思路二：以A为原点建立坐标系，分别设B(a,b),C(c,d)，代入求出D坐标(学生理由是字母多，建立坐标系后直接运算).

学生思路三：以M为坐标原点，BC所在直线为x轴建立平面直角坐标系，则B(-5,0)，C(5,0)，M(0,0)，A(x,y)，且x2+y2=9，代入坐标即可.

学生思路四：特殊化A点位置，比如AM⊥BC.

在教学中，教师应对学生的反思进行查漏补缺，引导他们系统梳理并努力回归数学本质，形成完整的知识脉络，体悟运用的数学思想方法.实践证明，相比教师直接总结,坚持引导学生尝试自我反思、系统梳理，更有利于学生养成独立思辨、自主概括的良好学习习惯.为此，教师要舍得花时间，并花合理的时间引导学生去系统梳理、总结提升，进一步发挥数学教学的育人价值.

多年高三教学实践证明，课堂教学应切实尊重学生实际,多倾听、细交流、深反思、勤梳理，努力追求数学本质和学生实际的有效融合,促进学生数学学习的有效发展.在此过程中教师应多角度的寻求认知的深化，引导学生更透彻把握数学的本质.总之，新的课程改革在高三应有良好的实践环境，教师应对比新老教材，将优化数学教学的实践和深入解读课标有效融合，努力追求“切实尊重学生、真正理解数学、有效落实课标”的目标，扎扎实实的推进新课程改革，落实“四基、四能”的培养目标，有效发挥数学学科的育人价值.