以“练”促“习”,撬动思维的齿轮
——《长方体和正方体的认识》(练习课)教学思考
2021-09-03阮传忠
○阮传忠
(作者单位:安徽省合肥市锦绣小学)
练习课是新授课的补充和延续。教师应努力让练习课超越知识和技能的训练,从关注“学会”到关注“会学”,从而帮助学生在“练”中“习”得认知上的拓展与思维品质的提升。
一、以“练”促“习”,强化认知基础
师:如图所示,你能想象出这个长方体的样子吗?试着画一画。
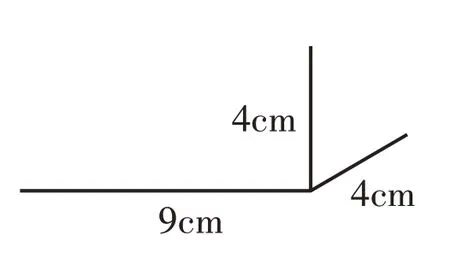
生:(边画边说)先根据长和高想到了长方体的前面,接着根据宽和高想到了长方体的右面,又因为对边的棱相等,最后根据长和宽想到了上面。
师:在还原长方体的过程中,要抓住什么重要条件?
生:长、宽、高。
师:接下来,根据图中的已知信息提出问题并解答。
生:我提出了长方体的棱长总和是多少,算式是(9+4+4)×4。
师:(指着算式中最后的数字“4”)这个“4”是什么意思?
生(齐):4组长、宽、高。
只有抓住了几何体基本的结构特征,才能认清它的全貌。长方体(正方体)的结构特征取决于它的长、宽、高(棱长)。在教学中通过相交于一个顶点的三条棱,让学生借助想象建构表象。学生只有“脑中有形”,才能做到“眼中有物”。同时在重构表象的过程中,让学生思考每个面与对应棱之间的关系,从而进一步加深对面、棱、体三者之间关系的理解,并在边说边画的过程中,手脑并用,强化认知基础。
二、以“练”促“习”,沟通知识联系
师:从这个长方体中挖去一个最大的正方体,剩下部分的体积和表面积与原来相比,发生了怎样的变化?试着画一画,并列式解答。
生:挖去一个最大的正方体,要用短边作正方体的棱长。
师:挖后剩下的体积有没有变化?是怎么变化的?
生:少了一个正方体,正方体的体积是43=64(cm3)。
师:表面积呢?
生:(边指边说)长方体少了一个面,但是切割后剩下的部分又多了一个面,所以一共减少了4个面。
师:他说减少了4个面?
(其他学生窃窃私语,发表不同意见。)
师:有说4个的,有说5个的,不着急,先想一想。
(教师结合白板动态演示,帮助学生理解一共少了几个面。)
师:这4个面的面积怎么计算?
生:4×4×4=64(cm2)。
练习不仅巩固知识、提高技能,更要沟通知识的内在联系,构建完整的知识体系。片段中,教师提出的问题巧妙地将长方体与正方体的特征、表面积与体积各个独立的知识点进行有机联系,从而引发有意义的思维活动。试想学生要正确挖出一个最大的正方体必须思考:正方体的棱长是多少合适?要解决以上问题,需对这个长方体长、宽、高进行观察与分析。而挖取前后表面积和体积的变化比较,则是对表面积和体积本质的进一步追问。这一点从学生的课堂回答中也能得到佐证,大家都同意体积减少了一个正方体的体积,但在表面积的变化上,一开始出现了两种不同的声音(4个、5个),这也说明学生在这方面缺乏一定的空间想象能力,而这正是“图形与几何”教学的重难点。
三、以“练”促“习”,提升思维品质
师:从这个长方体中挖去一个棱长为2cm的正方体,剩下部分的体积和表面积与原来相比,又发生了怎样的变化?试着画一画、算一算。
生:我挖在棱上。
师:“棱上”是什么意思?
(学生示意位置,明确含义。)
生:体积少了一个小正方体的体积,表面积增加了2个面的面积。
(借助白板动态呈现挖小正方体的过程。)
师:(指图再解说)减少了几个面?但同时又增加了几个面?
生:(指着示意图)左面平移至原来的右面,下面平移到上面,还剩前后2个面,所以最后增加了2个面。
(利用动画演示面的平移过程。)
生:如果从顶点处挖去一个小正方体,它的体积减少了23=8(cm3);表面积没有变化,因为它的上面、前面、右面各少了一个面,但下面、后面、左面又多了一个面。
(结合白板动态呈现挖的过程。)
师:少了3个面,但是又多了3个面,(动态演示面的平移过程)所以表面积没有变化。
生:我是挖在面上。(结合白板动态呈现挖的过程)这样就少了1个面,与此同时又多了5个面,所以它的表面积最终增加了4个面的面积。体积还是少了1个小正方体的体积。
师:回顾一下刚刚的解题过程,你有什么发现?
(师生共同梳理并完成如下表格。)
位置 体积变化表面积变化减少的面 增加的面 最后变化
师:仔细观察表格内容和数据,你有什么新的发现?
生:一共有三种不同的挖法,它们的体积变化是一样的,但是它们的表面积变化不同。所以说,看你选择什么样的挖法,不同的挖法表面积是不同的,但体积变化只有一种。
练习中,并不是学生的想法越多越好,而是每名学生是否真正参与了思考,是否在倾听、思考与比较中让自己原有的想法更加深入。片段中,通过设计“剩下部分的体积和表面积与原来相比,发生了怎样的变化”这一开放性的问题,满足了不同水平学生的学习需求,每个人基于自己的认知水平和经验对问题进行思考。同时,通过小组的展示与交流,每个人又在不断地刷新自己原有的认知结构。最后,通过整体的展示、比较与分析,让学生在识破各种挖法的惊喜中,逐步梳理出变中不变的规律,从而实现知识的丰盈和思维的提升。
