高压共轨燃油系统喷油量的预测模型

2021-08-31梁勇费红姿刘冰鑫柳一林朱腾飞

中国舰船研究 2021年4期

梁勇，费红姿，刘冰鑫，柳一林，朱腾飞

哈尔滨工程大学，动力与能源工程学院，黑龙江哈尔滨，150001

0 引言

为了减少船用柴油机的排放、提高柴油机的经济性及增强动力性能，有必要对柴油机喷射燃油量（以下称喷油量）予以精确控制[1-2]。为此，国内外学者提出了许多控制方法和策略，但多数都是基于MAP 图对喷油量基本值进行补偿修正。例如，Samuel 等[3]提出基于发动机转速和驾驶员输入的针对每个循环燃油喷射时间、持续时间及喷射次数的控制策略，其控制算法可在线校准发动机MAP；林学东等[4]提出的共轨柴油机启动工况高压泵控制策略需要喷油MAP 组成前馈控制模块；丁晓亮等[5]提出基于集总模型的周期函数计算修正油量，其中，主喷油量波动幅值仍通过MAP 图获得；仇滔等[6]使用发动机转速、当前共轨压力（以下称轨压）和喷油量的MAP 进行前馈轨压控制，以此稳定压力波动，实现精确喷油。

在多数燃油控制策略中MAP 图都起着关键作用，但需通过大量试验才能获得。对于连续喷射情况，随着喷油间隔时间的变化，喷油量会产生波动，而为能够反映波动情况，针对不同工况下的波动油量的MAP 试验成本也极大地增加。

鉴此，本文将针对预-主喷模式(含1 次预喷和1 次主喷)建立基于间隔时间、轨压和主喷脉宽输入参数的主喷油量波动预测模型，旨在减少传统MAP 图方法对大量试验的需求，并保证高预测精确。首先，运用AMESim 仿真模型，通过模拟获取大量数据，得到单一工况下的间隔时间与主喷油量之间的关系；然后，考虑轨压和主喷脉宽对模型系数的影响，构建多工况下的主喷油量波动预测模型；最后，使用多组不同组合的输入参数，验证所提模型的准确性和可靠性。

1 主喷油量预测模型构建方案

1.1 基于AMESim 的高压共轨系统模型

本文针对含4 个喷油器的某型高压共轨燃油系统，建立了AMESim 仿真模型，如图1 所示。该仿真模型包括4 个部分：高压油泵、电控喷油器、电控单元(ECU)和共轨管。其中，共轨管右端有轨压控制器（PI 控制器），可将信号传输至油泵，以调节轨压，使其在喷油后依然能够在一定范围内保持稳定。通过设置喷油脉宽，调整ECU 发出的信号，进而控制电控喷油器的喷油量。本文用于研究并建立主喷油量波动预测模型的数据均通过此AMESim 模型模拟试验得到。

图1 高压共轨燃油系统AMESim 仿真模型示意图Fig. 1 Schematic diagram of AMESim simulation model for high pressure common rail system

为了验证AMESim 仿真模型的准确性和可靠性，在轨压为40，100，160 MPa、喷油脉宽为1 800～2 480 μs 的区间内进行试验与仿真。图2 所示为不同工况点的喷油量试验值与仿真值的对比曲线图。由图可见，仿真值与试验值总体变化趋势一致，仿真数据与试验数据吻合度较高，最大偏差9%。考虑到建模时对实际燃油系统的近似、仿真中数值方法求解导致的截断误差，以及试验中偶然因素引起的随机误差，仿真对比试验数据的偏差在可接受范围之内。因此，本文选用该模型进行仿真研究，所得数据可以满足构建预测模型的研究需要。

图2 喷油量试验值与仿真值对比曲线图Fig. 2 Comparison graph of experimental and simulation values of fuel injection volume

1.2 主喷油量波动现象分析

在适合的控制策略和设定的轨压及喷油脉宽下，实际的高压共轨燃油系统单次喷射喷油量符合期望要求，而预-主喷射时控制喷油量的效果欠佳，主喷油量通常偏离期望值。在预-主喷情况下，主喷油量会受到预喷的影响而出现有规律的波动。经过AMESim 仿真实验分析，喷油后燃油系统内产生的压力波动是导致出现上述偏差的主要原因。

在喷油器连续喷射时，前次喷油的关键动作（球阀（控制阀）的开启或关闭和针阀运动）会产生压力波。此时，压力波在喷油器-高压油管-共轨管中的反射叠加，使喷油结束后燃油系统内仍存在压力波动[7]。图3 所示即为喷油器入口处的压力测量结果。由图可见，喷油器入口处的压力在喷油结束后，仍在85～115 MPa 范围内波动，且随着时间的推移呈现了幅值递减的振荡趋势。

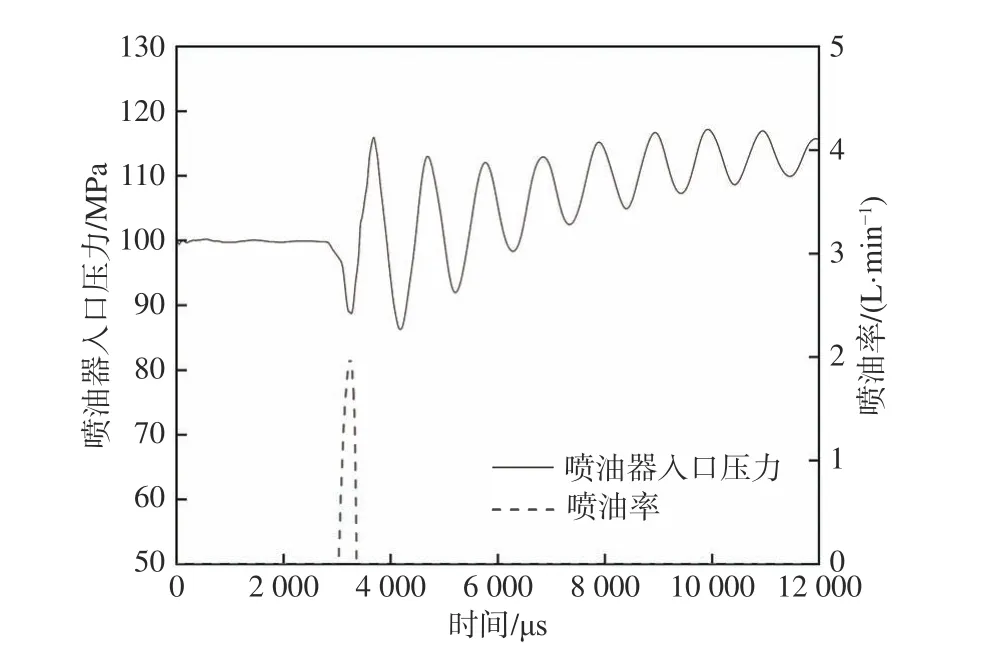
图3 喷油器入口压力和喷油率曲线（喷油脉宽400 μs）Fig. 3 Curves of injector inlet pressure and injection rate when injection pulse width is 400 μs

在喷油结束后，高压共轨系统中的压力变化将影响下次喷射。例如，在预-主喷模式下，预喷后产生的压力波动会导致主喷喷油量出现偏差，且预喷与主喷的间隔时间不同，而主喷开始时，针阀所处压力环境和喷油量也不相同[8]。喷油器喷油时，其入口处的压力被称为开启压力，此压力对应于主喷起始时刻预喷产生的压力波动曲线上的压力值。因此，随着间隔时间的增加，主喷起始时刻相对于预喷发生后移，该时刻预喷压力波动曲线上对应的压力点位置呈波动式后移。

具体而言，开启压力会影响到喷油器中针阀的运动特性，进而改变喷油的持续期和针阀开启高度，最终决定了喷油率，是影响主喷喷油量的关键因素，其与主喷油量存在着相关性。在喷油器开启压力大的情况下，针阀开启提前而关闭延迟，喷油持续期延长，同时由于针阀抬起速度快，使得喷孔更快地到达最大有效截面积，从而增大喷油率，导致喷油量较大[9]。如图4 所示，当轨压为100 MPa、预喷脉宽为400 μs、主喷脉宽为1 000 μs时，不同间隔时间的开启压力和主喷油量出现了波动。由图可见，开启压力与主喷油量变化规律相似，主喷油量随着间隔时间的变化呈现了幅值衰减的周期性波动。分别测量主喷油量波动曲线和开启压力波动曲线两个相邻波峰间的间隔时间，可知主喷油量波动的周期与开启压力波动周期相同，均为1 100 μs。

图4 开启压力与主喷油量波动图Fig. 4 Fluctuation diagram of opening pressure and main injection volume

1.3 预测模型建立过程

综上所述，在确定预喷的情况下，主喷油量是随着间隔时间出现波动的。因此，为了更精确控制主喷油量，建立的主喷油量波动预测模型应包含轨压和主喷脉宽、间隔时间这3 个输入参数。此时，建模所需的数据远少于常规MAP图，同时还保证了模型的实用性。图5 所示为建立的多工况主喷油量波动预测模型方案的流程。图中，单一工况下预测模型的自变量为间隔时间t，将单一工况下预测模型的系数(包括主喷油量波动的幅值a、随间隔时间波动的主喷油量波动频率b、初始相位c、轨压调节过程的系数d、主喷油量的基本值e)表示为轨压Pr和主喷脉宽ET的函数，从而得到多工况（不同Pr和ET）下的主喷油量波动预测模型；然后，再根据喷油原理，对系数的函数关系进行适当的简化。

图5 主喷油量预测模型建立流程图Fig. 5 Flowchart of establishing main injection volume prediction model

建立主喷油量预测模型的详细过程如下：

首先，建立单一工况(确定的轨压和主喷脉宽)下的主喷油量随间隔时间波动的预测模型。在预-主喷的喷射模式下，主喷油量随着间隔时间的变化呈现周期性的波动，其波动方式类似于衰减的正弦函数形状。单一工况下的主喷油量预测模型表示如下：

式中，Q（t）为间隔时间的主喷油量，mm3。考虑到仿真模型中是通过轨压控制器来调节轨压的，并会影响到喷油量，故还引入了d*t项。在k组不同间隔时间内，通过试验得到喷油量，再利用该试验数据对Q(t)关系式的系数予以辨识，进而得到单一工况下的主喷油量预测模型。

然后，求解出式(1)中各系数关于轨压和主喷脉宽的函数关系，即可将这些因素对主喷油量的影响引入到预测模型中。本文研究旨在提出能够以尽量少的试验数据来建立多工况主喷油量预测模型的方案。因此，为了使预测模型具有足够好的准确度，选取了应用工况范围内的几何中心(Pr0,ET0)作为中心工况点。选取该中心点有助于后文的系数辨识过程。

在不同工况下，式(1) 所示主喷油量波动预测模型中的所有系数都会变化，但每次拟合喷油量波动曲线时都同时能够得到所有系数的值。获取的各系数关于轨压和主喷脉宽的函数关系也都可以采用相同处理方式。这里，以系数a来说明模型系数的获取过程，如图6 所示。

图6 模型系数获取示意图Fig. 6 Model coefficient acquisition diagram

由图6 可见，轨压和主喷脉宽的不同组合分别对应一个系数a值。为了减少试验成本，本文利用图6 中穿过中心工况点(Pr0,ET0) 的a1和a2两条曲线来表示整个a曲面，即表示a系数关于轨压和主喷脉宽的函数关系。

a函数曲面在中心工况点(Pr0,ET0)处展开，由式（2）表示中心工况点附近的a函数。

式中：A1，A2分别为轨压和主喷脉宽对a值的影响；C0为其它因素对a值的影响。

主喷脉宽取ET0时，改变轨压，取以Pr0为中心的n个Pr值，拟合数据点，得到关于Pr的函数关系式a1：

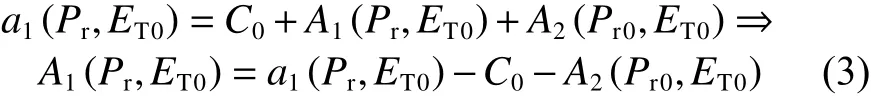
轨压取Pr0时，改变主喷脉宽，取以ET0为中心的m个ET值，拟合数据点，得到关于ET的函数关系式a2：

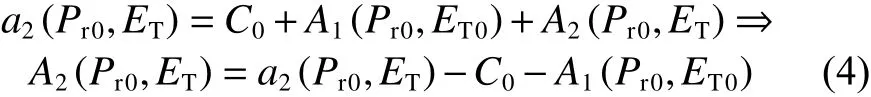
将式(3)和式(4)代入(2)中，得到：

式中，C为一个常数。

由此，采用式（5）得到如下各系数关于轨压和主喷脉宽的函数关系：

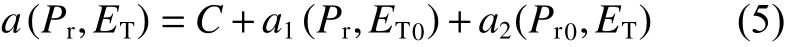
式中：a1(Pr,ET0)为固定主喷脉宽ET0时系数a与轨压的函数关系；a2(Pr0,ET) 为固定轨压Pr0时系数a与主喷脉宽的函数关系；考虑到a1，a2拟合函数会带来一定误差，a1(Pr,ET0) 和a2(Pr0,ET)与原先的系数a不一定相等，故采用代入中心工况(Pr0,ET0)到式(5) 求解的方法来确定常数C，以保证最终a函数的准确度。

最后，将各系数的函数关系式代回到单一工况下的预测模型，即得到式（6）所示完整的多工况主喷油量预测模型Q(t，Pr，ET)。

根据上述建立的预测模型方案，可以仅用k*(m+n-1)组试验数据建立关于间隔时间、轨压和主喷脉宽这3 个参数的主喷油量波动预测模型。相比于传统的MAP 图方法需要的k*m*n组试验数据，本文建立模型需要的试验量由n3量级降至了n2量级，可极大地降低试验成本，提高模型的工程应用性。

1.4 预测模型参数简化

为了更多地降低构建预测模型的工作量，还可以根据现有的共轨系统连续喷射原理性相关研究，分析并适当简化建模过程。若实际物理过程中预测模型的输入参数（轨压或主喷脉宽）对模型的某系数无影响，可省略。例如，通过理论分析和试验，发现主喷脉宽对系数c的影响较小，因此可将式（6）中的c(Pr，ET)简化为c(Pr)。

在喷油脉宽固定的情况下，轨压变化对主喷油量模型系数的影响大体可以分为2 个方面：

1）轨压会影响预喷射造成的压力波动规律，增大的轨压导致压力波动频率和振幅增大。如此，即使间隔时间和主喷脉宽都不发生变化，主喷射的开启压力依然会出现改变，进而影响喷油量，使主喷油量波动曲线的幅值、频率和相位都相应地有所变化。

2）轨压值较大程度地决定了喷油器喷孔前后的压力差，轨压大时，喷孔前后压差和喷油率较大。增加轨压还将使不同轨压下的喷油量波动幅度之间的差异被放大[10-11]。对于本研究使用的仿真模型，预喷喷油量较少而主喷油脉宽相同时，设定轨压值变化对表示喷油后轨压调节过程的d系数影响较小，故可以忽略。因此，轨压对喷油量的影响主要体现为改变该预测模型的a，b，c，e系数。

然而，在轨压固定的情况下，喷油脉宽变化对主喷油量模型系数的影响则体现在如下方面：

1）喷油后的压力波动幅值随时间逐渐减小，在更长的主喷油持续期内，趋于平缓的压力波动所引起的主喷油量波动幅值更小。

2）主喷油量波动的频率由预喷后的压力波动频率所决定，与主喷脉宽无相关性。

3）其它条件不变而仅改变主喷脉宽，这对主喷油量随间隔时间波动的曲线相位基本上不构成影响[12-13]，而其对主喷油量的影响主要体现在该预测模型的a，d，e系数的变化上。

实际应用式(1)后的结果显示，在不同的轨压和主喷脉宽情况下，拟合得到的主喷油量随间隔时间的波动与曲线中的波动频率系数b（主喷油量波动频率b）之间的差别较小。因此，为了简化建立的预测模型，本文忽略了轨压和主喷脉宽对系数b的影响，而以常值代替。式（7）即为简化后的多工况主喷油量波动预测模型Q(t，Pr，ET)。

2 主喷油量波动预测模型建立结果

2.1 单一工况主喷油量波动预测模型的建立与验证

式(1)所示的单一工况下主喷油量波动预测模型包括了a，b，c，d，e这5 个模型参数，还需要对这些模型参数进行辨识，才能得到能准确描述间隔时间与主喷油量间关系的模型。本文以预喷脉宽400 μs、主喷脉宽1 200 μs、轨压110 MPa 的工况为例，对间隔时间从600～4 000 μs 的喷油进行仿真模拟试验。为此，将采集的35 个数据点划分为两组，一组用25 个仿真数据点来辨识该工况下的主喷油量预测模型，另一组用10 个仿真数据点来验证该主喷油量波动预测模型的准确度。

利用上述工况点，运用最小二乘法对待辨识的数据组进行曲线拟合，得到的系数如下：a=1.56，b=0.006 074，c=0.874 1，d= 0.000 911 8，e=60.71。图7 为曲线拟合的结果，拟合曲线的均方根误差RMSE=0.358 1 mm3，决定系数R2=0.947 3，该模型系数的辨识结果较好。

图7 模型拟合结果Fig. 7 Model fitting results

使用经过最小二乘法拟合得到的模型对验证数据组的喷油量进行预测，并对预测结果与仿真值的关系进行回归分析，结果如图8 所示。图中，每个数据点的横坐标都表示一个间隔时间下的仿真值，纵坐标都表示用该间隔时间计算得到的预测值，回归线为预测值等于仿真值的直线。由图可见，数据点越是分布在回归线上，模型预测的结果就越接近仿真值，经回归分析得到的R2=0.852 7。这说明在确定的轨压和主喷脉宽情况下，应用式(1) 作为单一工况下的主喷油量预测模型预测有足够高的准确度。

图8 单一工况下主喷油量预测值与仿真值回归分析图Fig. 8 Regression analysis diagram of predicted and simulated values of main injection volume under single working condition

2.2 多工况主喷油量波动预测模型的建立与验证

在不同的轨压和主喷脉宽情况下，主喷油量随着间隔时间变化依然呈现周期性的波动，而模型系数a，b，c，d，e也将随之发生变化。因此，仅在单一工况下得到的预测模型不能满足要求，需要引入变工况因素，找出轨压和主喷脉宽与a，b，c，d，e系数的函数关系，以进一步建立多工况主喷油量波动预测模型。

本节以预喷脉宽400 μs，轨压80～140 MPa、主喷脉宽800～1 600 μs 的工况为预测研究范围，说明建立通用的多工况主喷油量波动预测模型的方法。在上述研究范围的中心工况点（Pr0,ET0）为(110 MPa, 1 200 μs)。

2.2.1 轨压变化对主喷油量波动模型系数的影响

固定主喷脉宽为1 200 μs（研究范围的中间值），令轨压改变，范围为80～140 MPa。与上述构建的单一工况模型相同，以式(1)为拟合函数，采用最小二乘法辨识得到7 个不同轨压下的主喷油量预测模型，并以这7 组预测模型的系数来建立轨压与系数之间的关系。图9 所示为主喷脉宽为1 200 μs 时系数a与轨压之间的关系曲线。

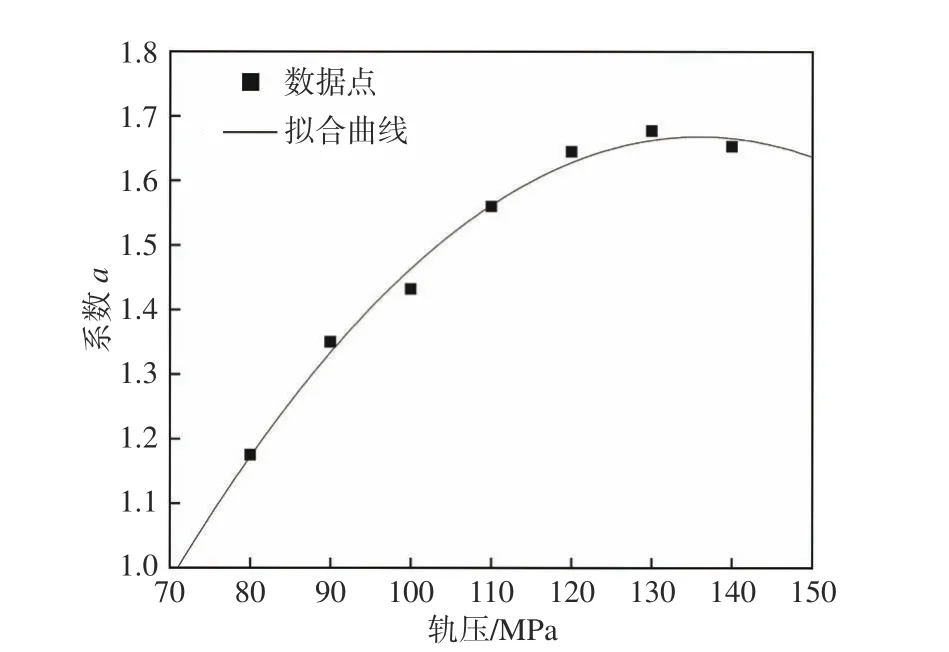
图9 系数a 随轨压变化(主喷脉宽1 200 μs)Fig. 9 Variation of coefficient a with rail pressure when main pulse width is 1 200 μs

对图中数据点进行曲线拟合，得到系数a1拟合曲线的函数表达式为

采用类似方法，可以得到系数c，e与轨压的函数关系，而系数b，d则直接以中心工况点时的系数作为常值，结果如表1 所示。

表1 不同工况下主喷油量波动预测模型系数的计算Table 1 Calculation of coefficient of main injection volume fluctuation prediction model under different working conditions

2.2.2 喷油脉宽变化对主喷油量模型系数的影响

固定轨压为110 MPa（研究范围的中间值），令主喷脉宽改变，范围为800～1 600 μs。以式(1)为拟合函数，采用最小二乘法辨识得到9 个不同主喷脉宽下的主喷油量预测模型，并以这9 组预测模型的系数来建立主喷脉宽与系数之间的关系。图10 所示为轨压为110 MPa 时系数a与主喷脉宽之间的关系曲线。

图10 系数a 随主喷脉宽变化(轨压110 MPa)Fig. 10 Variation of coefficient a with main jet pulse width when rail pressure is 110 MPa

对图中数据点进行曲线拟合，得到系数a2拟合曲线的函数表达式为

采用类似方法可以得到系数d，e与主喷脉宽的函数关系，而系数b，c则直接以中心工况点时的系数作为常值，结果如表1 所示。

2.2.3 组合喷油脉宽和轨压对主喷油量模型系数的影响

研究的工况范围为轨压80～140 MPa、主喷脉宽800～1 600 μs，中心工况点(Pr0,ET0)取值为(110 MPa，1 200 μs)。经式(5)、式(8)和式(9)计算得到的系数a应是相同的。基于此，可以求出对应的常数C=1.561，将式(8)、式(9) 和常数C代回到式(5)中，得到系数a关于轨压与主喷脉宽的函数关系式为

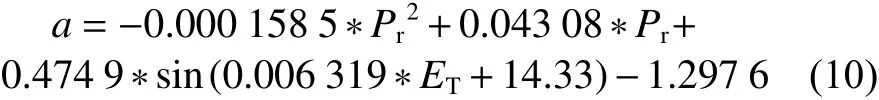
采用上述方法，不仅可获取系数a关于轨压与主喷脉宽的函数，也同样可获得系数b，c，d，e的函数，如表1 所示。将表1 中各系数的函数关系式代入式(1) 中，便可建立完整的多工况主喷射喷油量波动预测模型。

2.2.4 模型预测效果验证分析

为保证模型预测效果验证的有效性，选取不参与模型参数辨识的仿真工况点来检验模型预测的准确度。确定的验证工况点由3×3×4 组数据组成，其中：轨压分别为80，100，120 MPa；主喷脉宽分别为800，1 200，1 600 μs；间隔时间分别为900，1 900，2 900，3 900 μs。

在模型中输入对应的轨压、喷油脉宽和间隔时间参数，将计算得到的预测主喷油量值与仿真值进行回归分析，结果如图11 所示。图中，数据点聚集在回归线上，其中，RMSE=1.443 mm3，R2=0.991 4。由图可见，模型的预测值与仿真值的一致性较好，所得预测效果理想。

图11 多工况下主喷油量预测值与仿真值回归分析图Fig. 11 Regression analysis diagram of predicted and simulated values of main injection volume under multi-working conditions

图12 为主喷油量与仿真值对比结果。图中，前12 组数据点为轨压80 MPa 时的预测喷油量，其中，主喷脉宽1 200 μs 时，4 组不同间隔时间的数据预测误差均小于1 mm3，其它8 组数据的误差最大不超过3.5 mm3。总体上，在靠近中心工况点的主喷脉宽（即1 200 μs）时，无论轨压和间隔时间是多少，预测均能取得极高的准确度；而在较低或较高的主喷脉宽下，通过模型得到的预测值就存在相对较大的误差，尤其是轨压为80 MPa时，主喷油量的预测结果与仿真值间的误差更大。究其原因，在于本文所提建模方案简化了轨压和主喷脉宽与主喷油量的关系，而以线性叠加的方法确定模型参数，从而使得一方面降低了建模的数据需求，另一方面又必然丧失稍许的准确度。实际上，无论是改变轨压还是主喷脉宽，两者中的另一个参数对主喷油量的影响规律也是变化的。

图12 主喷油量值与仿真值对比Fig. 12 Comparison of main fuel injection value and simulatedvalue

综合上述分析，本文所提出的主喷油量波动预测模型有足够好的预测准确度，且越靠近选取的用于辨识模型系数的中心工况点，准确度就越高。该预测模型既可选取高压共轨系统的期望工况为中心工况点，也可进一步考虑轨压与主喷脉宽之间的交互作用对主喷油量的影响，通过适当调整预测模型处于较边缘工况点时的系数，以适应更高的应用精度需求。