高考中的数列求和问题

廖永福

(福建省厦门第二中学 361009)

我们知道，等差数列和等比数列是两类最基本的数列，求通项公式和前n项和是数列的两个基本问题，解答一般数列求和问题的基本思想是根据数列通项的特征，运用适当的方法，把它转化为等差数列、等比数列、或其它可求和数列的求和问题，常用的方法有：公式法、分组转化法、裂项相消法、并项求和法、倒序相加法和错位相减法等.下面以近年高考题为例，阐述如下：

一、公式法

如果数列是等差数列或等比数列，那么它的前n项和可直接用求和公式求得.公式法是数列求和最基本、最重要的方法.

例1(2020·海南)已知公比大于1的等比数列{an}满足a2+a4=20，a3=8．

(1)求{an}的通项公式；

(2)求a1a2-a2a3+…+(-1)n-1anan+1．

分析(1)设数列{an}的公比为q(q>1)，先用基本量法求出a1和q，再求出数列{an}的通项公式；

(2)依题意，数列{(-1)n-1anan+1}是以a1a2为首项，-q2为公比的等比数列，根据等比数列求和公式，即可求出答案．

解析(1)设等比数列{an}的公比为q(q>1)，

所以an=2·2n-1=2n．

点评本题考查等比数列的通项公式、前n项和公式，考查转化思想和方程思想，属于基础题．

二、分组转化法

如果数列的各项是由若干个可求和数列的对应项之和构成，那么这个数列的前n项和可用分组转化法求得，这个数列的前n项和等于这些数列前n项和的和.分组转化法是数列求和常用的方法之一.

解题步骤：(1)把已知数列拆分成若干个可求和的数列；(2)求出各个数列的前n项和；(3)把所得的结果相加.例如，数列{an+b+cqn-1}可拆分成数列{an+b}和{cqn-1}等.

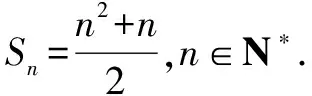
(1)求数列{an}的通项公式；

(2)设bn=2an+(-1)nan，求数列{bn}的前2n项和．

所以数列{bn}的前2n项和为22n+1+n-2．

点评本题主要考查数列通项公式的求法及数列求和的方法，考查学生的运算能力，属中档题．

三、裂项相消法

如果数列的通项可以拆分成两项之差，并且在求和时大部分中间项可以相互抵消，只剩下首尾有限项，那么这个数列的前n项和可用裂项相消法求得.裂项相消法是数列求和重要的方法之一.

解题步骤：(1)把通项拆分成两项之差；(2)写出和式；(3)化简.

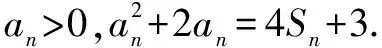
(1)求{an}的通项公式;

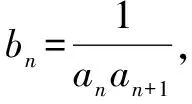
分析(1)根据数列的递推关系，利用作差法可以求出{an}的通项公式；

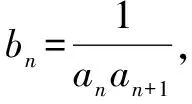
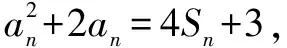
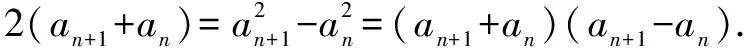
因为an>0，所以an+1-an=2.

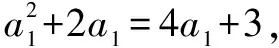
所以{an}是首项为3，公差d=2的等差数列.

所以{an}的通项公式an=3+2(n-1)=2n+1.

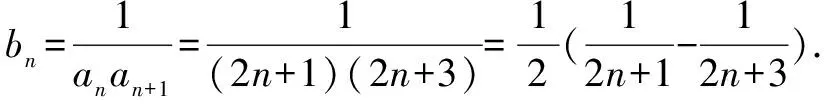
点评本题主要考查数列的通项公式以及数列求和的计算，利用裂项法是解决本题的关键，属中档题.

分组转化法与裂项相消法本质上都是拆：前者是把数列拆分成若干个可以分别求和的数列；后者是把数列拆分成两个大部分项可以相互抵消的数列.

四、并项求和法

如果依次把数列相邻的若干项合并，可以构成一个新的可以求和的数列，那么这个数列的前n项和可用并项求和法求得.并项求和法是数列求和常用的方法之一.

解题步骤：(1)依次把数列相邻的若干项合并；(2)构造新数列；(3)求新数列各项之和.形如{(-1)n(an+b)}的数列、周期数列等求和问题都可用此法.

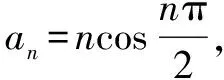
分析易知，数列{an}是周期数列，且周期为4.算出ai(i=1,2,3,4)的值，即可算出所求的结果．

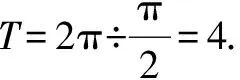
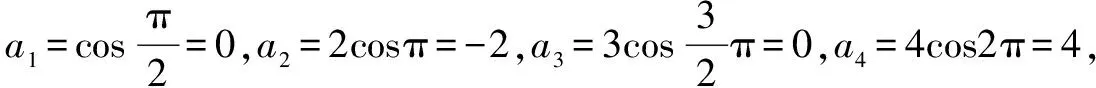
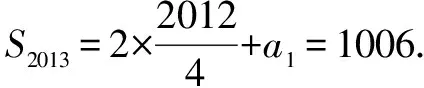
点评本题主要考查数列的求和方法，正确找出数列{an}的周期性是解题的关键，属中档题.

例5(2012·新课标)数列{an}满足an+1+(-1)nan=2n-1，则{an}的前60项和为____．

分析这是一个递推公式中含有(-1)n的数列求和问题，可按奇数项、偶数项分别找出各项之间的规律，进而求出结果.

解析因为an+1+(-1)nan=2n-1，

所以an+2+(-1)n+1an+1=2n+1.

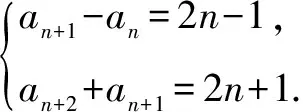
两式相减，得an+2+an=2.

所以S奇=(a1+a3)+(a5+a7)+…+(a57+a59)=2×15=30.

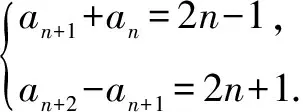
两式相加，得an+2+an=4n.

故{an}的前60项和S=S奇+S偶=30+1800=1830.

点评本题考查数列的递推公式，考查用分组转化法和并项求和法求数列的前n项和，运用分类讨论思想分别找出奇数项、偶数项之间的关系是解题的关键，属中档题．

五、倒序相加法

推导等差数列前n项和公式的方法就是倒序相加法.一般地，如果数列中与首尾等距离的两项之和相等，那么这个数列的前n项和可用倒序相加法求得.倒序相加法也是数列求和常用的方法之一.

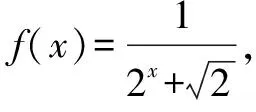
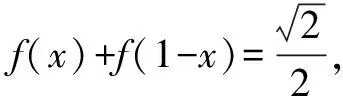
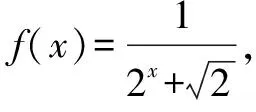
设S=f(-5)+f(-4)+…+f(5)+f(6)，

则S=f(6)+f(5)+…+f(-4)+f(-5).

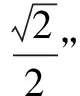
并项求和法与倒序相加法本质上都是合：前者是依次把数列相邻的若干项合并，构成一个新的可以求和的数列；后者是把两个数列(原数列和倒序数列)中的对应项依次合并，构成一个新的可以求和的数列.

六、错位相减法

推导等比数列前n项和公式的方法就是错位相减法.一般地，如果数列的各项是由一个等差数列和一个等比数列的对应项之积构成，那么这个数列的前n项和可用错位相减法求得.即形如{(an+b)qn-1}的数列求和都可以用错位相减法.错位相减法也是数列求和的重要方法之一.

例7(2014·新课标全国Ⅰ卷)已知{an}是递增的等差数列，a2，a4是方程x2-5x+6=0的根．

(1)求{an}的通项公式；

分析(1)解出方程的根，根据递增数列求出a2，a4的值，从而求出通项；

(2)将(1)中求得的通项代入，用错位相减法求和．

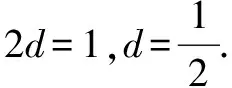
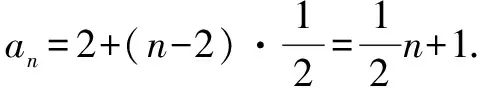
①

②

点评本题考查数列的通项公式和前n项和的求法，利用错位相减法是解决本题的关键，注意解题方法的积累，属于中档题．

综上，尽管数列求和的考查形式千变万化，但是其解法的本质却一成不变，归根结底就是根据通项公式的特征，把一般数列的求和问题转化为已知数列的求和问题.只有灵活掌握所学知识，深刻领会求和方法的思想精髓，才能运用自如，得心应手，真正提升自己的解题能力.