速记巧用三角函数诱导公式

宋朝晖

(新疆喀什第六中学 844000)

高一数学《三角函数》一章，学生感觉内容庞杂，知识点众多，知识间关系错综复杂，难以掌握.还有一个大难题：公式多.学生准确记忆、正确运用有一定的难度.问题最典型的是三角函数诱导公式这一节，很多教师在教授时，都要求学生先背公式，再强行套用公式，勉强完成计算.从心理学角度来说，当一个知识没有被学习者完全理解，对它的记忆是不稳定的.因为不理解，一方面会在使用过程中过于拘谨，表现出僵化教条；另一方面随着学习的推进、新知识的不断涌现，会出现记忆偏差，使得计算错误不断.死记硬背的辛苦，记忆不准确，导致解题失败，消减了学生学习数学的兴趣，打击了学生的自信心.因此，如何让学生脱离记忆公式的痛苦，轻松快速地记住，并灵活应用诱导公式，就成为了一线教师的一项课题.

一、透彻理解诱导公式的推导过程

新课标下，三角函数概念是在单位圆中定义的.为此，诱导公式的推导，是借助单位圆，利用“角的终边的对称关系”来进行的.初学时，经历直观形象的推导过程有助于学生理解记忆公式.如图1，角α终边交单位圆于点P(x,y)，由对称关系知，角 2kπ+α，π-α，π+α，-α的终边与单位圆交点为P1(x,y),P2(-x,y),P3(-x,-y),P4(x,-y).

进而，由任意角三角函数定义可得4组公式：

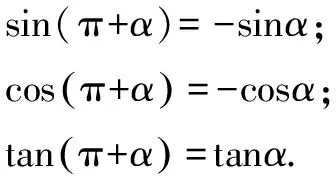
记忆口诀：函数名不变，符号看象限.

记忆口诀：函数名称变，符号看象限.

只要理解到位，结合这两个坐标图去记忆诱导公式组，不失是一种快捷方法.

二、记忆方法对比

1.口诀记忆法

口诀说起来简单，但学生在应用时，还是常常有人不知所措，不会用.调查发现，是学生不明白口诀的真正含义所致.于是将公式直观化，列在坐标系中，演变出如下记忆法.

2.图象记忆法

在图2,3中，能够直观地看到各形式的角应处的象限，确定符号很方便，很准确.学生有了这个图，诱导公式计算化简问题的准确率大大地提高了.

三、巧用诱导公式快速计算

简单的诱导公式计算题学生都能够看着图计算正确，但遇到复杂些、综合性强的计算，学生还会败下阵来.如教材上的这道题：

例1 化简

即使是熟记口诀,熟悉图象的学生，也往往顾此失彼、错误不断.究其原因，如何准确看待这些角，以及化简时使用诱导公式的先后顺序，都影响着结果.

教材上思路是“负化正，正化锐”，把每个因式先统一成诱导公式中的某一形式，再套用诱导公式往下计算.如sin(-π-α)=sin[-(π+α)]=-sin(π+α)=sinα.这种做法，连续多次使用诱导公式，中间环节多，自然增加了学生计算的失误率.

遇到这类题，我教学生这样处理：如图5，先画一个直角坐标系，再把特殊的轴线角标记在对应轴线上，并记住在x轴上则“名不变，符号看象限”，在y轴上则“名称变，符号看象限”.这样原本要多次用诱导公式化简的，只需用一次即完成，大大缩减中间环节.

sin(3π-α)=sinα;sin(-π-α)=sinα;

于是依靠坐标轴，一步就到位.

此法使学生既快又准地得出结果，体验到解题的乐趣.这样对诱导公式进行灵活拓展处理，每一个式子都可以直接用诱导公式口诀化简，大大减轻了计算量，提高了准确率.

sin(α-2π)=sin(-2π+α)=sinα;

cos(2π-α)=cosα.

于是可以口算，原式=sin2α.

再看两个模考或高考例子：

此题后面部分的化简避不开诱导公式的使用，掌握了巧记方法，则可轻松完成.

分析由题意知，函数y=ax+1+2的图象过定点A(-1,3),则tanα=-3.

诱导公式在三角函数有关计算中应用广泛.苦于对繁多的诱导公式记忆不准，学生解三角函数题，难以圆满.巧妙利用画坐标系来记忆公式组，既准确，又方便，还快捷.相比机械的“口诀记忆法”，图象法记忆形象直观，经历的中间过程更少、失误率更低.其中也体现了数形结合、等价转化等重要思想的应用.