基于指令滤波的机械臂有限时间输出约束阻抗控制
2021-08-13李刚于金鹏刘加朋于海生
李刚,于金鹏,刘加朋,于海生
(青岛大学 自动化学院,青岛 山东 266071)
0 引言
近年来,机械臂技术的应用愈发普及,其结构越发繁杂化、精密化。因此为确保该技术的安全性和合规性,迫切需要更高精度的力/位控制方法。机械臂力/位控制已经成为现今重要的科研方向。在这一领域,众多学者作了大量研究,并给出多种控制方法,例如力/位混合控制[1]、阻抗控制[2]等。其中阻抗控制作为解决力/位控制问题的重要方法,具有抗干扰能力强、计算量相对较少以及易于机械臂进行力控制等优点[3],受到广泛关注。
运用于机械臂的阻抗控制技术发展迅速,HOGAN N首先提出了阻抗控制器的设计方法[4],使用阻抗控制理论来调节机器人末端执行器与环境作用力之间的相互作用,但并未实现对力的精度控制。乔兵等通过在机械臂中添加力传感器测得反馈力信号加以分析并与阻抗控制技术结合[5],成功提高了对机械臂末端与未知环境表面接触时接触力的控制精度;姜力等通过在阻抗控制的基础上加入模糊自适应控制技术,实现了在控制过程中通过模糊自适应技术[6]持续调整阻抗参数,测试可实现最优控制的阻抗参数以产生更优秀的控制表现,并将滑模位置控制作为内环,提高了系统的鲁棒性[7];LI P等提出利用模糊自适应技术逼近未知的机械臂系统模型参数,并进行阻抗控制器的设计,此技术可以取得较好的力/位控制效果[8],但在某些实际应用中,必须实现快速跟踪控制,上述方法往往不能满足条件。
为解决此问题,XUE C Q等将有限时间控制技术加入模糊自适应阻抗控制中,使机械臂系统在有限时间内系统输出信号趋于期望信号,在加快响应速度的同时极大地提升了系统的动态性能[9]。有限时间控制方法具有整定时间短、抗干扰能力强等优点,在实际应用中得到广泛应用。与非有限时间控制器相比,运用了有限时间控制技术的控制器能实现更优秀的鲁棒性和抗干扰性[10]。但是机械臂在未知或复杂环境中运行时,必须保证机械臂输出状态都限制在给定的有界区间内,否则有可能使机械臂受损,文献[9]所提出的机械臂控制方法并不能保证机械臂工作过程中的输出约束在有限区间内。
上述方法均采用反步法进行控制器设计,但在使用反步法设计控制器的过程中,虚拟控制律的反复求导提高了计算复杂性。为解决这个问题,本文引入了指令滤波误差补偿技术[11],该技术通过补偿信号解决滤波误差问题,并降低控制器设计的复杂性。基于以上问题,本文将障碍 Lyapunov函数[12-15]以及有限时间控制方法与阻抗控制方法结合,提出了应用于机械臂的有限时间输出约束模糊自适应阻抗控制。
最后,由仿真结果证明了本文所设计的机械臂系统控制器的可行性及有效性。
1 机械臂数学模型及初步变换
机械臂动力学方程[15]如下:
(1)
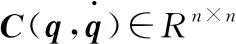
机械臂的运动学方程[16]如下:
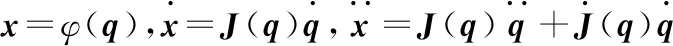
通过以上关系式转换,可得
(2)
其中:x∈Rm×1是笛卡儿坐标系中机械臂末端的坐标,m是机械臂运动空间的维度;q∈Rn×1是机械臂各关节的角度。
机械臂末端位置与末端力的阻抗控制关系式[17]
(3)
其中:E=xd-x,xd是命令轨迹;Md是机械臂期望惯性矩阵;Bd是机械臂期望阻尼矩阵;Kd是机械臂期望刚性矩阵。当机械臂末端在自由空间中运动时,Fe=0。
如果x精确地跟踪期望轨迹xr∈Rm×1,式(3)可以被写成下式
(4)
由式(4)中可以得知,若xd、Md、Bd、Kd已知,则可通过式(4)求出期望轨迹xr。
将式(2)带入式(1)可得
(5)
式中:
为了方便表示,重新定义新的变量为:
(6)
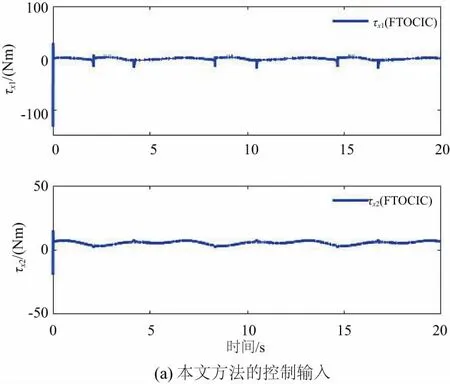
当机械臂在未知受限空间中工作时,机械臂的输出状态都应被限制在紧集Ωx内,其中Ωx={|x1i|≤kci,i=1,…,m},kci为正常数。控制目标是设计控制率τx使x1跟踪期望轨迹xr,同时,使机械臂控制系统的输出状态始终在给定的紧集Ωx中。
引理1[18-19]对于任意实数λ1>0,λ2>0以及0<γ<1,则有限时间稳定的扩展Lyapunov条件为
当满足上式时,系统半全局有限时间状态是稳定的。系统的收敛时间Ts可估计为
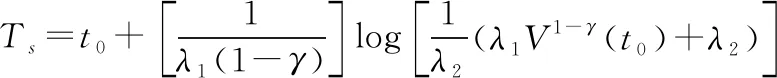
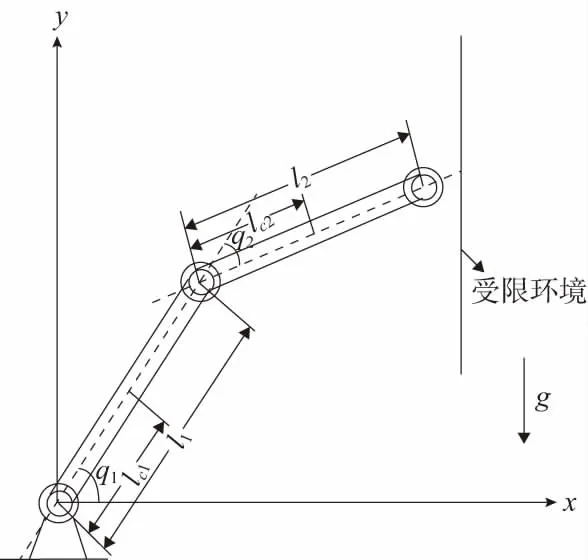
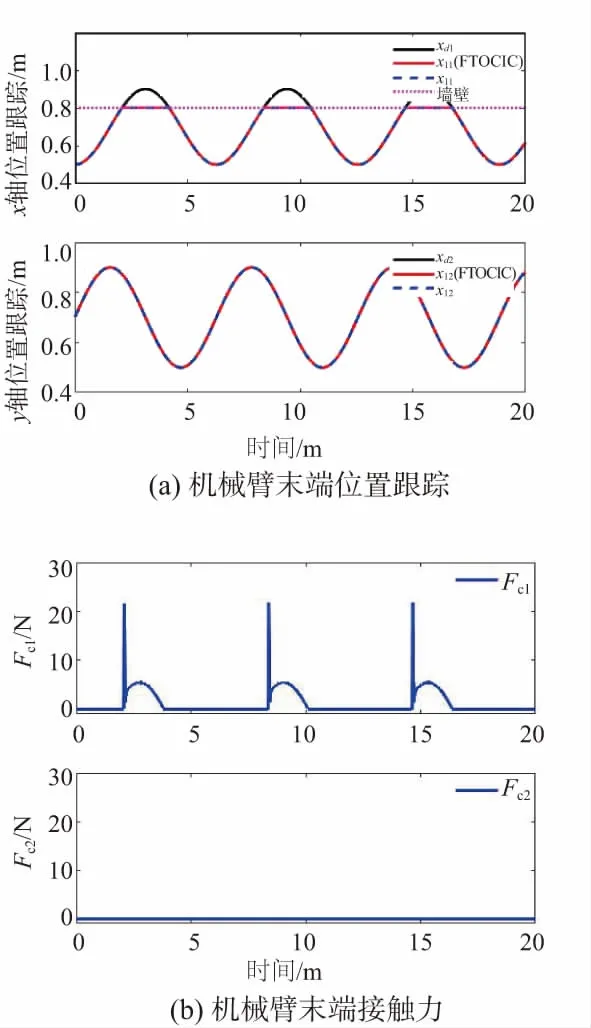
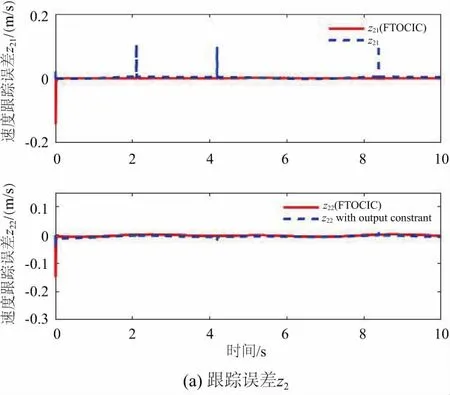
引理2[20]对于xi∈R,i=1,2,…,n,0 引理3[11]有限时间指令滤波形式为: 根据反步法原理定义误差变量如下: z1=x1-xr,z2=x2-x1,c。 其中:xr为期望轨迹;x1,c为指令滤波器的输出信号。定义滤波误差补偿信号为ξi=zi-vi,i=1,2。 步骤1:选择第一个子系统的障碍Lyapunov函数如下: (7) (8) 选取虚拟控制律α1和补偿信号ξ1, 即 (9) (10) K1=diag[k11,…,k1m];H1=diag[h11,…,h1m]; L1=diag[l11,…,l1m]均为正定矩阵。 将式(9)、式(10)带入式(8)可得 (11) 步骤2:选取第二个子系统的Lyapunov函数如下: (12) 对V2求导可得 (13) (14) 其中l为一个>0的常数。 (15) (16) (17) Fe+Gx+Cxx2 (18) 由引理2可以得出 (19) 将式(15)-式(19)带入式(13),可得 (20) 由杨氏不等式可知 (21) (22) (23) 将式(21)-式(23)带入式(20),可得 (24) 综合上述两式,可得 (25) 以下结论已经被证明[14]: 当满足条件|v1i|≤kai,0<γ≤1时,下列不等式成立: (26) 将式(25)及式(26)代入式(24),可得 (27) 其中: 将式(27)改写为 (28) 由v1=z1-ξ1可知|z1i|≤|v1i|+|ξ1i|≤kai+ϑ。同理,因为z1=x1-xr,可知|x1|≤|z1|+|xr|≤kai+ϑ+Y0=kc1。根据以上分析,机械臂系统的输出状态变量x被约束于紧集Ωx内,保证了机械臂的有限时间输出约束。 为了验证本文控制方案的有效性,以图1所示的垂直平面上的二自由度机械臂作为实验对象,机械臂工作在受限空间中,在x=0.8处有一面墙壁。 图1 二自由度机械臂机械模型 使用MATLAB对本文所提出的控制方法进行仿真分析。将本文所提出的有限时间输出约束阻抗控制(FTOCIC)方法与未考虑有限时间控制和输出状态约束的模糊自适应指令滤波阻抗控制方法进行仿真比较, 由式(6)可知仿真实验的旋转关节二自由度机械臂系统模型为: 其中x1=[x1,1、x1,2]T,x1,1、x1,2分别表示二自由度机械臂末端在笛卡儿坐标系x、y轴上的位置。 D(q)= 其中:qi表示机械臂的第i关节角度;mi和li分别为机械臂的第i节连杆的质量和长度;lci为机械臂的第i-1关节到i节连杆质心的距离;Ii为关节i基于坐标轴穿过关节的质心的转动惯量(i=1,2)。 二自由度机械臂的参数见表1。机械臂初始参数为x1=[0.502,0.702]T,x2=[0,0]T,滤波补偿信号的初始值为ξ1=[0,0]T,ξ2=[0,0]T。 表1 二自由度机械臂参数 [sin(t)cos(t)+sin(t)+0.5,2sin(t)cos(t)+cos(t)+1]T。 选择t∈[0,20]。 对于二自由度机械臂模糊自适应指令滤波阻抗控制法,控制规律选取k1=20,k2=560,r=1,l=1,σ=0.1。 对于二自由度机械臂模糊自适应有限时间输出约束指令滤波阻抗控制法,控制参数选取K1=diag[20,20],H1=diag[0.1,0.1],H2=2,L1=diag[0.01,0.01],L2=2,K2=560,ka=[0.005,0.005]T,r=1,l=1,σ=0.1,γ=0.6,R1=20,R2=0.6。 该二自由度机械臂的期待阻抗参数为Md=2I,Bd=diag[20,20],Kd=diag[50,50],模糊逻辑系统选择模糊集为 Sj(z)=exp[(zj+s)/4] 其中:j=1,2,3,4;s=-3,-2,-1,0,1,2,3。 仿真结果如图2-图5所示。图2是本文提出的控制方法与对比控制方法机械臂末端位置跟踪曲线图以及外界环境对机械臂末端施加接触力曲线图。由图2可知本文所提控制方法可有效使机械臂末端跟踪期望轨迹。图3是本文提出控制方法与对比控制方法的跟踪误差比较图以及误差变量v1变化曲线比较图。由图3可知,本文所提控制方法有效地提高了系统的响应速度,减小位置跟踪误差,并且使误差变量v1始终位于给定有界区间内。图4为本文提出的控制方法与对比控制方法的机械臂末端速度跟踪误差比较图以及误差变量v2变化曲线比较图。图5为本文提出的控制方法与对比控制方法的真实控制律τx的曲线图。 图2 机械臂末端位置与接触力 图3 跟踪误差z1与误差变量v1 图4 跟踪误差z2与误差变量v2 图5 控制输入τx 针对机械臂系统在受限空间中的跟踪控制问题,本文提出的基于指令滤波的有限时间输出约束模糊自适应阻抗控制方法,实现了对期望轨迹的有效跟踪控制,并且使机械臂输出状态都限制在预定义的约束空间中,具有更快的响应速度和更小的跟踪误差。本文所提控制方法与现有控制方法相比,能实现更少的响应时间以及更好的跟踪效果,将机械臂输出约束于给定的有界区间之中,保证了机械臂运行过程中的安全性。仿真实验的结果对比验证了本文所提控制方法的有效性。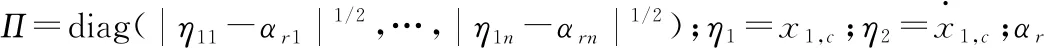
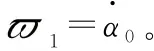
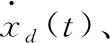

2 有限时间模糊自适应输出约束反步控制器设计
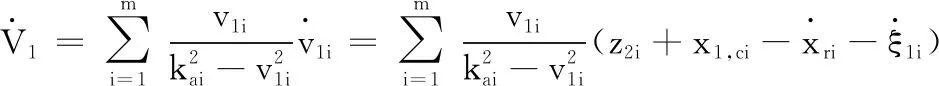
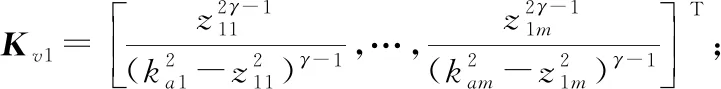
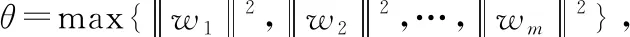
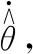

3 稳定性证明


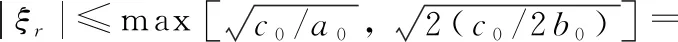
4 仿真结果分析


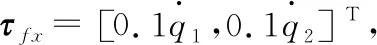

5 结语
