WWW型双输入行星减速器传动系统振动特性研究
2021-08-13张宽张庆
张宽,张庆
(南京理工大学 机械工程学院, 江苏 南京 210094)
0 引言
减速器作为航天航空飞行器伺服传动系统关键部件之一,其在工作时产生的振动会严重影响传动系统的精度以及减速器的寿命。沈稼耕等人研究了两组不同啮合相位的行星齿轮传动系统对人字齿行星齿轮传动系统振动特性的影响[1];刘凯文等人利用刚柔耦合模型对NGW型行星齿轮减速器传动系统进行振动特性分析[2]。本文利用理论法和有限元法分别计算行星齿轮传动系统固有频率,并与影响激励频率对比分析,验证了振动特性对减速器的重要性,为减速器避开共振频率提供参考依据。
1 WWW型双输入行星减速器的结构及工作原理
航天伺服双输入差速装置常选用结构简单的2K-H型轮系。圆柱齿轮2K-H型轮系按结构分类主要有NGW型、NW型、NN型、WW型。前3种结构都包含有内齿轮,而小尺寸硬齿面精密内齿轮加工困难,限制了这类行星轮系在高转速、高精度传动场合的应用。WW型轮系都是由外啮合齿轮组成,小模数外齿轮可磨齿加工,获得较高精度的硬齿面齿轮,但WW型差速轮系是正号机构,传动效率低,传动比大时甚至发生自锁,不适合用做动力传动。因此在WW型差速轮系的基础上构建新型WWW型的外啮合圆柱齿轮差动轮系,既便于磨齿加工获得高精度,又具有高的传动效率,适用于动力传动。
利用CAXA软件绘制WWW型双输入行星减速器的机构及装配简图如图1所示。减速器由1个WWW型2K-H负号差动轮系和1个定轴轮系组合而成。齿轮轴1和齿轮轴6为两输入轴,齿轮1和齿轮2 为太阳轮,齿轮3、齿轮4为行星轮,行星架H为输出轴。齿轮2、齿轮5、齿轮6组成定轴齿轮传动。齿轮1、齿轮4、齿轮3、齿轮2和行星架H组成两自由度的行星齿轮传动,该行星齿轮传动均为外啮合。正常工作时,由齿轮轴1和齿轮轴6同时输入动力源,转换后传动比为2.5;当电机1故障时,齿轮轴1制动,只有齿轮轴6作为输入源,转换传动比为5;电机2故障时同理可保证传动比为5。

图1 WWW型行星减速器的机构及装配简图


表1 各齿轮参数
利用三维建模软件CREO,建立各构件的三维模型并进行模型的虚拟装配,装配三维图如图2所示。
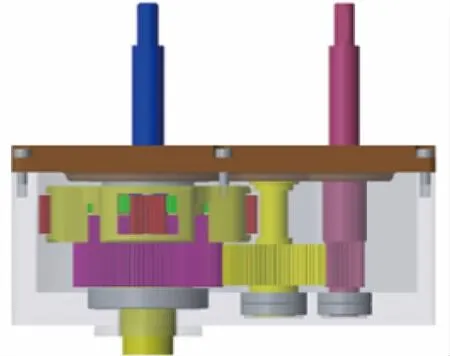
图2 三维装配模型
2 行星减速器传动系统数学建模
WWW型双输入行星减速器的齿轮传动系统由差动轮系和定轴轮系两部分组成。定轴轮系中齿轮转动时轴线位置固定,适宜采用固定坐标系建立振动数学模型。差动轮系中行星齿轮在绕中心轮转动的同时还会绕自身中心轴线自转,齿轮在啮合传动时坐标系是变化的,所以行星齿轮3和齿轮4应该采用动坐标系建立振动数学模型。基于行星架建立差动轮系的动坐标系,并以行星齿轮的中心位置为动坐标原点可得差动轮系端面动力学模型示意图,如图3所示。

图3 差动轮系端面动力学模型示意图
如图3所示,首先选择行星架、中心轮1和中心轮2共同的回转中心O为原点,建立它们各自的动坐标系,分别表示为{xH,yH,zH}、{x1,y1,z1}、{x2,y2,z2};各坐标系均以ωH的角速度随行星架和中心轮中心转动;接着以行星轮回转中心为动坐标系中心建立两组行星轮的动坐标系,行星齿轮3的动坐标系为{xpi,ypi,zpi},其中i=1,2,3,4;行星齿轮4的动坐标系为{xqi,yqi,zqi},其中i=1,2,3,4,两组行星齿轮的动坐标系均以ωH的角速度随行星架转动。因为第i个行星轮中心与行星架中心的连线和行星架动坐标系沿xH轴的夹角为Φi,Φi=2π(i-1)/4,所以行星齿轮3中动坐标系各轴方向可以进行定义,xpi轴沿夹角Φi正方向向外,ypi轴垂直于夹角方向并与行星架转向相同,zpi轴由行星轮中心垂直指向外,行星齿轮4坐标轴定义同理可得。对于定轴轮系,采用定坐标系为{xj,yj,zj},其中j=2,5,6,分别表示齿轮2、齿轮5和齿轮6。最后各构件沿横向振动的微位移用xn、yn表示,沿轴向振动的微位移用zn表示,扭转振动的微位移用un表示,其中n=1,2,…,5,6,H。
在对减速器传动系统模型进行动力学分析时,为了简化模型,方便计算,进行了以下假设:1)采用集中质量法,将啮合轮齿和轴承支撑简化为弹簧,将齿轮和行星架等构件视作集中刚体质量块;2)忽略齿侧间隙、综合误差和轮齿间的相互滑动及摩擦的影响;3)系统只需建立无阻尼自由振动方程,故忽略阻尼的影响;4)两组行星齿轮中每个齿轮的质量、结构、转动惯量和啮合刚度等完全一致。
2.1 传动系统相对位移分析
1)行星轮系弹性形变分析
假设中心轮指向行星轮的方向为啮合线正方向,根据图3中差动轮系端面动力学模型示意图进行齿轮端面啮合角、啮合刚度和支撑刚度的定义,αt14为中心轮1与行星轮4的端面啮合角,αt43为行星轮4与行星轮3的端面啮合角,αt23为中心轮2与行星轮3的端面啮合角;k14为中心轮1与行星轮4的啮合刚度,k43为行星轮4和行星轮3啮合刚度,k23为中心轮2与行星轮3的啮合刚度;k1、k2、k3、k4分别为中心轮和行星轮的支撑刚度。利用定义好的齿轮参数进行简单的数学计算可得各传动构件的弹性形变如下:
中心轮1相对行星轮4的位移沿啮合线方向投影为
δ1,qi=u1-uqi+x1sin(αt14-Φi)-xqisinαt14+
y1cos(αt14-Φi)-yqicosαt14;
中心轮2相对行星轮3的位移沿啮合线方向投影为
δ2,pi=u2-upi+x2sin(αt23-Φi)-xpisinαt23+
y2cos(αt23-Φi)-ypicosαt23;
行星轮3相对行星轮4的位移沿啮合线方向投影为
δqi,pi=uqi-upi+xqisinαt43-xpisinαt43+yqicosαt43-ypicosαt43;
行星架H相对行星轮3的相对位移和扭转位移在行星架坐标系上的投影为
行星架H相对行星轮4的相对位移和扭转位移在行星架坐标系上的投影为
2)定轴轮系弹性形变分析
图4为定轴传动部分端面动力学模型示意图。图中α25为齿轮2与齿轮5的啮合角,α56为齿轮5与齿轮6的啮合角;k25为齿轮2与齿轮5的啮合刚度,k56为齿轮5与齿轮6的啮合刚度;k2、k5、k6分别为齿轮2、齿轮5、齿轮6的支撑刚度。

图4 定轴轮系端面动力学模型示意图
齿轮5相对齿轮2的位移沿啮合线方向的投影为
δ5,2=u5-u2+x5sinα25-x2sinα25-y5cosα25+y2cosα25;
齿轮6相对齿轮5的位移沿啮合线方向的投影为
δ6,5=u6-u5+x6sinα56-x5sinα56+y6cosα56-y5cosα56。
2.2 传动系统动力学微分方程
定义齿轮1,2,…,6和行星架H的质量分别为m1,m2,…,m6,mH;齿轮1和齿轮6的基圆半径分别为rb1和rb6;在齿轮1和齿轮6上的输入转矩为T1、T6,行星架负载转矩为TH。将各传动构件的弹性形变代入牛顿第二运动定律,可得到各构件的动力学微分方程。
中心轮1的动力学微分方程为:
第i个行星轮4的动力学微分方程为:
第i个行星轮3的动力学微分方程为:
行星架H的动力学微分方程为:
中心轮2的动力学微分方程为:
齿轮5的动力学微分方程为:
齿轮6的动力学微分方程为:
3 行星减速器振动特性分析
3.1 齿轮传统系统啮合刚度和支撑刚度的确定
行星减速器工作时,传动系统齿轮啮合过程中啮合齿数是呈周期性变化的,轮齿承受载荷也是周期性变化的。所以啮合刚度也是随时间变化而周期性变化的,即啮合刚度是时变刚度。时变啮合刚度的计算方法主要有理论计算方法,如材料力学法和弹性力学法[3];数值计算方法如有限元法、边界元法和回归法,其中材料力学法应用较早也较广泛,典型方法有石川公式和威伯-班纳斯切克公式[4]。为了简化计算,本型行星减速器使用平均啮合刚度代替时变啮合刚度。平均啮合刚度表示1mm齿宽上的刚度,再将其转换成齿轮对啮合齿宽上的啮合刚度k,利用石川公式计算平均啮合刚度[5]。石川公式计算过程如下:
cγ=(0.75εα+0.25)c′
k=106·cγ·b
式中:εα为端面重合度;c′为单对齿啮合刚度;cγ为1mm齿宽上产生的平均啮合刚度,N·mm-1·μm-1;b为接触齿宽,k为接触齿宽上产生的平均啮合刚度,N/m,计算结果见表2。

表2 齿轮对啮合刚度
WWW型双输入行星减速器,所有轴承均为深沟球轴承。为了简化计算,根据文献和经验公式直接选取,取轴承径向支撑刚度为1×108N/m,轴向支撑刚度为1×107N/m。
3.2 传动系统固有振动特性分析
固有频率是系统的物理特性,与其所受到的外部载荷无关。在忽略传动系统的外部载荷与阻尼影响的情况下,建立WWW型行星齿轮传动系统的自由振动微分方程
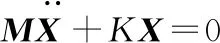
式中:M为传动系统的质量矩阵;X为传动系统的广义坐标列阵;K为传动系统的总刚度,包括啮合刚度和支撑刚度。
自由振动微分方程对应的特征值问题
式中:ωi和φi分别为第i阶固有圆频率和振型矢量,i=1,p1,…,6,H。
进一步得出系统第i阶固有频率为
fi=ωi/2π
代入传动系统齿轮基本参数,求出的质量矩阵和刚度矩阵为52阶矩阵,借助MATLAB软件编程对特征值求解,利用eig函数求出矩阵的全部特征值,程序如下(程序中略去了刚度矩阵和质量矩阵的输入):
E=eig(inv(M)*K);
E1=sqrt(E);
f1=E1./(2*pi);
[s,f2]=sort(T1);
运行程序可以得到的所有特征值,这些特征值即为传动系统各阶的固有频率。
由MATLAB软件的计算结果可得,WWW型行星齿轮减速器传动系统的最低固有频率为1 848Hz,所以只有当影响激励接近或者达到1 848Hz时,才会引起减速器传动系统共振。相关技术要求给减速器的最高转速为6 100r/min,通过最高旋转频率计算公式可得最高转速下的最高旋转频率为101.67Hz。
根据最高啮合频率计算公式,选定轴轮系可得最高转速下的最高啮合频率为2 440Hz。
最高旋转频率和最高啮合频率都远离理论方法计算的传动系统最低固有频率1 848Hz,所以不会引起减速器共振。通过分析传动系统的固有振动特性,可为减速器工作时避开共振频率提供依据。
4 基于有限元的减速器传动系统模态分析
有限元模态分析是通过有限元法计算得出结构部件特定的固有频率、阻尼比和模态振型的过程。其分析过程是将线性定常系统的自由振动解耦成N个正交的单自由度振动系统[6]。在利用经典的线性理论方法对齿轮传动系统进行固有频率求解时,理想化了一些诸如齿侧间隙、摩擦、阻尼影响以及齿轮啮合时刚度矩阵的时变问题等。然而借助有限元模态分析则可以方便地解出复杂系统的非线性模态。本文利用有限元软件ANSYS Workbench 对减速器齿轮传动系统进行有限元模态分析,计算出各阶固有频率和模态振型。
首先在Pro/E中建立齿轮传动系统的简化三维模型,然后将简化后的三维模型以stp格式导入到ANSYS Workbench中的Modal模块;接着定义材料属性:密度为7 800 kg/m3,弹性模量为207 GPa,泊松比为0.29,并按照程序对传动系统模型进行智能网格划分;然后定义约束:在各对啮合齿轮之间定义接触,接触类型为无摩擦Frictionless Support,在各转动件添加圆柱支撑Cylindrical Support,除行星轮约束轴向位移之外,其他转动件约束径向位移和轴向位移。最后求解出传动系统前6阶固有频率和模态振型。
传动系统的前6阶固有频率如表3所示。

表3 传动系统前6阶固有频率
传动系统的前6阶固有频率对应的模态振型如图5所示。

图5 传动系统前6阶模态振型图
基于有限元ANSYS Workbench计算出减速器齿轮传动系统的最低固有频率为1 865.1Hz,当影响激励接近或达到1 865.1Hz时传动系统会发生共振,造成齿轮损坏。已知输入最大转速6 100r/min,即减速器的最大旋转频率为101.67Hz,传动系统最大啮合频率为2 440Hz,都远离传动系统的最低固有频率,所以减速器传动系统不会发生共振。
5 结语
根据某航天飞行器的技术要求,设计出满足需求的高性能WWW型双输入行星减速器;利用理论计算方法和有限元模态分析法对减速器齿轮传动系统进行振动特性分析,结果验证了减速器影响激励不会引起传动系统的共振。
理论计算时,由于建立的齿轮传动系统模型忽略齿轮和行星架自身弹性变形,忽略阻尼和摩擦因素的影响以及简单化齿轮啮合刚度时变性等因素,因此理论计算的固有频率与减速器传动系统实际固有频率存在一定偏差。但理论计算出的固有频率已经远离了传动系统影响激励引发的频率。
基于有限元模态分析,能够准确有效地计算出非线性复杂系统的固有振动特性,相对于传统理论计算法更加准确,且有限元模态分析的固有频率结果与理论计算的结果接近,由此验证了利用理论法计算的齿轮传动系统动力学微分方程的正确性,同时为减速器避免共振提供了重要的参考数据。由于研究时间和资源有限,只对静态状况下减速器传动系统部分做了振动特性分析,对于减速器传动系统带有实际载荷及转速的预应力振动特性分析需要在今后工作中逐步完成。
