行星滚柱丝杠运动原理及有限元分析

王家健，张庆

(南京理工大学 机械工程学院，江苏 南京210094)

0 引言

标准式行星滚柱丝杠(下面简称行星滚柱丝杠)是将螺旋运动和行星运动结合在一起，将丝杠旋转运动转变为螺母直线运动的传动机构，具有承载能力强、刚度大、精度高、耐磨损、耐冲击和寿命长等特点，广泛应用于工业和国防军工领域[1]。

国内对行星滚柱丝杠的理论研究已经有一定的基础。靳谦忠和马尚君通过对行星滚柱丝杠的运动原理分析给出了相关参数的匹配设计条件[2-3]。在螺纹接触分析方面，许多学者基于赫兹接触理论和有限元方法进行研究，分析了螺距、牙型角、滚柱个数、载荷等因素对接触应力的影响，为提高行星滚柱丝杠的承载能力提供了参考[4-6]。但是目前对行星滚柱丝杠的有限元接触分析，都是将丝杠与滚柱、滚柱与螺母分开分析，而且只是分析一组或者几组螺纹接触对，没有对整体结构进行有限元分析。

1 行星滚柱丝杠运动原理分析

行星滚柱丝杠主要由丝杠、滚柱、螺母、内齿圈、保持架和弹性挡圈组成，结构形式如图1所示。

图1 行星滚柱丝杠结构形式

行星滚柱丝杠在工作时，丝杠通常作为动力输入端，只绕自身轴线转动；螺母通常与负载连接，只沿自身轴线移动；滚柱在螺母和丝杠之间做行星运动，并且与螺母相对轴向位移为零，与螺母一起沿轴向移动。行星滚柱丝杠运动简图如图2所示。

1—丝杠；2—保持架；3—滚柱；4—螺母。

图2中：dS、dR和dN分别为丝杠、滚柱和螺母的螺纹中径，由图1中几何关系有dN=dS+2dR；ωS、ωN、ωR和ωP为丝杠、螺母、滚柱和保持架的旋转角速度，ωN通常为0；pS、pR和pN分别为丝杠、滚柱和螺母的螺纹螺距；nS、nR和nN分别为丝杠、滚柱和螺母的螺纹头数，nR通常取1。

1.1 角速度分析

参照行星齿轮传动的分析方式[7]，给整体一个公共角速度，大小等于ωP，方向与保持架旋转方向相反，各构件的角速度变化如表1所示。

表1 角速度变化对比

根据表1，由传动比关系可得：

(1)

(2)

由式(1)、式(2)及dN=dS+2dR可得：

(3)

(4)

以上是假设滚柱与丝杠之间为无滑动的滚动，实际上滚柱与丝杠啮合可能存在滑动，所以ωR和ωP的实际数值要比理论值偏小。

1.2 螺纹旋向和头数分析

通常螺纹啮合需要保证螺距相等，即pS=pR=pN=p。螺旋副在旋转啮合过程中螺旋曲面的变化可以等效为其沿轴线的平移，移动方向可以通过左右手法则判断[8]。

1)滚柱和螺母螺纹旋向和头数分析

(5)

因为滚柱与螺母相对位移必须为0，所以式(5)中应取“-”，即滚柱与螺母螺纹旋向相同。由式(3)、式(4)、式(5)及LRN=0可得

nN=dS/dR+2

(6)

2)滚柱和丝杠螺纹旋向和头数分析

与滚柱和螺母的相对位移分析方法相同，滚柱和丝杠的相对位移LRS可以表示为

(7)

其中“+”号表示丝杠与滚柱旋向相同，“-”号表示丝杠与滚柱旋向相反。由式(3)、式(4)、式(7)可得

(8)

nS=dS/dR+2

(9)

滚柱和螺母相对丝杠的位移可以表示成

(10)

1.3 滚柱齿轮与内齿圈传动分析

1)因为齿轮传动为非承载部分，所以通常采用直齿圆柱齿轮啮合。设滚柱端齿轮和内齿圈齿数分别为zR和zN，模数为m。齿圈与螺母固连在一起，要满足滚柱与螺母纯滚动，则齿轮传动比与螺纹传动比相等，即

zN/zR=dN/dR

(11)

2)因为滚柱端齿与丝杠也要啮合，为了防止齿顶圆与丝杠螺纹牙底干涉，滚柱端齿齿顶圆直径不能大于滚柱螺纹大径dRa[2]，即

(12)

3)齿轮啮合传动必须要满足最小齿数要求，避免根切，即

(13)

当调整齿数和模数无法满足最小齿数要求时，可以采用变位齿轮设计或者改用短齿制，必要时可以采用非标准压力角齿轮设计[2]。

2 行星滚柱丝杠有限元建模

根据技术指标要求，结合上一节中运动分析结果，进行行星滚柱丝杠的结构设计；然后建立行星滚柱丝杠的三维建模；再把模型导入到ANSYS Workbench软件中，进行有限元建模[9]。

行星滚柱丝杠主要螺纹零件的主要参数如表2所示，齿轮零件的主要参数如表3所示。

表2 螺纹零件参数

表3 齿轮零件参数

2.1 三维模型简化

对模型进行简化，去除挡圈等零件以及零件的倒角和孔等特征，丝杠只截取啮合部分；行星滚柱丝杠为对称结构，滚柱个数为10且均匀布置，所以取模型的1/10进行研究。螺母上承受的轴向载荷为150kN，所以简化后的模型承受的轴向载荷为15kN；将简化后的三维模型导入到ANSYS Workbench中，如图3所示。

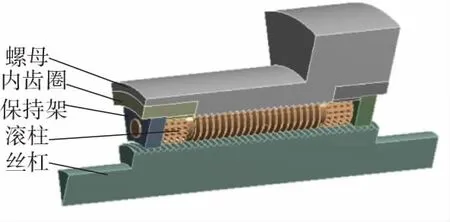
图3 有限元简化模型

2.2 材料分配及网格划分

对导入的模型进行材料分配，材料选用淬硬的轴承钢GCr15，其耐磨性好、硬度高，适合行星滚柱丝杠高承载、高刚度的要求。弹性模量E=200GPa，泊松比ν=0.3，屈服极限σS=1 667～1 814MPa。材料分配后对模型进行网格划分，如图4所示。

图4 有限元网格模型

2.3 接触设置

丝杠螺纹与滚柱螺纹、滚柱螺纹与螺母螺纹、滚柱端齿与内齿圈，这3处接触采用Frictional接触类型，可以法向分离和切向滑动。当切向分力大于最大静摩擦力时发生切向滑移，这样更符合行星滚柱丝杠的实际运动情况。

内齿圈与螺母之间为Bonded接触类型，法向和切向均无相对位移。

保持架只对滚柱起导向作用，不是承载及定位的零件，所以滚柱与保持架、保持架与内齿圈之间为Frictionless接触类型，法向和径向都可以有小位移。

2.4 边界条件设置

螺母只沿自身轴向平移，采用Displacement约束，只保留轴向移动自由度；对螺母法兰面施加15kN的轴向载荷。

滚柱即做行星运动又沿轴线平移，采用Cylindrical Support约束，保留旋转和轴向平移自由度。保持架同样既有旋转运动又有轴向移动，也采用Cylindrical Support约束，保留旋转和轴向平移自由度。

丝杠一端固定一端支承，所以固定端采用Fixed Support约束，完全限制6个自由度，支撑端采用Displacement约束，只保留轴向移动自由度。

因为模型只有1/10，所以对丝杠、保持架、内齿圈和螺母的剖面施加Frictionless Support约束，即法向无变形，其他方向可以自由变形。

3 行星滚柱丝杠有限元求解结果分析

3.1 有限元求解结果

图5和图6分别给出了螺母和滚柱螺纹接触点以及丝杠和滚柱接触点的等效应力云图。从图5中可以看出，螺母和滚柱螺纹接触点最大应力在滚柱螺纹牙上，为1 499.5MPa；从图6中可以看出，丝杠和滚柱螺纹接触点最大应力在丝杠螺纹牙上，为1 491.4MPa。

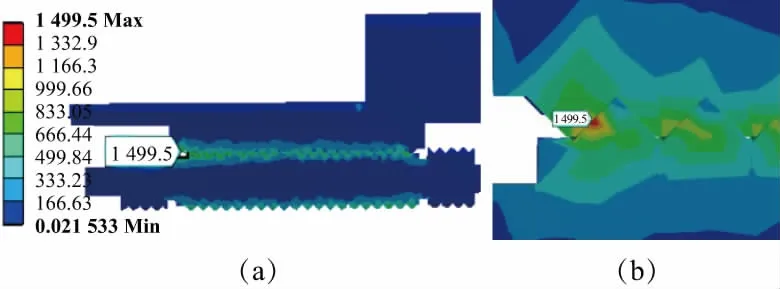
图5 丝杠与滚柱接触点等效应力云图

图6 螺母与滚柱接触点等效应力云图

丝杠、滚柱和螺母螺纹的接触应力都小于屈服极限，满足强度要求。但是螺纹牙存在载荷分布不均的情况，如图7所示，螺母左端第一个螺纹牙的等效应力最大，然后往右呈现减小的趋势。滚柱和丝杠螺纹牙的应力情况与螺母类似。

图7 螺母螺纹等效应力云图

3.2 牙型角对接触应力的影响

为了研究牙型角对螺纹接触应力的影响，不改变螺纹的其他参数，在螺距为2mm时，分别对牙型角为60°、70°、80°、90°、100°时进行有限元仿真求解，有限元求解结果如表4所示。

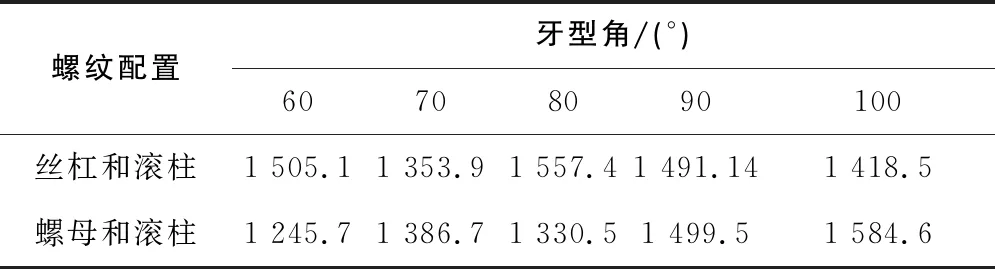
表4 不同牙型角的螺纹最大接触应力对比 单位：MPa

从表4可以看出牙型角在70°时螺纹接触应力最小，其次是90°，而在60°、80°和100°时，最大接触应力都超过了1 500MPa。根据文献[10]，牙型角与行星滚柱丝杠的传动效率有着紧密的联系，牙型角越大传动效率越高，所以综合考虑传动效率和螺纹接触强度，通常选择牙型角为90°。

3.3 螺距对螺纹接触应力的影响

为了研究螺距对螺纹接触应力的影响，不改变螺纹的其他参数，在牙型角为90°时，分别对螺距p为1.5mm、2mm、2.5mm、3mm和3.5mm时进行有限元仿真求解，有限元求解结果如表5所示。

表5 不同螺距的螺纹接触应力对比 单位：MPa

从表5可以看出，随着螺距的增大，接触应力变化较大，而且接触应力有增大的趋势。因为螺纹总长度相同，当螺距越大时，相应的螺纹接触点越少，从而降低了行星滚柱丝杠的承载能力。

4 结语

1)通过类比行星齿轮传动的分析方法，对行星滚柱丝杠的运动原理分析，得出丝杠、滚柱和螺母的螺纹旋向相同，螺纹头数满足nS=nN=dS/dR+2。

2)对行星滚柱丝杠螺纹的接触应力进行有限元仿真分析，并且研究了螺纹的牙型角和螺距对接触应力的影响，牙型角通常选择90°，螺纹最大接触应力随螺距的增大而增大。