电力电子化电力系统多时间尺度建模与算法相关性研究进展

陈 垣，张 波，谢 帆，丘东元，陈艳峰

（华南理工大学电力学院，广东省广州市 510640）

0 引言

进入21世纪以来，电力电子装置在电力系统发电侧、输电侧及用电侧的渗透率逐年增加，电力系统呈现出电力电子化的趋势［1-3］。然而，电力电子装置固有的低惯性、快速性等特性，改变了以同步机为主导的传统电力系统惯性大、时间响应长的特征，为电力系统引入了新时间尺度。传统电力系统设备的长时间尺度与电力电子装置的短时间尺度之间发生耦合，导致了多时间尺度问题。

在电力电子化电力系统中，典型的多时间尺度问题包括电力电子装置的可靠性评估和电力电子化电力系统的稳定性分析。在电力电子装置的可靠性评估中，短时间尺度的器件机理模型用于研究器件击穿过程，模型准确但复杂；长时间尺度的经验模型用于研究器件老化过程，模型简单但不准确。因此，电力电子装置的可靠性评估，需要同时考虑短时间尺度上的击穿和长时间尺度上的老化，是典型的多时间尺度问题［4-5］。在电力电子化电力系统的稳定性分析中，长时间尺度的机电暂态模型适用于电路拓扑恒定的传统电力系统，分析计算简便。但是，机电暂态模型无法解释拓扑周期变化的电力电子装置引起的次同步振荡［6］、超同步振荡［7］、高频振荡［8］等现象。短时间尺度模型可以准确描述以上现象，但是结构复杂，在现有计算条件下，无法用于大规模系统建模。因此，电力电子化电力系统稳定性分析也是典型的多时间尺度问题。

以上多时间尺度问题需要通过多时间尺度模型来研究。电力电子化电力系统多时间尺度建模是一个新的课题，一是电力电子化电力系统的研究刚刚起步，建模还没有统一的方法；二是电力电子化引入了新的时间尺度，例如器件开关时间、电路时间尺度，因此，现有电力系统尺度模型不能准确描述其特性，必须建立涵盖电力电子的多时间尺度模型。根据所研究问题对计算精度的要求，综合运用相关领域知识建立或简化模型，从而简化模型分析、减少计算量、提高计算效率，使得模型在现有条件下可分析、可计算［9］。多时间尺度模型是电力电子化电力系统稳定性分析、控制等的基础。

多时间尺度模型与现有电力系统单时间尺度模型不同，一是体现在模型更准确和更全面，包含不同时间尺度模型；二是算法更复杂。若沿用传统的单时间尺度算法，采用短时间尺度模型的步长计算无法保证长时间尺度模型计算精度，存在收敛性和计算时间过长的问题；而采用长时间尺度模型的步长计算将无法准确描述短时间尺度模型特性。因此，多时间尺度建模过程不仅是一个建模问题，还是一个算法研究课题，多时间尺度建模过程必须考虑其算法。

虽然在电力电子和电力系统领域，多时间尺度建模研究才刚刚起步，但是在物理、化学等领域，多时间尺度建模已取得了一定进展，形成了一套系统理论，2013年诺贝尔化学奖就授予了“化学反应仿真中多尺度建模及算法研究”［10-12］。根据现有多尺度建模理论，在进行多时间尺度建模时，首先需要了解多时间尺度算法的基本原理及其适用范围，一种多时间尺度算法往往仅适用于具有相应性质的多时间尺度模型；然后，需要根据不同时间尺度模型之间的相关性，获得多时间尺度模型的性质；最后，需要综合考虑模型和算法的特点，为模型选择适用的算法，以实现模型和算法的配合。例如，在多时间尺度算法中，谐波平衡法适用于存在周期性的系统，对于周期变化的多时间尺度模型，可以选择谐波平衡法进行简化和求解，以实现模型和算法的配合。

本文的目的在于根据以上多时间尺度建模理念，分析电力电子化电力系统多时间尺度建模与算法的关系，系统地梳理电力电子化电力系统多时间尺度建模已取得的成果，提出电力电子化电力系统多时间尺度未来研究存在的问题并探讨解决思路，为得到电力电子化电力系统多时间尺度建模的系统理论提供参考。为此，本文基于多时间尺度分析理念，首先分析现有多时间尺度算法及其适用范围；进而基于相同数学形式模型可以采用相同算法计算的准则，将电力电子化电力系统划分为元器件机理、切换系统、电磁暂态、机电暂态4个时间尺度；然后，通过不同时间尺度模型之间的相关性，探讨多时间尺度模型的性质，阐明多时间尺度模型与算法的相互制约关系；最后提出电力电子化电力系统多时间尺度建模与算法待解决的问题及研究展望。

1 多时间尺度算法

多时间尺度算法实现了不同时间尺度模型之间的融合，是多时间尺度的核心。本章主要介绍了目前常用的多时间尺度算法，包括平均法、预计算法、渐进法、谐波平衡法和希尔伯特变换法。不同算法的适用范围不同，在实际应用中采用何种算法，应依据多尺度模型的仿真速度、精度和收敛性等确定。

1.1 平均法

平均法是最基本的多时间尺度算法［13-14］。假设多时间尺度模型的状态变量可以分为短时间尺度变量xS和长时间尺度变量xL，则根据变量时间尺度的不同可以将模型分为2个部分，如式（1）所示。

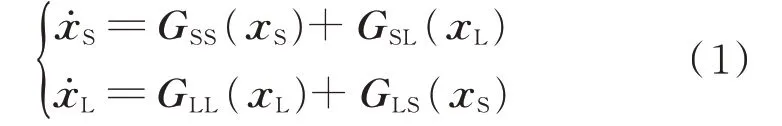
式中:GLL(xL)和GSS(xS)分别为长、短时间尺度变量受自身的影响；GSL(xL)和GLS(xS)分别为长、短时间尺度变量之间的耦合。

对于式（1）中的多时间尺度模型，目前主要通过步进式算法求解，这类算法的核心是由状态变量的当前值推算下一个时刻的值。在进行求解时，为了减少计算量，一般希望长时间尺度变量的时间步长ΔtL远大于短时间尺度变量的时间步长ΔtS，即

因此，多时间尺度模型求解中存在时间尺度不匹配的问题。以最基本的一阶欧拉法为例，在长时间尺度变量的一个时间步长ΔtL内，短时间尺度变量xS已经进行了M步计算，而长时间尺度变量xL却没有对应值用于计算。

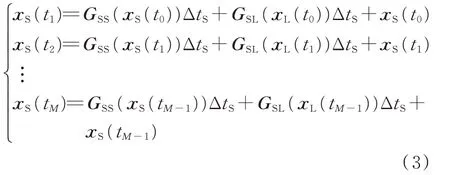
其中

式中:1≤δ≤M；t0为初始时刻。

同时，在计算长时间尺度变量时，短时间尺度变量有M个时刻的值对应，即

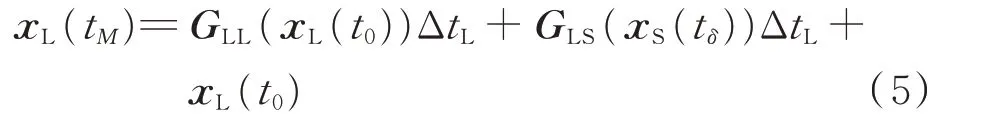
平均法是以上问题最基本的解决方法。它在计算长时间尺度变量时，使用短时间尺度变量M个时刻的平均值，即

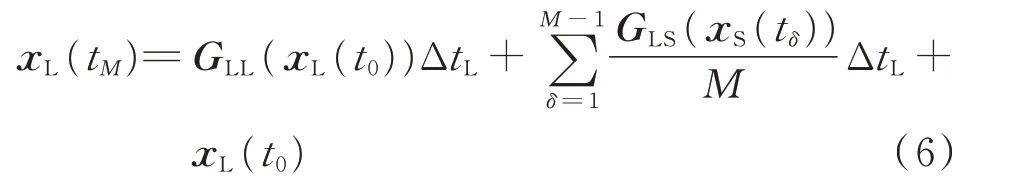
在计算短时间尺度变量时，使用长时间尺度变量的插值函数，即

平均法对多时间尺度模型的性质不作要求，因此在数值计算中得到了广泛应用。但是单独使用平均法仅能进行数值仿真研究，因此要进行解析分析还需要结合其他多时间尺度算法。

1.2 预计算法

预计算法是另一种多时间尺度数值算法［12，15］。对于式（1）的多时间尺度模型，如果短时间尺度变量的计算仅和长时间尺度变量xL中的少部分变量x͂L有关，则可以预先选择x͂L的不同取值，进行预计算。

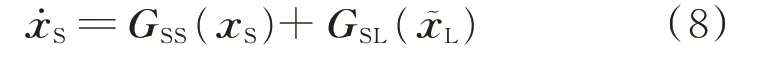
然后，将式（8）得到的xS代入耦合项GLS(xS)，得到耦合项和x͂L之间的对应关系H(x͂L)。

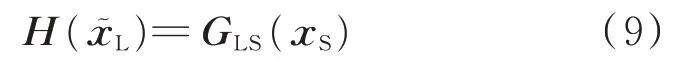
最后，将式（9）代入式（1），就可以消除短时间尺度变量，得到统一时间尺度模型。

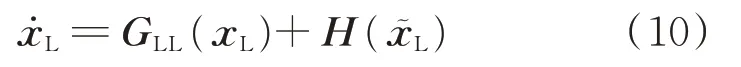
预计算法的效率取决于x͂L中包含的变量数量。当x͂L中变量数量增加时，预计算法的计算量呈指数增长。若x͂L中包含1个变量，计算量记作m，则在n个变量时，预计算法的计算量为mn。因此，预计算法仅适用于长、短时间尺度模型计算相对独立的情况。在多时间尺度建模和计算中，需要根据系统的性质来决定是否使用预计算法。

1.3 渐进法

在多时间尺度模型中，当长、短时间尺度模型的参数有明显差异时，可以使用渐进法［16-17］。渐进法的标准方程形式可以表示为:

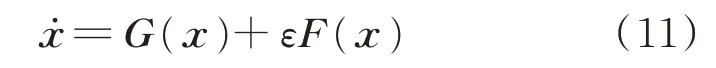
式中:G(x)和F(x)表示与变量x相关的一般通式；ε为表征长、短时间尺度模型参数差异的变量且ε≪1，例如，对于周期运行的电力电子装置，可以选择开关周期T作为ε。

根据式（11）所示的标准方程可构造渐进解，即

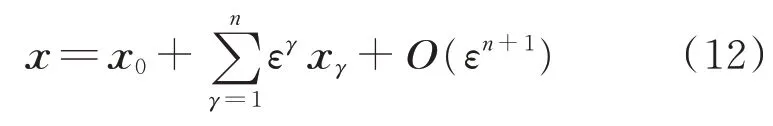
式 中:x0为x展 开 的0次 项；xγ为x展 开 的γ次 项；O(⋅)表示取同阶无穷小运算。

将渐进解代入式（11），忽略ε的n+1次项得到:

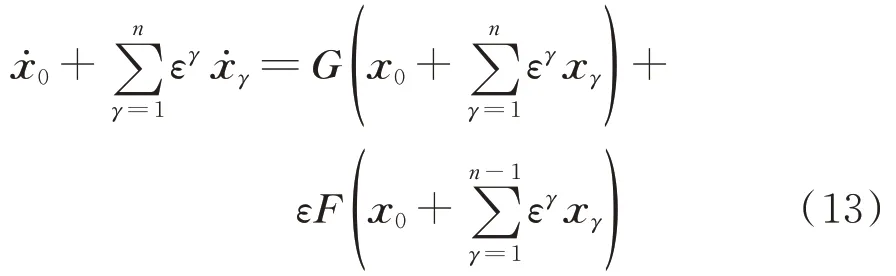
匹配ε的同次项，对于x0和xn可以得到:

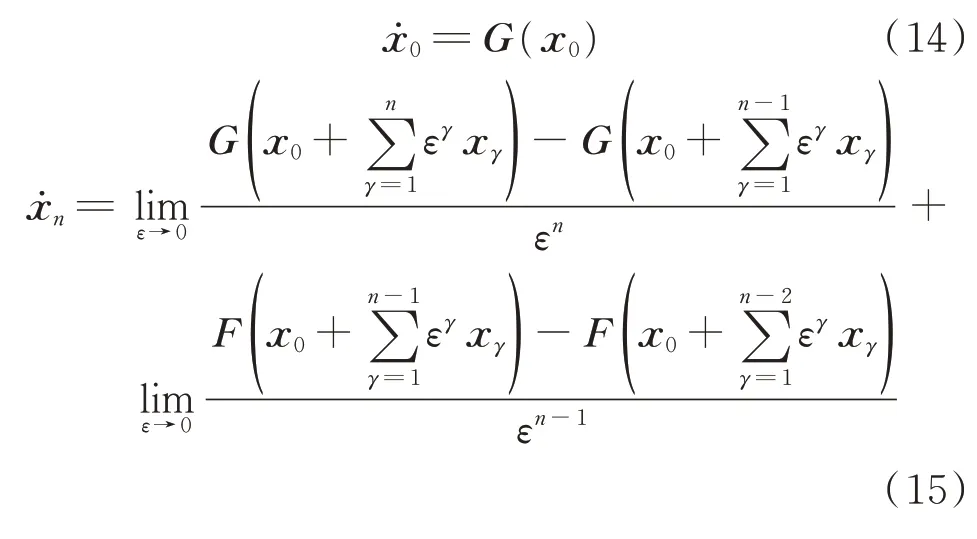
F（x）和G（x）为线性函数时，式（15）可简化为:

在 渐进法 处 理 后，计算xn只需要x0到xn−1，因此模型可以从x0到xn逐级求解。同时，各级模型均不含ε，为单一时间尺度模型。渐进法将单个多时间尺度问题转化为多个单时间尺度问题，简化了模型的分析和计算。

运用渐进法有2个前提:首先，模型可转化为式（11）的标准形式；其次，如式（12）所示，渐进解的收敛速度与ε有关，为减少模型展开阶数，长、短时间尺度模型的参数差异要足够明显，即ε要足够小。

1.4 谐波平衡法

周期变化的多时间尺度系统可以采用谐波平衡法进行分析［18-19］。一个典型的周期时变线性系统可以表示为:

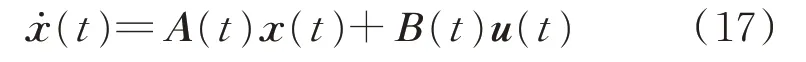
式中:A（t）和B（t）为周期为T的时变矩阵；x(t)和u(t)分别为状态向量和输入向量。

对式（17）中的x（t）、A（t）和B（t）进行傅里叶分解可得（为方便书写，本节以下式中省略了变量t）:

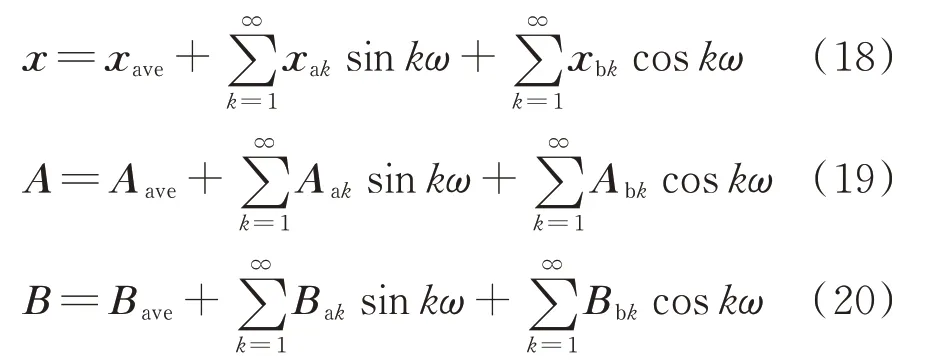
式中:xave、Aave、Bave为傅里叶展开的0次项；xak和xbk为傅里叶级数的第k次谐波系数；Aak、Abk、Bak、Bbk为傅里叶展开的第k次系数。

角频率ω满足式（21），即

将式（18）—式（20）代入式（17），并对三角函数的系数进行比较可以得到如式（22）—式（24）所示表达式。

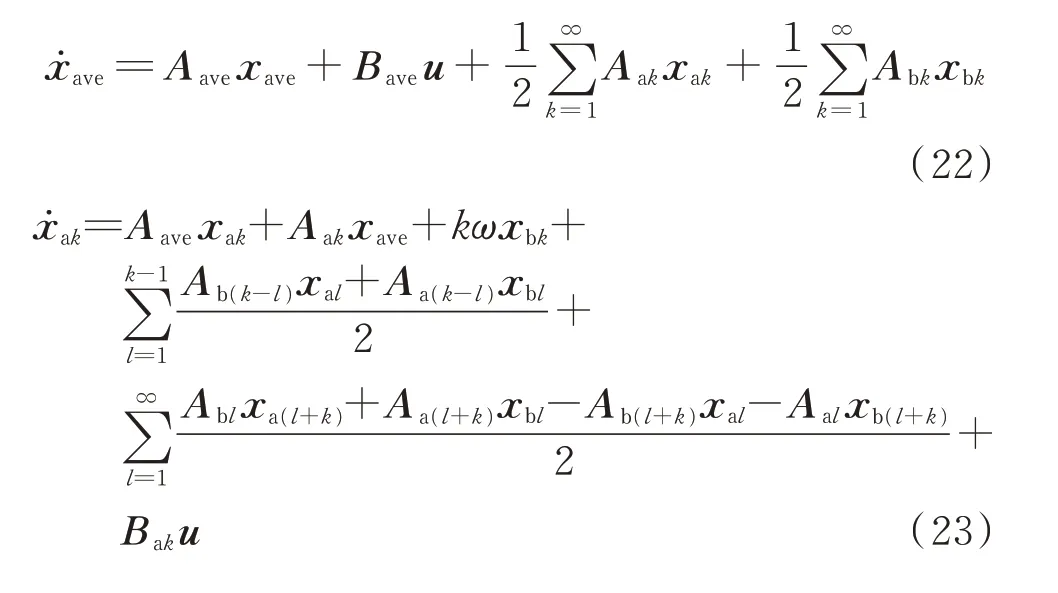
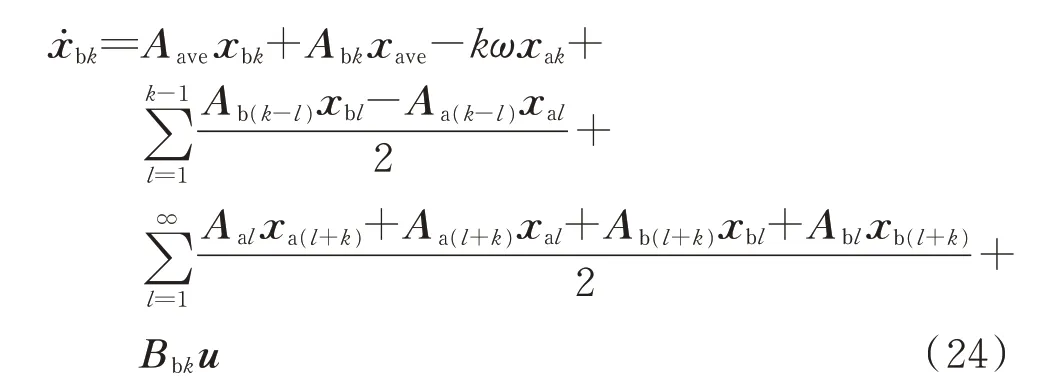
实际使用谐波平衡法时，只能选择式（18）—式（20）中的前N次谐波进行分析，因此存在截断误差。通过谐波平衡法，一个周期时变线性系统被转化为时不变系统，但状态变量数量增加到原先的2N+1倍。应用谐波平衡法时，需要权衡模型结构简化和状态变量数量增加对计算和分析的影响。

1.5 希尔伯特变换法

希尔伯特变换法原本是通信领域一种信号处理方法。近年来，该方法也开始用于电力系统多时间尺度仿真［20］。希尔伯特变换H(x(t))定义为原始信号x（t）和1/（πt）的卷积。

通过希尔伯特变换，信号正频率部分相位滞后π/2，负频率部分相位提前π/2，幅值保持不变。对式（17）中的状态向量x（t）和输入向量u（t）进行希尔伯特变换可以构造对应的解析函数z(t)和v(t)。

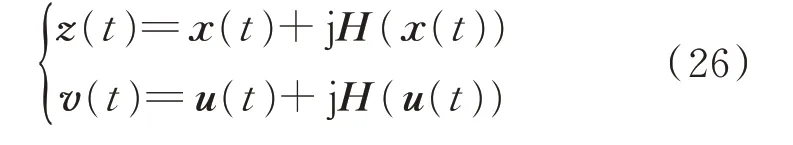
由于jH(x(t))相较于x（t），正频率部分相位相同，负频率部分相位相差π，因此，解析函数与原函数相比，正频率部分变为原来的2倍，负频率部分相互抵消。如果解析函数中所有频率分量集中在一个中心频率附近，则可以通过移频函数ejωt进行频率偏移，将状态变量转移到低频段，进而增加仿真步长，减少计算量。但是，当解析函数的频率分量较为分散时，不存在唯一的中心频率，在频率偏移后状态变量中依旧存在高频量，此时使用希尔伯特变换并不能减少计算量。

2 不同时间尺度电力电子化电力系统模型

2.1 时间尺度划分

清晰准确的时间尺度划分标准是多时间尺度建模的基础。传统的电力系统主要由旋转电机组成，可以通过机电和电磁过程时间常数的较大差异，准确区分电磁暂态和机电暂态2个尺度。然而，在电力电子化电力系统中，随着电力电子器件的引入，单纯以时间尺度进行划分，并不能得到清晰的结果。例如，大功率的晶闸管关断时间为数十微秒，而电力电子装置如逆变器的开关周期最小也为数十微秒，按照自然时间划分，两者应为相同时间尺度，但两者的模型和研究方法截然不同。时间尺度的划分标准应适应研究的需要，目前各研究领域主要针对不同模型进行研究，而非通过自然时间尺度划分。此外，现有多尺度算法在进行不同时间尺度的融合时，主要利用不同尺度模型的数学性质而非自然时间特性。因此，在划分时间尺度时，相比于自然时间尺度，以模型方程的数学形式为基准更利于开展多时间尺度研究，以及实现模型与算法的配合。

根据模型数学方程的形式不同，按照是否包含元器件机理模型、是否使用平均法以及是否使用相量法，电力电子化电力系统模型被划分为元器件机理、切换系统、电磁暂态和机电暂态4个时间尺度模型。其中，元器件机理尺度模型包含元器件机理模型，切换系统尺度模型不包含元器件机理模型但没有使用平均法和相量法，电磁暂态尺度模型在切换系统尺度模型的基础上通过平均法得到，机电暂态尺度模型在电磁暂态尺度模型的基础上通过相量法得到。采用该尺度划分标准具有以下3点优势。

1）各时间尺度模型都有明确的物理意义和数学特征。元器件机理尺度模型反映器件的工作机理，因而具有高度非线性。切换系统尺度模型反映电力电子装置切换运行的本质，模型结构随半导体器件的开关而变化。电磁暂态尺度模型反映电力电子装置的低频特性，模型结构不随时间发生改变。机电暂态尺度模型反映稳态下电力电子装置运行特性，稳态下的电力系统电压和电流按照正弦规律变化，因此可以使用相量描述。

2）不同时间尺度模型之间的关联性紧密。在元器件机理尺度模型中，可以用矩形波代替实际开关器件波形，得到切换系统尺度模型。在切换尺度模型中，当切换周期趋近0时，其状态矩阵和输入矩阵为各子模态状态矩阵和输入矩阵的加权平均，得到电磁暂态尺度模型。在电磁暂态尺度模型中，当电力系统处于稳态时，可以通过Park变换将静止坐标系下按照正弦形式变化的电压和电流瞬时值转变为dq0旋转坐标系下只包含直流分量的相量。

3）各时间尺度模型均有一定的研究基础，这有助于获得包含这些时间尺度的多时间尺度模型的性质。例如，当半导体器件和外电路参数确定时，半导体器件开关过程的电压和电流波形基本只受关断电压和导通电流的影响；在周期切换情况下，切换系统尺度模型的状态变量的纹波中仅包含切换频率整数倍的谐波成分。这些已知的模型性质是应用多时间尺度算法的基础。

2.2 元器件机理尺度模型

电力电子装置由电阻器、电感器、电容器、半导体器件等组成。如果在构建模型时按照装置内器件的工作机理建模，而非将器件视为理想器件，就可以得到电力电子装置的元器件机理尺度模型。在电力电子装置的所有器件中，半导体的工作机理复杂，对电力电子装置性能影响大，受到了较多关注。在半导体器件中，绝缘栅双极型晶体管（IGBT）器件由于可耐受电压高、电流承载能力强，广泛应用于电力电子装置中，IGBT工作机理模型也成为研究重点。

Hefner模型是经典的IGBT工作机理模型，由1个线 性 电 容Cgs，4个非线性 电 容Cgd、Cds、Ccer、Ceb，1个非线性电阻Rb和4个受控电流源Imos、Imult、Icss、Ibss组成的电路描述IGBT的工作机理［21-23］。如果用Hefner IGBT机理模型表示半桥型逆变器中的IGBT器件，就可以得到半桥型逆变器的元器件机理尺度模型，如图1所示。图中，除Hefner IGBT模型替换的IGBT器件外，Vdc为逆变器直流侧母线电压，D1和D2为IGBT器件反并联二极管，L为负载电感，RL为负载电阻。

图1 半桥型逆变器元器件机理尺度模型Fig.1 Mechanism scale model of half-bridge inverter components

2.3 切换系统尺度模型

在电力电子装置中，IGBT等半导体器件通常工作在截止区或饱和区。通过实验或者元器件机理尺度模型仿真，可以得到IGBT集射极电压vCE和器件电流iC的波形如图2中红色实线所示，包含开通、恒导通、关断和恒关断4个过程。其中，开通和关断过程的持续时间远小于恒导通和恒关断2个过程。

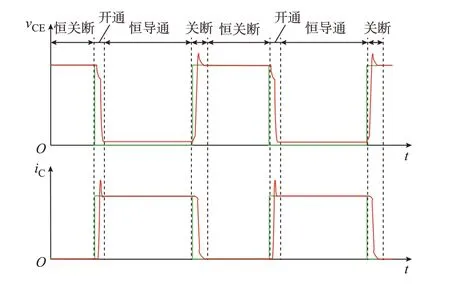
图2 IGBT及理想开关外特性Fig.2 External characteristic of IGBT and ideal switch

从开关器件外特性的角度来看，如果忽略开关过程、器件导通电压降和关断漏电流，则可以用图2中绿色实线代表的理想开关外特性取代实际IGBT器件的外特性。在恒导通阶段，器件两端电压为0，视为短路。在恒关断阶段，器件电流为0，视为断路。当器件处于不同状态时，电路的拓扑结构也会相应变化，这一现象可以通过切换系统模型来描述。切换系统是系统和控制学科的一个专用名词，它是一个由连续变量和离散事件组成的混合系统，电力电子变换器是一个典型的切换系统［24］。针对不同的拓扑结构分别列写状态空间方程，得到切换系统尺度模型［25-26］。

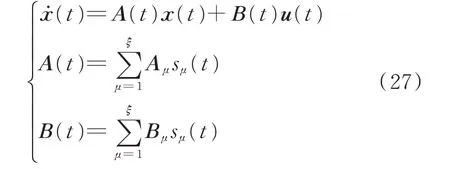
式中:Aμ为系统在模态μ下的状态矩阵；Bμ为系统在模态μ下的输入矩阵；sμ(t)为模态μ的开关函数，当系统处于模态μ时其取值为1，否则为0；ξ为系统的最大模态数。

2.4 电磁暂态尺度模型

对于运行在周期切换状态的电力电子装置，如果认为切换周期T趋于0，则式（27）表示的时变切换系统模型可以转变为时不变的电磁暂态尺度模型，分析和计算都相对简单［27-28］。用x*（t）表示电磁暂态尺度模型的状态变量，如式（28）所示。

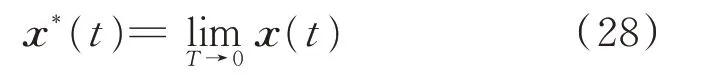
电磁暂态尺度模型可以表示为:

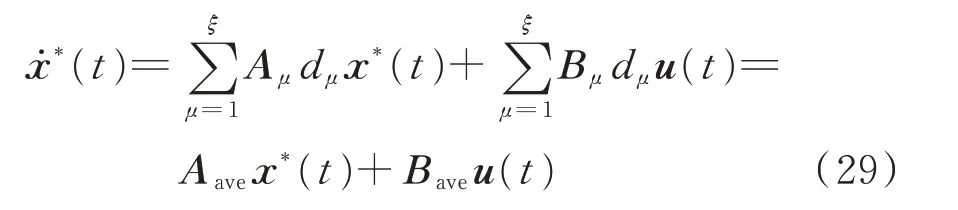
其中，状态矩阵Aave和输入矩阵Bave为各子模态状态矩阵Aμ和输入矩阵Bμ按照占空比dμ的加权平均。因此，该模型通常被称为状态空间平均模型［29］。

2.5 机电暂态尺度模型

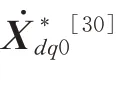
其中

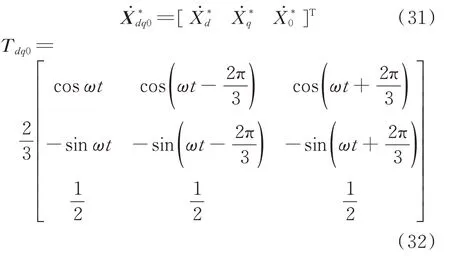
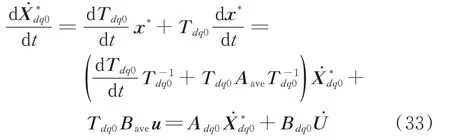
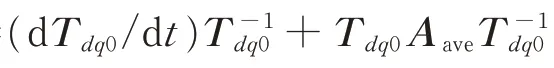
当电网电压和电流按照正弦规律变化时，Park变换后的模型中不含周期分量，相较于电磁暂态尺度模型的瞬时值，获得机电暂态尺度模型的相量的计算量更小。但是，当电力系统处于暂态时，由于三相状态变量不再按照正弦规律变化，Park变换并不能消除周期分量，使用机电暂态尺度模型也不能简化计算。

3 电力电子化电力系统多时间尺度模型

根据多时间尺度模型的性质，为模型选择合适的多时间尺度算法，实现模型中不同时间尺度的融合是多时间尺度建模的关键。本章主要介绍了目前常用的多时间尺度模型，按照时间尺度的不同，可以分为元器件机理-切换系统多时间尺度模型、切换系统-电磁暂态多时间尺度模型和电磁暂态-机电暂态多时间尺度模型3类。其中，元器件机理-切换系统多时间尺度模型主要采用预计算法处理，切换系统-电磁暂态多时间尺度模型主要通过渐进法和谐波平衡法处理，电磁暂态-机电暂态多时间尺度模型主要通过希尔伯特变换和平均法处理。

3.1 元器件机理-切换系统多时间尺度模型

如2.3节所述，元器件机理尺度模型和切换系统尺度模型仅通过开关器件的电压和电流相关联，其他变量之间没有直接关系，2个时间尺度模型的计算相对独立。因此，在处理元器件机理-切换系统多时间尺度模型时，可以使用预计算法得到实际开关器件的外特性，再代入切换系统尺度模型中。

针对半桥型逆变器，文献［31］提出了一种多时间尺度模型，如图3所示。图中:vS1和vS2为开关器件在开关过程中的电压；vSat1和vSat2为开关器件在导通时的电压降；iS1和iS2为开关器件的电流。在仿真过程中，该模型首先通过实验测量或者预计算法得到不同关断电压和导通电流下开关器件的外特性。然后，通过插值法为电压源和电流源赋值。最后，根据开关器件状态的变化，投入不同的电压源和电流源以模拟开关器件的实际外特性。

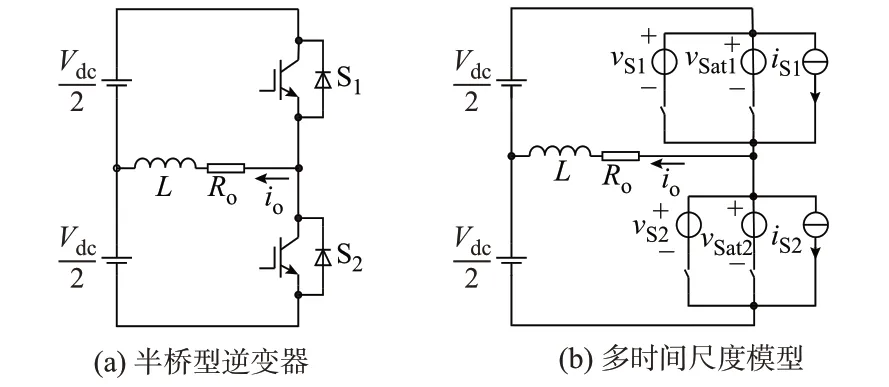
图3 半桥型逆变器及其多时间尺度模型Fig.3 Half-bridge inverter and its multi-time-scale model

在文献［31］所提出的多时间尺度模型的基础上，文献［32］进一步认为IGBT开关过程中的电压和电流波形可以使用折线替代，因此不需要获得所有时刻电压和电流的值，只需要获得折线的参数与关断电压和导通电流的关系即可。文献［33］则通过实验观察，近似得到了IGBT关断过程中电压和电流波形与关断电压和导通电流之间的解析表达式，比单纯的折线模型更加符合实际。

以上元器件机理-切换系统多时间尺度模型可以实现开关器件外特性的等效，比单纯的切换系统尺度模型更加精确。同时，模型中不直接包含元器件机理模型，结构较为简单。因此，这类多尺度模型逐渐被应用到电路仿真［34］和硬件在环仿真［35-36］等方面。

3.2 切换系统-电磁暂态多时间尺度模型

如2.4节所述，在开关周期T趋于0时，切换系统尺度模型转变为电磁暂态尺度模型。因此，可以通过渐进法将切换系统尺度模型（式（27））分为2个部分。

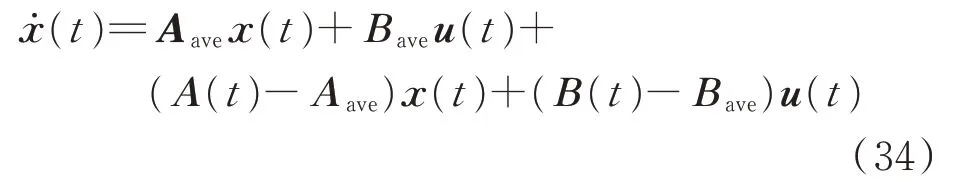
等号右侧前2项与电磁暂态尺度模型相同，对应渐进法标准方程式（11）中的G（x）；后2项在开关周期T趋于0时为0，对应渐进法标准方程式（11）中的εF（x）。

对状态向量进行渐进展开并保留前2项。

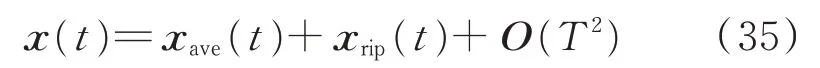
式中:xave（t）为状态向量中与开关周期T无关的分量；xrip（t）为状态向量中开关周期T的一阶向量。

将式（35）代入式（34）并按照开关周期T的次数进行比较可以得到基于渐进法的切换系统-电磁暂态多时间尺度模型［37-39］。

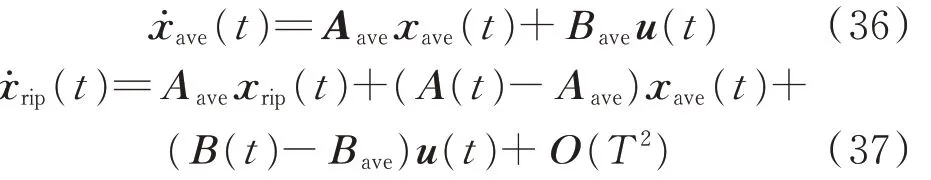
与原切换系统尺度模型相比，该多时间尺度模型方程中的状态矩阵均为时不变矩阵Aave，模型结构更加简单。同时，模型中用xrip（t）表示状态变量的纹波，计算结果比电磁暂态尺度模型更加精确。

除渐进法外，由于电力电子装置具有周期切换运行的性质，也可以通过谐波平衡法构造多时间尺度模型，该模型一般也被称为广义状态空间平均模型［40-41］或多频平均模型［42-43］。为简化分析过程，假设切换系统中仅包含2个模态，且切换系统尺度模型中的开关函数满足:

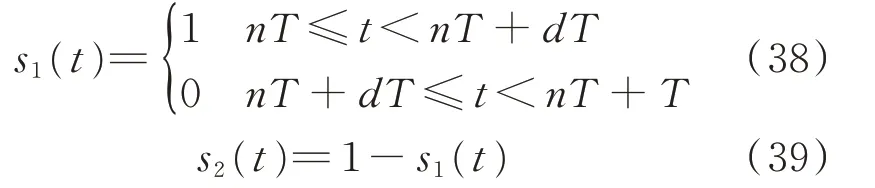
式中:d为占空比。

则开关函数s1（t）的傅里叶展开可以表示为:

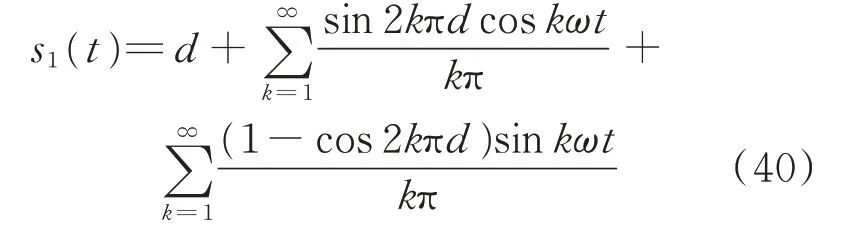
将式（40）代入式（27）可以得到式（19）和式（20）所示矩阵的傅里叶展开系数，即

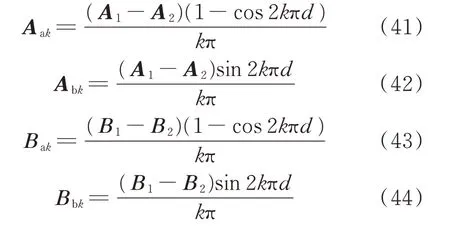
将式（41）—式（44）代回式（22）—式（24）可得基于谐波平衡法的多时间尺度模型。

在以上2种切换系统-电磁暂态多时间尺度模型中，渐进法和谐波平衡法分别使用三角波和正弦波来描述纹波。由于实际电力电子装置的状态变量波形更加接近三角波，基于渐进法的模型对纹波的描述更加准确。然而在平均值方面，基于谐波平衡法的模型对电磁暂态模型获得的平均值进行了修正，因此计算结果更加准确。目前这2种多时间尺度模型主要用于电力电子装置的稳定性分析和控制器设计［44-46］。

3.3 电磁暂态-机电暂态多时间尺度模型

如2.5节所述，当电力系统处于暂态时，其状态变量不再按照正弦规律变化，Park变换不再适用。然而，当暂态冲击未对电力系统的频率稳定产生明显影响时，电力系统中状态变量的频率分量依旧集中在电网频率附近，因此可以使用希尔伯特变换构造电磁暂态-机电暂态多时间尺度模型［47-48］。

假设电力系统的原始状态方程为:

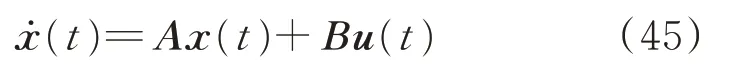
此时A和B为时不变矩阵。

将式（26）代入式（45）可以得到希尔伯特变换后的解析函数对应的状态方程为:

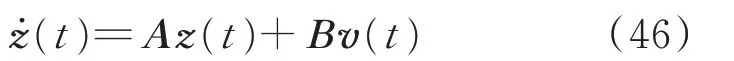
电力系统中变量的频率分量集中在电网频率附近，因此通过频率转移可以将变量转化为低频量。

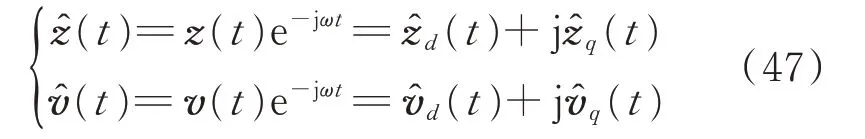
频率转移前后解析函数的导数满足:

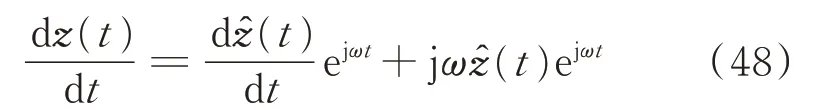
将式（48）代入式（46）可以得到电力系统的希尔伯特模型，即

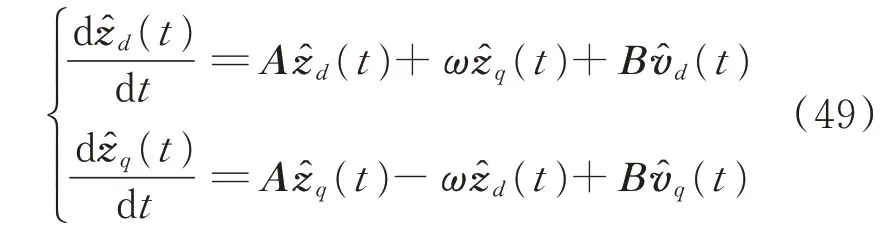
与原始的状态向量x（t）和输入向量u（t）相比，经过频率转移的解析函数ẑ(t)和v̂(t)中仅包含低频量，因此仿真计算时可以增大步长，加快运算。同时，希尔伯特变换法并不要求系统变量是正弦函数，因此可以分析非稳态电力系统。

在传统希尔伯特模型的基础上，文献［49-50］通过将希尔伯特变换的转移频率设定为一个独立变量，根据模型计算结果，自适应地调节转移频率进一步减少了模型计算量。文献［51-52］对系统中的变量进行经验模态分解，然后分别进行频率转移，所建立的模型更加适用于包含谐波的电力系统。文献［53］将谐波平衡法与希尔伯特变换法相结合，把系统的状态变量分解为傅里叶级数，然后针对不同频段的模型采用不同转移频率的希尔伯特变换进行处理，所建立的模型更加适用于包含模块化多电平变换器（MMC）等复杂电力电子装置的电力系统。

另一种电磁暂态-机电暂态多时间尺度模型则主要基于平均法［54-55］。在建模过程中，对电力电子装置采用电磁暂态尺度模型，按照小时间步长计算；对于同步发电机、输电线路等传统装备采用机电暂态尺度模型，按照大时间步长计算。然后，在不同时间尺度模型之间设置接口电路如图4所示。图中，等效电压源vL和阻抗ZL组成了机电暂态尺度模型的戴维南等效电路，等效电压源vS和阻抗ZS组成了电磁暂态尺度模型的戴维南等效电路。

图4 不同时间尺度模型接口电路Fig.4 Interface circuit of different time-scale models

当选择传输线作为机电暂态尺度模型和电磁暂态尺度模型的分界点时，戴维南等效电路中的阻抗ZL和ZS均为传输线的特征阻抗［55］，但等效电压源的值会随着模型中状态变量的变化而变化。当机电暂态尺度模型和电磁暂态尺度模型计算所采用的时间步长不同时，戴维南等效电路的参数更新也是不同步的，这一问题需要通过平均法解决。

在机电暂态尺度模型的一个长时间步长ΔtL内，电磁暂态尺度模型经过M个短时间步长ΔtS。因此，对机电暂态尺度模型而言，电磁暂态尺度模型的戴维南等效电路需要进行参数平均。

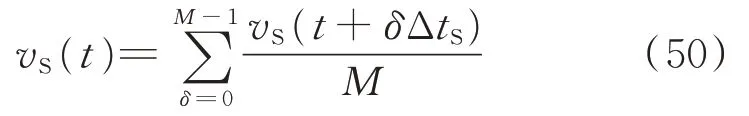
对电磁暂态尺度模型而言，机电暂态尺度模型的戴维南等效电路参数需要通过外插法计算。

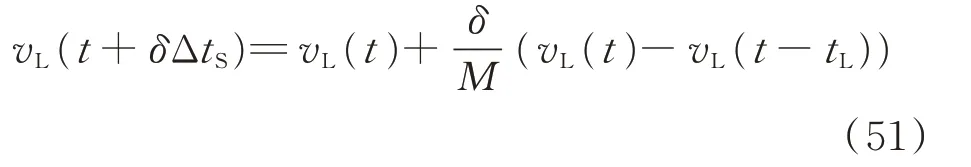
对于图4所示接口电路，除戴维南等效电路外，还可使用诺顿等效电路，两者之间没有本质区别。

以上2种电磁暂态-机电暂态多时间尺度模型除单独应用外，还可以组合使用，对传统电力系统部分通过希尔伯特变换建模，对电力电子装置部分通过平均法的接口电路处理。这进一步减少了多时间尺度模型的计算量，并解释了实际电力系统中出现的次同步谐振等现象［56］。

4 多时间尺度建模及算法待解决的问题及研究展望

虽然目前电力电子化电力系统的多时间尺度建模及算法已经取得了一定成果，但是依旧有待解决的问题。本章对这些问题进行了归纳，并对解决问题的途径进行了展望。

4.1 多时间尺度建模及算法待解决的问题

目前，多时间尺度建模的问题主要表现为缺少通用的多时间尺度模型。现有的多时间尺度模型仅能考虑2个相邻的时间尺度的相互影响，不一定能准确描述实际的电力电子化电力系统。例如，在分析电力电子化电力系统稳定性时，一般使用电磁暂态-机电暂态多时间尺度模型；对于电力电子装置使用电磁暂态尺度的状态空间平均模型，并不考虑电力电子装置的切换运行。然而，在开关频率较低时，电力电子装置的电磁暂态尺度模型和切换系统尺度模型的稳定性分析结果会有较大差异［57］。现有多时间尺度模型无法兼顾机电暂态、电磁暂态和切换系统3个时间尺度，无法评估这种模型误差对电力电子化电力系统的稳定性分析的影响。而缺乏通用的多时间尺度模型的根本原因，在于缺少通用的多时间尺度算法以及对多时间尺度模型的性质认识不足。

在多时间尺度算法方面，目前用于电力电子化电力系统的几种多时间尺度算法，除平均法之外，均对模型性质有特殊要求。预计算法要求短时间尺度变量的计算仅与少量长时间尺度变量有关；渐进法要求长、短时间尺度模型的参数有明显差异，且系统方程可以转化为标准形式；谐波平衡法仅适用于周期系统；希尔伯特变换则要求系统中状态变量的频率成分集中在一个中心频率附近。而平均法虽然对模型的性质不做要求，却只能用于数值计算，无法进行解析分析。以上多时间尺度算法的使用限制，导致一种算法仅能用于具有相同性质的模型中。然而，由于电力电子化电力系统的4个时间尺度模型的性质并不相同，现有多时间尺度算法并不通用，构建多时间尺度模型亟需一种通用的多时间尺度算法。

在多时间尺度模型性质方面，在电力电子化电力系统4个尺度的模型中，对切换系统尺度模型的性质已经有了一定的认识，相应的切换系统-电磁暂态多时间尺度模型也可以通过渐进法和谐波平衡法等多尺度解析算法进行分析。但是，对元器件机理-切换系统多时间尺度模型和电磁暂态-机电暂态多时间尺度模型的性质则存在认识不足的问题。在这2类多时间尺度模型中，电力电子器件工作机理的高度非线性和实际电力系统复杂的成分组成，阻碍了对模型的解析性质的认识。因此，目前对这2种多时间尺度模型，仅能通过多时间尺度数值算法计算，而不能通过多时间尺度解析算法分析。对于多时间尺度模型性质的认识不足限制了多时间尺度算法的应用。因此，电力电子化电力系统多时间尺度研究亟待加深对于多时间尺度模型性质的认识。

4.2 多时间尺度建模及算法研究展望

得到一个通用的多时间尺度模型，包含电力电子化电力系统的所有时间尺度，以分析各种因素对所研究问题的影响，将是电力电子化电力系统多时间尺度研究的最终目标。要实现这一目标，可以从以下3点入手。

1）针对多时间尺度算法问题，相较于多时间尺度算法研究，多空间尺度算法的研究更为成熟，因此可以借鉴多空间尺度算法，研究适合于电力电子化电力系统的多时间尺度算法。例如，将多分辨率分析法中的小波分析法应用到电力电子变换器的多时间尺度建模中［58］。

2）针对电力电子化电力系统多时间尺度建模问题，可以借鉴其他学科多时间尺度建模理论，如将物理、化学领域的Ginzburg-Landau相变模型［59］、Kohn-Sham方程［60］、多尺度复杂化学系统模型等成熟的多尺度模型［10］，推广到电力电子化电力系统中。

3）针对多时间尺度模型和算法相互依赖的问题，可以根据可计算理论，在现有计算条件下考虑模型的可计算性，确定多时间尺度建模方法，从而提出具有一般意义的多时间尺度模型和算法的耦合分析理论。

5 结语

电力电子化是电力系统未来的发展方向，然而电力电子装置的大规模应用，会导致传统电力系统的长时间尺度和电力电子装置的短时间尺度发生耦合，产生多时间尺度问题。为了准确描述多时间尺度特性，需要建立电力电子化电力系统多时间尺度模型。

本文基于多时间尺度分析理念，首先分析现有多时间尺度算法的基本原理及其适用范围；进而将电力电子化电力系统分为4个时间尺度；然后，通过不同时间尺度模型之间的关联性，探讨多时间尺度模型的性质，具体展示了多时间尺度模型与多时间尺度算法的相互制约关系；最后，提出电力电子化电力系统多时间尺度建模及算法待解决的问题及研究展望。本文得到以下结论。

1）电力电子化电力系统的多时间尺度分析与传统的单一时间尺度研究有根本的不同，不仅要建立多时间尺度模型，且建模过程必须要考虑计算方法，即模型和算法不能单独存在。

2）针对多时间尺度分析中模型与算法相配合的需要，电力电子化电力系统的时间尺度划分应以模型的数学形式为基准，而非以自然时间尺度为基准。具体而言，电力电子化电力系统可以划分为元器件机理、切换系统、电磁暂态、机电暂态4个时间尺度。

3）目前亟须提出通用的多时间尺度模型算法、加深对于多时间尺度模型性质的认识，以得到通用的多时间尺度模型。为解决以上问题，可以借鉴其他领域的多尺度研究成果，探索多空间尺度算法、可计算理论在电力电子化电力系统多时间尺度建模中的应用。