大学生高等数学“学习兴趣”“自我效能感”“学习焦虑”“学习动机”的关系研究

李 鹏，曹丽华

大学生高等数学“学习兴趣”“自我效能感”“学习焦虑”“学习动机”的关系研究

李 鹏，曹丽华

（深圳大学数学与统计学院，广东深圳 518060）

大学生高等数学学习动机的增强能够促进其学习的深度参与．厘清学习动机的影响因素及其路径，以在教学过程中针对性地应对，有助于提升高等数学教学效益．运用结构方程模型方法，对大学生进行调查后发现：高等数学学习兴趣对学习焦虑和自我效能感的影响，均达负向非常显著；学习兴趣对自我效能感的影响、高等数学自我效能感对学习动机的影响均达正向非常显著；在学习兴趣对学习动机的影响路径中，学习焦虑和自我效能感表现为完全中介效应．在高等数学教学过程中，应为学生提供探究机会，鼓励学生参加竞赛，关注学生个体进步，重视过程考核等．

学习动机；学习兴趣；自我效能感；学习焦虑；结构方程模型

1 问题提出

自我效能是指个体对其能否实施某一行为的能力的推测或判断，它主要通过个体经验、替代经验、言语劝说和情绪唤醒4个信息源形成．自我效能水平高低影响个体对任务的选择、付出的努力及在困难条件下对活动的坚持性[1]．作为需要付出一定努力的学习活动，是自我效能理论运用的沃土．学习自我效能感是指个体的学业能力信念，是学习者对自己能否利用所拥有的能力或技能去完成学习任务的自信程度的评价，是个体对控制自己学习行为和学习成绩能力的一种主观判断[2]．

数学自我效能感是国内教育心理学领域近二十余年的热点话题之一，但多集中于对中小学生数学自我效能感及其相关因素的探讨[3-5]，如数学学习兴趣显著影响数学自我效能感[6-7]．对大学生高等数学自我效能感的研究较为少见[8]，部分研究仅进行了经验性的总结[9]．为更全面地把握高等数学自我效能感及其作用机制，有必要从学习兴趣、动机、焦虑等非认知维度进行调研，获取真实结果，为有效改进高等数学教学，达成较好的教学效果提供支持．

高等数学是较为抽象的学科，对学习者思维的灵活性、深刻性和严密性均有着较高要求．随着高等教育“大众化”的逐步推进，高考录取率逐年攀升，多数从初等数学学习阶段就开始畏惧数学的大学生也必须学习高等数学．他们的普遍感受是高等数学难度大、听不懂，不容易通过考试．在课时量并不富余的情况下如何实现教学效益的显著改观，提高大学生高等数学学习的通过率和获得感，是任课教师面临的现实问题．提高教师教学水平，加强对大学生的督促管理是必要方法，但根本解决之道是重视如何引导大学生在高等数学学习过程中形成积极的情感态度体验．作为可以影响个体学习努力程度的高等数学学习自我效能感尤其值得关注．

学习兴趣是学生在学习活动中表现出的内在心向[10]，是非智力因素的主要成分之一[11]．作为学习兴趣的下位概念，数学学习兴趣的“心向”聚焦于数学，是学生进行数学学习活动的倾向，这种倾向依赖于学生对数学学习的价值认识、积极的情感体验、数学知识的积累以及主动学习数学的活动[12]．在高等数学学习阶段，学生的认知水平和情感体验更为成熟，知识积累更加丰富，学习活动也更多地依赖于自身的主动性．有研究表明[7]，数学学习兴趣对数学学业成绩有显著的直接影响，同时通过自我效能感对数学学业成绩产生显著的间接影响．类似研究结论表明，数学自我效能感和学习兴趣的相关性值得进一步探究，尤其是对需要更多自主性的高等数学学习而言．

基于已有研究对数学学习兴趣的维度划分[13]，高等数学学习阶段的个体兴趣所占的地位更加突出，维持的情境兴趣尤其是激发的情境兴趣可能由于教师教学工作量较大、师生互动缺失等原因，在实践中受到的重视程度不足，体现亦不够充分．

学习动机与学习兴趣有较强的相关性，有研究表明：学习兴趣层次高低制约学习动机水平[14]．学习动机可视作引起个体行为的内在原因，是引起、维持学生的学习活动，并导致学习活动趋向教师所设定目标的内在心理历程[10]．但动机指向的目标未必一定达成．倘能达成，或者说进行某种行为后获得了动机满足，则兴趣自然会产生并逐步得到强化．如学习者将成败归因于努力程度，后续的学习动机可能会得到巩固或增强；归因于自身不可控的试题难度或运气因素等，后续可能幻想“守株待兔”式的运气或采取“听天由命”式的放弃．自我效能感对于转化学习动机必然发挥作用，可以预测学习动机[15]，但这种作用是积极的还是消极的则是或然的．高等数学教学实践中期待的是自我效能感正向积极作用的发挥．

数学焦虑是个体在处理数字、使用数学概念、学习数学知识或参加数学考试时产生的生理变化和不安、紧张、畏惧等焦虑状态的情绪体验[16]，对学生的成绩有重要影响[17]．21世纪以来，数学学习焦虑的研究引起了学术界的关注，但相关研究尤其是较深入的实证研究主要集中于中小学阶段．如乡镇小学生的数学学习焦虑显著负向影响他们数学自我效能感[18]，数学学习兴趣是数学焦虑的主要成因之一[19]．由于学生认知能力的发展、学习经验的积累可能带来对数学焦虑主观理解的发展，将中小学阶段的研究结论直接迁移到大学生的高等数学学习亦有简单化之嫌．

自我效能感、学习动机、学习焦虑、学习兴趣在高等数学学习过程中的复合关系如何体现，相互影响的路径如何等问题需要进一步明确．研究者基于已有文献、调查数据分析、长期从事高等数学教学的经验和教学过程中与学生的交流互动，对其间的影响路径及程度进行了实证研究，以期为高等数学教学理论研究提供参考，为高等数学教学实践改革提供着力点．

2 研究对象与方法

2.1 研究对象

考虑研究对象需要具备较强的代表性，并需积累一定的高等数学学习经验，形成基本的认知结构，在主要的非认知维度也应较为稳定．因此选取已进行一学期高等数学学习的某地方院校2018级非数学专业本科生进行调查．调查采取立意抽样的方法，调查问卷采用现场发放、即时回收的形式进行，共发放问卷357份，剔除填写明显随意化（如均选择中间程度的选项），并以每一题项标准化后得到的值处于-3.25～3.25为标准，剔除不在前述范围的极端值情形，获得有效问卷340份，有效率为95.2%，其中男生174人（占比51.2%），女生166人（占比48.8%）．

2.2 研究工具

主要参考了吴红艳的数学学习兴趣量表[13]，章建跃的数学学习动机量表[20]，熊建华的数学焦虑量表[21]和边玉芳的自我效能感量表[2]．参考的量表均已在实践中进行过验证，具备较高的信度和效度．但由于原调查对象均为中小学生，基于调查对象的变化，在正式调查实施之前召开了由3位长期从事高等数学教学研究、实践工作的教师和3位数学教育专业的博士生参加的小型研讨会．参加者从不同专业视角、问题表述语意、问题同质性等方面对量表题项进行了初步删改，以更好地保障问卷的内容效度．高等数学学习兴趣量表、学习动机量表、学习焦虑量表和自我效能感量表各选取了8、4、11、8个题项．考虑到大学生的高等数学学习不同于中小学生的数学学习，家长、教师的督促作用要小得多，学习动机量表主要测量高等数学学习的内部动机（以下简称学习动机）；学习焦虑量表分为两个子维度，即应试焦虑和课堂学习焦虑．问卷均采用7点计分方式的Likert量表形式，其中学习兴趣、学习动机和自我效能感问卷的选项从“1非常不符合”到“7非常符合”；学习焦虑问卷的选项从“1没有焦虑”到“7非常焦虑”．得分越高表示被试在相应变量的认知或表现越强．

2.3 数据收集与处理

研究数据主要采用Mplus 8.0软件进行统计分析，主要运用了结构方程模型的分析方法，包括验证性因素分析、参数显著性估计、模型拟合度计算、信度和效度计算、回归分析和中介效应分析等．

2.4 研究假设和研究模型

基于对已有研究的回顾分析，研究者提出以下6个研究假设：

假设1 高等数学学习兴趣显著负向影响学习焦虑；

假设2 高等数学学习兴趣显著正向影响学习自我效能感；

假设3 高等数学学习兴趣显著正向影响学习动机；

假设4 高等数学学习焦虑显著负向影响学习动机；

假设5 高等数学学习自我效能感显著正向影响学习动机；

假设6 高等数学学习焦虑显著负向影响学习自我效能感．

基于以上6个假设，构建的研究模型如图1．

图1 高等数学学习结构模型

3 研究结果与分析

3.1 验证性因素分析

鉴于参考的量表较为成熟，加之经过专家的删改、加工，内容效度和题项鉴别力得到了一定保障．由于量表使用对象发生变化，对专家研讨后保留的问题仍进行了验证性因素分析，结果表明大部分题项鉴别力较强．对于各量表因素负荷量低于0.6的题项予以删除，学习兴趣、学习动机、自我效能感和学习焦虑4个维度各保留了6、3、6、10个题项（保留后的问卷见附录）；其中学习焦虑维度拆分成了应试焦虑和课堂学习焦虑（见表1）．

每一维度第一个题项的非标准化负荷量固定为1后，得到的各个题项的参数估计值均大于0，对应值均小于0.001，达到非常显著的水平．各维度的组合信度（Composite Reliability，CR）处于0.714～0.932之间，内部一致性达到较高水平[22]．平均方差萃取量（Average Variance Extracted，AVE）处于0.455～0.774之间，表示5个维度（学习焦虑的两个子维度独立计算了AVE）对各自包含的几个题项的平均解释能力较强或处于可接受范围，各维度的信度达到了可接受或较理想的水平，存在较明显的收敛效度[23]．作为对应标准化因素负荷量的平方，所有题项的多元相关平方（Square Multiple Correlations，SMC）值均大于0.36，大多数题项达到或接近0.5的理想值水平．

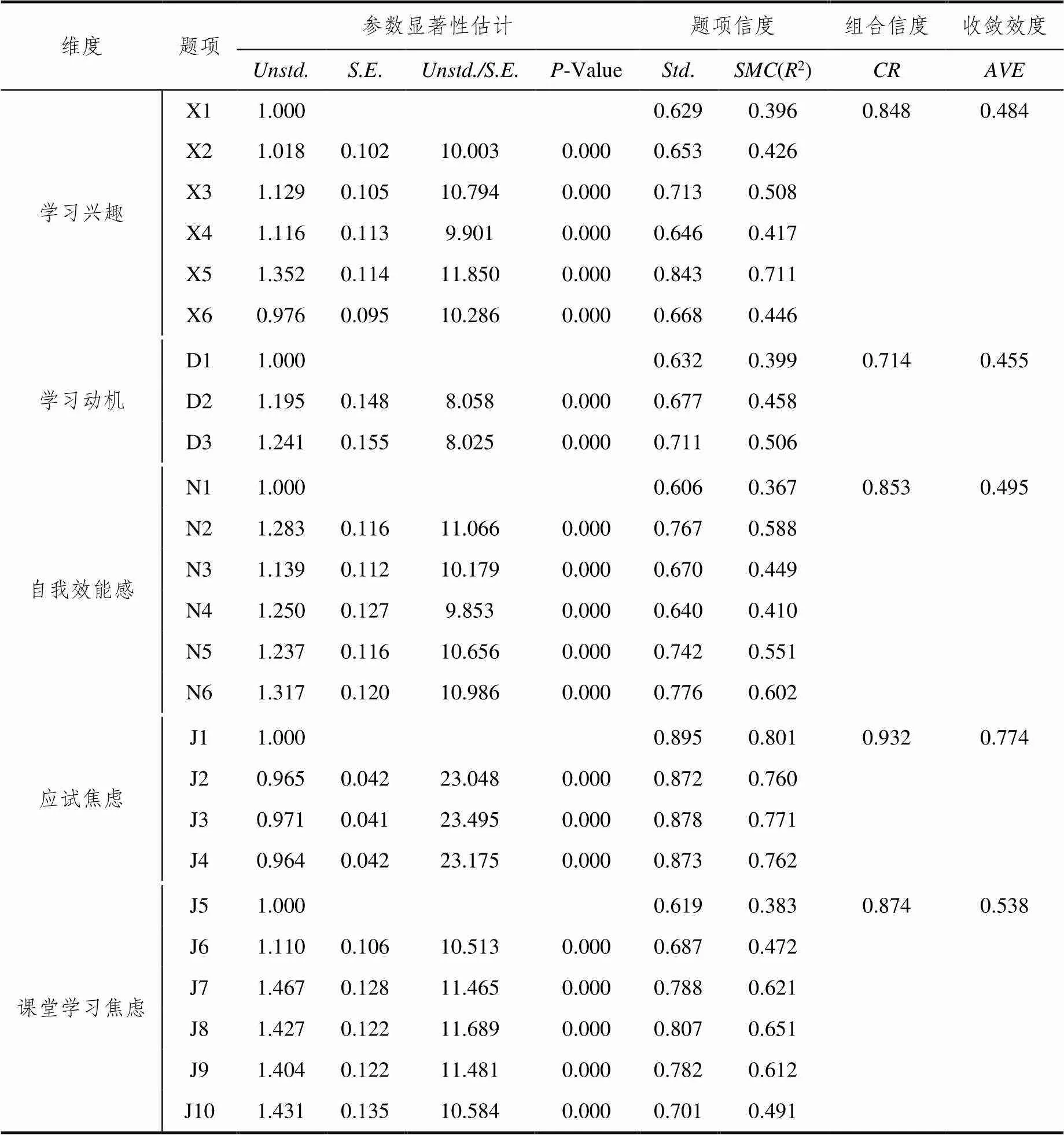
表1 因素负荷量与信度及收敛效度

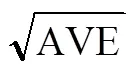
表2 各维度收敛效度与区分效度

综合表1、2来看，量表在以下3方面均达到较为理想或可以接受的水平：各维度对维度内每一题项的个别解释能力；各维度对所含题项的平均解释能力；各维度（应试焦虑和课堂学习焦虑作为一个维度参与计算）之间的区分效度．

3.2 结构模型分析

对图1进行结构模型分析运用了ML估计法，得到的模型拟合指数结果见表3．显见c2/<3、>0.9、>0.9、<0.08、<0.08，均达到理想标准[24]．

表3 模型拟合指数

如表4所示，高等数学学习兴趣对学习焦虑的影响，高等数学学习焦虑对自我效能感的影响均达到负向非常显著（<0.001）；高等数学学习兴趣对自我效能感的影响、高等数学自我效能感对学习动机的影响均达正向非常显著（<0.001）；高等数学学习兴趣和学习焦虑对学习动机的直接影响均未达显著性水平（值分别为0.553和0.189）．也就是说，前述假设1、2、5、6成立，假设3、4不成立．

对于成立的4个假设而言，其标准化估计值显示：学习兴趣每增加一个标准差，学习焦虑将降低0.981个标准差，自我效能感将增加0.381个标准差；学习焦虑每增加一个标准差，自我效能感将降低0.296个标准差；自我效能感每增加一个标准差，学习动机将增加0.822个标准差．结构模型的2值分别为0.445、0.760和0.511，按照已有参考标准[25]，均达到了中度或高度的影响力水平．

表4 模型回归权重和假设成立情况

3.3 中介效应分析

中介效应分析的结果显示：高等数学学习兴趣对学习动机影响的总效应显著（0.509，<0.001）；学习兴趣对学习动机的直接效应不显著（=0.553），间接效应显著（0.429，<0.001），表示中介效应存在且表现为完全中介．显著的中介路径表现为两条：学习兴趣通过自我效能感对学习动机的中介效应显著（0.313，<0.001）；学习兴趣通过学习焦虑影响自我效能感，进而影响学习动机的链式中介效应显著（0.239，<0.01）．

运用Bootstrap进行5 000次运算后，得出了各个影响效应的置信区间结果：学习兴趣影响学习焦虑的95%置信区间为[-0.756, -0.571]；学习兴趣影响自我效能感的95%置信区间为[0.292, 0.595]；学习焦虑影响自我效能感的95%置信区间为[-0.665, -0.357]；自我效能感影响学习动机的95%置信区间为[0.468, 1.217]．以上各95%置信区间均不包含0，同样体现了完全中介效应及其对应路径的显著性．

4 结论与讨论

4.1 高等数学学习兴趣对学习动机的影响

有研究表明：大学生的内在学习动机是高层次学习参与的原动力[26]，提升内在学习动机将促进大学生学习参与的有效性．但在教学实践中需要进一步追溯哪些因素对内在学习动机有显著影响，这些影响作用又是如何发挥的等问题．研究结果显示：在高等数学学习领域，高等数学学习兴趣对学习动机的影响主要以间接形式存在，且显著性水平为<0.001．

要达到促进大学生高等数学学习深度参与，进而达成较好学习效果的目标，提升其高等数学学习兴趣应是重要的可行性手段之一．这为从事高等数学教学的教师指明了方向：在教学过程中，不能只顾进度、照本宣科，更要关注学生的学习兴趣．调查结果显示：在课堂上为学生提供探究的机会、鼓励组织学生参加不同级别的高等数学竞赛、适时介绍数学家的趣闻轶事等是提升学生高等数学学习兴趣的较有效的手段．

对于主观上认为高等数学枯燥乏味的学生而言，需要使其认识到高等数学与初等数学有联系亦有不同，初等数学学习的“折戟”经历并不影响在高等数学学习中实现“逆袭”．需要从对高等数学解题规范过程的模仿、对难题的挑战、对题目所涉数学思想方法的感悟、对高等数学知识的贯通式理解等过程逐步建立高等数学的学习兴趣．教师不能奢望一本教材或一套课件“包打天下”，而是需要对教材进行“专业化”处理，这里的“专业化”主要指的是实现高等数学教学与学生所在专业的深度融合，可以与专业教师相互配合，开展高等数学教研活动时邀请学生所在专业的教师参与进来，努力在高等数学课堂上提供与所教学生专业背景相匹配的例子，从提高学生获得感的角度发展其学习兴趣．

4.2 高等数学学习自我效能感的中介作用

高等数学学习兴趣对学习动机的间接影响体现为两条路径．在其中一条路径中，自我效能感作为独立的中介变量存在．学习兴趣每增加一个标准差，自我效能感将增加0.381个标准差；自我效能感每增加一个标准差，学习动机将增加0.822个标准差．前者与已有研究结果相似[6-7]，反映出数学学习兴趣对自我效能感的影响是跨学段的，在不同阶段的数学学习中存在普遍性．后者则表明，自我效能感对学习动机尤其是内在动机的影响显著．自我效能感对学习动机的作用能够预测学生的课堂学习行为[27]．

高等数学学习兴趣对内在动机的影响主要通过自我效能感发挥，鼓励、帮助学生形成积极的、可控的自我效能感，而非消极的、听天由命式的自我效能感，将能够实现这种影响效力的提升．如对学生的高等数学作业批改，重视以个体纵向进步作为评价指标，而非仅按预设的统一标准评价；了解不同学生高等数学学习自我效能感的缺失性因子有哪些，以求因材施教、对症下药；运用罗森塔尔效应，通过正面的教师反馈帮助学生建立起对高等数学学习的自我成功预期，实现自验预言[10]的积极心态．

4.3 高等数学学习焦虑的中介作用

高等数学学习焦虑对学习动机的直接影响表现不显著，这与已有研究不一致[28]．其原因可能是，已有研究主要针对青少年一般化的学习，没有聚焦于高等数学学习．相比一般的学习材料而言，高等数学的抽象程度较高，如果不理解数学对象的本质，很难达成较好的学习效果．可能导致学习焦虑与学习动机关系不显著的结论．从另一方面看，当学生在外部力量的驱动下学习时，更容易感到紧张和焦虑[29]．而研究者主要针对的是大学生高等数学学习的内部动机，因此得到了影响不显著的结果．

中介效应分析的结果显示，高等数学学习焦虑受学习兴趣的负向影响，同时负向影响自我效能感．这与已有针对小学生或中职生的研究结果一致[18-19]，同样体现了相关维度影响路径普遍存在的特征．或者说，在高等数学学习兴趣间接影响学习动机的另一条路径中，学习焦虑和自我效能感构成了链式中介，需要帮助学生适度降低焦虑程度，以提升自我效能感水平．

2018年10月，教育部印发的《关于加快建设高水平本科教育全面提高人才培养能力的意见》中指出，应“加大过程考核成绩在课程总成绩中的比重”．在高等数学教学实践中，过程考核能够促进学生的学习，对学习焦虑的缓解作用也是可以预见的．经过一学期的高等数学学习，学生面对的是“毕其功于一役”的期末考试，应试焦虑的情况较为严重．表1中学习焦虑的两个子维度的统计结果也说明，高等数学的应试焦虑水平远大于课堂学习焦虑．有必要通过实质性的过程考核分解和缓冲课程考试的应试焦虑，如对回答教师提问、完成随堂小测验、参与课堂讨论、分享学习感想等活动进行合理赋分，在综合考评中加权计算，使学生意识到课程的成绩评定不只是期末完成一张考卷，更是对自己高等数学学习的综合反馈．在完成各项平时学习任务的过程中，逐渐淡化对终结性课程考试的焦虑，实现自我效能感和学习动机水平的提升．

4.4 研究展望

研究者分析了高等数学学习兴趣对学习动机的影响，并运用实证研究方法对影响路径和影响程度进行了中介效应分析．遗憾的是，问卷调查实施时，为降低学生的防备心理，没有要求填写姓名或学号等个人信息，分析时无法将调查结果与个体学业成绩建立联系，进而将学业成绩作为因变量，分析各维度对学业成绩的直接或间接影响，以及不同等级学业成绩的学生在学习焦虑、自我效能感、学习动机和学习兴趣等维度可能存在的差异性．同时，研究采用的是横截面式的调研方法，没有对学生的高等数学学习所涉各维度进行追踪研究．后续研究将对问卷设计进一步改进，如设计某一计算公式由学号后两位数字出发计算得出一个数字，要求被调查者填写得出的数字，数据录入时倒推出对应的学号并在期末考试后与个体学业成绩建立匹配．在此基础上引入“是否考研”等作为调节变量，进行追踪研究，以求深入分析各维度对学生高等数学学业成就的影响路径和效力，以及不同学习阶段学生高等数学学习非认知因素的变化．

[1] A BANDURA. Self-efficacy: Toward a unifying theory of behavioral change [J]. Psychological Review, 1977, 84 (2): 191–215.

[2] 边玉芳．学习自我效能感量表的编制[J]．心理科学，2004，27（5）：1 218–1 222．

[3] 焦彩珍．初中生数学学习兴趣及自我效能与数学学业成绩的关系[J]．数学教育学报，2008，17（2）：44–46．

[4] 陈美英，项东阶．中学生数学学习自我效能感的初步研究[J]．河北师范大学学报（教育科学版），2008，10（4）：44–47．

[5] 庄鸿娟，刘儒德，刘颖，等．中学生社会支持对数学学习坚持性的影响：数学自我效能感的中介作用[J]．心理发展与教育，2016，32（3）：317–323．

[6] 杜宵丰，刘坚．八年级学生“数学兴趣”“数学自我效能感”“学习坚持性”与“数学成就”的关系研究[J]．数学教育学报，2017，26（2）：29–34．

[7] 何声清，綦春霞．师生关系和数学学习兴趣对数学学业成绩的影响——自我效能感及数学焦虑的链式中介作用[J]．教育科学研究，2018（12）：47–54．

[8] 田仕芹．高等数学学习自我效能感的调查分析[J]．数学教育学报，2011，20（5）：66–69．

[9] 徐向红．大学生高等数学学习自我效能感的培养[J]．高等函授学报（自然科学版），2009，22（6）：40–42．

[10] 张春兴．教育心理学——三化取向的理论与实践[M]．杭州：浙江教育出版社，2003：294，296，329，313．

[11] 王光明，宋金锦，王兆云．高中生数学学习非智力特征调查问卷的编制[J]．数学教育学报，2015，24（3）：17–27．

[12] 裴昌根，宋乃庆，刘乔卉，等．数学学习兴趣测评指标体系的构建与验证[J]．数学教育学报，2018，27（2）：70–73．

[13] 吴洪艳，刘晓琳．初中生数学学习兴趣问卷编制与现状调查[J]．数学教育学报，2017，26（2）：50–54．

[14] 刘芳．江苏省高中生化学学习兴趣和学习动机的调查研究[J]．化学教学，2015（6）：22–26．

[15] 李雪平．大学生的一般自我效能感与学习动机的相关研究[J]．教育研究与实验，2012（5）：84–88．

[16] 陈英和，耿柳娜．数学焦虑研究的认知取向[J]．心理科学，2002，25（6）：653–655，648．

[17] 王凤葵，罗增儒．数学焦虑的研究概况[J]．数学教育学报，2002，11（1）：39–42．

[18] 张婕，黄碧娟，司继伟，等．乡镇小学生的数学焦虑与数学成绩：数学自我效能感和数学元认知的链式中介作用[J]．心理发展与教育，2018，34（4）：453–460．

[19] 施俊，陈建东，袁德正，等．“3+4”试点班中职生数学焦虑状况的调查研究[J]．数学教育学报，2015，24（3）：91–95．

[20] 章建跃．中学生数学学科自我监控能力[M]．上海：华东师范大学出版社，2003：107–109．

[21] 熊建华．中学生数学焦虑及相关因素的调查研究[D]．南京：南京师范大学，2005：38．

[22]  FORNEL C, LARCKER D F. Evaluating structural equation models with unobserved variables and measurement error [J]. Journal of Marketing Research, 1981, 34 (2): 161–188.

[23]  HAIR J F, BLACK W C, BABIN B J, et al. Multivariate data analysis [M]. 7th ed. New Jersey: Pearson Prentice Hall, 2009: 123.

[24] 王济川，王小倩，姜宝法．结构方程模型：方法与应用[M]．北京：高等教育出版社，2011：19–21．

[25]  URBACH N, AHLEMANN F. Structural equation modeling in information systems research using partial least squares [J]. Journal of Information Technology Theory and Application, 2010, 11 (2): 5–40.

[26] 于倩，刘金兰，赵远．大学生学习动机对学习参与及学业成就的影响研究[J]．大连理工大学学报（社会科学版），2018，39（6）：100–106．

[27]  WAN Z H. Exploring the effects of intrinsic motive, utilitarian motive, and self-efficacy on students’ science learning in the classroom using the expectancy-value theory [J]. Research in Science Education, 2019 (2): 1–13．

[28] GILMAN R, ANDERMAN E M. The relationships between relative levels of motivation and intrapersonal, interpersonal, and academic functioning among older adolescents [J]. Journal of School Psychology, 2006, 44 (5): 375–391.

[29] 罗丽芳，朱俊萍．不同动机类型学生的学习策略与学习焦虑的比较研究[J]．福建师范大学学报（哲学社会科学版），2018（1）：154–159．

1．学习兴趣维度

（1）高等数学有趣．

（2）我喜欢探究高等数学公式和定理的来龙去脉．

（3）如果有高等数学竞赛活动，我会主动报名参加．

（4）伟大的数学家是我奋斗的榜样．

（5）我喜欢做高等数学的难题．

（6）谈起高等数学的相关知识，我思如泉涌，口若悬河．

2．学习动机维度

（1）高等数学非常难学，但它能给我成就感，所以我喜欢它．

（2）在高等数学学习中，只要我付出努力，就会取得好成绩．

（3）遇到高等数学难题，只要我坚持思考，就能够解决．

3．自我效能感维度

（1）我觉得凭我的能力，可以学好高等数学．

（2）我觉得自己高等数学学得挺好．

（3）瞄准目标完成高等数学学习任务对我而言较为轻松．

（4）在学习高等数学遇到困难时，我会觉得自己不行．

（5）多数情况下，我有把握准确回答高等数学老师的课堂提问．

（6）在高等数学学习方面，我有自己的理由充分的见解．

4．学习焦虑维度

（1）当你想到第二天要参加高等数学考试时．

（2）当你参加高等数学随堂测验时．

（3）当你准备高等数学期末考试时．

（4）当你在事前不知道的情况下参加一次高等数学测验时．

（5）当你听其他同学解释一道高等数学题时．

（6）当你走进教室准备上高等数学课时．

（7）当你开始学习新一章的高等数学内容时．

（8）当你学习某一个新的高等数学公式或定理时．

（9）当你听老师讲高等数学课时．

（10）当同学让你解释某一个高等数学知识时．

Research on the Relations of College Students’ “Learning Interest” “Self-efficacy” “Learning Anxiety” “Learning Motivation”

LI Peng, CAO Li-hua

(College of Mathematics and Statistics, Shenzhen University, Guangdong Shenzhen 518060, China)

The enhancement of college students’ motivation for college mathematics learning can promote their deep participation in learning. To clarify the influencing factors and paths of learning motivation and to respond in a targeted manner during the teaching process may help improve the efficiency of higher mathematics teaching. This study used the structural equation modeling method to investigate college students and found that the influence of higher mathematics learning interest on learning anxiety and self-efficacy was negative. The influence of learning interest on self-efficacy was positively significant. The impact of self-efficacy on learning motivation was similar. Learning anxiety and self-efficacy appeared to have a complete indirect effect on the path of learning interest on motivation. Based on the above results, suggestions are proposed for providing students with opportunities for inquiry, encouraging participation in competitions, paying attention to individual progress, and attaching importance to process assessment during the teaching of higher mathematics.

learning motivation; learning interest; self-efficacy; learning anxiety; structural equation modeling

G442

A

1004–9894（2021）04–0097–06

李鹏，曹丽华．大学生高等数学“学习兴趣”“自我效能感”“学习焦虑”“学习动机”的关系研究[J]．数学教育学报，2021，30（4）：97-102．

2021–04–11

广东省教育科学“十三五”规划2020年度项目——师范生学科育人能力检测模型构建与运用研究（2020GXJK351）；广东省高等教育教学改革项目——数学师范生“翻转课堂”教学能力提升研究与实践；基于新工科应用型人才培养的地方院校高等数学课程教学改革与实践

李鹏（1980—），男，山东枣庄人，副教授，博士后，硕士生导师，主要从事数学课程与教学论研究．曹丽华为本文通讯作者．

[责任编校：陈汉君、陈隽]