整合技术的数学问题解决框架及其应用

谭 奇，袁智强

整合技术的数学问题解决框架及其应用

谭 奇，袁智强

（湖南师范大学 数学与统计学院，湖南 长沙 410081）

信息技术融入数学问题解决是促进信息技术与数学教学深度融合的途径之一．整合技术的数学问题解决框架为此提供了行动指南，它包括3阶段9环节：准备阶段（理解问题含义、抓住关键信息、思考技术功效）、解答阶段（实现问题条件、探索可能结论、制定解题方案、实施解题方案、书写解题过程）和反思阶段（分享解题思维）．以上述框架为主线、以符号中介理论与工具化理论为桥梁，采用测试调查、任务式访谈和文档收集等方法收集数据，分析一个中学生使用动态数学软件GeoGebra实现数学问题解决的过程．研究发现：该生在整合技术的数学问题解决过程中充分展示了整合技术的数学流畅性；数学教育技术对于学生是一种心理工具，对于作为研究者的教师是一种起中介作用的人工制品．研究启示：夯实数学基础知识，提高学生数学问题解决能力；开展数学软件培训，提升学生数学教育技术素养；运用动态数学软件，发展学生整合技术的数学流畅性．

整合技术的数学问题解决；整合技术的数学流畅性；符号中介理论；工具化理论；GeoGebra

1 问题提出

信息技术与学科教学深度融合已成为教育信息化2.0时代的重点关注问题之一[1]．教育部发布的《普通高中数学课程标准（2017年版）》中将六大数学核心素养培养的最终目的指向了学生数学问题解决能力的提升[2]，因而探索信息技术融入数学问题解决的途径具有十分现实的意义．在此过程中，整合技术的数学流畅性（techno-mathematical fluency）也逐渐成为人们关注的聚点之一[3]．根据Barron等人的观点，“流畅性”是指重组知识的能力，创造性地、恰当地表达自己的能力以及产生和生成信息的能力．它需要一个终身学习的过程，在这个过程中，个人不断地应用他们所知道的知识来适应变化，并获得更多的知识，以便更有效地将技术应用到他们的工作和个人生活中[4]．事实上，随着“数学数字能力”（mathematical digital competency）这个研究领域的发展，学者们提出了“整合技术的数学素养”（techno- mathematical literacy）和“整合技术的数学流畅性”两个概念．前者旨在描述存在于特定工作场所中的以数字技术为中介的功能性数学知识；后者是在“信息技术流畅性”的基础上发展而来，它包括将数学和技术这两种类型的背景知识和技能结合在一起的能力[5-10]．用“流畅性”一词来描述这种能力一方面是为了包含整合技术的数学素养的含义，另一方面是为了把这种能力类比于“语言流畅性”，而这门特殊的“语言”涉及了数学知识和技术知识[3]．所以，用“流畅性”一词来描述整合技术的数学问题解决过程比较合适．然而，国内大量研究都是从教师教学的视角，阐述整合技术的数学问题解决教学相较于传统的数学问题解决教学更有优势，很少有研究从学生学习的视角提供描述学生整合技术的数学问题解决流畅性的案例．

随着免费和开源的动态数学软件GeoGebra在高中数学新教材中的出现，教师将更多地把GeoGebra应用于备课、上课、测试与反馈等数学教学环节[11]．GeoGebra也会逐渐成为中小学乃至大学相关学科的师生进行教学及研究的主流平台[12]．因此，研究者让一名中学生使用动态数学软件GeoGebra探究一些开放型的数学问题，并关注其整合技术的数学流畅性．研究将回答如下两个问题：（1）学生在整合技术的数学问题解决过程中展示的整合技术的数学流畅性如何？（2）在整合技术的数学问题解决过程中，数学教育技术起到了什么作用？

2 理论基础

2.1 符号中介理论

符号中介理论（theory of semiotic mediation，TSM）是在维果斯基提出的“符号中介”（semiotic mediation）概念的基础上发展起来的．它所表达的含义是，教师在分析人工制品（artifact）的符号潜能（semiotic potential）后，根据教学周期组织特定的任务或活动，并特意选择一些相关的人工制品供学生使用，让学生在使用人工制品完成任务或活动的过程中，把他们的个人意义转化为特定的数学意义，以达到教师为学生制定的学习目标．在这个过程中，学生产生的手势、语言（包括口头语言和书面语言）或图画等都被称为“人工制品符号”（artifact signs），教师主要扮演专家向导的角色[13-16]．

从符号潜能的角度来看人工制品，它包含了两层符号联系：一方面，当学生使用人工制品完成力所能及的任务时，浮现在学生脑海中的个人意义与人工制品之间建立了符号联系；另一方面，通过使用人工制品引起的并被专家辨认为是数学的数学意义与人工制品之间建立了符号联系．这说明人工制品充当了学生的个人意义与特定的数学意义之间的桥梁[13-16]．因此，教师需要将人工制品作为数学意义的符号中介工具，把涉及到的人工制品符号转变为数学符号．也就是说，通过录音录像、文档收集等方式收集到的人工制品符号可以作为中介物来解释学生的个人意义——学生的心理活动与数学意义——数学问题的正确解答之间的转化．

2.2 工具化理论

工具化理论（instrumentation theory）的出发点在于区分人工制品和心理工具（instrument）的不同．人工制品的含义更广泛，它泛指各种物质工具．但在给定的情境下，人工制品究竟是什么并不很清楚，它既可以指物质工具的某一项功能，也可以指物质工具整体．心理工具则是指人在使用人工制品完成某项特定任务的过程中，人和人工制品之间有意义的联系．换句话说，心理工具除了包括人工制品以外，还包括工具使用者在使用人工制品过程中发展及应用的技艺（techniques）和心理图式（mental schemes）．“技艺”和“心理图式”的理论背景不同．前者基于教学中的人类学理论（anthropological theory of didactics），研究者重点关注学生通过使用技术工具及通过社会互动发展起来的技艺．后者基于认知工效学，研究者把心理图式的发展作为工具生成（instrumental genesis）的核心[13-18]．

心理工具是一个个体的构念（construct），它具有心理特征，并且与它产生和发展的环境密切相关．Rabardel把心理工具的形成和演变过程命名为工具生成．它被描述为两个过程：（1）工具内化（instrumentalisation），即关于人工制品的不同组成部分的出现和进化，人们逐步认识其潜力和限制，人们的知识指导着人工制品的使用方法，在某种意义上塑造人工制品；（2）工具外化（instrumentation），即关于使用方案（utilisation schemes）的出现和发展，人工制品的潜力和限制影响着人们的问题解决策略和对应的新想法．工具生成的两个过程说明人们的思维能塑造人工制品，人工制品也能塑造人们的思维．目前，工具化理论是国外数学教育技术研究领域中的一种常用方法，它提供了一个分析框架，可以用来分析人类使用特定人工制品时的认知过程[13-18]．因此，基于工具化理论，把动态数学软件GeoGebra及学生使用GeoGebra时的技艺和心理图式看成心理工具，通过观察学生对GeoGebra的操作可以分析学生解决数学问题时的心理过程．

2.3 整合技术的数学问题解决框架

问题解决是寻找问题的有效解决方案或可能结果的过程．在这个过程中，个人会针对问题情境选择适当的先前知识及经验，为完成该目标不断寻找可能的解决路径，并对相关的信息进行重组以发展出可行的方法[19]．20世纪80年代，波利亚的有关数学本质与数学问题解决的观点引发了人们对问题解决的重视．人们开始认识到，数学问题解决与数学内容本身一样重要[20]．Schoenfeld把学生在数学问题解决过程中的表现分为6个环节．（1）读题（reading）：花时间读懂问题的条件；（2）分析（analysis）：试图充分理解问题和条件之间的关系；（3）探索（exploration）：查找与问题中的语境相匹配的相关信息；（4）计划（planning）：确定将要实施的行为顺序；（5）执行（implementation）：有顺序地实施计划中的行为；（6）验证（verification）：问题解决者对解答过程进行回顾与评估[21]．Martin和Grudziecki开发了一个整合数字技术的问题解决框架，共包含13个环节．（1）陈述（statement）：清楚地陈述亟待解决的问题和极有可能做出的行为；（2）辨别（identification）：确认顺利完成任务所需要的数字资源；（3）获取（accession）：查找且获得相关的数字资源；（4）评估（evaluation）：评估这些数字资源的精确性与可靠性及它们与问题解决之间的相关性；（5）解释（interpretation）：理解数字资源所包含的意思；（6）组织（organization）：组织数字资源，使任务得以解决；（7）整合（integration）：将这些资源以相关的组合整合在一起；（8）分析（analysis）：使用支持解决方案的概念或模型来检查数字资源；（9）综合（synthesis）：为实现解决方案，用新方法重组数字资源；（10）创建（creation）：创建新的知识对象、新的信息单元、新的数字输出，以帮助实现解决方案；（11）交流（communication）：在解决问题时与他人互动；（12）传播（dissemination）：向他人呈现解决方案；（13）反思（reflection）：反思成功完成任务的过程[22]．

Jacinto和Carreira基于Schoenfeld[21]以及Martin与Grudziecki[22]的上述研究，提出了整合技术的数学问题解决（mathematical problem solving with technology，简称MPST）框架．它把整合技术的数学问题解决过程分为10个环节．（1）理解（grasp）：梳理问题的情境与条件，了解它所涉及的基本概念；（2）察觉（notice）：初步尝试理解什么是解决问题的成败关键，即可能相关的数学知识和必要的数字工具；（3）解释（interpret）：在思考接近解决方案的数学方法的同时，考虑技术资源的功效；（4）整合（integrate）：在探索性方法中整合技术和数学资源；（5）探索（explore）：利用技术和数学资源探索可能实现解决方案的概念模型；（6）计划（plan）：在对通过探索得到的猜想进行分析的基础上，提出解决问题的途径；（7）创建（create）：执行上面提出的能解决问题的途径，用新方法重组资源以使解题方案成为可能，并创建新的知识对象、信息单元或其它的有助于解决和表达问题的输出；（8）验证（verify）：参与解释或证明基于数学和技术资源实现的解决方案的活动；（9）传播（disseminate）：向相关人员展示解决方案或输出的对象，并思考成功解决问题的过程；（10）交流（communicate）：在处理问题或任务时与相关人员进行互动．它贯穿于整个问题解决过程中[3]．

研究在借鉴上述理论的基础上，提出了更加符合中文表达习惯的整合技术的数学问题解决框架，它包括3阶段9环节．

准备阶段：①理解问题含义，读懂问题，理解问题中给出的条件与结论；②抓住关键信息，抓住问题中给出的可能影响最终答案的关键信息，思考可能会用到的数学知识；③思考技术功效，思考数学教育技术在该问题中是否适用、何处能用及可用哪种功能．

解答阶段：④实现问题条件，尝试用数学教育技术实现问题中蕴含的数学知识；⑤探索可能结论，借助数学教育技术探索问题中的隐含条件，并猜测可能的结论；⑥制定解题方案，根据探索过程，制定大致的解题方案；⑦实施解题方案，根据前面的探索创造新的知识对象，以便实施解题方案；⑧书写解题过程，基于数学知识和数学教育技术操作写出解题过程，作为最终答案的解释与验证．

反思阶段：⑨分享解题思维、展示解题方案和用数学教育技术绘制图形，在交流中反思自己的解题过程．需要说明的是，Jacinto和Carreira提出的MPST框架中的“交流”，既包括学生与同伴的交流，也包括学生与教师的交流．研究发生的场景只涉及到一个研究对象，因此这种交流主要发生在学生与作为研究者的教师之间，具体体现在“分享解题思维”这个环节．这里的数学教育技术主要是指几何画板、网络画板、图形计算器、Cabri3D、Fathom、GeoGebra等．

3 研究设计

3.1 研究对象

L同学是一位14岁的初二男生，就读于中部某省一所地级市的H中学．他非常喜欢数学，其数学成绩也处于班级的中上水平．因此，研究者决定以他为重点对象进行个案研究，详细阐述他的整合技术的数学问题解决过程．参加这项研究时，L同学正处于初二第二学期．他在上个学期已经学习了三角形全等以及等边三角形等数学知识．L同学所在班级的数学老师经常使用几何画板讲解数学知识或探究数学问题，因此，他对几何画板的界面比较熟悉．鉴于动态数学软件GeoGebra和几何画板之间的相似性，研究者仅花了一天时间就帮助他熟悉了GeoGebra的基本操作．

3.2 研究过程

研究者在教会L同学使用GeoGebra后，先后3次使用不同的初中数学开放型问题供L同学运用动态数学软件GeoGebra进行自主探究，并要求他一边操作一边进行口头说明．在此过程中，研究者通过录像的方式进行了详细记录．在探究结束后，研究者对L同学进行了访谈并收集了他创建的GeoGebra文件以及用纸笔详细解答这些问题的过程．以下是第二次探究中使用的问题：

在线段同侧作两个等边△和△（顶点按顺时针顺序排列），且∠<120°，如果点、分别是线段、的中点，那么△是特殊三角形吗？

3.3 数据收集与分析

结合符号中介理论和工具化理论，研究者收集和分析了3种形式的数据，它们构成了三角互证．表1列出了数据收集方式、数据形式及收集该数据的目的．

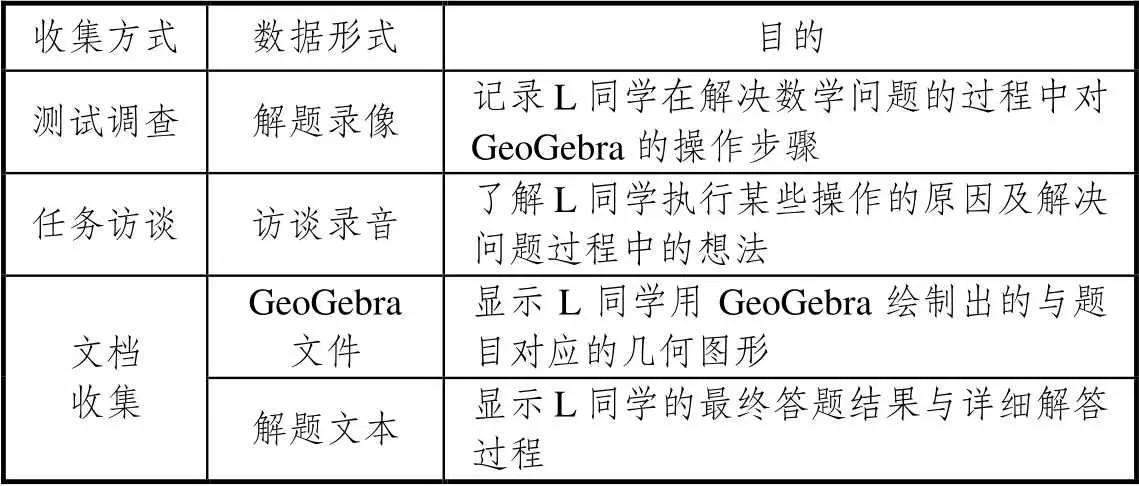
表1 数据收集过程

数据分析分两步：第一步，将录像和录音资料进行文本实录，形成逐字稿；第二步，将整合技术的数学问题解决框架当作编码系统，运用内容分析法分析收集到的数据资料．

4 研究结果

根据整合技术的数学问题解决框架，结合符号中介理论与工具化理论，分为准备阶段、解答阶段和反思阶段3个部分报告研究结果．

4.1 准备阶段

①理解问题含义．L同学一看到问题条件中的“同侧”，就询问了研究者“同侧”这个词的意思，研究者让他先说说自己的理解．他认为两个三角形都处于线段上方或下方就算同侧，如果一个三角形在上方，一个三角形在下方，这就算不同侧．在研究者肯定了他的想法后，他才开始正式思考解决这道题的办法．在这个环节中，L同学的语言作为起中介作用的人工制品，让研究者知道他正在理解问题的含义．研究者的肯定为L同学在解决该数学问题的过程中引导了正确的方向，即研究者扮演了专家向导的角色．

②抓住关键信息．这道题的条件中有两个小细节——“同侧”与“△和△的顶点都按顺时针顺序排列”．如果忽略了这两个小细节，画出来的几何图形与问题中的条件就会大相径庭，L同学极有可能会因为这点小疏忽而得到错误的答案．庆幸的是，L同学在一开始审题时就注意到了这个细节，所以他最后提交上来的GeoGebra文件里的图形完全正确．同时，他也注意到了∠<120°这个条件，意味着点是一个动点，点位置的不同可以导致整个几何图形发生改变，这有可能让△的形状发生变化．研究者对这一环节的分析主要来源于L同学保存的GeoGebra文件，该文件就是L同学在运用GeoGebra解决数学问题的过程中产生的人工制品符号，它是研究者了解L同学的心理图式的重要中介之一．它代表着学生在经过一系列的心理活动后，成功解决了该数学问题．

③思考技术功效．因为研究者事先教过L同学如何使用GeoGebra里的工具以及它们各自的功能，所以他已经知道GeoGebra软件可以用来画等边三角形、寻找线段的中点，还能进行角度的测量以保证在满足∠<120°的条件下进行探索操作．更重要的是，点是一个动点意味着这道问题具有动态性，而软件GeoGebra可以对点进行任意拖动并且操作方便．该环节意味着L同学早已认识了人工制品GeoGebra的潜力和限制，他已经学过的有关GeoGebra的知识指导着他对GeoGebra的操作．这说明L同学在自己和人工制品GeoGebra之间建立了有意义的联系，此时的人工制品GeoGebra转变为心理工具，L同学在经历工具内化的心理过程．

4.2 解答阶段

④实现问题条件．L同学先用GeoGebra里的线段工具画出线段，再在线段上方随意描出了一个点（如图1）．然后，他选中GeoGebra里的正多边形工具，分别点击、和、两点，并输入顶点数为3，这样就画出了两个分别以、为边的等边三角形（如图2）．接着，L同学再次选中线段工具，画出了线段与线段，之后利用中点工具找到了、的中点，在根据题意将它们分别重命名为点和点后，L同学用多边形工具画出△．为了在拖动点时能更清楚地看清△的变化，L同学把它涂成了深色（如图3），考虑到题目要求∠<120°，所以他选中工具栏中的角工具，测量∠的度数（如图4），以保证在探索过程中能快速看出来点处于什么位置时满足题目条件．该环节也是工具内化的过程，L同学的数学知识与技术知识融合，指导着他对GeoGebra的操作.他使用GeoGebra塑造出了新的人工制品，即与问题对应的几何图形．对研究者来说，该几何图形在解释学生的个人意义与数学意义之间的转化过程中起着中介作用．

图1 线段和点

图3 绘制三角形

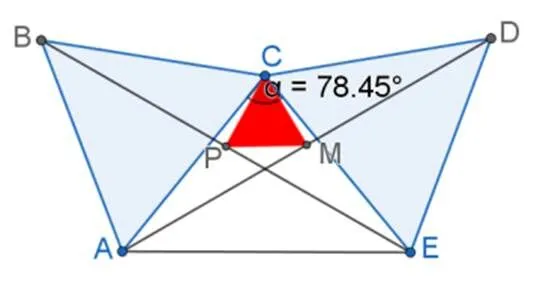
图4 测量角的度数

⑤探索可能结论．现在，L同学已经画出了符合题意的几何图形．下一步，他准备边拖动点边观察△的形状．L同学先在线段的上方拖动点，发现不管∠是否小于120°，GeoGebra左边的代数区显示出来的△的边长始终相等，这意味着画出来的深色△是等边三角形．图5是在上方拖动点使得∠>120°时的情况．他继续移动点，直到点位于线段下方．同样地，他发现无论∠的度数是多少，△始终是等边三角形（如图6）．这样，L同学就知道了题目的最终答案应该是△为等边三角形，但他还需要用数学语言证明得到的结论．该环节说明L同学通过探索画出来的几何图形，发现了一个新结论：△为等边三角形．这意味着用GeoGebra画出来的几何图形与GeoGebra的拖动功能作为人工制品，共同塑造了L同学的思维，让他产生了新的想法．这是工具外化的心理过程．

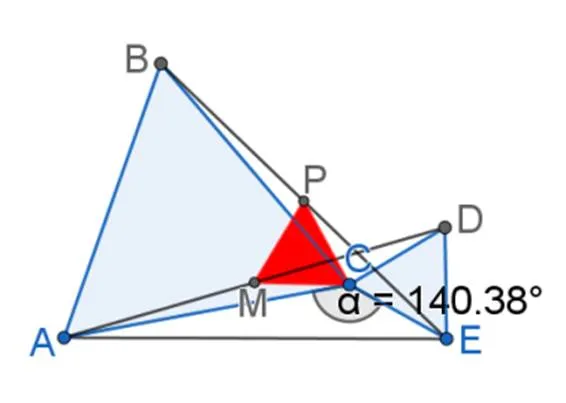
图5 在线段上方拖动点

图6 在线段下方拖动点

⑥制定解题方案．L同学想起来自己在拖动点的过程中还发现了一个有趣的现象：△与△总是同时改变，而且它们的形状看起来是一样的，所以他认为可以用三角形全等的知识来证明这个题目的答案．于是，他决定联系两个三角形全等的判定方法写出一个严格的证明．在这个环节中，L同学也出现了新想法．动态数学软件GeoGebra的功效和限制让几何图形在动态变化的过程中仍保留原有的数学性质，这才让L同学发现△与△的全等关系，进而影响了他下一步的问题解决策略．显然，该环节也凸显了L同学的工具外化过程．

⑦实施解题方案．L同学很快证明了△与△全等（如图7），但这还不够，因为△与它们没有公共边，所以他陷入了困境．于是，他再次回到GeoGebra文件中拖动点，在移动点的过程中，他发现△与△的形状变化也是同步的．为了看得更清楚，L同学隐藏了深色的△，并将△与△涂成了不同的颜色（如图8）．因为这两个三角形与△有公共边，而全等三角形具有对应边相等的性质，所以，他又在草稿纸上证明了△与△的全等关系．这说明L同学通过观察图形想出了严谨的几何证明，从几何直观转向了逻辑推理，把“数”和“形”结合了起来．图8与L同学所写的数学证明就是他为了顺利解答问题而创造出的新知识对象．该环节表明L同学在工具外化的过程中感悟了数形结合的思想，同时创造了新的人工制品符号：以数学语言和数学符号为主要表现形式的解答文本．

图7 学生的解答文本

图8 三角形涂色

⑧书写解题过程．L同学通过证明△与△全等而得到=，这就证明了△是等腰三角形．他再以图8为例，通过“全等三角形对应角相等”这一性质证明了∠=60°．至此，L同学完成了此题的严格证明．他的详细证明过程见图7，这些数学语言就是他对这道题的解释，它们帮助研究者理解L同学在解决问题时的想法．在这个环节中，研究者以L同学的解答文本为中介物分析出了他想要表达的数学意义，该解答文本就是L同学新创造出的人工制品符号．

4.3 反思阶段

⑨分享解题思维．当L同学在草稿纸上写完证明过程后，研究者让他解释了他所写的每一个步骤的来源．这帮助他再次整理了解题思路，也锻炼了他的表达能力．因为L同学在探索过程中已经发现了这样一个事实：不管∠的度数是多少，△始终是等边三角形．所以研究者让他进行思考：如果题目中没有给出∠<120°这个条件，那么证明△是等边三角形的方法是一样的吗？L同学思考了一会儿，打开GeoGebra文件，把点移动到某一个使∠>120°的位置（如图9）．他告诉研究者，这时△与△仍然全等，所以证明方法是类似的，但点位置的不同，会导致∠=60°的证明略有不同．研究者与L同学的交流促使他思考了问题所给条件之外的情况，培养了他的发散思维．在该环节中，L同学借助动态数学软件GeoGebra向研究者讲述了他在解决问题时的心理活动，研究者收集到的音像资料反映了他的心理活动与数学意义之间的转化．L同学再次打开GeoGebra文件，移动点使∠>120°，说明L同学知道GeoGebra具有动态拖动功能，他也知道在拖动点的过程中，GeoGebra会显示出∠的度数．也就是说，L同学具备的关于如何使用GeoGebra的知识指导着他对GeoGebra的操作，图9就是L同学新塑造出的人工制品．这体现了他的工具内化的心理过程．以他的口头语言为中介符号，研究者知道他通过操作GeoGebra发现了△与△始终全等的事实，而L同学发现这个事实的原因正是因为在GeoGebra软件中拖动点时，几何图形原有的数学性质仍保持不变．GeoGebra的潜力和限制促使他得出了“△是等边三角形的证明方法与∠的度数是否小于120°没有太大关系，但点位置的不同，会导致∠=60°的证明略有不同”的结论，这在一定程度上影响了他的问题解决策略．这意味着L同学经历了将GeoGebra进行工具外化的心理过程．

图9 点的移动

5 研究结论

（1）学生在整合技术的数学问题解决过程中充分展示了整合技术的数学流畅性．

学生在“思考技术功效”“实现问题条件”和“探索可能结论”环节会充分运用技术工具的潜能实现题目中或脑海中的数学知识，体现了学生重新组合技术知识与数学知识的过程．学生在“制定解题方案”环节会再次思考重组知识过程中的新发现，进而产生粗略的问题解决方案，这个解决方案就是学生产生的新信息．此外，学生在“实施解题方案”环节会创造新的知识对象，这也是学生产生新信息的过程．学生在“书写解题过程”环节在草稿纸上写出了完整的问题解决步骤，学生的解题文本展现了学生生成信息的能力．学生在“分享解题思维”环节借助GeoGebra绘制出的图像与研究者进行了交流，这是学生创造性地使用数学教育技术手段恰当地表达自己的过程．因此，上述环节既体现了数学知识与技术功效之间的交互，又蕴含了Barron等人对“流畅性”的定义[4]，它们体现了学生“整合技术的数学流畅性”．

（2）在学生整合技术的数学问题解决过程中，数学教育技术对于学生是一种心理工具，对于作为研究者的教师是一种起中介作用的人工制品．

对学生来说，数学教育技术扮演着心理工具的角色．研究结果表明，动态数学软件GeoGebra的潜能可以让学生思考在所给定的问题中是否适合使用该软件及在何处使用该软件，学生综合运用个人所拥有的数学知识和技术知识以实现题目条件，这些都是学生对GeoGebra进行工具内化的过程．从“探索可能结论”环节开始，学生每次使用GeoGebra都触发了新想法的出现，甚至让学生在解决问题的过程中感悟了数形结合的思想，这意味着GeoGebra塑造着学生的思维，即学生在对GeoGebra进行工具外化．对作为研究者的教师来说，数学教育技术是起中介作用的人工制品．作为研究者的教师把学生对GeoGebra的操作以及相应的图像作为了解学生的心理活动与数学意义之间的桥梁，从而明白学生是如何把GeoGebra转变成心理工具，并通过它进行思考、猜想和验证，在工具内化和工具外化的过程中逐渐与之建立起有意义的联系过程．

（3）整合技术的数学问题解决框架为信息技术与数学问题解决深度融合提供了行动指南．

包括3阶段9环节的整合技术的数学问题解决框架在借鉴了国外整合技术的问题解决理论的基础上，使用本土化的语言进行了重新表述，便于一线教师在实践中使用．该框架中的各个环节蕴含了对“流畅性”一词的术语定义，从而可以用来描述学生整合技术的数学流畅性．在以该框架为主线分析学生整合技术的数学问题解决过程时，结合符号中介理论与工具化理论，能细致地描述数学教育技术在学生解决问题时所起到的作用．

6 研究启示

（1）夯实数学基础知识，提高学生数学问题解决能力．

学生不断提取和建构的数学知识有助于成功地解决数学问题[23]．义务教育课程改革的目标之一是让学生学习如何运用他们的知识和技能解决问题，中学数学课程也意在提升学生从数学的视角提出、分析和解决问题的能力[24]．因此，研究者认为夯实教材中的数学基础知识是提高学生数学问题解决能力的基础．以研究中的数学问题为例，它考察的主要知识点是等边三角形和三角形全等，这两部分知识都是初二数学教材中的重点内容．研究结果也展现了学生扎实的数学知识在解决问题过程中的重要性．所以，教师在教学时应立足于数学教材，把基础知识讲透彻，给学生布置习题时要“典型化”，让学生能充分地提取、建构和重组自己已经学过的知识，达到解决一道数学问题，理解一类数学问题的效果．

（2）开展数学软件培训，提升学生数学教育技术素养．

从学习科学的角度看，技术为学习提供了交互性、适应性、反馈、选择、非线性访问、链接式表征、开放式学习者输入以及交流这8种功效[25]，这与“技术赋能学习”的观点不谋而合．研究通过描述学生在数学教育技术支持的环境下解决问题的过程，发现数学教育技术能为学生解决问题提供线索，能帮助学生整合数学知识与技术操作，创造出新的知识对象，并在解决问题的过程中渗透数形结合的思想．因此，教师可以面向学生开展数学软件培训，提升学生的数学教育技术素养，让学生意识到数学教育技术能被应用到不同的数学情境中，并熟悉数学教育技术的功效和限制．这能帮助他们在校外主动利用数学教育技术解决问题，把技术转化为心理工具，在工具内化和工具外化的过程中促进技术功效与数学知识间的交互，进而促进非校园环境中的信息技术与数学学科的深度融合．

（3）运用动态数学软件，发展学生整合技术的数学流畅性．

整合技术的数学流畅性涉及学生对数学知识的灵活运用、对数字工具的熟练使用，以及对问题解决方案的清楚解释和有效交流[3]．研究表明，学生在运用动态数学软件GeoGebra解决数学问题的过程中，需要分析具体在哪里应用GeoGebra，需要组合数学知识与GeoGebra的相关知识创造出新的知识对象，需要向其他人解释自己的问题解决方案、评价反思自己的问题解决过程．换句话说，在解决数学问题时运用动态数学软件GeoGebra有助于发展学生整合技术的数学流畅性．事实上，许多数学教育技术都可以为学生提供一个有效的互动环境，鼓励学生在探索中参与重组知识，生成新的知识，并借助用数学教育技术创造出人工制品，清晰地表达自己的思想．而这正好符合“流畅性”一词的定义．因此，学生可以充分运用动态数学软件解决数学问题，在把数学教育技术转变为心理工具的过程中逐步发展整合技术的数学流畅性．

这里的研究对象是一个成绩中等偏上并且技术素养比较高的学生，该生在运用GeoGebra解决数学问题时没有遇到特别的困难．因此，研究并没有机会展示不同学业水平、不同技术素养的学生在整合技术的数学问题解决过程中的表现，也没有机会刻画整合技术的数学问题解决过程中不同学生之间的交流情况．研究者认为以下问题值得进一步探讨：不同层次学生的整合技术的数学问题解决过程有何差异？学生在整合数学教育技术的环境中以小组合作的方式解决数学问题与独自解决数学问题的过程有何不同？

[1] 袁智强，MARINA MILNER-BOLOTIN．基于TPACK理论的学科教育技术课程研究及启示——以英属哥伦比亚大学“运用技术教数学与科学”课程为例[J]．数学教育学报，2020，29（1）：23-28．

[2] 高翔．20世纪以来中国初中数学课程标准中数学问题解决能力内涵与要求的演变[J]．数学教育学报，2019，28（3）：30-35．

[3] JACINTO H, CARREIRA S. Mathematical problem solving with technology: The techno-mathematical fluency of a student-with-GeoGebra [J]. International Journal of Science and Mathematics Education, 2017, 15 (6): 1 115-1 136.

[4] BARRON B, MARTIN C K, ROBERTS E. Sparking self-sustained learning: Report on a design experiment to build technological fluency and bridge divides [J]. International Journal of Technology and Design Education, 2007, 17 (1): 75-105.

[5] HOYLES C, NOSS R, KENT P, et al. Improving mathematics at work: The need for techno-mathematical literacies [M]. London, UK: Routledge, 2010: 14.

[6] KENT P, BAKKER A, HOYLES C, et al. Techno-mathematical literacies in the workplace [J]. MSOR Connections, 2005, 5 (1): 1-3.

[7] KENT P, NOSS R, GUILE D, et al. Characterizing the use of mathematical knowledge in boundary-crossing situations at work [J]. Mind, Culture, and Activity, 2007, 14 (1-2): 64-82.

[8] van der WAL N J, BAKKER A, DRIJVERS P. Which techno-mathematical literacies are essential for future engineers? [J]. International Journal of Science and Mathematics Education, 2017, 15 (S1): 87-104.

[9] PAPERT S, RESNICK M. Technological fluency and the representation of knowledge: Proposal to the National Science Foundation [M]. Cambridge, UK: MIT Media Laboratory, 1995: 1.

[10] GERANIOU E, JANKVIST U T. Towards a definition of “mathematical digital competency” [J]. Educational Studies in Mathematics, 2019, 102 (1): 29-45.

[11] 左晓明，田艳丽，贠超．基于GeoGebra的数学教学全过程优化研究[J]．数学教育学报，2010，19（1）：99-102．

[12] 王贵军．GeoGebra与数学实验[M]．北京：清华大学出版社，2017：Ⅱ．

[13] BARTOLINI BUSSI M G, MARIOTTI M A. Semiotic mediation in the mathematics classroom: Artefacts and signs after a Vygotskian perspective [M] // ENGLISH L D, BARTOLINI B M, JONES G A, et al. Handbook of international research in mathematics education. New York: Routledge, 2008: 746-783.

[14] MASCHIETTO M. Classical and digital technologies for the Pythagorean Theorem [M] // BALL L, DRIJVERS P, LADEL S, et al. Uses of technology in primary and secondary mathematics education. New York: Springer, 2018: 203-225.

[15] DRIJVERS P, KIERAN C, MARIOTTI M A, et al. Integrating technology into mathematics education: Theoretical perspectives [M] // HOYLES C, LAGRANGE J B. Mathematics education and technology-rethinking the terrain. New York: Springer, 2010: 89-132.

[16] TURGUT M. Sense-making regarding matrix representation of geometric transformations in R2: A semiotic mediation perspective in a dynamic geometry environment [J]. ZDM Mathematics Education, 2019, 51 (7): 1 199-1 214.

[17] RABARDEL P. People and technology - A cognitive approach to contemporary instruments [EB/OL]. (2002-01-01) [2020-07-25]. https://hal.archives-ouvertes.fr/hal-01020705/file/people_and_technology.pdf.

[18] MASCHIETTO M. The arithmetical machine zero+1 in mathematics laboratory: Instrumental genesis and semiotic mediation [J]. International Journal of Science and Mathematics Education, 2015, 13 (1): 121-144.

[19] 鲍建生，周超．数学学习的心理基础与过程[M]．上海：上海教育出版社，2009：172．

[20] LI Y, SCHOENFELD A. Problematizing teaching and learning mathematics as “given” in STEM education [J]. International Journal of STEM Education, 2019, 6 (3): 213-223.

[21] SCHOENFELD A H. Mathematical problem solving [M]. Orlando, Fl: Academic Press, 1985: 297-298.

[22] MARTIN A, GRUDZIECKI J. DigEuLit: Concepts and tools for digital literacy development [J]. Innovation in Teaching and Learning in Information and Computer Science, 2006, 5 (4): 249-267.

[23] 庞丽娟，魏勇刚．论数学问题解决的生态模式[J]．心理发展与教育，2008（3）：124-128．

[24] 朱雁，倪明，孔令志，等．数字时代中的数学教材研究与开发及使用——第三届国际数学教材研究和发展会议综述[J]．数学教育学报，2020，29（2）：94-99．

[25] 徐光涛，许作栋，李英明，等．近二十年学习科学领域的研究脉络与发展趋势——对《人是如何学习的》系列报告的文本分析[J]．华东师范大学学报（教育科学版），2020，38（3）：80-92．

A Framework on Mathematical Problem Solving with Technology and Its Applications

TAN Qi, YUAN Zhi-qiang

(School of Mathematics and Statistics, Hunan Normal University, Hunan Changsha 410081, China)

Integrating information technology into mathematical problem solving is one way to promote the deep infusion of information technology in mathematics teaching.The framework Mathematical Problem Solving with Technology (MPST) provides an action guide for this purpose and consists of three stages and nine steps: Preparation phase (understand the meaning of the problem, grasp key information, consider technology affordances), solution phase (realize the condition of the problem, explore possible conclusions, plan the solution approach, implement the solution approach, write the solution process), and reflection phase (share the problem-solving thinking). Using the MPST framework as the main basis for the study and the theory of semiotic mediation and instrumentation theory as bridges, numerous data were collected of a secondary school student via test survey, interview survey, and document collection for analyzing the process of mathematical problem solvingusing GeoGebra. The research results showed that the student’s techno-mathematical fluency was fully embodied in the process of mathematical problem solving with technology; in addition, technology in mathematics education is an instrument for students and a mediating artifact for teachers as researchers. The research implications include the following: tamping basic mathematical knowledge to promote students’ problem-solving ability, launching mathematical software training to improve students’ literacy in technology in mathematics education, and applying dynamic mathematical software to develop students’ techno-mathematical fluency.

mathematical problem solving with technology; techno-mathematical fluency; theory of semiotic mediation; instrumentation theory; GeoGebra

G632.4

A

1004-9894（2021）04-0048-07

谭奇，袁智强．整合技术的数学问题解决框架及其应用[J]．数学教育学报，2021，30（4）：48-54．

2021-03-26

教育部人文社会科学研究青年基金项目——创新型STEM教师培养的探索性研究（18YJC880115）

谭奇（1999—），女，湖南衡阳人，硕士生，主要从事数学教育研究．袁智强为本文通讯作者．

[责任编校：陈汉君、陈隽]