陶瓷基复合材料结构固有频率与内部损伤分析

2021-08-08汪佳辉吴锦武郭小军胡晓安李龙彪王海涛

失效分析与预防 2021年3期

汪佳辉，吴锦武 ,2,*，郭小军，胡晓安 ,2，李龙彪，王海涛

（1.南昌航空大学飞行器工程学院，南昌 330063；2.江西省微小航空发动机重点实验室，南昌 330063；3.中国航发湖南动力机械研究所，湖南株洲 412002；4.南京航空航天大学民航学院，南京 210016；5.中建一局集团第二建筑有限公司，北京 102600）

0 引言

陶瓷基复合材料（CMCs）因为具有高强度、能承受的环境温度高、具有较低热膨胀系数等优良的性能，已被广泛应用于航空发动机领域[1-3]，如加工制造航空发动机的高压涡轮导向叶片、燃烧室中的火焰筒、加力燃烧室中的隔热罩和尾喷管的调节板等部件。

现阶段，CMCs 已从单向纤维增强发展至二维编织和三维针刺结构[4]。编织陶瓷基复合材料内部细观结构、纤维/基体界面相互作用以及组成材料的属性等细观特征影响CMCs 整体力学及物理性能[5-7]。虽然制作工艺不断改良，但受制于其材料特性，CMCs 在制备过程中可能会存在某些缺陷，如孔隙、各向异性等；因此，利用该材料制造的零部件在工程应用时易受到机械振动的影响而产生损伤[8-10]。在循环载荷作用下，纤维增强陶瓷基复合材料会出现迟滞现象，基体裂纹在循环载荷作用下张开和闭合是出现迟滞现象的主要原因。迟滞回线可表征CMCs 的内部损伤程度[11-13]。

振动问题是制约CMCs 在发动机部件应用的主要瓶颈之一。胡殿印等[14]为了研究二维编织SiC/SiC 复合材料结构振动特性，建立了宏观等效弹性常数预测方法，并在此基础上开展了复合材料平板件的模态分析及试验验证。陈晶[15]研究了针刺C/SiC 复合材料的循环拉压加卸载应力应变曲线特征，分别从时间域和频率域对针刺C/SiC 复合材料梁的振动响应进行了仿真计算。徐雅洁等[16]针对平纹编织陶瓷基复合材料梁的损伤进行振动特性分析，对平纹编织陶瓷基复合材料梁进行振动测试试验，分析平纹编织陶瓷基复合材料梁受损伤之后的非线性振动。Tracy 等[17]为了研究微观结构对纤维陶瓷基复合材料损伤的影响，使用统计学方法，得到了陶瓷基复合材料的微观结构对材料开裂的影响。Chateau 等[18]在宏观和微观方面分析单向SiC/SiC 陶瓷基复合材料的损伤演化规律，通过电子显微镜定量和定位分析力裂纹，并建立基体断裂、纤维断裂的演化模型。Cahill 等[19]在计算机模拟仿真的条件下对单向复合材料损伤分析，最后研究分析出裂纹的扩展与加载条件、材料形状无关，裂纹只沿纤维方向扩展。

本研究重点从陶瓷基复合材料结构固有频率与内部损伤关系的研究出发，基于作者以前对陶瓷基复合材料细观力学的循环加卸载迟滞模型[20]，分析其对应的界面脱粘比、纤维断裂概率的试验值以及与理论值之间的误差。再次根据循环加卸载试验时的材料固有频率，建立固有频率衰退与弹性模量衰退、界面脱粘比和纤维断裂概率之间关系，从而达到可通过陶瓷基复合材料结构固有频率的变化来反映材料内部损伤的目的。

1 试验材料

试验所需的编织SiC/SiC 复合材料结构几何尺寸如图1 所示。SiC/SiC 主要包含纤维、基体和界面层三部分。其中，纤维采用Boxiang III SiC 纤维作为增强体，基体采用Boxiang 的固体PCS 进行PIP 致密化，界面层采用化学气相渗透（CVI）方法在SiC 纤维表面沉积热解碳（PyC）界面层。Boxiang III SiC 纤维的材料属性见表1。

表1 Boxiang III SiC 纤维基本参数Table 1 Basic parameters of Boxiang III generation SiC fiber

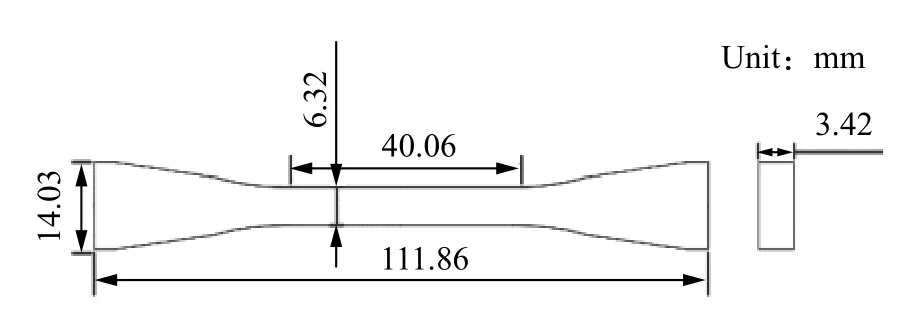
图1 编织SiC/SiC 陶瓷基复合材料试样几何尺寸Fig.1 Structural geometry of braided SiC/SiC ceramic matrix composites

以Boxiang III SiC 纤维作为增强纤维，将纤维编织成预制体（纤维体积含量Vf为40%），采用CVI 方法在编织体纤维表面沉积热解碳（PyC）界面层，界面层厚度约为150 nm。采用聚合物浸渍裂解（PIP）方法在SiC 纤维编织体中制备SiC 基体。得到SiC/SiC 复合材料后，采用机械加工的方法将其切割成拉伸试验所需样品尺寸。

SiC/SiC 材料属性为：密度约为2 g/cm3、孔隙率约为15%、基体含量Vm约为45%、纤维体积含量Vf为40%，纤维弹性模量Ef=210 GPa，基体弹性模量Em=90 GPa，纤维半径rf=6 μm，纤维的热膨胀系数αf=3.3×10-6/℃，基体热膨胀系数αm=4.6×10-6/℃，复合材料制备温度与工作温度差ΔT=-1000 ℃。由试验得到编织 SiC/SiC 纤维/基体界面剪应力τi=17 MPa 和纤维威布尔模量为m=5，纤维的特征强度为σc=2.0 GPa，基体开裂特征强度σR=102 MPa。陶瓷基复合材料材料试样的峰值应力σm=266.78 MPa。

2 循环加卸载试验

本研究在INSTRON8872 液压伺服疲劳试验机上对陶瓷基复合材料试样展开拉伸加载试验研究，装置如图2 所示。声发射检测采用由4 块PCI-2 采集卡所组成的8 通道型测试系统，采用R80D 压电传感器。振动测试采用PSV-500 激光测振仪与压电陶瓷作为激励对试样进行固有频率测试。

图2 陶瓷基复合材料试样加卸载试验装置图Fig.2 Diagram of experimental device for loading and unloading ceramic matrix composite sample

试验加载速率为0.05 mm/min，试验环境温度为17 ℃，声发射试验阈值为55 dB。首先将试样安装在疲劳试验机上，在加载前利用激光测振仪测量试样的固有频率，随后对试样进行加载，目标拉力为0.5 kN，并且保持载荷3 min，然后卸载（为保护试样和仪器，拉力一般卸载至0.05 kN），再利用激光测振仪测量试样的固有频率。对试样继续加载试验，直到拉力为4.4 kN 时结束，共计16 次。每次施加拉力时对应的材料所承受的应力分别0、24.2、48.5、72.7、87.2、96.9、111.5、121.1、133.3、145.4、169.6、193.8、198.7、203.5、208.4、213.2 MPa，每次试验后从液压伺服疲劳试验机导出试样弹性模量E数据。

试样所承受的载荷循环往复不断增加。在缓慢加载过程中，试样基体所能承受的初始开裂应力小于拉应力时，试样承受的拉应力达到了其最大疲劳应力，内部基体出现裂纹，纤维与基体的界面层产生了脱离[21]；在卸载情况下，试样内部纤维与基体的界面层产生了相反的移动距离，把界面层脱离的区域叫做反向滑移区和滑移区，其中定义界面层反向滑移的区域长度为y；再次加载过程中，试样内部的纤维与基体反向滑移区域出现一个新的滑移，试样内部的界面层脱粘区分为新滑移区、反向滑移区和滑移区，定义试样界面层新产生的新滑移区长度z[22]。试样在卸载和再次加载过程中，其内部的纤维与体积的界面层产生脱离的区域发生了滑移和反向滑移，使得试样在循环加卸载过程中产生的应力-应变曲线出现迟滞现象。

1）当界面部分脱粘时，其循环迟滞回线关系为[22]：

卸载时：

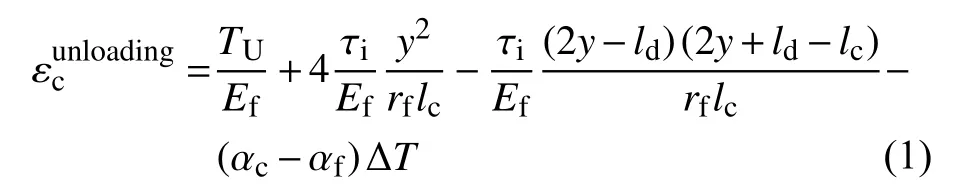
重新加载时：

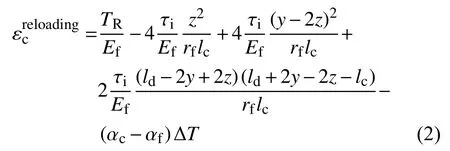
2）当界面完全脱粘时，其循环迟滞回线关系为：

卸载时：

表2 是循环加卸载试验采集的应力、固有频率、弹性模量数据，以及根据式（5）～式（7）计算出来的界面脱粘比（2ld/lc）和纤维断裂概率（q）。

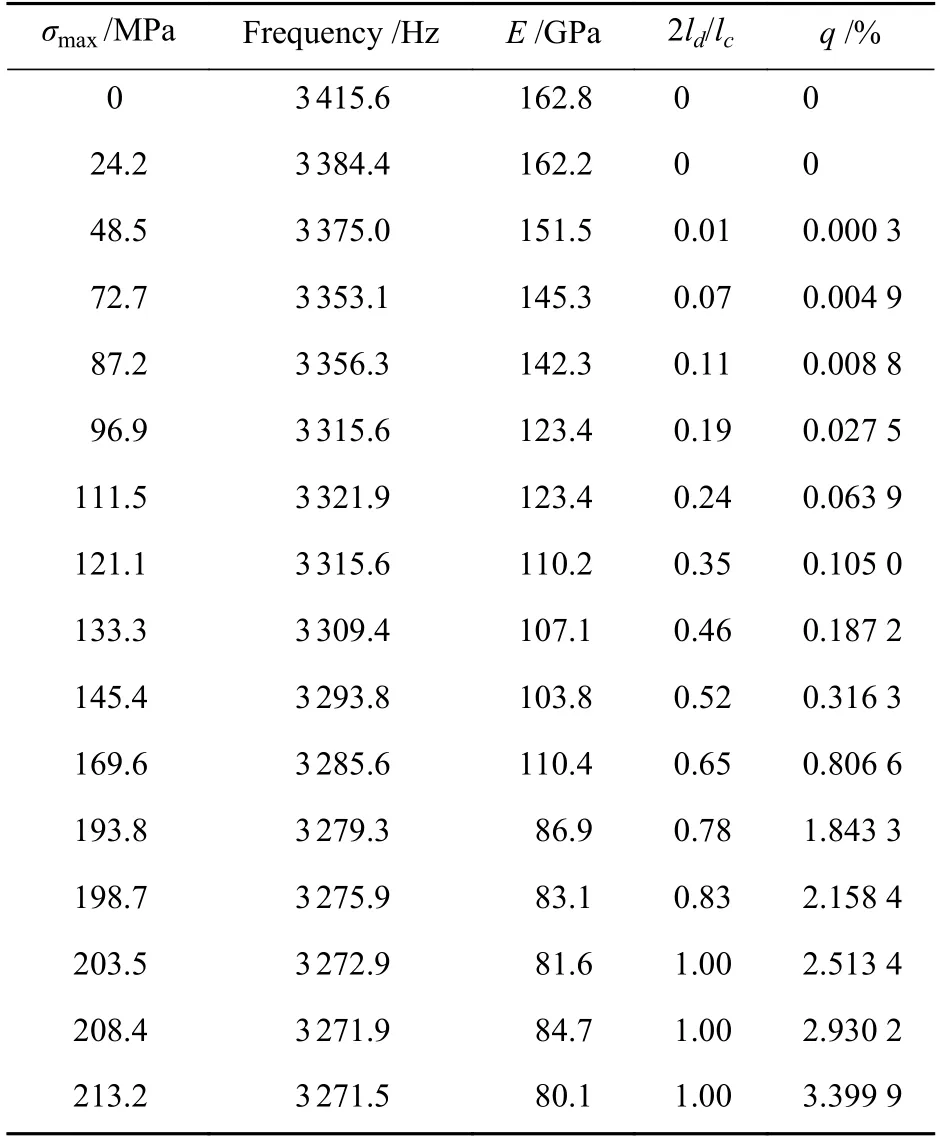
表2 试样结构固有频率随应力变化Table 2 Structural natural frequency of the sample varied with the stress

表2 中试验结果有16 组应力数据，根据的应力大小，选取3 个不同阶段的48.5、96.9、203.5 MPa应力下的数据，分析SiC/SiC 复合材料迟滞回线和界面滑移长度随应力曲线。

图3a 为SiC/SiC 陶瓷基复合材料试样在σmax=48.5 MPa 下的试验值和预测迟滞回线。在该应力下，试样的纤维与基体界面出现纤维部分脱粘，其中纤维断裂概率为0.000 3%；由于纤维断裂概率过低，因此陶瓷基复合材料的循环加卸载的试验值与理论预测迟滞回线的结果相吻合。图3b 为试样在卸载时界面反向滑移长度y和重新加载新界面滑移长度z随应力变化曲线，当y随着应力的减小而增加时，试样的应力从48.5 MPa 卸载至0 MPa，得到y/ld=1；当z随着应力增加而增加，应力增加到10 MPa 以后得到z/ld=1。当σmax=48.5 MPa时，界面部分脱粘，加卸载界面完全滑移。

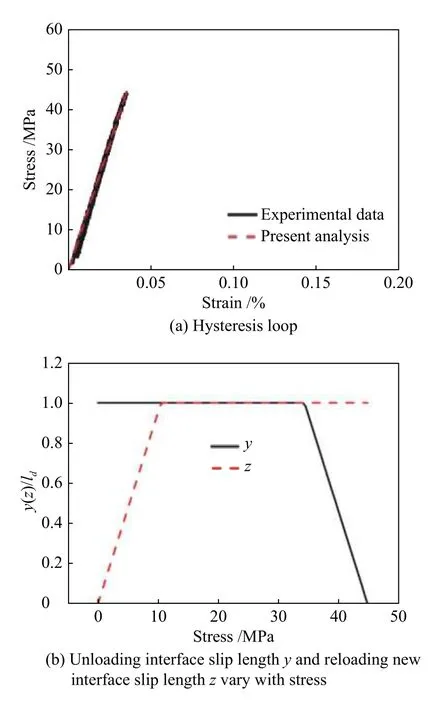
图3 σmax=48.5 MPa 时试样的迟滞回线及滑移长度的变化曲线Fig.3 Hysteresis loop and curve of slip length at σmax=48.5 MPa

图4a 为SiC/SiC 陶瓷基复合材料试样在σmax=96.9 MPa 试验和预测迟滞回线。在该应力下，纤维基体界面部分脱粘，纤维断裂概率为0.027 5%；考虑试样的纤维断裂概率，陶瓷基复合材料的循环加卸载试验值与理论预测的迟滞回线结果几乎没有差异。图4b 为试样在卸载时界面反向滑移长度y和重新加载新界面滑移长度z随应力变化曲线，随着应力缓慢减小，y缓慢增加，当应力卸载到0 时，y尚未达到界面脱粘尖端，即y＜ld；当重新加载时，z随着应力缓慢增加而逐渐增加，应力加载到峰值应力时，得到z＜ld。当σmax=96.9 MPa 时，界面部分脱粘，加卸载界面部分滑移。

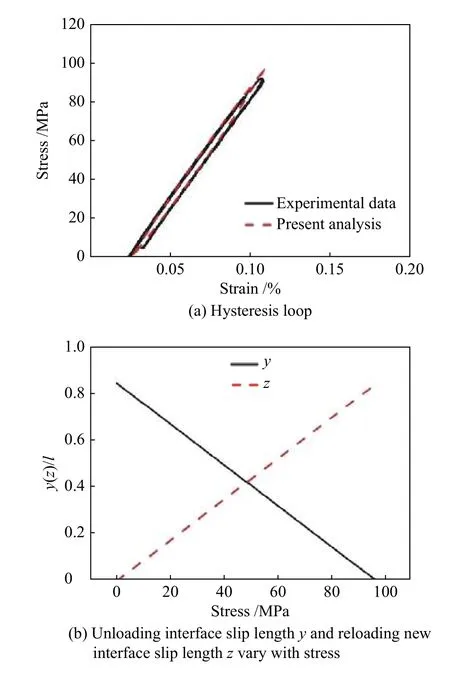
图4 σmax=96.9 MPa 时试样的迟滞回线及滑移长度的变化曲线Fig.4 Hysteresis loop and curve of slip length at σmax=96.9 MPa

图5a 为SiC/SiC 陶瓷基复合材料试样在σmax=203.5 MPa 试验和预测迟滞回线，在该应力下，陶瓷基复合材料试样的纤维基体界面完全脱粘，试样的纤维断裂概率约为2.51%；由于考虑了试样的纤维断裂概率，使得陶瓷基复合材料试样的循环加卸载试验值与理论预测的迟滞回线结果几乎没有差异。图5b 为试样y和z随应力变化的曲线，当y随着应力的减小而增加，界面脱粘比2ld/lc=1（脱粘比为1 表示2 倍的界面脱粘长度等于基体裂纹间距，界面完全脱粘），即y=2ld；z随着应力增加而增加，界面脱粘比2ld/lc=1，即z=2ld。当σmax=203.5 MPa时，界面完全脱粘，加卸载界面部分滑移。

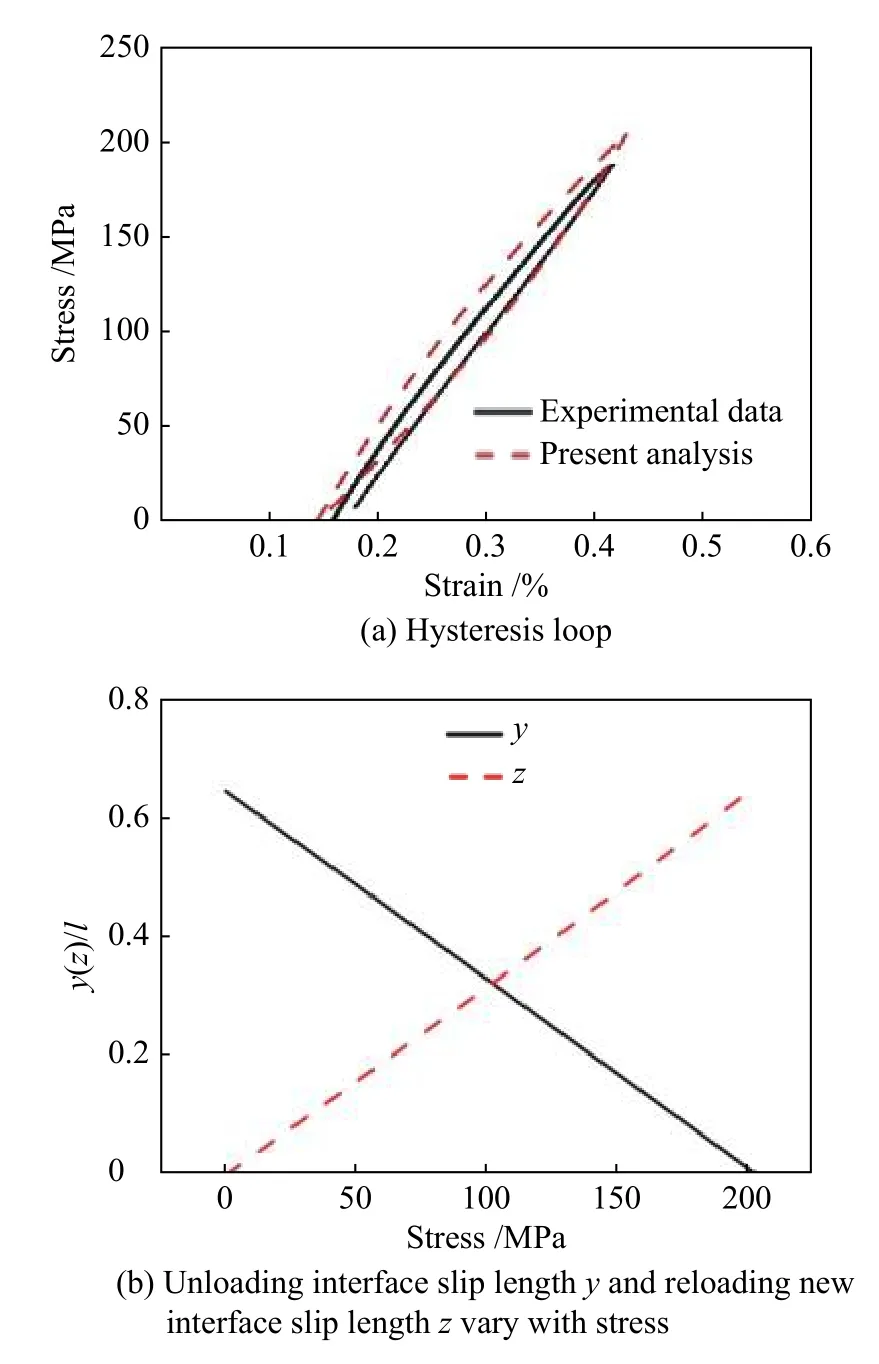
图5 σmax=203.5 MPa 时试样的迟滞回线及滑移长度的变化曲线Fig.5 Hysteresis loop and curve of slip length at σmax=203.5 MPa

3 固有频率与内部损伤分析

由表2 中的数据可得到：1）循环加卸载试验应力与界面脱粘比的关系曲线（图6a），可见，界面脱粘比（2ld/lc）随着应力的增加而变大，直至增加到1 为止（脱粘比为1 表示界面完全脱粘）；2）循环加卸载试验应力与固有频率的关系曲线（图6b），可知，固有频率随着应力的增加而下降，且固有频率与应力呈近似直线变化；3）循环加卸载试验应力与纤维断裂概率的关系曲线（图6c），可知，纤维断裂概率随着应力的增加而变大，且纤维断裂概率在试验前半段几乎没有变化。

由图6b、图6c 可知：当加载应力低于150 MPa时，固有频率与加载应力呈线性变化，纤维断裂概率几乎不增加；当加载应力高于150 MPa 时，固有频率与加载应力呈指数变化，纤维断裂概率与加载应力也呈指数变化；在加载应力为150 MPa 时，其固有频率为3 291.2 Hz，此时SiC/SiC 陶瓷基复合材料内部受力复杂，大大增加了内部纤维的断裂概率。

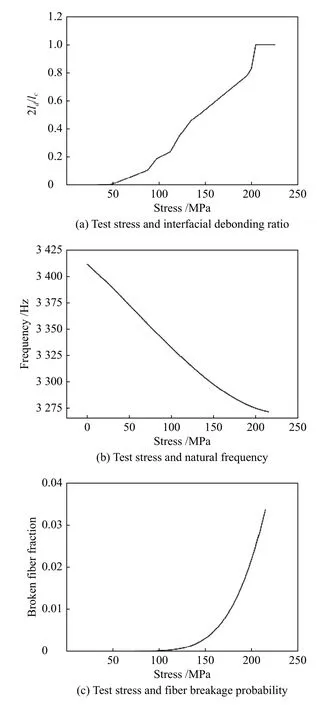
图6 试验应力与界面脱粘比、固有频率、纤维断裂概率的关系曲线Fig.6 Relationship between test stress and interfacial debonding ratio,natural frequency,fiber breakage probability

随着应力的增加，陶瓷基复合材料试样的内部出现了基体开裂、纤维与基体的界面层脱粘的现象，并且纤维断裂的概率逐渐增加，导致陶瓷基复合材料试样的弹性模量大幅度衰减和固有频率的逐渐下降。

定义复合材料固有频率衰退参数Φ为：

定义复合材料弾性模量衰退参数D为：

图7 为试样的固有频率衰退参数Φ与复合材料弾性模量衰退参数D、界面脱粘比2ld/lc以及纤维断裂概率q之间的关系曲线。从图7a 可知，Φ与D呈近似一次函数，固有频率变化与弹性模量变化一致；从图7b 可知，Φ与2ld/lc呈近似指数函数，固有频率衰退2%之后，界面脱粘比迅速增加；从图7c 可知，固有频率在衰退为3%之前，q基本不增加，而衰退参数在3%之后，q急剧增加。也从侧面反映，在循环加卸载试验中，陶瓷基复合材料内部损伤与循环加卸载的应力正相关。

图7 固有频率衰退参数与弾性模量衰退参数、界面脱粘比、纤维断裂概率关系曲线Fig.7 Relationship between natural frequency decay parameter and elastic modulus decay,interface debonding ratio,fiber fracture probability

当Φ=1%时，基体出现开裂，界面发生脱粘，但纤维未断裂；当Φ=4.17%时，D=49.87%，2ld/lc=1，q=2.51%。