解三角形的实际应用

刘园

◆摘  要：解三角形的实际应用问题尤为广泛，既可以解决平面几何问题，也可以应用于实际的测量，作为数学在日常生活中运用的典型，是当前越来越重视对数学实际应用能力的考察的考查的高考热点。本文以解三角形的实际应用教学为例，研究通过正弦定理和余弦定理如何解决实际应用中的距离，高度和角度问题，揭示数学学习生活化的意义。

◆关键词：正弦定理;余弦定理;解三角形

解三角形实际问题是高中数学教学的重点和难点之一，同时也是近几年高考热点之一。我们都知道数学与我们实际生活息息相关，它来源于我们的生活，并应用于日常生活当中，比如：我们如何测量两座城市之间的距离？如何测量一些建筑物的高度？又如何确定轮船的航向等等，这些实际问题的解决都可以转化到数学中解三角形的问题。这类问题基本涉及到正弦定理、余弦定理、三角形面积公式以及三角函数等知识，还蕴含着转化、数形结合、分类讨论等数学思想方法，同时解三角形实际问题还可以培养学生数学运算、数据抽象和数学建模的数学核心素养。

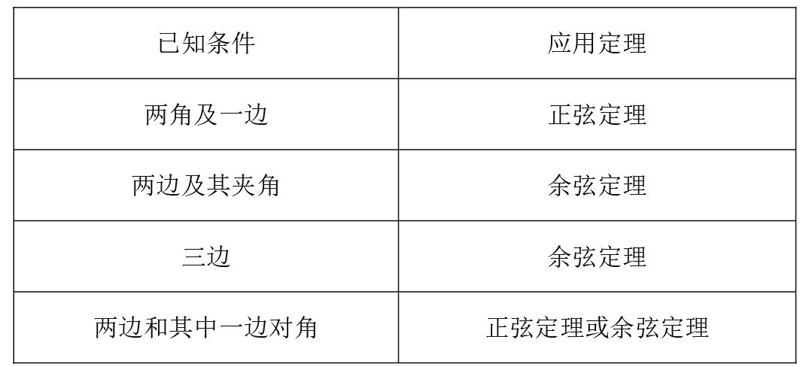
两个定理在解三角形中的选择：

1实例

关于解三角形的实际应用问题，将会通过下面这道自行设计的实际应用题来帮助学生展开分析和理解。

题目：如下图，点A、B、C、D位于同一水平面，假设你位于黄浦江边某定点A处，现手中只有皮尺和测角仪，在不可以过江的前提下，你能否設计出适当的测量方案解决下列实际问题，测量数据可以用字母代替：

1.计算出你到东方明珠塔底端的距离AB;

2.计算出东方明珠塔的高度BE;

3.计算出黄浦江对岸东方明珠塔底端与上海中心大厦底端的距离BD.

分析：根据题目中图形的理解，题目第一问所需要求解的问题实际就是AB的距离，第二问所需要求解的问题实际就是BE的距离，第三问所需要求解的问题实际就是BD的距离，根据题目的要求和实际问题的背景，要求出AB、BE、BD的距离，就要用到解三角形等相关知识，通过学生的建模，构造出实际问题的数学模型即可解决这几个问题。

通过这道实际探究题的建模分析可知，解三角形在实际生活中的应用非常广泛，诸如在实际问题中求距离、高度等都可以运用解三角形的有关知识去解决。在解决实际问题的过程中，我们要学会把实际问题转化为数学问题，根据实际问题建立出适当的数学模型，然后通过数学知识进行推理演算，得出数学模型的解，再还原到实际问题当中，最终实际问题就可以得到解决。

2结束语

数学生活化，生活数学化。数学知识来源于日常生活，也服务于日常生活，有效地将理论和实践紧密结合，这样才能体现出数学的价值所在。在实际的教学当中，要让学生学会用数学的眼光看待实际问题，并学会用数学的理论知识解决日常生活中的问题，这可能就是我们学习数学的真正意义吧！

参考文献

[1]尹建堂，简议解斜三角形的实际应用.数学通讯，2006.12.

[2]牛永亮.解斜三角形应用举例[J].课题与研究：教学论坛，2011（2）：75-75.