大导程螺母滚道型面数值分析与验证*
2021-08-02邢永胜
邢永胜,欧 屹,梁 医,王 凯
(南京理工大学机械工程学院,南京 210094)
0 引言
滚珠丝杠副作为机械设备中最常用的关键元件,能够实现螺旋运动与直线运动的转换,运动平稳且噪声小,兼具可逆性好与效率高的优点[1]。进入21世纪后,滚珠丝杠副向着“速度”与“精度”兼顾的目标前进[2],而增大导程是实现高速化的主要途径。而大导程螺母内滚道的标准磨削加工过程中出现的螺母体与螺杆碰撞现象限制了其发展,因此在原有设备下,采取螺杆倾角小于滚道螺旋升角的干涉磨削方式进行内滚道加工[3]。
对于干涉磨削加工过程,Harada H指出,该方法中螺母体内表面与套筒轴的碰撞限制了螺母体长度,螺母滚道只能够获得部分完美的哥特式圆弧,砂轮与滚道的过度磨削现象导致剩余部分与理论型面产生较大偏离,却并未分析过度磨削带来的影响[4-5]。 Hegedus G对圆锥螺杆在螺母体内的空间位置进行了分析,依据套筒与螺母体的最小距离建立数学模型,分析了安全距离下不发生碰撞的螺杆长度[6]。范东风对比出了不同加工参数下,干涉加工获得砂轮型面的差异,发现倾斜角度越大砂轮变得越尖锐,却没有分析与实际磨削量的联系[7]。以上研究对磨杆碰撞问题进行了分析,未能获得完整滚道型面。对于磨削过度问题,台湾学者发现在特定情况下,根据啮合原理计算的砂轮,不能加工出需要的螺纹型面,为此采用新的几何方法计算砂轮廓形,同时调整砂轮倾角,来避免螺纹加工过程中的下切问题[8]。陶丽佳将磨削过度问题转化为砂轮与理论螺杆转子的干涉问题,进行了理论分析,利用ADAMS进行干涉校验来证明螺杆钻子磨削过程未发生过度磨削现象[9]。而实际加工过程中,过度磨削问题并不需要完全避免,保证良好的工作型面下,小区域的过磨削区域是可以接受的。
本文对干涉磨削加工下大导程螺母滚道型面,考虑存在较小过度磨削区域对磨削余量的影响,提出用动态法平面截取砂轮廓形计算最终滚道型面。建立误差模型表征磨削余量增量,设计临界角指标表征最终滚道是否符合设计要求,并分析了砂轮直径、设计接触角与磨削余量增量、临界角的关系。
1 螺母内滚道磨削分析
1.1 螺母内滚道建模
螺母滚道法向截形为哥特式双圆弧,根据已有的建模方法[4],在母线坐标系O1-x1y1z1中,螺母滚道母线表达式:
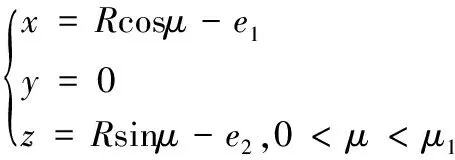
(1)
其中,R表示滚道半径值,μ为法向截形相位角参变量,μ1=cos-1((R1-rm+e1)/R),R1为大径的二分之一,e1,e2为偏心距。建立单侧螺母滚道表达式:
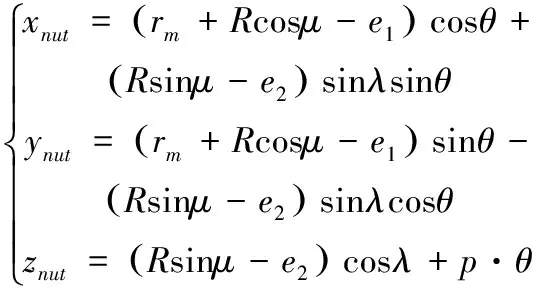
(2)
式中,θ为参变量,表示母线从起始绕z轴转过的角度;rm表示公称半径,λ表示螺旋升角;p表示螺旋参数。内滚道干涉磨削与标准磨削图如图1所示。
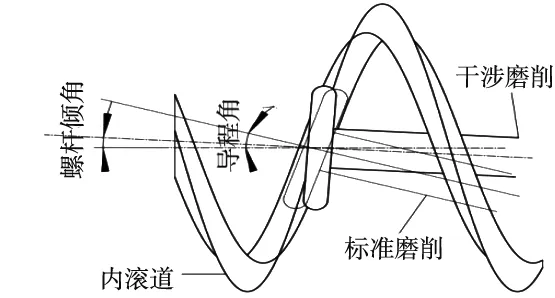
图1 内滚道干涉磨削与标准磨削
建立砂轮与螺母的关系坐标系,如图2所示。其中O-xyz是螺母坐标系,z轴沿轴线方向;O1-x1y1z1是螺母滚道法向型面即母线坐标系,两坐标系中x1轴与x轴重合,原点O1与O点的距离为rm(公称半径),y轴逆时针方向旋转λ(螺旋升角)得到y1轴;O′-XYZ是砂轮坐标系,Z轴沿砂轮轴线方向,X轴与x轴重合,原点O′与O点的距离为a(中心距),y轴逆时针方向旋转Σ(砂轮偏转倾角)得到Y轴。
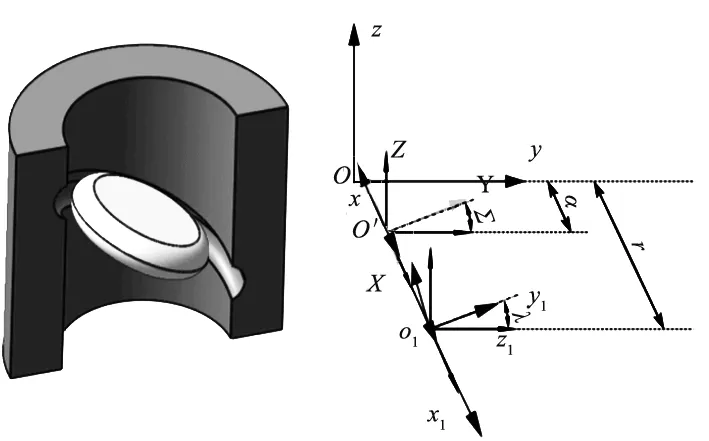
图2 螺母滚道与砂轮坐标关系
则螺母螺旋面在砂轮坐标系O′-XYZ中的表达式为:

(3)
1.2 螺母滚道成形机理
根据一般的螺旋成形机理,根据坐标变换和啮合原理,已知螺母滚道形状或砂轮廓形其中之一,即可求解得到另一个。
如已知刀具廓型数据(Zt,Rt)在自身坐标系O′-XYZ中的表达式:
Xtool=Rtcosφ,Ytool=Rtsinφ,Ztool=Zt
(4)
式中,φ是参变量,它是半径线R与平XO′Z面的夹角。根据接触线条件式[7]方程(5),可以得到磨削接触点。将接触点转换到理论滚道型面的任一法平面下,可以得到滚道型面法向形状。
f(Rt,Zt,φ)=nx(-RtsinφcosΣ+ZtsinΣ)+
ny(Rtcosφ+a)+pnz=0
(5)
仿真发现,基于式(5)的啮合原理计算不能得到滚道最终型面。为此重新思考螺母滚道成形机理,为了简化加工过程,假设螺母与砂轮处于加工接触状态,将加工过程离散为多个绝对静止状态,每个状态不同之处在于砂轮与螺母滚道的相对位置。每一个绝对静止状态下砂轮都会对滚道进行磨削,此时滚道型面可认为是所有绝对静止状态下砂轮磨削产生的滚道型面的综合。
理论上,理论滚道型面与廓形数据构成的砂轮在任何绝对静止状态下应该是处于恰好接触状态。然而,将理论螺母滚道与砂轮处于加工接触状态且绝对静止,不考虑其他误差,实际滚道型面相比于理论滚道型面产生误差时,可认为是螺母理论滚道部分区域被砂轮廓形侵入造成的过度磨削现象。
2 滚道加工型面分析
2.1 动态法平面截取数值方法计算滚道型面
动态法平面截取法的中心思想与上文中简化的螺母滚道成形过程一致,即滚道型面可认为是所有绝对静止状态下砂轮磨削产生的滚道型面的综合。换言之,工件某处的滚道型面可以认为是多个绝对静止接触状态下砂轮对该处所有作用的叠加。对滚道型面误差判定的主要参照是理论滚道型面,因此建立理论滚道型面与砂轮廓形的加工接触状态图。
图3是动态法平面示意,图3a是动态法平面原理的三维空间表述,图3b是某法平面截取的理论滚道与砂轮型面。求参数为θ的理论滚道法向平面与砂轮的交点,而后利用坐标变换将交点转换到理论滚道法向平面坐标系O2-x2y2z2下。参数为θ的理论滚道法向平面本质上为图1中O1-x1y1z1螺母滚道母线坐标系沿着钢球中心螺旋线旋转角度θ得到的,即O1-x1y1z1坐标系中原点就是理论钢球中心螺旋线上一点。由此可知,理论滚道与任何法平面的相交曲线皆为哥特式双圆弧,与θ无关。
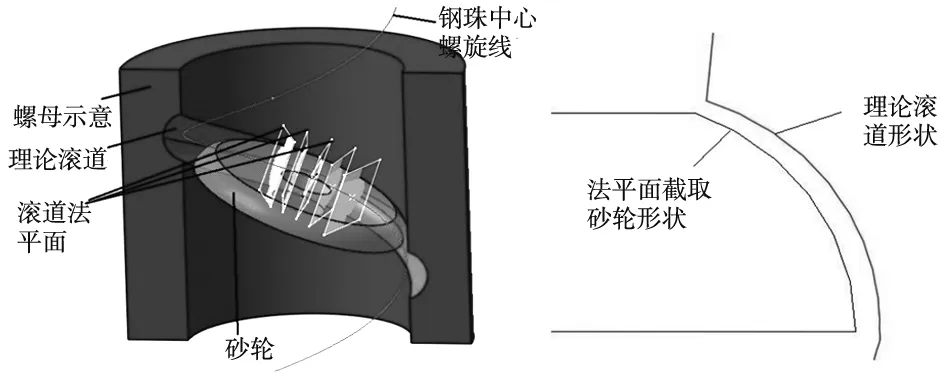
(a) 动态法平面 (b) 某法平面截取结果图3 动态法平面法示意图
采用空间平面的点法式方程建立工件坐标系下法平面。通过定点M(x0,y0,z0),其法向量为n={A,B,C}的平面方程:
A(x-x0)+B(y-y0)+C(z-z0)=0
(6)
定点M采用螺旋线上钢球中心点,与滚道建模时坐标系O2-x2y2z2类似,钢球中心点的轨迹方程为:
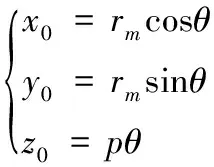
(7)
任一点的切向量为:

(8)
该切向量就是过M点滚道法向平面的法向量n={A,B,C}。将式(7)、式(8)带入式(6),得到法向平面的方程式(9):
f(x,y,z,θ)=x0′(x-x0)+y0′(y-y0)+z0′(z-z0)
(9)
联列法向平面的方程(9)与工件坐标系下砂轮表达式,人为设定参数θ步长,然后将砂轮廓形数据代入,即可得到工件坐标系中一系列参数θi的法平面与砂轮的交点。根据坐标变换将法平面与砂轮的交点分别变换到相同参数θ的动态法平面坐标系O2-x2y2z2中,得到各自法平面下的离散点沿y2轴方向的分量皆为0,与螺母滚道母线坐标系O1-x1y1z1下母线表达式(1)对应。
2.2 数据处理与误差模型建立
在母线坐标系O1-x1y1z1中,将所有计算结果与滚道母线分别表示如图4所示。采用相位区间筛选方法获得第一象限内边缘数据作为滚道形状,如图5所示。

图4 动态法平面截取到的砂轮廓形包络曲线簇 图5 相位区间筛选数据原理
改进误差模型[8],实际型面离散数据集的一阶导数采用差分法后精度高且易求,计算出任意点的法线与理论曲线的交点,然后求二者距离作为廓形误差。如图6所示,圆弧部分代表理想滚道型面,它的函数方程式已知的。B(xi1,zi1)、C(xi2,zi2)、D(xi3,zi3)三点为实际型面数据,根据C、D点可以求得B点切线斜率k,再求得B点法线斜率,联立法线表达式与圆弧方程求得交点B′(xi4,zi4),则BB′点距离可以求得。
过B点的法线直线可表示为:
(10)
故型面误差为:
(11)

图6 误差模型示意
同时引入整体误差Ε作为评价指标:
(12)
式中,N为实际型面上过度磨削区域离散点个数。整体误差Ε用于表征磨削余量增量,增量大会加速砂轮磨损,单工序中砂轮修整次数增多。
临界角指标指计算参数接触角α应该小于完美哥特式弧形的临界角度αc,并留有一定安全值,如图7所示。故干涉加工下螺母滚道过度磨削区域采用整体误差E评价,在加工过程中比非过度磨削区域需要更多的加工余量,完美哥特式弧形区域的大小采用临界角度αc评价,决定最终滚道是否合格。
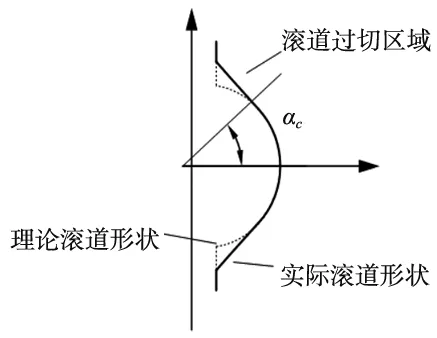
图7 临界角示意
2.3 滚道干涉原理分析
大导程螺母滚道的过度磨削现象与砂轮的廓形有关,在接触状态下砂轮将侵入理论螺母滚道。根据成形机理[9],在加工过程中破坏螺旋面形成线,滚道会产生型面偏差。因此将螺母理论滚道置于砂轮坐标系式(3),用平行于XOY平面的面去截取滚道,得到任一砂轮廓形下与滚道相交曲线,查看该平面中砂轮半径Ri与相交曲线的位置关系。
图8a为平行于坐标系XOY且平面参数为Z的平面与螺母理论滚道型面的相交情况,根据式(4)红色虚线为该平面下的砂轮圆,由图8b可以看出二者可能存在两个相交区域,曲线之间相切相交区域,和滚道边缘与砂轮圆的相交区域。而第二个相交区域就是造成滚道过度磨削的主要原因,从数学角度上来解释,就是该相交曲线上存在到砂轮轴距离小于砂轮圆的部分。因此砂轮直径会影响到滚道弧形的临界角度αc,即影响过度磨削程度。

(a) 任一砂轮圆与相交曲线的空间示意 (b) 砂轮圆与相交曲线的二维示意图8 砂轮圆与相交曲线的关系
3 滚道型面仿真与试验验证
以某型号的螺母为例进行仿真计算,参数如表1所示。
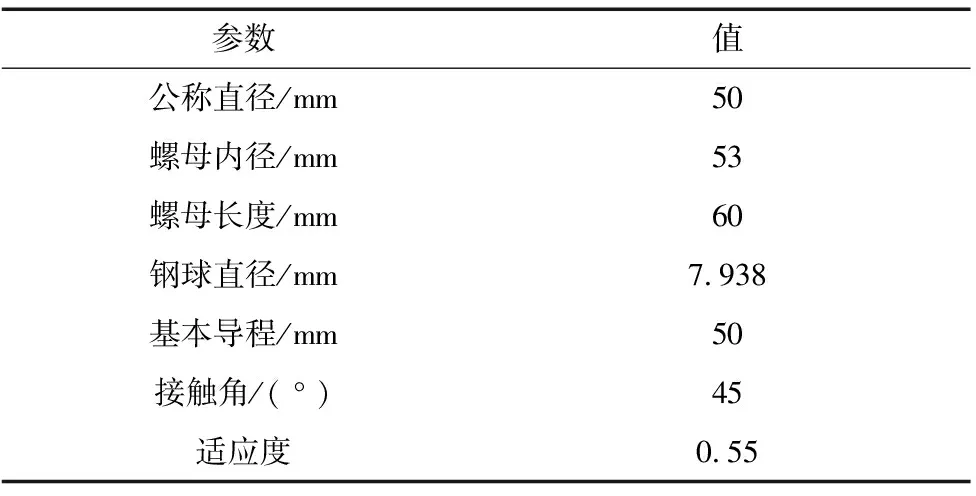
表1 某型号螺母参数
3.1 螺母滚道过度磨削程度与砂轮直径的关系
由于螺杆倾角与砂轮直径、螺母长度存在一定的关系[5],而螺母直径需大于磨杆外径,小于螺母内径,在此范围内设置对比试验研究过度磨削程度与砂轮直径的关系。
预设参数分为两部分,第一部分为三组螺杆倾角与砂轮直径的较优组合,第二部分为三组0°螺杆倾角与不同砂轮直径分别组合。

表2 螺杆倾角、砂轮直径对临界角度、整体误差影响
第一部分预设参数下,螺杆倾角与砂轮直径同时发生变化,临界角度αc增大,砂轮直径总变化值为10 mm,临界角从61°变为67°(最大值),整体误差值E保持较小值,滚道过度磨削现象趋于消失。
第二部分预设参数下,单独减小砂轮直径也可以增大临界角,砂轮直径从35 mm变化到25 mm过程中,砂轮直径总变化同样为10 mm,临界角增大幅度达20°左右,远远满足设计要求,整体误差从8 μm减小为3 μm,同样表明过度磨削区域的大幅缩减。结合图9可以看出,得到的滚道法向截形更接近理论值。
对于滚道磨削加工过程,较小的磨杆倾角意味着磨杆与螺母体发生碰撞干涉的几率小,但实际磨削量增加导致磨削效率低。而较大的磨杆倾角实际磨削量小,砂轮磨削效率高,且不易磨损。
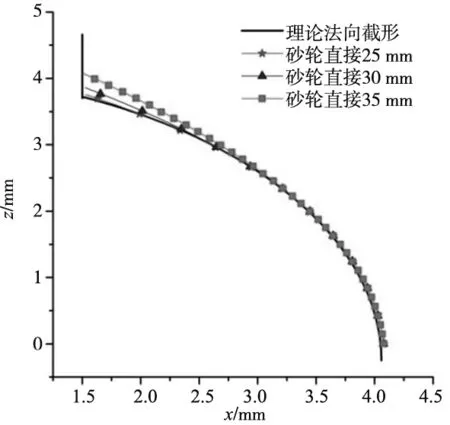
图9 螺杆倾角0°下不同砂轮直径磨削后滚道法向截形
3.2 螺母滚道过度磨削程度与设计接触角的关系
合格螺母滚道的临界角αc需要大于设计接触角α,螺母设计接触角一般小于丝杠接触角3°左右[13],可以减小空回程角。设计对比试验,螺杆倾角0°,砂轮直径30 mm,改变设计接触角α研究临界角αc的变化。
如表3所示,等幅减小设计接触角,临界角以较小幅度增加,可认为间接满足了设计要求。考虑到实际接触角相对于设计值存在一定的上下浮动,当临界角比实际接触角微大时,认为不满足设计要求。

表3 接触角对临界角度影响
3.3 试验验证
不同程度的过度磨削引起的磨削增量难以直接验证,却可通过良好磨削工况下工序中砂轮修整次数间接表示。考虑到操作可能导致的螺杆与螺母碰撞与实际修整次数本身存在弹性量,采用螺杆倾角0°,分别取直径为35 mm与25 mm的砂轮进行内螺纹滚道磨削。如图10所示,内螺纹磨床型号为汉江SK7620A,磨削工艺为粗磨与精磨,进给量为0.02 mm。
如表4所示,不同过度磨削程度会影响到砂轮修整次数。砂轮直径从35 mm替换为25 mm,良好磨削工况下砂轮单次工序修整次数从5次变为2次,表明实际磨削量的减小与加工效率的提升。通过测量两个工件的实际临界角,考虑测量误差下实际临界角均处于表2中的仿真误差允许范围内。

表4 不同砂轮直径对临界角影响

图10 7620A磨床干涉磨削螺母过程
4 结论
根据螺母滚道建模与砂轮联合计算,得到螺母滚道干涉误差模型,通过实例仿真分析,得出以下结论:
(1)大导程螺母滚道完整形状可以通过滚道多个法向平面截取砂轮廓形得到,干涉加工容易发生滚道过度磨削现象,是由于某一砂轮圆平面与滚道的交线存在两处相交区域。
(2)通过增大砂轮直径可以增大加工滚道圆弧的临界角,满足滚道设计要求,但需与螺杆倾角匹配,保证磨削效率。改变设计接触角,可以间接满足接触角设计要求。
(3)误差模型中整体误差E可表征滚道过度磨削引起的磨削余量增量,不同程度过度磨削现象引起的磨削增量变化可通过稳定磨削工况下砂轮修整次数差异间接验证。
