泡沫铝填充薄壁梁斜向碰撞的仿真研究
2015-11-30肖志�k��刘洪斌��孔春玉�
肖志 �k��++刘洪斌��++孔春玉��++莫富灏��++李素雯

摘要:采用有限元仿真技术研究了泡沫铝填充薄壁梁不同角度斜向碰撞下的吸能特性。分析了泡沫铝密度、壁厚、长宽比等设计参数对临界角和平均碰撞力的影响,并拟合出平均碰撞力和各设计参数及碰撞角度的解析式。结果表明,泡沫铝填充薄壁梁的临界弯折角小于无填充薄壁梁,并且泡沫铝密度对临界角的影响最大。随着横截面宽度从70 mm增大到90 mm,无填充薄壁梁弯折临界角从6°增大到9°,而泡沫铝填充薄壁梁弯折临界角度则没有明显改变。壁厚越厚泡沫铝填充薄壁梁的弯折临界角越大,但无填充薄壁梁弯折临界角不变。平均碰撞力和碰撞角度存在指数函数关系,且反比于长宽比平方、正比于壁厚和泡沫铝密度的指数幂。
关键词:斜向碰撞;薄壁梁;耐撞性;填充泡沫铝;临界角;碰撞力
中图分类号:U467。3文献标识码:A
金属薄壁梁作为一种低成本、高效率的缓冲吸能结构,被广泛应用于车辆、船舶、航空航天等几乎所有交通工具的碰撞吸能装置中\[1\]。现代汽车中大部分框架都设计成薄壁梁结构, 通过在碰撞过程中自身的变形来吸收能量。薄壁梁的碰撞主要有轴向溃缩和弯折两种变形模式。当前大量的研究主要从薄壁梁的轴向碰撞进行研究,包含材料、厚度和截面形状等对薄壁梁碰撞特性的影响\[2-3\]。
但是,现实中的薄壁梁吸能结构只承受纯轴向碰撞载荷的形态很少发生,大多数情况下,载荷方向会偏离薄壁结构轴线,或者与轴线方向存在一定夹角\[4\]。大量的实验和数值仿真均表明,薄壁梁在轴向载荷作用下发生渐进压溃变形能有效地吸收碰撞能量,而斜向碰撞下的能量吸收随着碰撞角度的增加而急剧减少。研究表明,对特定的薄壁梁存在一个临界角度,当碰撞角度大于此临界角度时,薄壁梁将发生侧向弯曲,其吸能能力迅速下降\[5\]。Nagel等人\[6\]研究了变截面管件在斜向碰撞载荷下的力学响应,包括单边渐弱(single taper)管和双边渐弱(double taper)管。研究结果表明,这种渐弱的设计能有效提高薄壁梁件的吸能能力,同时双边渐弱比单边渐弱更加有效。
湖南大学学报(自然科学版)2015年
第10期肖志等:泡沫铝填充薄壁梁斜向碰撞的仿真研究
Thornton\[7\]研究发现薄壁梁通过填充其他材料的方式可以增强耐撞性。泡沫铝是其中一种填充功能材料,兼有金属和泡沫的特性,其压缩应力应变曲线有高而宽的应力平台,大量能量在近似恒定应力下被吸收。这种特性使泡沫金属具有很高的吸能效率,可以广泛应用于汽车、轨道列车和航空航天等行业,因此,泡沫铝填充薄壁梁引起了广泛的关注\[8\]。徐雅晨等\[9\]研究了泡沫铝填充铝合金圆管的轴向压缩性能;Hanssen等\[10-11\]通过大量试验研究了动、静载荷作用下泡沫铝填充薄壁梁的轴向压溃行为;谢中友等\[12\]进行了泡沫铝合金填充圆管的三点弯曲实验研究;Yang等\[13\]对无填充薄壁梁和泡沫铝填充薄壁梁在斜向加载下的吸能进行了多目标优化;Santosa等\[14\]进行了泡沫铝填充薄壁梁的轴向静态压缩试验和数值研究,发现平均压溃力增量和泡沫铝抗压强度、薄壁梁横截面积成线性关系;Ahmad等\[15\]研究了泡沫铝填充圆锥管在斜向动态载荷下的吸能特性。目前,研究人员从斜向准静态和动态加载两方面研究薄壁梁,提出了评价斜向碰撞的关键指标——平均碰撞力\[2\]。
本文通过有限元数值仿真,以平均碰撞力为衡量指标研究不同斜向碰撞角度下泡沫铝密度、薄壁梁壁厚、长宽比等参数对泡沫铝填充薄壁梁吸能特性的影响。定量分析不同碰撞角度下平均碰撞力与泡沫铝密度、长宽比、壁厚等参数的关系,为泡沫铝填充结构优化设计和工程应用提供参考。
1有限元模型
1。1有限元模型描述
考虑到接触问题的高度非线性、大变形和材料的复杂性,本文利用显式非线性有限元程序LSDYNA研究泡沫铝填充薄壁梁斜向碰撞的响应。有限元基准模型如图1所示,薄壁梁的横截面宽度b=80 mm,总长度l=480 mm,薄壁梁壁厚t=1。5 mm,泡沫铝密度ρ=340 kg/m3,碰撞角度为α。考虑到在实际应用中吸能结构一般是连接在一个质量相对很大的物体上,因此在薄壁梁末端附加400 kg质量。薄壁梁以13。41 m/s的初速度斜向撞击无摩擦刚性墙。
图1有限元模型示意图
Fig。1Finite element model
薄壁梁采用BELYTSCHKOLINTSAY类型壳单元,厚度方向5个积分点,泡沫铝采用单点积分8节点体单元以避免体积锁定。为了防止零能模式的产生,采用基于刚度的沙漏控制。刚性墙采用壳单元并使用刚性材料(MAT_20)模拟。薄壁梁和泡沫铝的自接触采用ATUOMATIC_SINGLE_SURFACE,薄壁梁和泡沫铝的接触采用AUTOMATIC_SURFACE_TO_SURFACE,静态和动态摩擦因数分别为0。3和0。2,薄壁梁和泡沫铝与刚性墙的接触采用AUTOMATIC_SURFACE_TO_SURFACE。壳单元和体单元大小分别为4 mm和5 mm。
薄壁梁材料为低碳钢,密度ρ=7 800 kg/m3,弹性模量E=205 GPa,泊松比ν=0。3,屈服应力σy=220 MPa。使用汽车碰撞中广泛使用的分段线性材料模型(MAT_24),其工程应力应变曲线参考文献\[5\],见表1,本文未考虑应变率效应对碰撞结果的影响。
表1低碳钢应力应变曲线数据
Tab。1Stressstrain hardening data for mild steel
等效塑性应变
工程应力σ/MPa
0。0
220。0
0。005 939 3
250。0
0。016 738
300。0
0。025 750
332。0
0。035 750
352。5
0。051 500
370。0
0。105 250
374。0
由于泡沫铝材料的复杂性,泡沫铝模型的建立在有限元仿真中仍然是一个很大的挑战。LSDYNA提供了几种泡沫铝模型:MAT_26,MAT_63,MAT_75,MAT_83,MAT_126和MAT_154等。文献\[16\]表明MAT_63和MAT_75具有较高的准确性和计算效率。本文选择比较常用的MAT_63号泡沫铝材料模型。
Hou等\[17\]总结了适用于任意密度泡沫铝(MAT_63)的应力应变关系,但是没有考虑致密应变的影响,本文在此基础上考虑致密应变后泡沫铝的应力应变关系,如表2所示。
表2任意密度泡沫铝应力应变关系
Tab。2Stressstrain corresponding relationship
for arbitrary foam density
应变
0
σ*/E*
0。6εD
0。7εD
0。8εD
εD
应力 /GPa
0
σ*
σ*
1。35σ*
0。05 E*
1
表中σ*,E*,εD分别为泡沫铝平台应力、弹性模量、致密应变,主要由基体材料的性质、泡沫材料的相对密度和胞体结构的几何性质决定。泡沫材料的力学性能遵守幂法则\[18\]:
A(ρfoam)=A0(ρfoamρal)n。 (1)
式中:A为泡沫铝材料的性能;ρfoam和ρal分别为泡沫铝密度和铝密度;A0为反映孔壁基体材料性能的因子;n为指数。A0和n通常使用最小二乘法拟合实验数据得到。本文取值参考文献\[19\],见表3。
表3 泡沫铝材料常数
Tab。3Aluminium foam material parameters
σ*
E*
A0 /GPa
0。59
330
n
2。21
2。45
结构的耐撞性主要考虑其吸能能力,一般表征指标是平均碰撞力Fmean。能量的计算有两种方式:一种是通过对力位移曲线积分得到,一种是直接从内能曲线得到,两种方式的差别在2%以内\[20\]。本文直接输出内能数据,再计算得到平均碰撞力。
1。2 模型验证
为了保证有限元模型的有效性,需要对比无填充薄壁梁和泡沫铝填充薄壁梁在斜向碰撞下数值仿真和试验的平均碰撞力、初始峰值和压溃模式。无填充薄壁梁有限元模型通过文献[5]中的力位移曲线和平均碰撞力结果来验证。但是关于泡沫铝填充薄壁梁斜向动态加载的实验数据、理论分析或有限元分析结果未见报道,泡沫铝填充薄壁梁有限元模型通过Reyes等\[19\]对泡沫铝填充薄壁梁静态斜向加载的结果来进行验证。
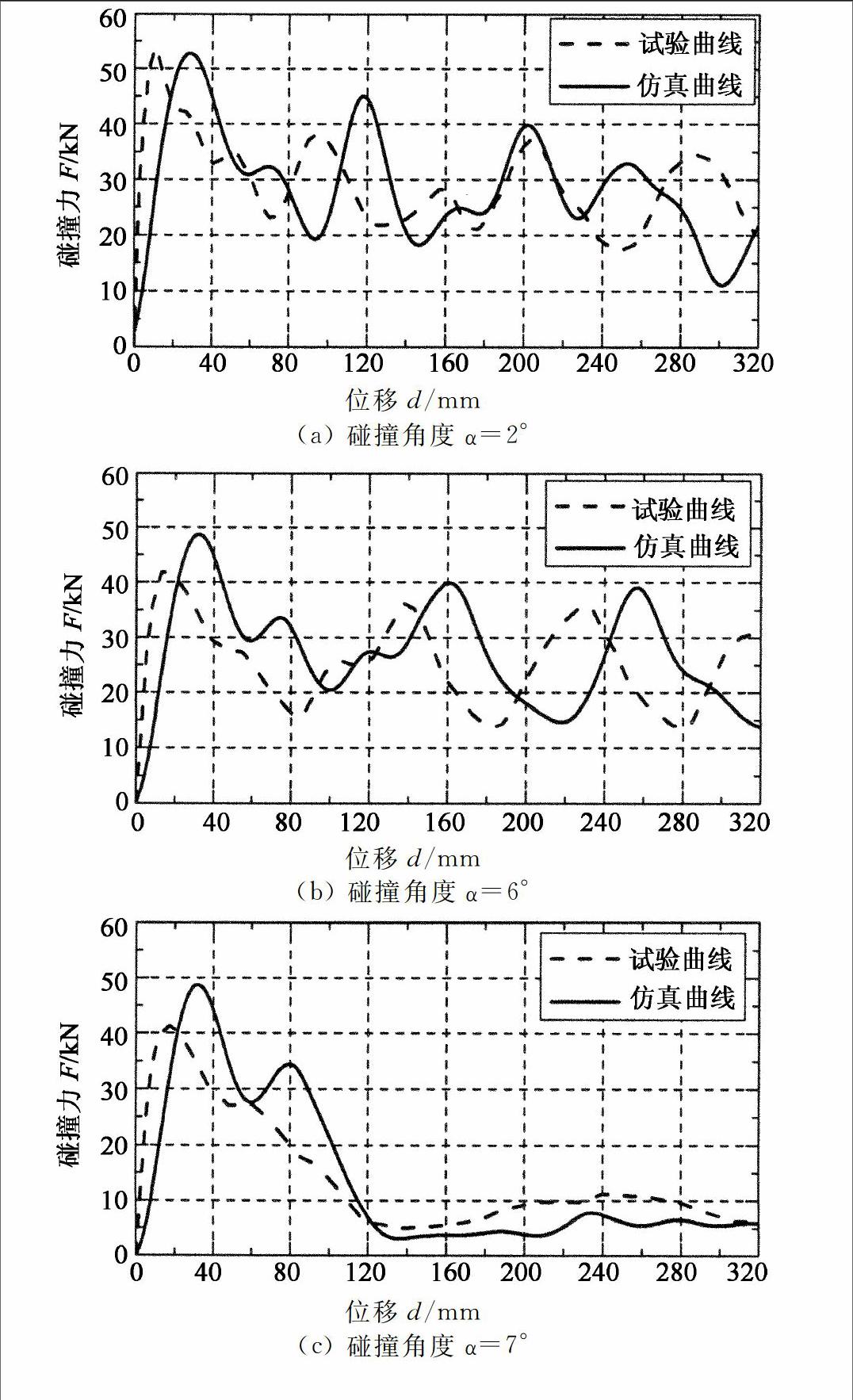
图2和图3分别为无填充薄壁梁在几个典型角度斜向碰撞下的力位移响应曲线和在不同角度下斜向碰撞的平均碰撞力。从图2和图3可以看出,波形趋势与文献[19]中的结果具有一致性,同时注意到初始峰值比文献结果要高一些,然而对表征本文主要研究的斜向载荷下的平均碰撞力和文献吻合得很好,因而验证本模型达到了应有的精度,可以用于后续的分析中。图4对比了碰撞角度为5°时,泡沫铝填充薄壁梁准静态压缩的有限元仿真和试验结果。从变形模式来看,有限元仿真结果与文献试验结果符合很好。同时,表4对比了碰撞角度分别为5°,15°和30°时的初始峰值力和平均碰撞力,也从另一方面表明了模型的有效性。
位移d/mm(a) 碰撞角度α=2°
位移d/mm(b) 碰撞角度α=6°
位移d/mm(c) 碰撞角度α=7°
位移d/mm(d) 碰撞角度α=11°
图2不同碰撞角度时薄壁梁碰撞力位移曲线
Fig。2Impact forcedisplacement
curve in different angles
碰撞角度α/(°)
图3薄壁梁平均碰撞力碰撞角度关系
Fig。3 Relationship between average
impact force and angle
图4泡沫铝填充薄壁梁斜向加载变形模式对比
Fig。4Comparison of oblique load deformation modes
表4不同碰撞角度时的峰值力和碰撞力
Tab。4Peak force and impact force of different
impact angleskN
5°
15°
30°
初始峰
值力
平均碰
撞力
初始峰
值力
平均碰
撞力
初始峰
值力
平均碰
撞力
本文结果
66。39
25。96
35。82
21。07
22。28
15。64
试验结果
66。52
27。58
36。49
20。05
22。32
15。57
相对误差/%
1。9
5。8
1。8
4。1
1。8
4。5
2参数研究
在基准模型基础上,以平均碰撞力为评价指标,研究薄壁梁壁厚、薄壁梁长宽比和泡沫铝密度对泡沫铝填充薄壁梁在斜向载荷下碰撞吸能特性的影响。平均碰撞力取薄壁梁末端节点位移为240 mm。为方便起见,薄壁梁长度不变,仅改变横截面宽度以表示不同的长宽比。各参数取值如表5所示。
表5泡沫铝填充薄壁梁研究参数及其取值
Tab。5Study parameters and values
泡沫铝密度
/(kg·m-3)
横截面宽度
/mm
长宽比
壁厚
/mm
170
70
6。86
1。3
250
75
6。40
1。5
340
80
6。00
1。7
420
85
5。65
1。9
510
90
5。33
-
2。1泡沫铝密度的影响
基于基准模型,对不同密度泡沫铝填充薄壁梁结构的斜向碰撞进行研究。图5比较了不同密度泡
沫铝填充薄壁梁和无填充薄壁梁斜向碰撞下平均碰撞力碰撞角度的关系。随着角度的增加,薄壁管会从叠缩变形过渡到弯曲变形,首次发生弯曲变形的角度称为临界角度。由图5可知,泡沫铝填充薄壁梁在斜向碰撞载荷下,其发生弯折的临界角度αc小于无填充薄壁梁临界角度(αc=7°),同时泡沫铝密度对临界角度的影响也很明显。另一方面,弯折情况下泡沫铝填充薄壁梁的平均碰撞力明显高于无填充薄壁梁,甚至当泡沫铝密度较大时和无填充薄壁梁轴向压溃时平均碰撞力相当,因此,泡沫铝填充薄壁梁在大斜向碰撞角度下具有良好的吸能特性。图6为不同密度泡沫铝填充薄壁梁发生弯折时,平均碰撞
碰撞角度α/(°)
图5不同密度薄壁梁平均碰撞力碰撞角度关系
Fig。5Comparison of average impact
force and angle of different foam density
力和斜向碰撞角度的关系。可以看出,不同泡沫铝密度下,平均碰撞力均随着碰撞角度的增加而减小,其关系可由下式拟合:
Fmean=a+b×e-cα。(2)
式中:a,b,c都是与泡沫铝密度成正相关的常数,泡沫铝密度越大,相应的平均碰撞力也越大,表明其吸能能力越大。拟合得到不同泡沫铝密度的参数值见表6。
碰撞角度α/(°)
图6不同密度薄壁梁发生弯折时
平均碰撞力碰撞角度拟合曲线
Fig。6Fitting curve of the average impact force
and the impact angle under different density
表6曲线拟合参数值
Tab。6Fitting Curve parameters
ρ/(kg·m-3)
a/kN
b/kN
c/(°)-1
170
5。792 3
15。940 2
0。076 7
250
8。079 2
18。191 8
0。111 0
340
10。545 2
20。909 4
0。147 5
420
12。120 2
25。883 4
0。174 8
510
14。722 0
26。161 6
0。180 8
2。2 宽度(长宽比)的影响
在基准模型基础上,研究泡沫铝填充薄壁梁截面宽度(长宽比)对斜向碰撞吸能的影响。横截面宽度w分别为70,75,80,85,90 mm,代表长宽比分别为6。86,6。40,6。00,5。65,5。33。图7为不同横截面宽度(长宽比)时,泡沫铝填充薄壁梁和无填充薄壁梁斜向碰撞下平均碰撞力碰撞角度的关系。结果表明,泡沫铝填充薄壁梁在斜向碰撞下吸能整体明显高于无填充薄壁梁。由于较早地发生弯折,在小碰撞角度情况下泡沫铝填充薄壁梁优势不明显,碰撞角度越大其吸能优势越明显。从图中可以看出,随着横截面宽度的增加,无填充薄壁梁弯折临界角从6°增大到9°,而泡沫铝填充薄壁梁弯折临界角度则没有明显改变。
如图8所示,在基准模型上,如果仅改变截面宽度(长宽比),平均碰撞力可表示为长宽比和碰撞角度的函数:
Fmean=(468。3+1 433。1e-0。3α)(wL)2。(3)
碰撞角度α/(°)(a) 泡沫铝填充薄壁梁
碰撞角度α/(°) (b) 无填充薄壁梁
图7不同宽度时薄壁梁平均碰撞力对比
Fig。7Comparison of average impact
force of different breadth
碰撞角度α/(°)
图8不同宽度时薄壁梁弯折时平均
碰撞力碰撞角度拟合曲线
Fig。8Fitting curve of the average impact force
and the impact angle of different breadth
2。3壁厚的影响
在基准模型基础上,研究泡沫铝填充薄壁梁壁厚对斜向碰撞的影响。图9比较了不同壁厚泡沫铝填充薄壁梁和无填充薄壁梁斜向碰撞下平均碰撞力碰撞角度的关系。无填充薄壁梁弯折临界角保持不变,与壁厚无关;壁厚对泡沫铝填充薄壁梁弯折临界角有明显的影响,且壁厚越厚弯折临界角越大。
碰撞角度/(°) (a) 泡沫铝填充薄壁梁
碰撞角度/(°) (b) 无填充薄壁梁
图9不同壁厚时薄壁梁平均碰撞力对比
Fig。9Comparison of average impact
force under different wall thickness
图10为不同碰撞角度下,泡沫铝填充薄壁梁和无填充薄壁梁平均碰撞力的比值。在大碰撞角度时的弯折吸能和小碰撞角度时的轴向吸能,泡沫铝填充薄壁梁都高于无填充薄壁梁,弯折时泡沫铝填充薄壁梁平均碰撞力约是无填充薄壁梁的1。5倍。但是填充泡沫铝薄壁梁临界角小于无填充薄壁梁,当碰撞角度介于泡沫铝填充薄壁梁临界角和无填充薄壁梁临界角之间时,泡沫铝填充薄壁梁吸能小于无填充薄壁梁。
碰撞角度/(°)
图10不同壁厚时薄壁梁平均碰撞力比值
Fig。10Ratio of the average impact
force under different wall thickness
图11为不同壁厚泡沫铝填充薄壁梁在弯折时不同碰撞角度下的平均碰撞力,平均碰撞力与碰撞角度及壁厚之间存在如下关系:
Fmean=6。49t1。5+12。85t2e-0。146tα。(4)
碰撞角度/(°)
图11不同壁厚薄壁梁在弯折时
平均碰撞力碰撞角度拟合曲线
Fig。11Fitting curve of the average impact force
and the impact angle under different wall thickness
3结论
本文研究了泡沫铝填充薄壁梁在不同角度斜向碰撞时的吸能特性。采用有限元仿真技术研究了不同泡沫铝密度、长宽比和壁厚的泡沫铝填充薄壁梁在不同角度斜向碰撞时的平均碰撞力,通过和无填充薄壁梁对比发现泡沫铝填充薄壁梁能明显提高吸能量。本文定量地给出了泡沫铝填充薄壁梁在不同斜向碰撞角度下平均碰撞力和泡沫铝密度、长宽比和壁厚的公式。研究结果表明:
1)随着碰撞角度的增加,泡沫铝填充薄壁梁吸能量减小。在临界角附近泡沫铝填充薄壁梁吸能与无填充薄壁梁相当或更小,在大碰撞角度下泡沫铝填充薄壁梁吸能远高于无填充薄壁梁。
2)平均碰撞力随着泡沫铝密度的增加而增加,而且是碰撞角度的指数函数,各系数正相关于泡沫铝密度。不同长宽比泡沫铝填充薄壁梁斜向碰撞平均碰撞力和碰撞角度满足同一个指数关系,各系数反比于长宽比平方。不同壁厚泡沫铝填充薄壁梁斜向碰撞平均碰撞力和碰撞角度是指数关系,各系数正比于壁厚的指数幂。
3)泡沫铝填充薄壁梁弯折临界角小于无填充薄壁梁,且随着泡沫铝密度增加薄壁梁弯折临界角显著减小;长宽比对泡沫铝填充薄壁梁弯折临界角没有明显影响,但对无填充薄壁梁弯折临界角影响明显,壁厚则与之相反。
同时本文仅以平均碰撞力为耐撞性评价指标,未全面考虑初始峰值力和结构质量的影响,具有一定的局限性。
参考文献
[1]BANHART J。 Manufacture, characterization and application of cellular metals and metal foams\[J\]。Progress in Materials Science, 2001, 46(6): 559-632。
[2]张维刚,黄栋。汽车薄壁梁斜向碰撞性能仿真研究\[J\]。 汽车工程,2010,32(6):515-518。
ZHANG Weigang, HUANG Dong。 Simulation study of automatic thinwalled beam crashworthiness under oblique impact loading \[J\]。Automotive Engineering, 2010, 32(6): 515-518。(In Chinese)
[3]孟志强,何涛,尹望吾,等。六角弹簧管汽车碰撞吸能装置的效能研究\[J\]。湖南大学学报: 自然科学版,2011, 38(11):43-46。
MENG Zhiqiang, HE Tao, YIN Wangwu, et al。 Research on the performances of hexagonal spring tube energyabsorbing device for car crash\[J\]。Journal of Hunan University: Natural Sciences, 2011, 38(11): 43-46。 (In Chinese)
[4]亓昌,董方亮,杨姝,等。锥形多胞薄壁梁斜向碰撞吸能特性仿真研究\[J\]。振动与冲击,2012,31(24):102-107。
QI Chang, DONG Fangliang, YANG Shu, et al。 Energyabsorbing characteristics of a tapered multicell thinwalled tube under oblique impact\[J\]。 Journal of Vibration and Shock, 2012, 31(24):102-107。(In Chinese)
[5]HAN D C, PARK S H。 Collapse behavior of square thinwalled columns subjected to oblique loads\[J\]。 Thinwalled Structures, 1999, 35(3):167-184。
[6]NAGEL G M, THAMBIRATNAM D P。 Computer simulation and energy absorption of tapered thinwalled rectangular tubes \[J\]。 ThinWalled Structures, 2005,43(8):1225-1242。
[7]THORNTON P H。 Energy absorption by foam filled structures\[R\]。 Detroit:SAE,1980。
[8]赵广宁,王社锋,赵洪伦。泡沫铝填充薄壁圆管吸能特性优化\[J\]。计算机辅助工程,2009,18(4):62-66。
ZHAO Guangning, WANG Shefeng, ZHAO Honglun。 Optimization on energy absorption performance of thinwalled pipe filled with aluminum foam\[J\]。Computer Aided Engineering, 2009,18(4):62-66。(In Chinese)
[9]徐雅晨,凤仪,汤靖婧,等。 泡沫铝填充薄壁铝合金圆管轴向压缩性能的数值模拟\[J\]。稀有金属材料与工程,2011,40(5):875-879。
XU Yachen, FENG Yi, TANG Jingjing, et al。 Numerical simulation of vertical compressing experiments of thinwalled cylindrical aluminum alloy tubes filled with aluminum foam\[J\]。Rare Metal Materials and Engineering, 2011,40(5):875-879。(In Chinese)
[10]HANSSEN A G, LANGSETH M, HOPPERSTAD O S。 Static and dynamic crushing of circular aluminum extrusions with aluminum foam filled\[J\]。International Journal of Impact Engineering, 2000,24(5):475-507。
[11]HANSSEN A G, HOPPERSTAD O S, LANGSETH M,et al。 Validation of constitutive models applicable to aluminum foam\[J\]。 International Journal of Mechanical Sciences, 2002, 44(2):359-406。
[12]谢中友,虞吉林,李剑荣。泡沫铝合金填充圆管三点弯曲实验研究\[J\]。实验力学,2007,22(2):104-110。
XIE Zhongyou, YU Jilin, LI Jianrong。 An experimental study on threepoint bending of aluminum alloy foamfilled cylindrical aluminum alloy pipe\[J\]。Journal of Experimental Mechanics,2007,22(2):104-110。(In Chinese)
[13]YANG S, QI C。 Multiobjective optimization for empty and foamfilled square columns under oblique impact loading \[J\]。 International Journal of Impact Engineering, 2013, 54(4):177-191。
[14]SANTOSA S P, WIERZBICKI T, HANSSEN A G, et al。 Experimental and numerical studies of foamfilled sections \[J\]。International Journal of Impact Engineering, 2000, 24(5):509-534。
[15]AHMAD Z, THAMBIRATNAM D P, TAN A C。 Dynamic energy absorption characteristics of foamfilled conical tubes under oblique impact loading\[J\]。International Journal of Impact Engineering,2010,37(5):475-488。
[16]HANSSEN A G, LANGSETH M, HOPPERSTAD O S。 Static and dynamic crushing of square aluminum extrusions with aluminum foam filler\[J\]。International Journal of Impact Engineering, 2000, 24(4):347-383。
[17]HOU S, LI Q, LONG S, et al。 Crashworthiness design for foam filled thinwall structures \[J\]。Materials & Design, 2009, 30(6):2024-2032。
[18]GIBSON L J, ASHBY M F。 Cellular solids: structure and properties \[M\]。Cambridge: Cambridge University Press, 1999:152-205。
[19]REYES A, HOPPERSTAD O S, LANGSETH M。 Aluminum foamfilled extrusions subjected to oblique loading: experimental and numerical study \[J\]。International Journal of Solids and Structures, 2004, 41(5):1645-1675。
[20]REID J D。 Crashworthiness of automotive steel midrails: Thickness and material sensitivity \[J\]。Thinwalled Structures, 1996, 26(2):83-103。
