不规则波诱发港湾共振条件下的低频长波实验研究

高俊亮，郑振钧，马小舟，董国海

(1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212100；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁，大连 116024)

海洋中的低频波浪是指波周期在25～300 s、波长在100 m～10 km范围内的波浪，它是近岸水域的波浪场中一种主要的波浪形式。近岸低频波浪产生的机理很多，如大气压力扰动[1]、地震诱发的海啸[2-3]、滑坡产生的冲击波[4]以及在大陆架上传播的边缘波[5]。但是，低频波浪产生的最为常见的机理为风浪或涌浪的非线性相互作用[7]。

港内水体运动的本征周期一般在数十秒至数百秒，而周期仅为十几秒的短波如风浪和涌浪很难直接诱发港湾共振。低频波浪的周期较长，更有可能接近港口的本征周期，诱发港内水体的长周期振荡，使得港口无法进行正常的货物装卸[8-9]。特别是当水体振荡周期也与港内系泊船运动周期接近时，会导致港内系泊船体的大幅度的晃动，造成系泊船和系泊设施的破坏。

Mei等[7]、Wu等[10]通过理论和实验方法研究了入射短波对于港内低频波浪的影响。这些研究发现约束于短波波群的锁相低频波浪和短波波群破碎产生的自由低频波浪可以诱发港内发生港池共振现象。通过对某些港口(如夏威夷的Barbers Point港[11]、意大利的Marina di Carrarra港[12]、西班牙的Ferrol港[13])的实地观测，也都能够发现外海的风浪或涌浪与港内的低频波浪之间存在很强的相关性。

因为港内低频波浪对港口码头作业的影响非常明显，在进行港口设计和港口管理时应对其以充分的考虑。尽管对外海短周期波浪的观测较为常见，对港内低频波浪进行直接观测还较少。因此，一些学者通过不同的方法研究了外海不规则波浪要素和近岸低频波要素之间的关系。Sand[14]通过理论推导以及与实测波浪资料的比较，证明了由波群诱发的二阶低频波能谱可以通过不规则短波能谱进行定量的计算。Nelson等[15]对澳大利亚的Jervis海湾内的某一个波浪测点和外海的某一波浪测点的实测数据进行分析，探讨了通过外海不规则短波推求近岸低频波浪的可能性。通过理论推导和现场测量，Bowers[6]定量地研究了位于中等水深的港口口门附近处低频波要素与外海不规则短波要素的关系。Zheng等[16]结合FUNWAVE-TVD模型和和人工神经网络建立了港内波高的快速估计方法，可以通过外海不规则短波要素推求港内总波高和低频波高。

现有的研究工作集中于对低频波浪的有效波高的推求，而对于通过外海不规则短波波浪要素推求低频波浪平均周期的可能性研究得比较少。然而，低频波浪平均周期与港湾共振和系泊船共振密切相关，有重要的工程意义。因此，本文通过物理模型实验，研究了通过外海波浪要素(包括有效波高、谱峰周期、波群周期)来推求一维狭长形港口内低频长波的波浪要素(包括有效波高和平均周期)的方法。研究的推求方法有2种，分别为半理论半经验公式和人工神经网络模型。

1 实验布置

本文的物理模型实验是在“大连新机场沿岸商务区填海工程(一期)A区护岸整体模型试验”[17]的基础上进行的。该实验在大连理工大学海岸和近海工程国家重点实验室多功能综合水池中开展，实验平面布局见图1。水池有效使用尺寸为34 m×55 m，最大工作水深0.7 m，配有实验室自制的不规则波造波机(0.4 m×70块)。实验的单向不规则波是基于标准JONSWAP谱生成的。

由于本文的研究目的与“大连新机场沿岸商务区填海工程(一期)A区护岸整体模型试验”的实验目的并不相同，所以实验中使用的波况并非严格地按照实际波况来进行设计。狭长形矩形港口(见图1的长度为3.5 m，宽度为0.5 m)。港口口门无任何掩护，港内的地形被制作成水平面。在港口的底端布置有2#浪高仪，在外海处布置有1#浪高仪。1#浪高仪位置处的水底高程要比港内的底面高程低3.1 cm。

图1 含有狭长型矩形港口的实验平面

实验中考虑了2个水位，分别称为低水位和高水位。在低水位状态下，港内的水深为12.8 cm，1#浪高仪处的水深为15.9 cm；在高水位状态下，港内的水深为15.4 cm，1#浪高仪处的水深为18.5 cm。根据港口水体共振解析解[18]，狭长型港口在低水位和高水位下的第1阶共振频率(周期)分别为0.069 7 Hz(14.35 s)和0.076 4 Hz(13.09 s)。

造波机产生的波浪均沿着x轴正方向传播。本文未考虑斜向传播的不规则波浪和多向不规则波浪的情况。在低水位状态下，实验考虑了14个工况(工况01A～工况14A)；在高水位状态下，实验包括了17个工况(工况01B～工况17B)。在各工况下，实验均重复3次，最后的实验结果为3次实验的平均值。本文所有实验中，每个浪高仪测得的波面时间序列均包括了215离散数据点，采样的时间间隔为0.02 s，样本长度为655.34 s。对所有波况下1#和2#浪高仪测得的波面时间序列进行快速傅里叶变换可以得到相应的波能谱。

2 物理模型实验结果

为了达到使用港外的不规则波波要素来推求港内低频波浪波要素的目的，首先需要计算出港外不规则波浪有效波高Hm、谱峰周期Tp和港内低频波浪的有效波高HL和平均周期TL。这4个参数中，港外不规则波浪的谱峰周期Tp可以直接通过谱分析得到。其他3个参数需要通过对波能谱进行进一步处理才可以得到。具体计算表公式分别为：

(1)

(2)

(3)

以低水位条件下实验工况02A为例进行讨论。图2、3分别展示了工况02A中1#和2#浪高仪测得的波面时间序列和对应的波能谱。可以看出，波浪传到港内后，高频能量衰减地非常明显。与港外相比，港内波面过程线的高频波动减弱，波能谱中f>0.2 Hz的高频能量可以忽略不计。港外波浪在浅水非线性作用下也会产生一定的低频能量(主要分布于0.1～0.2 Hz)，见图3(a)。当这些低频能量传入港内后，会显著地激发港口共振，并且波能主要集中港口的第1阶共振频率附近，见图3(b)虚线所注。可以看出港内低频区域的谱峰频率偏大于第1阶共振频率，这是因为港外低频能量频率分布范围(0.1～0.2 Hz)要偏大于港口的第1阶共振频率。综上所述，港口可以对短波起到非常好的遮挡效果。但是，低频长波的能量反而在共振条件下在港内得到聚集和放大。其余工况的波面过程线和波能谱与图2和图3相似，不再赘述。

由图3可知，对于1#浪高仪测得的波能谱，其主要能量均集中在f<1.0 Hz的范围内，f>1.0 Hz的范围内的波能可以忽略不计；而对于2#浪高仪测得的波能谱，其主要能量集中在f<0.2 Hz的范围内。因此对于式(1)～(3)，可以认为fhigh和flow分别取1.0 Hz和0.2 Hz是比较合理的。表1给出了低水位的14组实验(工况01A～14A)和高水位的17组实验(工况01B～17B)中1#和2#浪高仪得到的波浪要素。表1的数据作为推算方法研究的数据样本。

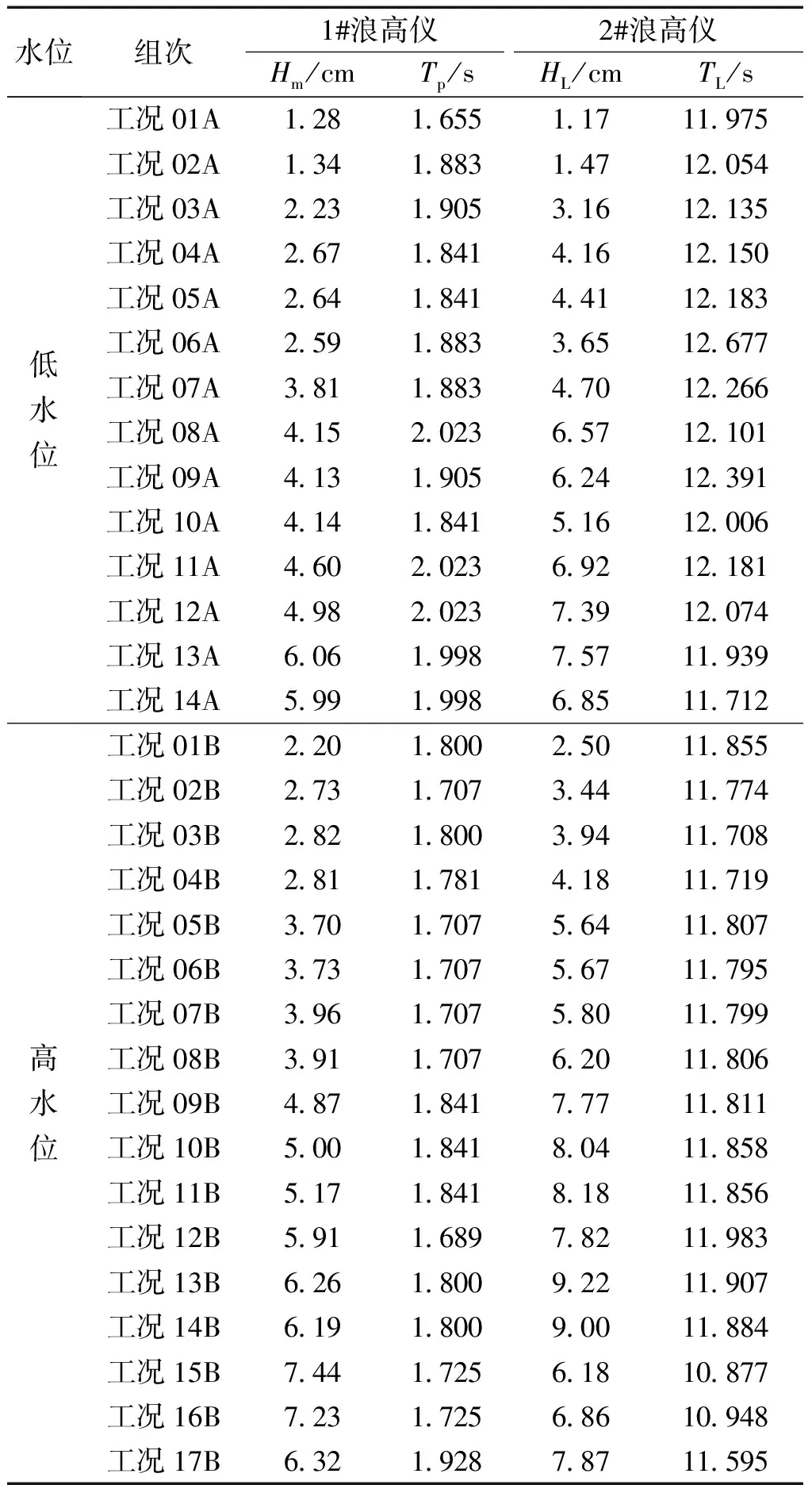
表1 各组实验中1#和2#浪高仪得到的波浪参数

3 港内低频波浪有效波高的计算

3.1 基于经验公式

参考Bowers[6]的研究成果，本文给出了使用港外不规则波要素来推求港内低频波浪有效波高的半理论半经验公式：

HL=ξ(Hm)α(Tp)β/hχ

(4)

式中：ξ、α、β和χ是待定系数;h代表1#浪高仪处的水深。需要说明的是，本文规定α、β和χ为无量纲数，而ξ的量纲是自适应的，以满足等式左右的量纲和谐。此外，该公式的指数函数形式是基于Bowers[6]的理论分析得出的，因此称之为半理论半经验公式。

通过最小二乘法，使用式(4)对表1中的数据进行拟合，可以得到待定系数ξ、α、β和χ的值。工况01A、07A、13A、01B、07B和工况13B的数据不参与拟合(不同水深下的低频长波有效波高依次增大)，专门用以检验拟合公式的效果。

图4 港内低频波有效波高的拟合值和实测值的比较(基于经验公式)

最终拟合出的参数见表2。由于样本数较少，置信区间范围较大。需要注意的是，χ的拟合值为负数，说明式(4)中水深参数并不应该在分母的位置。

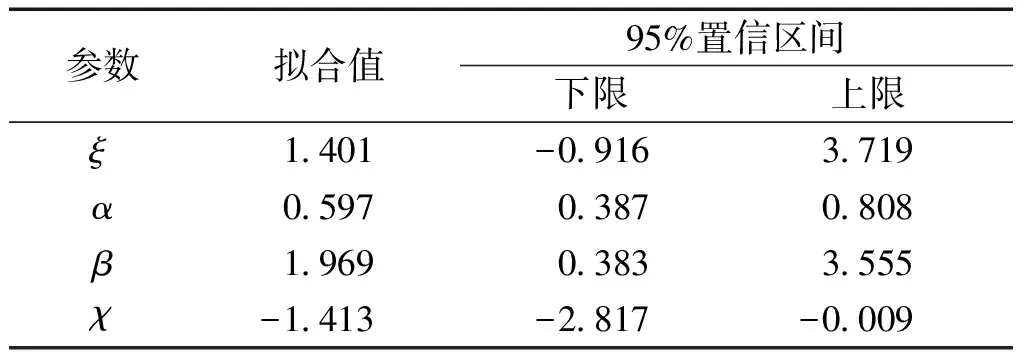
表2 经验公式(4)的拟合参数

图5显示了使用港外的不规则短波波要素拟合得到的一维矩形港内低频波浪有效波高与实测值的比较。可以发现，经验公式(4)可以很好地根据港外短波波要素来推求港内低频波浪有效波高。为了定量地说明它们之间的吻合程度，可以进一步计算出这2组数据的均方根误差和相关系数的值分别为0.008 4 m和0.894 8。

3.2 基于人工神经网络

近十几年来，人工神经网络已被广泛应用于近岸波浪条件的预测[16]。参考人类学习的方式，人工神经网络被设计用于解决多参数和非线性的复杂问题。与经验公式(4)不同，人工神经网络没有预设好的规则，因为它可以基于现有的数据去自我学习。本文的人工神经网络应用是基于Matlab的函数库完成的。

通常而言，误差后馈型神经网络包含3种结构：用于将数据传输到神经网络的输入层、用于转换数据的单个或多个的隐含层、用于输出结果的输出层。神经网络被训练好后便可以很快地处理给定的复杂问题。隐藏层层数和每层的神经网络数对计算的结果有重要影响。本文的问题并不十分复杂，样本容量也很小，因此选择了较少的隐藏层层数和每层的神经网络数，即一个[3-2-2-1]的人工神经网络结构，如图5所示。神经网络架构的选择是经验性的，本文所展现的只是其中一种可能的结果。由于实验样本较少，不开展最优网络架构的筛选工作。

图5 神经网络架构

应用神经网络的几个关键步骤简述如下：1)采用newff函数创建一个误差前馈型神经网络。2)使用train函数基于表1中的25个样本对网络进行训练。3)未参与训练的6个样本可以通过sim函数进行预测，并与实际值进行对比。

图6显示了使用港外的不规则短波波要素拟合得到的一维矩形港内低频波浪有效波高与实测值的比较。可以发现，本文建立的人工神经可以很好地根据港外不规则波要素来推求港内低频波浪有效波高。为了定量地说明它们之间的吻合程度，可以进一步计算出这2组数据的均方根误差和相关系数的值分别为0.003 0 m和0.987 9。从拟合(训练)的结果看，人工神经网络能够给出更好的均方根误差和相关系数结果。

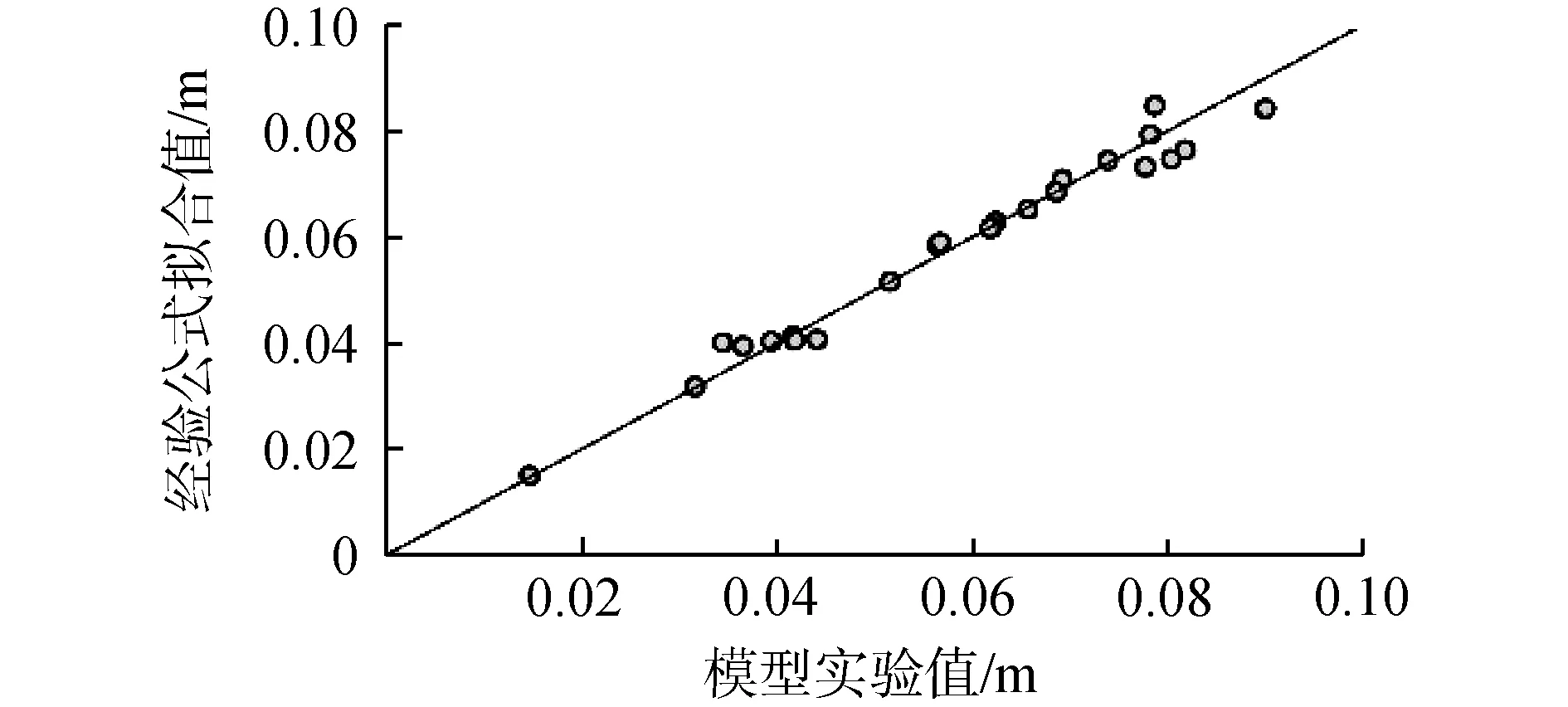
图6 港内低频波有效波高的拟合值和实测值的比较(基于人工神经网络)

经验公式和人工神经网络对未参与拟合的数据的应用结果见表3。对于经验公式，当目标波高较小时，预测波高偏大。反之，当目标波高较大时，预测波高偏小。只有在中等目标波高时才能给出较为满意的结果。对于人工神经网络模型，不管目标波高较大或者较小，都能给出令人满意的预测结果。基于本文的对比，不管是拟合(训练)阶段，还是应用阶段，人工神经网络都能给更令人满意的结果。

表3 港内低频长波有效波高验证样本的计算结果

4 港内低频波浪平均周期的计算

4.1 港内低频波浪平均周期与港外谱峰周期

根据表1中所给出的外海和港内的波浪统计参数，可以直接对外海不规则短波的谱峰周期Tp与港内低频波浪的平均周期TL进行比较(见图7)。从图7中可以发现，数据点非常分散，2组数据之间并未发现有明显的相关性。

图7 港内低频波平均周期TL与外海波浪谱峰周期Tp的对比

4.2 港内低频波浪平均周期与港外波群周期

可以使用以下3种方法来确定波群的周期：

1)时域方法：局部方差法。

该方法的原理可以参考文献[19]。波群被定义为局部方差超过样本总体方差而具有较大波能的区域。具体的计算程序

每个时间序列的总体方差为：

(5)

式中N=215表示波面时间序列的离散数据点的数量。

变动的局部方差为：

(6)

式中n从1到N-m变化，m=2Tp/Δt，I=m+1，Δt=0.02 s。

局部方差减去总体方差：

(7)

波群周期被定义为Vn的平均上跨零点周期，Tν。

2)结合的时域、频域方法。

通过对式(7)的时间序列进行FFT变换，然后在f<0.2 Hz内通过谱的零阶矩与一阶矩的比值计算得到平均波群周期，Tνm。

3)包络线方法

表4列出了使用以上3种方法计算得出的外海不规则波(即1#浪高仪测得的波面时间序列)的波群周期。从该表中可以看出，使用不同的方法计算得到的波群周期差别较大。进而，将2#浪高仪测得的港内低频波浪的平均周期TL和3种不同的方法计算得到的1#浪高仪处的不规则波浪的波群周期Tν、Tνm和Tqm进行比较(见图8)，可见数据点分布较为分散，并未观察到它们之间存在明显的关系。

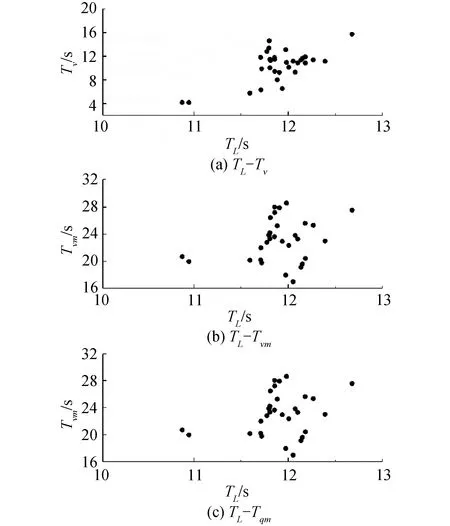
图8 港内低频波的平均周期和外海波浪波群周期的对比

表4 3种不同的方法计算得到的外海不规则波的波群周期

4.3 基于人工神经网络计算港内低频波浪平均周期

目前尚未有文献提出港内低频长波平均周期TL与港外波浪要素的关系式。同时由前面的分析知港外谱峰周期和波群周期与TL并没有明确的关系。因此，难以通过人为设定的规则来推求TL。此时更适合用人工神经网络来进行推求方法的研究。认为仍然可以基于港外不规则波浪有效波高Hm、谱峰周期Tp和水深h来推求TL。网络架构如图5所示，不过输出量由HL变为TL。工况01A、工况07A、工况13A、工况01B、工况07B、工况13B的数据不参与拟合，专门用以检验人工神经网络的效果。

图9显示了使用港外的不规则波要素拟合得到的港内低频波浪平均周期TL与实测值的比较。可以发现，本文建立的人工神经可以很好地根据港外不规则波要素来推求港内低频波浪平均周期TL。为了定量地说明它们之间的吻合程度，可以进一步计算出这2组数据的均方根误差和相关系数的值分别为0.075 5 s和0.980 9。人工神经网络对未参与拟合的数据的应用结果见表5。可以发现人工神经网络模型可以给出令人满意的预测结果。对于这种难以用显示公式描述的物理问题，人工神经网络模型的优势更加凸显。

图9 港内低频波浪平均周期的拟合值和实测值的比较(基于人工神经网络)

表5 港内低频长波平均周期验证样本的推算结果

5 结论

1)港外波浪在浅水非线性作用下也会产生一定的低频能量，当这些低频能量传入港内后，会显著地激发港口共振。港口可以对短波起到非常好的屏蔽效果。但是，港内低频长波的能量反而在共振作用下得到放大，并且波能主要集中港口的第1阶共振频率附近。

2)经验公式和人工神经网络都可以很好地利用外海不规则波的有效波高、谱峰周期和当地水深来推求港内的低频长波有效波高。在拟合(训练)阶段，人工神经网络模型对训练样本的拟合程度更好(更小的均方根误差和更大的相关系数)。在应用阶段，对于经验公式，当目标波高较小时，预测波高偏大。反之，当目标波高较大时，预测波高偏小。只有在中等目标波高时才能给出较为满意的结果。而对于人工神经网络模型，不管目标波高较大或者较小，其都能给出令人满意的预测结果。

3)通过将外海不规则波浪的谱峰周期和波群周期与港内低频长波平均周期分别进行对比，并未发现它们之间存在明显的相关性，难以提出经验公式来推算港内低频长波平均周期。采用人工神经网络模型基于外海不规则波浪要素来推求港内低频波浪平均周期。可以发现人工神经网络模型仍然可以给出令人满意的预测结果。对于这种规律不明确的物理问题，具备自我学习能力的人工神经网络模型的优势更加明显。

注意，上述结论只是对本文物理模型实验结果的一种合理的解释。